2.7: Find Multiples and Factors (Part 1)
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Identify multiples of numbers
- Use common divisibility tests
- Find all the factors of a number
- Identify prime and composite numbers
Before you get started, take this readiness quiz.
- Which of the following numbers are counting numbers (natural numbers)?
- Find the sum of
Identify Multiples of Numbers
Annie is counting the shoes in her closet. The shoes are matched in pairs, so she doesn’t have to count each one. She counts by twos:
The numbers
A multiple of a number is the product of the number and a counting number. So a multiple of
We can find the multiples of any number by continuing this process. Table
| Counting Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Multiples of 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| Multiples of 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| Multiples of 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| Multiples of 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| Multiples of 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| Multiples of 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| Multiples of 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| Multiples of 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
A number is a multiple of
Recognizing the patterns for multiples of
Figure

Figure
The last digit of each highlighted number in Figure
Determine whether each of the following is a multiple of
Solution
| Is 489 a multiple of 2? | |
| Is the last digit 0, 2, 4, 6, or 8? | No. |
| 489 is not a multiple of 2. |
| Is 3,714 a multiple of 2? | |
| Is the last digit 0, 2, 4, 6, or 8? | Yes. |
| 3,714 is a multiple of 2. |
Determine whether each number is a multiple of
- Answer a
-
yes
- Answer b
-
no
Determine whether each number is a multiple of
- Answer a
-
no
- Answer b
-
yes
Now let’s look at multiples of

Figure
All multiples of
Determine whether each of the following is a multiple of
Solution
| Is 579 a multiple of 5? | |
| Is the last digit 5 or 0? | No. |
| 579 is not a multiple of 5. |
| Is 880 a multiple of 5? | |
| Is the last digit 5 or 0? | Yes. |
| 880 is not a multiple of 5. |
Determine whether each number is a multiple of
- Answer a
-
yes
- Answer b
-
no
Determine whether each number is a multiple of
- Answer a
-
no
- Answer b
-
yes
Figure

Figure
Determine whether each of the following is a multiple of
Solution
| Is 425 a multiple of 10? | |
| Is the last digit zero? | No. |
| 425 is not a multiple of 10. |
| Is 350 a multiple of 10? | |
| Is the last digit zero? | Yes. |
| 350 is a multiple of 10. |
Determine whether each number is a multiple of
- Answer a
-
no
- Answer b
-
yes
Determine whether each number is a multiple of
- Answer a
-
yes
- Answer b
-
no
Figure

Figure
Unlike the other patterns we’ve examined so far, this pattern does not involve the last digit. The pattern for multiples of
| Multiple of 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
|---|---|---|---|---|---|---|---|---|
| Sum of digits | 3 | 6 | 9 |
1 + 2 3 |
1 + 5 6 |
1 + 8 9 |
2 + 1 3 |
2 + 4 6 |
Consider the number
Determine whether each of the given numbers is a multiple of
Solution
- Is
| Find the sum of the digits. | 6 + 4 + 5 = 15 |
| Is 15 a multiple of 3? | Yes. |
| If we're not sure, we could add its digits to find out. We can check it by dividing 645 by 3. | 645 ÷ 3 |
| The quotient is 215. | 3 • 215 = 645 |
- Is
| Find the sum of the digits. | 1 + 0 + 5 + 1 + 9 = 16 |
| Is 15 a multiple of 3? | No. |
| So 10,519 is not a multiple of 3 either.. | 645 ÷ 3 |
| We can check this by dividing by 10,519 by 3. | 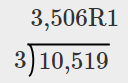 |
When we divide
Determine whether each number is a multiple of
- Answer a
-
yes
- Answer b
-
no
Determine whether each number is a multiple of
- Answer a
-
no
- Answer b
-
yes
Look back at the charts where you highlighted the multiples of
Use Common Divisibility Tests
Another way to say that
If a number
Since multiplication and division are inverse operations, the patterns of multiples that we found can be used as divisibility tests. Table
| A number is divisible by | |
|---|---|
| 2 | if the last digit is 0, 2, 4, 6, or 8 |
| 3 | if the sum of the digits is divisible by 3 |
| 5 | if the last digit is 5 or 0 |
| 6 | if divisible by both 2 and 3 |
| 10 | if the last digit is 0 |
Determine whether
Solution
Table
| Divisible by…? | Test | Divisible? | Check |
|---|---|---|---|
| 2 | Is last digit 0, 2, 4, 6, or 8? | yes | 1290 ÷ 2 = 645 |
| 3 |
Is sum of digits divisible by 3? 1 + 2 + 9 + 0 = 12 |
yes | 1290 ÷ 3 = 430 |
| 5 | Is last digit 5 or 0? | yes | 1290 ÷ 5 = 258 |
| 10 | Is last digit 0? | yes | 1290 ÷ 10 = 129 |
Thus,
Determine whether the given number is divisible by
- Answer
-
Divisible by
Determine whether the given number is divisible by
- Answer
-
Divisible by
Determine whether
Solution
Table
| Divisible by…? | Test | Divisible? | Check |
|---|---|---|---|
| 2 | Is last digit 0, 2, 4, 6, or 8? | no | 5625 ÷ 2 = 2812.5 |
| 3 |
Is sum of digits divisible by 3? 5 + 6 + 2 + 5 = 18 |
yes | 5625 ÷ 3 = 1875 |
| 5 | Is last digit 5 or 0? | yes | 5625 ÷ 5 = 1125 |
| 10 | Is last digit 0? | no | 5625 ÷ 10 = 562.5 |
Thus,
Determine whether the given number is divisible by
- Answer
-
Divisible by
Determine whether the given number is divisible by
- Answer
-
Divisible by
Find All the Factors of a Number
There are often several ways to talk about the same idea. So far, we’ve seen that if
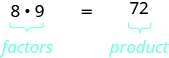
If
In algebra, it can be useful to determine all of the factors of a number. This is called factoring a number, and it can help us solve many kinds of problems.
For example, suppose a choreographer is planning a dance for a ballet recital. There are 24 dancers, and for a certain scene, the choreographer wants to arrange the dancers in groups of equal sizes on stage.
In how many ways can the dancers be put into groups of equal size? Answering this question is the same as identifying the factors of
| Number of Groups | Dancers per Group | Total Dancers |
|---|---|---|
| 1 | 24 | 1 • 24 = 24 |
| 2 | 12 | 2 • 12= 24 |
| 3 | 8 | 3 • 8= 24 |
| 4 | 6 | 4 • 6= 24 |
| 6 | 4 | 6 • 4= 24 |
| 8 | 3 | 8 • 3= 24 |
| 12 | 2 | 12 • 2= 24 |
| 24 | 1 | 24 • 1= 24 |
What patterns do you see in Table
You may notice another pattern if you look carefully at the first two columns. These two columns contain the exact same set of numbers—but in reverse order. They are mirrors of one another, and in fact, both columns list all of the factors of
We can find all the factors of any counting number by systematically dividing the number by each counting number, starting with
Step 1. Divide the number by each of the counting numbers, in order, until the quotient is smaller than the divisor.
- If the quotient is a counting number, the divisor and quotient are a pair of factors.
- If the quotient is not a counting number, the divisor is not a factor.
Step 2. List all the factor pairs.
Step 3. Write all the factors in order from smallest to largest.
Find all the factors of
Solution
Divide
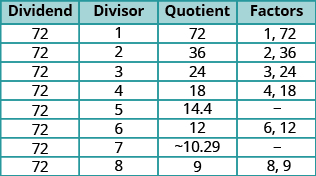
The next line would have a divisor of
Find all the factors of the given number:
- Answer
-
Find all the factors of the given number:
- Answer
-
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


