9.3: Solve Money Applications
- Page ID
- 5006
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Solve coin word problems
- Solve ticket and stamp word problems
Before you get started, take this readiness quiz.
- Multiply: 14(0.25). If you missed this problem, review Example 5.3.5.
- Simplify: 100(0.2 + 0.05n). If you missed this problem, review Example 7.4.6.
- Solve: 0.25x + 0.10(x + 4) = 2.5 If you missed this problem, review Example 8.6.8.
Solve Coin Word Problems
Imagine taking a handful of coins from your pocket or purse and placing them on your desk. How would you determine the value of that pile of coins?
If you can form a step-by-step plan for finding the total value of the coins, it will help you as you begin solving coin word problems.
One way to bring some order to the mess of coins would be to separate the coins into stacks according to their value. Quarters would go with quarters, dimes with dimes, nickels with nickels, and so on. To get the total value of all the coins, you would add the total value of each pile.

Figure \(\PageIndex{1}\) - To determine the total value of a stack of nickels, multiply the number of nickels times the value of one nickel.(Credit: Darren Hester via ppdigital)
How would you determine the value of each pile? Think about the dime pile—how much is it worth? If you count the number of dimes, you'll know how many you have—the number of dimes.
But this does not tell you the value of all the dimes. Say you counted 17 dimes, how much are they worth? Each dime is worth $0.10 —that is the value of one dime. To find the total value of the pile of 17 dimes, multiply 17 by $0.10 to get $1.70. This is the total value of all 17 dimes.
\[\begin{split} 17 \cdot \$0.10 &= \$ 1.70 \\ number\; \cdot value &= total\; value \end{split}\]
For coins of the same type, the total value can be found as follows:
\[number\; \cdot value = total\; value\]
where number is the number of coins, value is the value of each coin, and total value is the total value of all the coins.
You could continue this process for each type of coin, and then you would know the total value of each type of coin. To get the total value of all the coins, add the total value of each type of coin.
Let's look at a specific case. Suppose there are 14 quarters, 17 dimes, 21 nickels, and 39 pennies. We'll make a table to organize the information – the type of coin, the number of each, and the value.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| Quarters | 14 | 0.25 | 3.50 |
| Dimes | 17 | 0.10 | 1.70 |
| Nickels | 21 | 0.05 | 1.05 |
| Pennies | 39 | 0.01 | 0.39 |
| 6.64 |
The total value of all the coins is $6.64. Notice how Table \(\PageIndex{1}\) helped us organize all the information. Let's see how this method is used to solve a coin word problem.
Adalberto has $2.25 in dimes and nickels in his pocket. He has nine more nickels than dimes. How many of each type of coin does he have?
Solution
Step 1. Read the problem. Make sure you understand all the words and ideas.
- Determine the types of coins involved.
Think about the strategy we used to find the value of the handful of coins. The first thing you need is to notice what types of coins are involved. Adalberto has dimes and nickels.
- Create a table to organize the information.
- Label the columns ‘type’, ‘number’, ‘value’, ‘total value’.
- List the types of coins.
- Write in the value of each type of coin.
- Write in the total value of all the coins.
We can work this problem all in cents or in dollars. Here we will do it in dollars and put in the dollar sign ($) in the table as a reminder.
The value of a dime is $0.10 and the value of a nickel is $0.05. The total value of all the coins is $2.25.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| Dimes | 0.10 | ||
| Nickels | 0.05 | ||
| 2.25 |
Step 2. Identify what you are looking for.
- We are asked to find the number of dimes and nickels Adalberto has.
Step 3. Name what you are looking for.
- Use variable expressions to represent the number of each type of coin.
- Multiply the number times the value to get the total value of each type of coin. In this problem you cannot count each type of coin—that is what you are looking for—but you have a clue. There are nine more nickels than dimes. The number of nickels is nine more than the number of dimes.
- Let d = number of dimes.
- d + 9 = number of nickels
- Fill in the “number” column to help get everything organized.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| Dimes | d | 0.10 | |
| Nickels | d + 9 | 0.05 | |
| 2.25 |
Now we have all the information we need from the problem!
You multiply the number times the value to get the total value of each type of coin. While you do not know the actual number, you do have an expression to represent it.
And so now multiply number • value and write the results in the Total Value column.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| Dimes | d | 0.10 | 0.10d |
| Nickels | d + 9 | 0.05 | 0.05(d + 9) |
| 2.25 |
Step 4. Translate into an equation. Restate the problem in one sentence. Then translate into an equation.
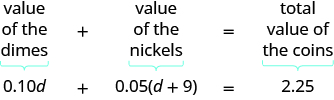
Step 5. Solve the equation using good algebra techniques.
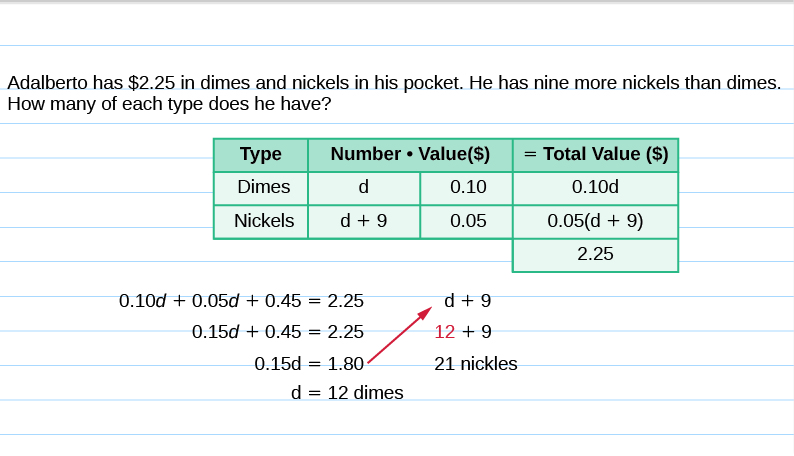
| Write the equation. | $$0.10d + 0.05(d + 9) = 2.25$$ |
| Distribute. | $$0.10d + 0.05d + 0.45 = 2.25$$ |
| Combine like terms. | $$0.15d + 0.45 = 2.25$$ |
| Subtract 0.45 from each side. | $$0.15d = 1.80$$ |
| Divide to find the number of dimes. | $$d = 12$$ |
| The number of nickels is d + 9. | $$\begin{split} d + 9& \\ \textcolor{red}{12} + 9& \\ 21& \end{split}$$ |
Step 6. Check.
\[\begin{split} 12\; dimes:\; 12(0.10) &= 1.20 \\ 21\; nickels:\; 21(0.05) &= 1.05 \\ \hline &\quad \$ 2.25\; \checkmark \end{split}\]
Step 7. Answer the question.
Adalberto has twelve dimes and twenty-one nickels.
If this were a homework exercise, our work might look like this:
Check:
\[\begin{split} 12\; dimes \quad 12(0.10) &= 1.20 \\ 21\; nickels \quad 21(0.05) &= 1.05 \\ \hline &\quad \$ 2.25 \end{split}\]
Michaela has $2.05 in dimes and nickels in her change purse. She has seven more dimes than nickels. How many coins of each type does she have?
- Answer
-
9 nickels, 16 dimes
Liliana has $2.10 in nickels and quarters in her backpack. She has 12 more nickels than quarters. How many coins of each type does she have?
- Answer
-
17 nickels, 5 quarters
Step 1. Read the problem. Make sure you understand all the words and ideas, and create a table to organize the information.
Step 2. Identify what you are looking for.
Step 3. Name what you are looking for. Choose a variable to represent that quantity.
- Use variable expressions to represent the number of each type of coin and write them in the table.
- Multiply the number times the value to get the total value of each type of coin.
Step 4. Translate into an equation. Write the equation by adding the total values of all the types of coins.
Step 5. Solve the equation using good algebra techniques.
Step 6. Check the answer in the problem and make sure it makes sense.
Step 7. Answer the question with a complete sentence.
You may find it helpful to put all the numbers into the table to make sure they check.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
Maria has $2.43 in quarters and pennies in her wallet. She has twice as many pennies as quarters. How many coins of each type does she have?
Solution
Step 1. Read the problem.
- Determine the types of coins involved. We know that Maria has quarters and pennies.
- Create a table to organize the information.
- Label the columns type, number, value, total value.
- List the types of coins.
- Write in the value of each type of coin.
- Write in the total value of all the coins.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| Quarters | 0.25 | ||
| Pennies | 0.01 | ||
| 2.43 |
Step 2. Identify what you are looking for.
- We are looking for the number of quarters and pennies.
Step 3. Name: Represent the number of quarters and pennies using variables.
- We know Maria has twice as many pennies as quarters. The number of pennies is defined in terms of quarters.
- Let q represent the number of quarters. Then the number of pennies is 2q.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| Quarters | q | 0.25 | |
| Pennies | 2q | 0.01 | |
| 2.43 |
Multiply the ‘number’ and the ‘value’ to get the ‘total value’ of each type of coin.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| Quarters | q | 0.25 | 0.25q |
| Pennies | 2q | 0.01 | 0.01(2q) |
| 2.43 |
Step 4. Translate. Write the equation by adding the 'total value’ of all the types of coins.
Step 5. Solve the equation.
| Write the equation. | $$0.25q + 0.01(2q) = 2.43$$ |
| Multiply. | $$0.25q + 0.02q = 2.43$$ |
| Combine like terms. | $$0.27q = 2.43$$ |
| Divide by 0.27. | $$q = 9\; quarters$$ |
| The number of pennies is 2q. | $$\begin{split} &2q \\ &2\; \cdot\; \textcolor{red}{9} \\ &18\; pennies \end{split}$$ |
Step 6. Check the answer in the problem. Maria has 9 quarters and 18 pennies. Does this make $2.43?
\[\begin{split} 9\; quarters \quad 9(0.25) &= 2.25 \\ 18\; pennies \quad 18(0.01) &= 0.18 \\ \hline Total \qquad \qquad \qquad \quad &\quad \$ 2.43\; \checkmark \end{split}\]
Step 7. Answer the question. Maria has nine quarters and eighteen pennies.
Sumanta has $4.20 in nickels and dimes in her desk drawer. She has twice as many nickels as dimes. How many coins of each type does she have?
- Answer
-
42 nickels, 21 dimes
Alison has three times as many dimes as quarters in her purse. She has $9.35 altogether. How many coins of each type does she have?
- Answer
-
51 dimes, 17 quarters
In the next example, we'll show only the completed table—make sure you understand how to fill it in step by step.
Danny has $2.14 worth of pennies and nickels in his piggy bank. The number of nickels is two more than ten times the number of pennies. How many nickels and how many pennies does Danny have?
Solution
| Step 1: Read the problem. | |
| Determine the types of coins involved. Create a table. | Pennies and nickels |
| Write in the value of each type of coin. |
Pennies are worth $0.01. Nickels are worth $0.05. |
| Step 2: Identify what you are looking for. | the number of pennies and nickels |
| Step 3: Name. Represent the number of each type of coin using variables. The number of nickels is defined in terms of the number of pennies, so start with pennies. | Let p = number of pennies |
| The number of nickels is two more than then times the number of pennies. | 10p + 2 = number of nickels |
Multiply the number and the value to get the total value of each type of coin.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| pennies | p | 0.01 | 0.01p |
| nickels | 10p + 2 | 0.05 | 0.05(10p + 2) |
| $2.14 |
Step 4. Translate: Write the equation by adding the total value of all the types of coins.
Step 5. Solve the equation.
| $$0.01p + 0.50p + 0.10 = 2.14$$ | |
| $$0.51p + 0.10 = 2.14$$ | |
| $$0.51p = 2.04$$ | |
| $$p = 4\; pennies$$ | |
| How many nickels? | $$10p + 2$$ |
| $$10(\textcolor{red}{4}) + 2$$ | |
| $$42\; nickels$$ |
Step 6. Check. Is the total value of 4 pennies and 42 nickels equal to $2.14?
\[\begin{split} 4(0.01) + 42(0.05) &\stackrel{?}{=} 2.14 \\ 2.14 &= 2.14\; \checkmark \end{split}\]
Step 7. Answer the question. Danny has 4 pennies and 42 nickels.
Jesse has $6.55 worth of quarters and nickels in his pocket. The number of nickels is five more than two times the number of quarters. How many nickels and how many quarters does Jesse have?
- Answer
-
41 nickels, 18 quarters
Elaine has $7.00 in dimes and nickels in her coin jar. The number of dimes that Elaine has is seven less than three times the number of nickels. How many of each coin does Elaine have?
- Answer
-
22 nickels, 59 dimes
Solve Ticket and Stamp Word Problems
The strategies we used for coin problems can be easily applied to some other kinds of problems too. Problems involving tickets or stamps are very similar to coin problems, for example. Like coins, tickets and stamps have different values; so we can organize the information in tables much like we did for coin problems.
At a school concert, the total value of tickets sold was $1,506. Student tickets sold for $6 each and adult tickets sold for $9 each. The number of adult tickets sold was 5 less than three times the number of student tickets sold. How many student tickets and how many adult tickets were sold?
Solution
Step 1: Read the problem.
- Determine the types of tickets involved. There are student tickets and adult tickets.
- Create a table to organize the information.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| Student | 6 | ||
| Adult | 9 | ||
| 1,506 |
Step 2. Identify what you are looking for. We are looking for the number of student and adult tickets.
Step 3. Name. Represent the number of each type of ticket using variables.
- We know the number of adult tickets sold was 5 less than three times the number of student tickets sold. Let s be the number of student tickets.
- Then 3s − 5 is the number of adult tickets.
- Multiply the number times the value to get the total value of each type of ticket.
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| Student | s | 6 | 6s |
| Adult | 3s - 5 | 9 | 9(9s - 5) |
| 1,506 |
Step 4. Translate: Write the equation by adding the total values of each type of ticket.
\[6s + 9(3s − 5) = 1506\]
Step 5. Solve the equation.
\[\begin{split} 6s + 27s − 45 &= 1506 \\ 33s − 45 &= 1506 \\ 33s &= 1551 \\ s &= 47\; students \end{split}\]
Substitute to find the number of adults.
\[\begin{split} 3s - 5 &= number\; of\; adults \\ 3(\textcolor{red}{47}) - 5 &= 136\; adults \end{split}\]
Step 6. Check. There were 47 student tickets at $6 each and 136 adult tickets at $9 each. Is the total value $1506? We find the total value of each type of ticket by multiplying the number of tickets times its value; we then add to get the total value of all the tickets sold.
\[\begin{split} 47 \cdot 6 &= 282 \\ 136 \cdot 9 &= 1224 \\ \hline &\quad 1506 \end{split}\]
Step 7. Answer the question. They sold 47 student tickets and 136 adult tickets.
The first day of a water polo tournament, the total value of tickets sold was $17,610. One-day passes sold for $20 and tournament passes sold for $30. The number of tournament passes sold was 37 more than the number of day passes sold. How many day passes and how many tournament passes were sold?
- Answer
-
330 day passes, 367 tournament passes
At the movie theater, the total value of tickets sold was $2,612.50. Adult tickets sold for $10 each and senior/ child tickets sold for $7.50 each. The number of senior/child tickets sold was 25 less than twice the number of adult tickets sold. How many senior/child tickets and how many adult tickets were sold?
- Answer
-
112 adult tickets, 199 senior/child tickets
Now we'll do one where we fill in the table all at once.
Monica paid $10.44 for stamps she needed to mail the invitations to her sister's baby shower. The number of 49-cent stamps was four more than twice the number of 8-cent stamps. How many 49-cent stamps and how many 8-cent stamps did Monica buy?
Solution
The type of stamps are 49-cent stamps and 8-cent stamps. Their names also give the value. “The number of 49 cent stamps was four more than twice the number of 8 cent stamps.”
Let x = number of 8-cent stamps
2x + 4 = number of 49-cent stamps
| Type | Number | Value ($) | Total Value ($) |
|---|---|---|---|
| 49-cent stamps | 2x + 4 | 0.49 | 0.49(2x + 4) |
| 8-cent stamps | x | 0.08 | 0.08x |
| 10.44 |
| Write the equation from the total values. | $$0.49(2x + 4) + 0.08x = 10.44$$ |
| Solve the equation. | $$\begin{split} 0.98x + 1.96 + 0.08x &= 10.44 \\ 1.06x + 1.96 &= 10.44 \\ 1.06x &= 8.48 \\ x &= 8 \end{split}$$ |
| Monica bought 8 eight-cent stamps. | |
| Find the number of 49-cent stamps she bought by evaluating. | 2x + 4 for x = 8.$$\begin{split} &2x + 4 \\ &2 \cdot 8 + 4 \\ &16 + 4 \\ &20 \end{split}$$ |
| Check. | $$\begin{split} 8(0.08) + 20(0.49) &\stackrel{?}{=} 10.44 \\ 0.64 + 9.80 &\stackrel{?}{=} 10.44 \\ 10.44 &= 10.44\; \checkmark \end{split}$$ |
Monica bought eight 8-cent stamps and twenty 49-cent stamps.
Eric paid $16.64 for stamps so he could mail thank you notes for his wedding gifts. The number of 49-cent stamps was eight more than twice the number of 8-cent stamps. How many 49-cent stamps and how many 8-cent stamps did Eric buy?
- Answer
-
32 at 49 cents, 12 at 8 cents
Kailee paid $14.84 for stamps. The number of 49-cent stamps was four less than three times the number of 21-cent stamps. How many 49-cent stamps and how many 21-cent stamps did Kailee buy?
- Answer
-
26 at 49 cents, 10 at 21 cents
Practice Makes Perfect
Solve Coin Word Problems
In the following exercises, solve the coin word problems.
- Jaime has $2.60 in dimes and nickels. The number of dimes is 14 more than the number of nickels. How many of each coin does he have?
- Lee has $1.75 in dimes and nickels. The number of nickels is 11 more than the number of dimes. How many of each coin does he have?
- Ngo has a collection of dimes and quarters with a total value of $3.50. The number of dimes is 7 more than the number of quarters. How many of each coin does he have?
- Connor has a collection of dimes and quarters with a total value of $6.30. The number of dimes is 14 more than the number of quarters. How many of each coin does he have?
- Carolyn has $2.55 in her purse in nickels and dimes. The number of nickels is 9 less than three times the number of dimes. Find the number of each type of coin.
- Julio has $2.75 in his pocket in nickels and dimes. The number of dimes is 10 less than twice the number of nickels. Find the number of each type of coin.
- Chi has $11.30 in dimes and quarters. The number of dimes is 3 more than three times the number of quarters. How many dimes and nickels does Chi have?
- Tyler has $9.70 in dimes and quarters. The number of quarters is 8 more than four times the number of dimes. How many of each coin does he have?
- A cash box of $1 and $5 bills is worth $45. The number of $1 bills is 3 more than the number of $5 bills. How many of each bill does it contain?
- Joe's wallet contains $1 and $5 bills worth $47. The number of $1 bills is 5 more than the number of $5 bills. How many of each bill does he have?
- In a cash drawer there is $125 in $5 and $10 bills. The number of $10 bills is twice the number of $5 bills. How many of each are in the drawer?
- John has $175 in $5 and $10 bills in his drawer. The number of $5 bills is three times the number of $10 bills. How many of each are in the drawer?
- Mukul has $3.75 in quarters, dimes and nickels in his pocket. He has five more dimes than quarters and nine more nickels than quarters. How many of each coin are in his pocket?
- Vina has $4.70 in quarters, dimes and nickels in her purse. She has eight more dimes than quarters and six more nickels than quarters. How many of each coin are in her purse?
Solve Ticket and Stamp Word Problems
In the following exercises, solve the ticket and stamp word problems.
- The play took in $550 one night. The number of $8 adult tickets was 10 less than twice the number of $5 child tickets. How many of each ticket were sold?
- If the number of $8 child tickets is seventeen less than three times the number of $12 adult tickets and the theater took in $584, how many of each ticket were sold?
- The movie theater took in $1,220 one Monday night. The number of $7 child tickets was ten more than twice the number of $9 adult tickets. How many of each were sold?
- The ball game took in $1,340 one Saturday. The number of $12 adult tickets was 15 more than twice the number of $5 child tickets. How many of each were sold?
- Julie went to the post office and bought both $0.49 stamps and $0.34 postcards for her office's bills She spent $62.60. The number of stamps was 20 more than twice the number of postcards. How many of each did she buy?
- Before he left for college out of state, Jason went to the post office and bought both $0.49 stamps and $0.34 postcards and spent $12.52. The number of stamps was 4 more than twice the number of postcards. How many of each did he buy?
- Maria spent $16.80 at the post office. She bought three times as many $0.49 stamps as $0.21 stamps. How many of each did she buy?
- Hector spent $43.40 at the post office. He bought four times as many $0.49 stamps as $0.21 stamps. How many of each did he buy?
- Hilda has $210 worth of $10 and $12 stock shares. The numbers of $10 shares is 5 more than twice the number of $12 shares. How many of each does she have?
- Mario invested $475 in $45 and $25 stock shares. The number of $25 shares was 5 less than three times the number of $45 shares. How many of each type of share did he buy?
Everyday Math
- Parent Volunteer As the treasurer of her daughter's Girl Scout troop, Laney collected money for some girls and adults to go to a 3-day camp. Each girl paid $75 and each adult paid $30. The total amount of money collected for camp was $765. If the number of girls is three times the number of adults, how many girls and how many adults paid for camp?
- Parent Volunteer Laurie was completing the treasurer's report for her son's Boy Scout troop at the end of the school year. She didn't remember how many boys had paid the $24 full-year registration fee and how many had paid a $16 partial-year fee. She knew that the number of boys who paid for a full-year was ten more than the number who paid for a partial-year. If $400 was collected for all the registrations, how many boys had paid the full-year fee and how many had paid the partial-year fee?
Writing Exercises
- Suppose you have 6 quarters, 9 dimes, and 4 pennies. Explain how you find the total value of all the coins.
- Do you find it helpful to use a table when solving coin problems? Why or why not?
- In the table used to solve coin problems, one column is labeled “number” and another column is labeled ‘“value.” What is the difference between the number and the value?
- What similarities and differences did you see between solving the coin problems and the ticket and stamp problems?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

(b) After reviewing this checklist, what will you do to become confident for all objectives?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


