4.8: Order of Operations with Fractions
- Page ID
- 24081
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Let’s begin by taking powers of fractions. Recall that
\[ a^m = \underbrace{a \cdot a \cdot ... \cdot a}_{m \text{ times}}\nonumber \]
Simplify: (−3/4)2.
Solution
By definition,
\[ \begin{aligned} \left( - \frac{3}{4} \right)^2 = \left( - \frac{3}{4} \right) \left( - \frac{3}{4} \right) ~& \textcolor{red}{ \text{ Fact: } a^2 = a \cdot a.} \\ = \frac{3 \cdot 3}{4 \cdot 4} ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply numerators and denominators.} \\ \text{ Product of even number of negative factors is positive.} \end{array}} \\ = \frac{9}{16} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Simplify:
\[ \left( - \frac{2}{5} \right)^2\nonumber \]
- Answer
-
4/25
Simplify: (−2/3)3.
Solution
By definition,
\[ \begin{aligned} \left( - \frac{2}{3}\right)^3 = \left( - \frac{2}{3} \right) \left( - \frac{2}{3} \right) \left( - \frac{2}{3} \right) ~ & \textcolor{red}{ \text{ Fact: } a^3 = a \cdot a \cdot a.} \\ = - \frac{2 \cdot 2 \cdot 2}{3 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \begin{array} ~ \text{ Multiply numerators and denominators.} \\ \text{ Product of odd number of negative factors is negative.} \end{array}} \\ = - \frac{8}{27} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Simplify:
\[ \left( - \frac{1}{6} \right)^3\nonumber \]
- Answer
-
−1/216
The last two examples reiterate a principle learned earlier.
- The product of an even number of negative factors is positive.
- The product of an odd number of negative factors is negative.
Order of Operations
For convenience, we repeat here the rules guiding order of operations.
When evaluating expressions, proceed in the following order.
- Evaluate expressions contained in grouping symbols first. If grouping symbols are nested, evaluate the expression in the innermost pair of grouping symbols first.
- Evaluate all exponents that appear in the expression.
- Perform all multiplications and divisions in the order that they appear in the expression, moving left to right.
- Perform all additions and subtractions in the order that they appear in the expression, moving left to right.
Simplify: \(- \frac{1}{2} + \frac{1}{4} \left( - \frac{1}{3} \right)\).
Solution
Multiply first, then add.
\[ \begin{aligned} - \frac{1}{2} + \frac{1}{4} \left( - \frac{1}{3} \right) = - \frac{1}{2} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Multiply: } \frac{1}{4} \left( - \frac{1}{3} \right) = - \frac{1}{12}.} \\ = - \frac{1 \cdot \textcolor{red}{6}}{2 \cdot \textcolor{red}{6}} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 12.}} \\ = - \frac{6}{12} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = - \frac{7}{12} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]
Simplify: \( - \frac{2}{3} + \frac{3}{4} \left( - \frac{1}{2} \right)\)
- Answer
-
−25/24
Simplify: \(2 \left( - \frac{1}{2} \right)^2 +4 \left( - \frac{1}{2} \right)\).
Solution
Exponents first, then multiply, then add.
\[ \begin{aligned} 2 \left( - \frac{1}{2} \right)^2 + 4 \left( - \frac{1}{2} \right) = 2 \left( \frac{1}{4} \right) + 4 \left( - \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ Exponent first: } \left( - \frac{1}{2} \right)^2 = \frac{1}{4}.} \\ = \frac{1}{2} + \left( - \frac{2}{1} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply: } 2 \left( \frac{1}{4} \right) = \frac{1}{2} \\ \text{ and } 4 \left( - \frac{1}{2} \right) = - \frac{2}{1}. \end{array}} \\ = \frac{1}{2} + \left( - \frac{2 \cdot \textcolor{red}{2}}{1 \cdot \textcolor{red}{2}} \right) ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 2.}} \\ = \frac{1}{2} + \left( - \frac{4}{2} \right) ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = - \frac{3}{2} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]
Simplify: \(3 \left( - \frac{1}{3} \right)^2 - 2 \left( - \frac{1}{3} \right)\)
- Answer
-
1
Given a = −3/4, b = 1/2, c = 1/3, and d = −1/4, evaluate the expression ab − cd.
Solution
Recall that it is good practice to prepare parentheses before substituting.
\[ ad - bc = ( ~ ) (~) - (~)(~)\nonumber \]
Substitute the given values into the algebraic expression, then simplify using order of operations.
\[ \begin{aligned} ab - cd = \left( - \frac{3}{4} \right) \left( \frac{1}{2} \right) - \left( \frac{1}{3} \right) \left( - \frac{1}{4} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Substitute: } -3/4 \text{ for } a, ~ 1/2 \text{ for } b, \\ 1/3 \text{ for } c, ~ \text{ and } -1/4 \text{ for } d. \end{array}} \\ = - \frac{3}{8} - \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply first: } \left( - \frac{3}{4} \right) \left( \frac{1}{2} \right) = - \frac{3}{8} \\ \text{ and } \left( \frac{1}{3} \right) \left( - \frac{1}{4} \right) = - \frac{1}{12}. \end{array}} \\ = - \frac{3}{8} + \frac{1}{12} ~ & \textcolor{red}{ \text{ Subtract by adding opposite.}} \\ = - \frac{3 \cdot \textcolor{red}{3}}{8 \cdot \textcolor{red}{3}} + \frac{1 \cdot \textcolor{red}{2}}{12 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions; LCD = 24.}} \\ = - \frac{9}{24} + \frac{2}{24} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = - \frac{7}{24} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]
Given a = −1/2, b = 1/3, and c = −1/5, evaluate a + bc.
- Answer
-
−17/30
Given a = −1/4 and b = 1/2, evaluate (a2 − b2) ÷ (a + b).
Solution
Recall that it is good practice to prepare parentheses before substituting.
\[ (a^2 - b^2 ) \div (a+b) - \left( (~)^2 - (~)^2 \right) \div \left( (~) + (~) \right)\nonumber \]
Substitute the given values into the algebraic expression, then evaluate exponents first.
\[ \begin{array}{l} (a^2 -b^2) \div (a+b) & = \left( \left( - \frac{1}{4} \right)^2 - \left( \frac{1}{2} \right)^2 \right) \div \left( \left( - \frac{1}{4} \right) + \left( \frac{1}{2} \right) \right) \\ ~ & = \left( \frac{1}{16} - \frac{1}{4} \right) \div \left( - \frac{1}{4} + \frac{1}{2} \right) \end{array}\nonumber \]
We must evaluate parentheses first. Inside each set of parentheses, create equivalent fractions and perform subtractions and additions next.
\[ \begin{array}{l} = \left( \frac{1}{16} - \frac{1 \cdot 4}{4 \cdot 4} \right) \div \left( - \frac{1}{4} + \frac{1 \cdot 2}{2 \cdot 2} \right) \\ = \left( \frac{1}{16} - \frac{4}{16} \right) \div \left( - \frac{1}{4} + \frac{2}{4} \right) \\ = - \frac{3}{16} \div \frac{1}{4} \end{array}\nonumber \]
Invert and multiply.
\[ \begin{aligned} = - \frac{3}{16} \cdot \frac{4}{1} \\ = - \frac{12}{16} \end{aligned}\nonumber \]
Reduce.
\[ \begin{aligned} = - \frac{12 \div 4}{16 \div 4} \\ - \frac{3}{4} \end{aligned}\nonumber \]
Note: In the last step, you could also reduce by prime factoring numerator and denominator and canceling common factors.
Give a = −1/2 and b = −1/3, evaluate ab ÷ (a + b).
- Answer
-
−1/5
Complex Fractions
When the numerator and denominator of a fraction contain fractions themselves, such an expression is called a complex fraction.
You can use the standard order of operations to simplify a complex fraction. Recall the advice when a fraction is present.
If a fractional expression is present, simplify the numerator and denominator separately, then divide.
Simplify:
\[ \frac{ - \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}}\nonumber \]
Solution
We have addition in the numerator, subtraction in the denominator. In each case, we need equivalent fractions with a common denominator.
\[ \begin{aligned} \frac{- \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}} = \frac{- \frac{1 \cdot \textcolor{red}{3}}{2 \cdot \textcolor{red}{3}} + \frac{1 \cdot \textcolor{red}{2}}{3 \cdot \textcolor{red}{2}}} ~ & \textcolor{red}{ \text{ Create equivalent fractions.}} \\ = \frac{- \frac{3}{6} + \frac{2}{6}}{ \frac{3}{4} - \frac{6}{4}} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = \frac{- \frac{1}{6}}{- \frac{3}{4}} ~ & \textcolor{red}{ \begin{array}{l} ~ \text{ Numerator: } - \frac{3}{6} + \frac{2}{6} = - \frac{1}{6}. \\ \text{ Denominator: } \frac{3}{4} - \frac{6}{4} = - \frac{3}{4}. \end{array}} \end{aligned}\nonumber \]
The last expression asks us to divide. Invert and multiply.
\[ \begin{aligned} = - \frac{1}{6} \div \left( - \frac{3}{4} \right) ~ & \textcolor{red}{ \text{ A complex fraction means divide.}} \\ = - \frac{1}{6} \cdot \left( - \frac{4}{3} \right) ~ & \textcolor{red}{ \text{ Invert and multiply.}} \end{aligned}\nonumber \]
Like signs (two negatives) give a positive product. Multiply numerators and denominators, then reduce.
\[ \begin{aligned} = \frac{4}{18} ~ & \textcolor{red}{ \begin{array}{l} \text{ Like signs yields positive answer.} \\ \text{ Multiply numerators and denominators.} \end{array}} \\ = \frac{4 \div 2}{18 \div 2} ~ & \textcolor{red}{ \text{ Divide both numerator and denominator by 2.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Alternatively, one could prime factor and cancel to reduce to lowest terms; that is,
\[ \begin{aligned} \frac{4}{18} = \frac{2 \cdot 2}{2\cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = \frac{ \cancel{2} \cdot 2}{ \cancel{2} \cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Simplify:
\[ \frac{ \frac{1}{4} - \frac{1}{3}}{ \frac{1}{4} + \frac{1}{3}}\nonumber \]
- Answer
-
−1/7
Clearing Fractions
An alternate technique for simplifying complex fractions is available.
You can clear fractions from a complex fraction using the following algorithm:
- Determine an LCD1 for the numerator.
- Determine an LCD2 for the denominator.
- Determine an LCD for both LCD1 and LCD2.
- Multiply both numerator and denominator by this “combined” LCD.
Let’s apply this technique to the complex fraction of Example 7.
Simplify:
\[ \frac{- \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}}\nonumber \]
Solution
As we saw in the solution in Example 7, common denominators of 6 and 4 were used for the numerator and denominator, respectively. Thus, a common denominator for both numerator and denominator would be 12. We begin the alternate solution technique by multiplying both numerator and denominator by 12.
\[ \begin{aligned} \frac{ - \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}} = \frac{ \textcolor{red}{12} \left( - \frac{1}{2} + \frac{1}{3} \right)}{ \textcolor{red}{12} \left( \frac{3}{4} - \frac{3}{2} \right)} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 12.}} \\ = \frac{ \textcolor{red}{12} \left( - \frac{1}{2} \right) + \textcolor{red}{12} \left( \frac{1}{3} \right)}{ \textcolor{red}{12} \left( \frac{3}{4} \right) - \textcolor{red}{12} \left( \frac{3}{2} \right)} ~ & \textcolor{red}{ \text{ Distribute the 12.}} \\ = \frac{-6+4}{9-18} ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply: } 12(-1/2)=-6,~ 12(1/2) = 4. \\ 12(3/4)=9, \text{ and } 12(3/2)=18. \end{array}} \\ = \frac{-2}{-9} ~ & \textcolor{red}{ \text{ Simplify.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Like signs yield positive.}} \end{aligned}\nonumber \]
Simplify: \( \frac{- \frac{2}{3} + \frac{1}{5}}{ \frac{4}{5} - \frac{1}{2}}\)
- Answer
-
−14/9
Application — Trapezoid
A trapezoid is a special type of quadrilateral (four-sided polygon).
A quadrilateral with one pair of parallel opposite sides is called a trapezoid.
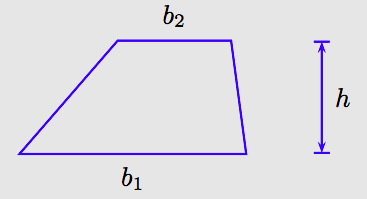
The pair of parallel sides are called the bases of the trapezoid. Their lengths are marked by the variables b1 and b2 in the figure above. The distance between the parallel bases is called the height or altitude of the trapezoid. The height is marked by the variable h in the figure above.
Mathematicians use subscripts to create new variables. Thus, b1 (“b sub 1”) and b2 (“b sub 2”) are two distinct variables, used in this case to represent the length of the bases of the trapezoid.
By drawing in a diagonal, we can divide the trapezoid into two triangles (see Figure 4.14).
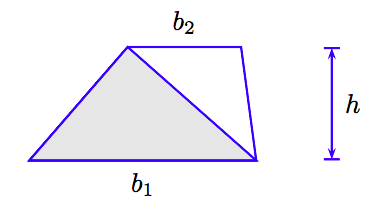
We can find the area of the trapezoid by summing the areas of the two triangles.
- The shaded triangle in Figure 4.14 has base b1 and height h. Hence, the area of the shaded triangle is (1/2)b1h.
- The unshaded triangle in Figure 4.14 has base b2 and height h. Hence, the area of the unshaded triangle is (1/2)b2h.
Summing the areas, the area of the trapezoid is
\[ \text{Area of Trapezoid} = \frac{1}{2} b_1h + \frac{1}{2} b_2h.\nonumber \]
We can use the distributive property to factor out a (1/2)h.
A trapezoid with bases b1 and b2 and height h has area
\[A = \frac{1}{2} h (b_1 + b_2).\nonumber \]
That is, to find the area, sum the bases, multiply by the height, and take one-half of the result.
Find the area of the trapezoid pictured below.
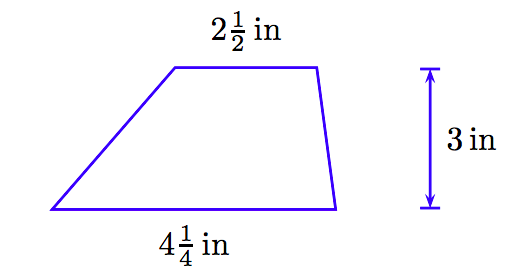
Solution
The formula for the area of a trapezoid is
\[A = \frac{1}{2} h (b_1 + b_2)\nonumber \]
Substituting the given bases and height, we get
\[A = \frac{1}{2} (3) \left( 4 \frac{1}{4} + 2 \frac{1}{2} \right).\nonumber \]
Simplify the expression inside the parentheses first. Change mixed fractions to improper fractions, make equivalent fractions with a common denominator, then add.
\[\begin{array}{c} A = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{5}{2} \right) \\ = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{5 \cdot 2}{2 \cdot 2} \right) \\ = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{10}{4} \right) \\ = \frac{1}{2} \left( \frac{3}{1} \right) \left( \frac{27}{4} \right) \end{array}\nonumber \]
Multiply numerators and denominators.
\[ = \frac{81}{8}\nonumber \]
This improper fraction is a perfectly good answer, but let’s change this result to a mixed fraction (81 divided by 8 is 10 with a remainder of 1). Thus, the area of the trapezoid is
\[A = 10 \frac{1}{8} \text{ square inches.}\nonumber \]
A trapezoid has bases measuring 6 and 15 feet, respectively. The height of the trapezoid is 5 feet. Find the area of the trapezoid.
- Answer
-
\(52 \frac{1}{2} \text{ square feet}\)
Exercises
In Exercises 1-8, simplify the expression.
1. \( \left( − \frac{7}{3} \right)^3\)
2. \( \left( \frac{1}{2} \right)^3\)
3. \( \left( \frac{5}{3} \right)^4\)
4. \( \left( − \frac{3}{5} \right)^4\)
5. \( \left( \frac{1}{2} \right)^5\)
6. \( \left( \frac{3}{4} \right)^5\)
7. \( \left( \frac{4}{3} \right)^2\)
8. \( \left( − \frac{8}{5} \right)^2\)
9. If a = 7/6, evaluate a3.
10. If e = 1/6, evaluate e3.
11. If e = −2/3, evaluate −e2.
12. If c = −1/5, evaluate −c2.
13. If b = −5/9, evaluate b2.
14. If c = 5/7, evaluate c2.
15. If b = −1/2, evaluate −b3.
16. If a = −2/9, evaluate −a3.
In Exercises 17-36, simplify the expression.
17. \( \left( − \frac{1}{2} \right) \left( \frac{1}{6} \right) − \left( \frac{7}{8} \right) \left( − \frac{7}{9} \right)\)
18. \( \left( − \frac{3}{4} \right) \left( \frac{1}{2} \right) − \left( \frac{3}{5} \right) \left( \frac{1}{4} \right)\)
19. \( \left( − \frac{9}{8} \right)^2 − \left( − \frac{3}{2} \right) \left( \frac{7}{3} \right)\)
20. \( \left( \frac{3}{2} \right)^2 − \left( \frac{7}{8} \right) \left( − \frac{1}{2} \right)\)
21. \( \left( − \frac{1}{2} \right) \left( − \frac{7}{4} \right) − \left( − \frac{1}{2} \right)^2\)
22. \( \left( \frac{1}{5} \right) \left( − \frac{9}{4} \right) − \left( \frac{7}{4} \right)^2\)
23. \(− \frac{7}{6} − \frac{1}{7} \cdot \frac{7}{9}\)
24. \( − \frac{4}{9} − \frac{8}{5} \cdot \frac{8}{9}\)
25. \( \frac{3}{4} + \frac{9}{7} \left( − \frac{7}{6} \right)\)
26. \( \frac{3}{2} + \frac{1}{4} \left( − \frac{9}{8} \right)\)
27. \( \left( − \frac{1}{3} \right)^2 + \left( \frac{7}{8} \right) \left( − \frac{1}{3} \right)\)
28. \( \left( − \frac{2}{9} \right)^2 + \left( \frac{2}{3} \right) \left( \frac{1}{2} \right)\)
29. \(\frac{5}{9} + \frac{5}{9} \cdot \frac{7}{9}\)
30. \( − \frac{1}{2} + \frac{9}{8} \cdot \frac{1}{3}\)
31. \( \left( − \frac{5}{6} \right) \left( \frac{3}{8} \right) + \left( − \frac{7}{9} \right) \left( − \frac{3}{4} \right)\)
32. \( \left( \frac{7}{4} \right) \left( \frac{6}{5} \right) + \left( − \frac{2}{5} \right) \left( \frac{8}{3} \right)\)
33. \( \frac{4}{3} − \frac{2}{9} \left( − \frac{3}{4} \right)\)
34. \(− \frac{1}{3} − \frac{1}{5} \left( − \frac{4}{3} \right)\)
35. \( \left( − \frac{5}{9} \right) \left( \frac{1}{2} \right) + \left( − \frac{1}{6} \right)^2\)
36. \( \left( \frac{1}{4} \right) \left( \frac{1}{6} \right) + \left( − \frac{5}{6} \right)^2\)
37. Given a = −5/4, b = 1/2, and c = 3/8, evaluate a + bc.
38. Given a = −3/5, b = 1/5, and c = 1/3, evaluate a + bc.
39. Given x = −1/8, y = 5/2, and z = −1/2, evaluate the expression x + yz.
40. Given x = −5/9, y = 1/4, and z = −2/3, evaluate the expression x + yz.
41. Given a = 3/4, b = 5/7, and c = 1/2, evaluate the expression a − bc.
42. Given a = 5/9, b = 2/3, and c = 2/9, evaluate the expression a − bc.
43. Given x = −3/2, y = 1/4, and z = −5/7, evaluate x2 − yz.
44. Given x = −3/2, y = −1/2, and z = 5/3, evaluate x2 − yz.
45. Given a = 6/7, b = 2/3, c = −8/9, and d = −6/7, evaluate ab + cd.
46. Given a = 4/9, b = −3/2, c = 7/3, and d = −8/9, evaluate ab + cd.
47. Given w = −1/8, x = −2/7, y = −1/2, and z = 8/7, evaluate wx − yz.
48. Given w = 2/7, x = −9/4, y = −3/4, and z = −9/2, evaluate wx − yz.
49. Given x = 3/8, y = 3/5, and z = −3/2, evaluate xy + z2.
50. Given x = −1/2, y = 7/5, and z = −3/2, evaluate xy + z2.
51. Given u = 9/7, v = 2/3, and w = −3/7, evaluate uv − w2.
52. Given u = 8/7, v = −4/3, and w = 2/3, evaluate uv − w2.
53. Given a = 7/8, b = −1/4, and c = −3/2, evaluate a2 + bc.
54. Given a = −5/8, b = 3/2, and c = −3/2, evaluate a2 + bc.
55. Given u = 1/3, v = 5/2, and w = −2/9, evaluate the expression u − vw.
56. Given u = −1/2, v = 1/4, and w = −1/4, evaluate the expression u − vw.
In Exercises 57-68, simplify the complex rational expression.
57. \(\frac{ \frac{8}{3} + \frac{7}{6}}{− \frac{9}{2} − \frac{1}{4}}\)
58. \( \frac{ \frac{7}{8} + \frac{1}{9}}{ \frac{8}{9} − \frac{1}{6}}\)
59. \( \frac{ \frac{3}{4} + \frac{4}{3}}{ \frac{1}{9} + \frac{5}{3}}\)
60. \( \frac{− \frac{9}{8} − \frac{6}{5}}{ \frac{7}{4} + \frac{1}{2}}\)
61. \( \frac{ \frac{7}{5} + \frac{5}{2}}{− \frac{1}{4} + \frac{1}{2}}\)
62. \( \frac{ \frac{5}{6} + \frac{2}{3}}{ \frac{3}{5} + \frac{2}{3}}\)
63. \( \frac{− \frac{3}{2} − \frac{2}{3}}{− \frac{7}{4} − \frac{2}{3}}\)
64. \( \frac{ \frac{8}{9} + \frac{3}{4}}{− \frac{2}{3} − \frac{1}{6}}\)
65. \( \frac{− \frac{1}{2} − \frac{4}{7}}{− \frac{5}{7} + \frac{1}{6}}\)
66. \( \frac{− \frac{3}{2} − \frac{5}{8}}{ \frac{3}{4} − \frac{1}{2}}\)
67. \(\frac{− \frac{3}{7} − \frac{1}{3}}{ \frac{1}{3} − \frac{6}{7}}\)
68. \( \frac{− \frac{5}{8} − \frac{6}{5}}{− \frac{5}{4} − \frac{3}{8}}\)
69. A trapezoid has bases measuring \(3 \frac{3}{8}\) and \(5 \frac{1}{2}\) feet, respectively. The height of the trapezoid is 7 feet. Find the area of the trapezoid.
70. A trapezoid has bases measuring \(2 \frac{1}{2}\) and \(6 \frac{7}{8}\) feet, respectively. The height of the trapezoid is 3 feet. Find the area of the trapezoid.
71. A trapezoid has bases measuring \(2 \frac{1}{4}\) and \(7 \frac{3}{8}\) feet, respectively. The height of the trapezoid is 7 feet. Find the area of the trapezoid.
72. A trapezoid has bases measuring \(3 \frac{1}{8}\) and \(6 \frac{1}{2}\) feet, respectively. The height of the trapezoid is 3 feet. Find the area of the trapezoid.
73. A trapezoid has bases measuring \(2 \frac{3}{4}\) and \(6 \frac{5}{8}\) feet, respectively. The height of the trapezoid is 3 feet. Find the area of the trapezoid.
74. A trapezoid has bases measuring \(2 \frac{1}{4}\) and \(7 \frac{1}{8}\) feet, respectively. The height of the trapezoid is 5 feet. Find the area of the trapezoid.
Answers
1. \(\frac{−343}{27}\)
3. \(\frac{625}{81}\)
5. \(\frac{1}{32}\)
7. \(\frac{16}{9}\)
9. \(\frac{343}{216}\)
11. \(\frac{−4}{9}\)
13. \(\frac{25}{81}\)
15. \(\frac{1}{8}\)
17. \(\frac{43}{72}\)
19. \(\frac{305}{64}\)
21. \(\frac{5}{8}\)
23. \(\frac{−23}{18}\)
25. \(\frac{−3}{4}\)
27. \(\frac{−13}{72}\)
29. \(\frac{80}{81}\)
31. \(\frac{13}{48}\)
33. \(\frac{3}{2}\)
35. \(\frac{−1}{4}\)
37. \(\frac{−17}{16}\)
39. \(\frac{−11}{8}\)
41. \(\frac{11}{28}\)
43. \(\frac{17}{7}\)
45. \(\frac{4}{3}\)
47. \(\frac{17}{28}\)
49. \(\frac{99}{40}\)
51. \(\frac{33}{49}\)
53. \(\frac{73}{64}\)
55. \(\frac{8}{9}\)
57. \(\frac{−46}{57}\)
59. \(\frac{75}{64}\)
61. \(\frac{78}{5}\)
63. \(\frac{26}{29}\)
65. \(\frac{45}{23}\)
67. \(\frac{16}{11}\)
69. \(31 \frac{1}{16}\)
71. \(33 \frac{11}{16}\)
73. \(14 \frac{1}{16}\)


