4.9: Solving Equations with Fractions
- Page ID
- 24084
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Undoing Subtraction
We can still add the same amount to both sides of an equation without changing the solution.
Solve for x: \(x - \frac{5}{6} = \frac{1}{3}\).
Solution
To “undo” subtracting 5/6, add 5/6 to both sides of the equation and simplify.
\[ \begin{aligned} x - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ x - \frac{5}{6} + \frac{5}{6} = \frac{1}{3} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Add } \frac{5}{6} \text{ to both sides.}} \\ x = \frac{1 \cdot 2}{3 \cdot 2} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 6.}} \\ x = \frac{2}{6} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Simplify.}} \\ x = \frac{7}{6} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]
It is perfectly acceptable to leave your answer as an improper fraction. If you desire, or if you are instructed to do so, you can change your answer to a mixed fraction (7 divided by 6 is 1 with a remainder of 1). That is \(x = 1 \frac{1}{6}\).
Checking the Solution
Substitute 7/6 for x in the original equation and simplify.
\[ \begin{aligned} x - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{7}{6} - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Substitute 7/6 for } x.} \\ \frac{2}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Subtract.}} \\ \frac{1}{3} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Reduce.}} \end{aligned}\nonumber \]
Because the last statement is true, we conclude that 7/6 is a solution of the equation x − 5/6 = 1/3.
Undoing Addition
You can still subtract the same amount from both sides of an equation without changing the solution.
Solve for x: \(x + \frac{2}{3} = - \frac{3}{5}\).
Solution
To “undo” adding 2/3, subtract 2/3 from both sides of the equation and simplify.
\[ \begin{aligned} x + \frac{2}{3} = - \frac{3}{5} ~ & \textcolor{red}{ \text{ Original equation.}} \\ x + \frac{2}{3} - \frac{2}{3} = - \frac{3}{5} - \frac{2}{3} ~ & \textcolor{red}{ \text{ Subtract } \frac{2}{3} \text{ from both sides.}} \\ x = - \frac{3 \cdot 3}{5 \cdot 3} - \frac{2 \cdot 5}{3 \cdot 5} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 15.}} \\ x = - \frac{9}{15} - \frac{10}{15} ~ & \textcolor{red}{ \text{ Simplify.}} \\ x = - \frac{19}{15} ~ & \textcolor{red}{ \text{ Subtract.}} \end{aligned}\nonumber \]
Readers are encouraged to check this solution in the original equation.
Solve for x: \(x + \frac{3}{4} = - \frac{1}{2}\)
- Answer
-
−5/4
Undoing Multiplication
We “undo” multiplication by dividing. For example, to solve the equation 2x = 6, we would divide both sides of the equation by 2. In similar fashion, we could divide both sides of the equation
\[ \frac{3}{5} x = \frac{4}{10}\nonumber \]
by 3/5. However, it is more efficient to take advantage of reciprocals. For convenience, we remind readers of the Multiplicative Inverse Property.
Let a/b be any fraction. The number b/a is called the multiplicative inverse or reciprocal of a/b. The product of reciprocals is 1.
\[ \frac{a}{b} \cdot \frac{b}{a} = 1.\nonumber \]
Let’s put our knowledge of reciprocals to work.
Solve for x: \(\frac{3}{5}x = \frac{4}{10}\).
Solution
To “undo” multiplying by 3/5, multiply both sides by the reciprocal 5/3 and simplify.
\[ \begin{aligned} \frac{3}{5} x = \frac{4}{10} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{5}{3} \left( \frac{3}{5} x \right) = \frac{5}{3} \left( \frac{4}{10} \right) & ~ \textcolor{red}{ \text{ Multiply both sides by 5/3.}} \\ \left( \frac{5}{3} \cdot \frac{3}{5} \right) x = \frac{20}{30} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, use the associative property to regroup.} \\ \text{ On the right, multiply.} \end{array}} \\ 1x = \frac{2}{3} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, } \frac{5}{3} \cdot \frac{3}{5} = 1. \\ \text{ On the right, reduce: } \frac{20}{30} = \frac{2}{3}. \end{array}} \\ x = \frac{2}{3} ~ & \textcolor{red}{ \text{ On the left, } 1x = x.} \end{aligned}\nonumber \]
Checking the Solution
Substitute 2/3 for x in the original equation and simplify.
\[ \begin{aligned} \frac{3}{5} x = \frac{4}{10} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{3}{5} \left( \frac{2}{3} \right) = \frac{4}{10} ~ & \textcolor{red}{ \text{ Substitute 2/3 for }x.} \\ \frac{6}{15} = \frac{4}{10} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ \frac{2}{5} = \frac{2}{5} ~ & \textcolor{red}{ \text{ Reduce both sides to lowest terms.}} \end{aligned}\nonumber \]
Because this last statement is true, we conclude that 2/3 is a solution of the equation (3/5)x = 4/10.
Solve for y: \( \frac{2}{3} y = \frac{4}{5}\)
- Answer
-
6/5
Solve for x: \(- \frac{8}{9} x = \frac{5}{18}\).
Solution
To “undo” multiplying by −8/9, multiply both sides by the reciprocal −9/8 and simplify.
\[ \begin{aligned} - \frac{8}{9} x = \frac{5}{18} ~ & \textcolor{red}{ \text{ Original equation.}} \\ - \frac{9}{8} \left( - \frac{8}{9} x \right) = - \frac{9}{8} \left( \frac{5}{18} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by } -9/8.} \\ \left[ - \frac{9}{8} \cdot \left( - \frac{8}{9} \right) \right] x = - \frac{3 \cdot 3}{2 \cdot 2 \cdot 2} \cdot \frac{5}{2 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, use the associative property to regroup.} \\ \text{ On the right, prime factor.} \end{array}} 1x = \frac{ \cancel{3} \cdot \cancel{3}}{2 \cdot 2 \cdot 2} \cdot \frac{5}{2 \cdot \cancel{3} \cdot \cancel{3}} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, } - \frac{9}{8} \cdot \left( - \frac{8}{9} \right) = 1. \\ \text{ On the right, cancel common factors.} \end{array}} \\ x = - \frac{5}{16} ~ & \textcolor{red}{ \text{ On the left, } 1x = x. \text{ Multiply on the right.}} \end{aligned}\nonumber \]
Readers are encouraged to check this solution in the original equation.
Solve for z: \(− \frac{2}{7} z = \frac{4}{21}\)
- Answer
-
−2/3
Clearing Fractions from the Equation
Although the technique demonstrated in the previous examples is a solid mathematical technique, working with fractions in an equation is not always the most efficient use of your time.
To clear all fractions from an equation, multiply both sides of the equation by the least common denominator of the fractions that appear in the equation.
Let’s put this idea to work.
In Example 1, we were asked to solve the following equation for x:
\[x - \frac{5}{6} = \frac{1}{3}.\nonumber \]
Take a moment to review the solution technique in Example 1. We will now solve this equation by first clearing all fractions from the equation.
Solution
Multiply both sides of the equation by the least common denominator for the fractions appearing in the equation.
\[ \begin{aligned} x - \frac{5}{6}= \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 6 \left( x - \frac{5}{6} \right) = 6 \left( \frac{1}{3} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 6.}} \\ 6x - 6 \left( \frac{5}{6} \right) = 6 \left( \frac{1}{3} \right) ~ & \textcolor{red}{ \text{ Distribute the 6.}} \\ 6x-5 = 2 ~ & \textcolor{red}{ \text{ On each side, multiply first.}} \\ ~ & \textcolor{red}{6 \left( \frac{5}{6} \right) = 5 \text{ and } 6 \left( \frac{1}{3} \right) = 2.} \end{aligned}\nonumber \]
Note that the equation is now entirely clear of fractions, making it a much simpler equation to solve.
\[ \begin{aligned} 6x - 5 + 5 = 2 + 5 ~ & \textcolor{red}{ \text{ Add 5 to both sides.}} \\ 6x = 7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{6x}{6} = \frac{7}{6} ~ & \textcolor{red}{ \text{ Divide both sides by 6.}} \\ x = \frac{7}{6} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Note that this is the same solution found in Example 1.
Solve for t: \(t - \frac{2}{7} = - \frac{1}{4}\)
- Answer
-
1/28
In Example 4, we were asked to solve the following equation for x.
\[- \frac{8}{9}x = \frac{5}{18}\nonumber \]
Take a moment to review the solution in Example 4. We will now solve this equation by first clearing all fractions from the equation.
Solution
Multiply both sides of the equation by the least common denominator for the fractions that appear in the equation.
\[ \begin{aligned} - \frac{8}{9} x = \frac{5}{18} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 18 \left( - \frac{8}{9} x \right) = 18 \left( \frac{5}{18} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 18.}} \\ -16x=5 ~ & \textcolor{red}{ \text{ On each side, cancel and multiply.}} \\ ~ & \textcolor{red}{ 18 \left( - \frac{8}{9} \right) = -16 \text{ and } 18 \left( \frac{5}{18} \right) = 5.} \end{aligned}\nonumber \]
Note that the equation is now entirely free of fractions. Continuing,
\[ \begin{aligned} \frac{-16x}{-16} = \frac{5}{-16} ~ & \textcolor{red}{ \text{ Divide both sides by } -16.} \\ x = - \frac{5}{16} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Note that this is the same as the solution found in Example 4.
Solve for u:
\[ - \frac{7}{9} u = \frac{14}{27}\nonumber \]
- Answer
-
−2/3
Solve for x: \(\frac{2}{3}x + \frac{3}{4} = \frac{1}{2}\).
Solution
Multiply both sides of the equation by the least common denominator for the fractions appearing in the equation.
\[ \begin{aligned} \frac{2}{3} x + \frac{3}{4} = \frac{1}{2} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 12 \left( \frac{2}{3} x + \frac{3}{4} = \right) = 12 \left( \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 12.}} \\ 12 \left( \frac{2}{3}x \right) + 12 \left( \frac{3}{4} \right) = 12 \left( \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ On the left, distribute 12.}} \\ 8x + 9 = 6 ~ & \textcolor{red}{ \text{ Multiply: } 12 \left( \frac{2}{3} x \right) = 8x, ~ 12 \left( \frac{3}{4} \right) = 9,} \\ ~ & \textcolor{red}{ \text{ and } 12 \left( \frac{1}{2} \right) = 6.} \end{aligned}\nonumber \]
Note that the equation is now entirely free of fractions. We need to isolate the terms containing x on one side of the equation.
\[ \begin{aligned} 8x + 9 - 9 = 6 - 9 ~ & \textcolor{red}{ \text{ Subtract 9 from both sides.}} \\ 8x = - 3 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{8x}{8} = \frac{-3}{8} ~ & \textcolor{red}{ \text{ Divide both sides by 8.}} \\ x = - \frac{3}{8} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Readers are encouraged to check this solution in the original equation.
Solve for r: \(\frac{3}{4} r + \frac{2}{3} = \frac{1}{2}\)
- Answer
-
−2/9
Solve for x: \( \frac{2}{3} - \frac{3x}{4} = \frac{x}{2} - \frac{1}{8}.\)
Solution
Multiply both sides of the equation by the least common denominator for the fractions in the equation.
\[ \begin{aligned} \frac{2}{3} - \frac{3x}{4} = \frac{x}{2} - \frac{1}{8} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 24 \left( \frac{2}{3} - \frac{3x}{4} \right) = 24 \left( \frac{x}{2} - \frac{1}{8} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 24.}} \\ 24 \left( \frac{2}{3} \right) - 24 \left( \frac{3x}{4} \right) = 24 \left( \frac{x}{2} \right) - 24 \left( \frac{1}{8} \right) ~ & \textcolor{red}{ \text{ On both sides, distribute 24.}} \\ 16 - 18x = 12x - 3 ~ & \textcolor{red}{ \text{ Left: } 24 \left( \frac{2}{3} \right) = 16, ~ 24 \left( \frac{3x}{4} \right) = 18x.} \\ ~ & \textcolor{red}{ \text{ Right: } 24 \left( \frac{x}{2} \right) = 12x, ~ 24 \left( \frac{1}{8} \right) = 3.} \end{aligned}\nonumber \]
Note that the equation is now entirely free of fractions. We need to isolate the terms containing x on one side of the equation.
\[ \begin{aligned} 16 - 18x - 12x = 12x - 3 - 12x ~ & \textcolor{red}{ \text{ Subtract } 12x \text{ from both sides.}} \\ 16 - 30x = -3 ~ & \textcolor{red}{ \begin{aligned} \text{ Left: } -18x - 12x = -30x. \\ \text{ Right: } 12x - 12x = 0. \end{aligned}} \\ 16 - 30x - 16 = -3 - 16 ~ & \textcolor{red}{ \text{ Subtract 16 from both sides.}} \\ -30x = -19 ~ & \textcolor{red}{ \begin{aligned} \text{ Left: } 16-16=0. \\ \text{ Right: } -3 - 16 = -19. \end{aligned}} \\ \frac{-30x}{-30} = \frac{-19}{-30} ~ & \textcolor{red}{ \text{ Divide both sides by } -30.} \\ x = \frac{19}{30} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Readers are encouraged to check this solution in the original equation.
Solve for s: \( \frac{3}{2} - \frac{2s}{5} = \frac{s}{3} - \frac{1}{5}\).
- Answer
-
Add texts here. Do not delete this text first.
Applications
Let’s look at some applications that involve equations containing fractions. For convenience, we repeat the Requirements for Word Problem Solutions.
- Set up a Variable Dictionary. You must let your readers know what each variable in your problem represents. This can be accomplished in a number of ways:
- Statements such as “Let P represent the perimeter of the rectangle.”
- Labeling unknown values with variables in a table.
- Labeling unknown quantities in a sketch or diagram.
- Set up an Equation. Every solution to a word problem must include a carefully crafted equation that accurately describes the constraints in the problem statement.
- Solve the Equation. You must always solve the equation set up in the previous step.
- Answer the Question. This step is easily overlooked. For example, the problem might ask for Jane’s age, but your equation’s solution gives the age of Jane’s sister Liz. Make sure you answer the original question asked in the problem. Your solution should be written in a sentence with appropriate units. 5. Look Back. It is important to note that this step does not imply that you should simply check your solution in your equation. After all, it’s possible that your equation incorrectly models the problem’s situation, so you could have a valid solution to an incorrect equation. The important question is: “Does your answer make sense based on the words in the original problem statement.”
In the third quarter of a basketball game, announcers informed the crowd that attendance for the game was 12,250. If this is two-thirds of the capacity, find the full seating capacity for the basketball arena.
Solution
We follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. Let F represent the full seating capacity. Note: It is much better to use a variable that “sounds like” the quantity that it represents. In this case, letting F represent the full seating capacity is much more descriptive than using x to represent the full seating capacity.
2. Set up an Equation. Two-thirds of the full seating capacity is 12,250.
\[ \begin{aligned} \colorbox{cyan}{Two-thirds} & \text{ of } & \colorbox{cyan}{Full Seating Capacity} & \text{ is } & 12,250 \\ \frac{2}{3} & \cdot & F & = & 12,250 \end{aligned}\nonumber \]
Hence, the equation is
\[ \frac{2}{3} F = 12250.\nonumber \]
3. Solve the Equation. Multiply both sides by 3 to clear fractions, then solve.
\[ \begin{aligned} \frac{2}{3} F = 12250 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3 \left( \frac{2}{3} F \right) = 3(12250) ~ & \textcolor{red}{ \text{ Multiply both sides by 3.}} \\ 2F = 36750 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{2F}{2} = \frac{36750}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ F = 18375 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
4. Answer the Question. The full seating capacity is 18,375.
5. Look Back. The words of the problem state that 2/3 of the seating capacity is 12,250. Let’s take two-thirds of our answer and see what we get.
\[ \begin{aligned} \frac{2}{3} \cdot 18375 & = \frac{2}{3} \cdot \frac{18375}{1} \\ & = \frac{2}{3} \cdot \frac{3 \cdot 6125}{1} \\ & = \frac{2}{ \cancel{3}} \cdot \frac{ \cancel{3} \cdot 6125}{1} \\ & = 12250 \end{aligned}\nonumber \]
This is the correct attendance, so our solution is correct.
Attendance for the Celtics game was 9,510. If this is 3/4 of capacity, what is the capacity of the Celtics’ arena?
- Answer
-
12,680
The area of a triangle is 20 square inches. If the length of the base is \(2 \frac{1}{2}\) inches, find the height (altitude) of the triangle.
Solution
We follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. Our variable dictionary will take the form of a well labeled diagram.
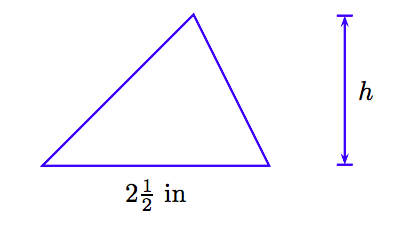
2. Set up an Equation. The area A of a triangle with base b and height h is
\[A = \frac{1}{2} bh.\nonumber \]
Substitute A = 20 and b = \(2 \frac{1}{2}\).
\[20 = \frac{1}{2} \left( 2 \frac{1}{2} \right) h.\nonumber \]
3. Solve the Equation. Change the mixed fraction to an improper fraction, then simplify.
\[ \begin{aligned} 20 = \frac{1}{2} \left( 2 \frac{1}{2} \right) h ~ & \textcolor{red}{ \text{ Original equation.}} \\ 20 = \frac{1}{2} \left( \frac{5}{2} \right) h ~ & \textcolor{red}{ \text{ Mixed to improper: } 2 \frac{1}{2} = \frac{5}{2}.} \\ 20 = \left( \frac{1}{2} \cdot \frac{5}{2} \right) h ~ & \textcolor{red}{ \text{ Associative property.}} \\ 20 = \frac{5}{4} h ~ & \textcolor{red}{ \text{ Multiply: } \frac{1}{2} \cdot \frac{5}{2} = \frac{5}{4}.} \end{aligned}\nonumber \]
Now, multiply both sides by 4/5 and solve.
\[ \begin{aligned} \frac{4}{5} (20) = \frac{4}{5} \left( \frac{5}{4} h \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 4/5.}} \\ 16 = h ~ & \textcolor{red}{ \text{ Simplify: } \frac{4}{5} (20) = 16} \\ ~ & \textcolor{red}{ \text{ and } \frac{4}{5} \cdot \frac{5}{4} = 1.} \end{aligned}\nonumber \]
4. Answer the Question. The height of the triangle is 16 inches.
5. Look Back. If the height is 16 inches and the base is \(2 \frac{1}{2}\) inches, then the area is
\[ \begin{aligned} A & = \frac{1}{2} \left( 2 \frac{1}{2} \right) (16) \\ & = \frac{1}{2} \cdot \frac{5}{2} \cdot \frac{16}{1} \\ & = \frac{5 \cdot 16}{2 \cdot 2} \\ & = \frac{(5) \cdot (2 \cdot 2 \cdot 2 \cdot 2)}{(2) \cdot (2)} \\ & = \frac{5 \cdot \cancel{2} \cdot \cancel{2} \cdot 2 \cot 2}{ \cancel{2} \cdot \cancel{2}} & = 20 \end{aligned}\nonumber \]
This is the correct area (20 square inches), so our solution is correct.
The area of a triangle is 161 square feet. If the base of the triangle measures \(40 \frac{1}{4}\) feet, find the height of the triangle.
- Answer
-
8 feet
Exercises
1. Is 1/4 a solution of the equation \(x + \frac{5}{8} = \frac{5}{8}\)?
2. Is 1/4 a solution of the equation \(x + \frac{1}{3} = \frac{5}{12}\)?
3. Is −8/15 a solution of the equation \(\frac{1}{4} x = − \frac{1}{15}\)?
4. Is −18/7 a solution of the equation \(− \frac{3}{8} x = \frac{25}{28}\)?
5. Is 1/2 a solution of the equation \(x + \frac{4}{9} = \frac{17}{18}\)?
6. Is 1/3 a solution of the equation \(x + \frac{3}{4} = \frac{13}{12}\)?
7. Is 3/8 a solution of the equation \(x − \frac{5}{9} = − \frac{13}{72}\)?
8. Is 1/2 a solution of the equation \(x − \frac{3}{5} = − \frac{1}{10}\)?
9. Is 2/7 a solution of the equation \(x − \frac{4}{9} = − \frac{8}{63}\)?
10. Is 1/9 a solution of the equation \(x − \frac{4}{7} = − \frac{31}{63}\)?
11. Is 8/5 a solution of the equation \( \frac{11}{14}x = \frac{44}{35}\)?
12. Is 16/9 a solution of the equation \(\frac{13}{18} x = \frac{104}{81}\)?
In Exercises 13-24, solve the equation and simplify your answer.
13. \(2x − 3=6x + 7\)
14. \(9x − 8 = −9x − 3\)
15. \(−7x +4=3x\)
16. \(6x +9= −6x\)
17. \(−2x = 9x − 4\)
18. \(−6x = −9x + 8\)
19. \(−8x = 7x − 7\)
20. \(−6x = 5x + 4\)
21. \(−7x +8=2x\)
22. \(−x − 7=3x\)
23. \(−9x +4=4x − 6\)
24. \(−2x +4= x − 7\)
In Exercises 25-48, solve the equation and simplify your answer.
25. \(x + \frac{3}{2 = \frac{1}{2}\)
26. \(x − \frac{3}{4} = \frac{1}{4}\)
27. \(− \frac{9}{5} x = \frac{1}{2}\)
28. \(\frac{7}{3} x = − \frac{7}{2}\)
29. \(\frac{3}{8} x = \frac{8}{7}\)
30. \(− \frac{1}{9} x = − \frac{3}{5}\)
31. \(\frac{2}{5} x = − \frac{1}{6}\)
32. \(\frac{1}{6} x = \frac{2}{9}\)
33. \(− \frac{3}{2} x = \frac{8}{7}\)
34. \(− \frac{3}{2} x = − \frac{7}{5}\)
35. \(x + \frac{3}{4} = \frac{5}{9}\)
36. \(x − \frac{1}{9} = − \frac{3}{2}\)
37. \(x − \frac{4}{7} = \frac{7}{8}\)
38. \(x + \frac{4}{9} = − \frac{3}{4}\)
39. \(x + \frac{8}{9} = \frac{2}{3}\)
40. \(x − \frac{5}{6} = \frac{1}{4}\)
41. \(x + \frac{5}{2} = − \frac{9}{8}\)
42. \(x + \frac{1}{2} = \frac{5}{3}\)
43. \(− \frac{8}{5} x = \frac{7}{9}\)
44. \(− \frac{3}{2} x = − \frac{5}{9}\)
45. \(x − \frac{1}{4} = − \frac{1}{8}\)
46. \(x − \frac{9}{2} = − \frac{7}{2}\)
47. \(− \frac{1}{4} x = \frac{1}{2}\)
48. \(− \frac{8}{9} x = − \frac{8}{3}\)
In Exercises 49-72, solve the equation and simplify your answer.
49. \(− \frac{7}{3} x − \frac{2}{3} = \frac{3}{4} x + \frac{2}{3}\)
50. \(\frac{1}{2} x − \frac{1}{2} = \frac{3}{2} x + \frac{3}{4}\)
51. \(− \frac{7}{2} x − \frac{5}{4} = \frac{4}{5}\)
52. \(− \frac{7}{6} x + \frac{5}{6} = − \frac{8}{9}\)
53. \(− \frac{9}{7} x + \frac{9}{2} = − \frac{5}{2}\)
54. \(\frac{5}{9} x − \frac{7}{2} = \frac{1}{4}\)
55. \(\frac{1}{4} x − \frac{4}{3} = − \frac{2}{3}\)
56. \(\frac{8}{7} x + \frac{3}{7} = \frac{5}{3}\)
57. \(\frac{5}{3} x + \frac{3}{2} = − \frac{1}{4}\)
58. \(\frac{1}{2} x − \frac{8}{3} = − \frac{2}{5}\)
59. \(− \frac{1}{3} x + \frac{4}{5} = − \frac{9}{5} x − \frac{5}{6}\)
60. \(− \frac{2}{9} x − \frac{3}{5} = \frac{4}{5} x − \frac{3}{2}\)
61. \(− \frac{4}{9} x − \frac{8}{9} = \frac{1}{2} x − \frac{1}{2}\)
62. \(− \frac{5}{4} x − \frac{5}{3} = \frac{8}{7} x + \frac{7}{3}\)
63. \(\frac{1}{2} x − \frac{1}{8} = − \frac{1}{8} x + \frac{5}{7}\)
64. \(− \frac{3}{2} x + \frac{8}{3} = \frac{7}{9} x − \frac{1}{2}\)
65. \(− \frac{3}{7} x − \frac{1}{3} = − \frac{1}{9}\)
66. \(\frac{2}{3} x + \frac{2}{9} = − \frac{9}{5}\)
67. \(− \frac{3}{4} x + \frac{2}{7} = \frac{8}{7} x − \frac{1}{3}\)
68. \(\frac{1}{2} x + \frac{1}{3} = − \frac{5}{2} x − \frac{1}{4}\)
69. \(− \frac{3}{4} x − \frac{2}{3} = − \frac{2}{3} x − \frac{1}{2}\)
70. \(\frac{1}{3} x − \frac{5}{7} = \frac{3}{2} x + \frac{4}{3}\)
71. \(− \frac{5}{2} x + \frac{9}{5} = \frac{5}{8}\)
72. \(\frac{9}{4} x + \frac{4}{3} = − \frac{1}{6}\)
73. At a local soccer game, announcers informed the crowd that attendance for the game was 4,302. If this is 2/9 of the capacity, find the full seating capacity for the soccer stadium.
74. At a local basketball game, announcers informed the crowd that attendance for the game was 5,394. If this is 2/7 of the capacity, find the full seating capacity for the basketball stadium.
75. The area of a triangle is 51 square inches. If the length of the base is \(8 \frac{1}{2}\) inches, find the height (altitude) of the triangle.
76. The area of a triangle is 20 square inches. If the length of the base is \(2 \frac{1}{2}\) inches, find the height (altitude) of the triangle.
77. The area of a triangle is 18 square inches. If the length of the base is \(4 \frac{1}{2}\) inches, find the height (altitude) of the triangle.
78. The area of a triangle is 44 square inches. If the length of the base is \(5 \frac{1}{2}\) inches, find the height (altitude) of the triangle.
79. At a local hockey game, announcers informed the crowd that attendance for the game was 4,536. If this is 2/11 of the capacity, find the full seating capacity for the hockey stadium.
80. At a local soccer game, announcers informed the crowd that attendance for the game was 6,970. If this is 2/7 of the capacity, find the full seating capacity for the soccer stadium.
81. Pirates. About one-third of the world’s pirate attacks in 2008 occurred off the Somali coast. If there were 111 pirate attacks off the Somali coast, estimate the number of pirate attacks worldwide in 2008.
82. Nuclear arsenal. The U.S. and Russia agreed to cut nuclear arsenals of long-range nuclear weapons by about a third, down to 1, 550. How many long-range nuclear weapons are there now? Associated Press-Times-Standard 04/04/10 Nuclear heartland anxious about missile cuts.
83. Seed vault. The Svalbard Global Seed Vault has amassed half a million seed samples, and now houses at least one-third of the world’s crop seeds. Estimate the total number of world’s crop seeds. Associated Press-Times-Standard 03/15/10 Norway doomsday seed vault hits half-million mark.
84. Freight train. The three and one-half mile long Union Pacific train is about 2 1 2 times the length of a typical freight train. How long is a typical freight train? Associated Press-Times-Standard 01/13/10 Unusally long train raises safety concerns.
Answers
1. No
3. No
5. Yes
7. Yes
9. No
11. Yes
13. \(− \frac{5}{2}\)
15. \(\frac{2}{5}\)
17. \(\frac{4}{11}\)
19. \(\frac{7}{15}\)
21. \(\frac{8}{9}\)
23. \(\frac{10}{13}\)
25. \(−1\)
27. \(− \frac{5}{18}\)
29. \(\frac{64}{21}\)
31. \(− \frac{5}{12}\)
33. \(− \frac{16}{21}\)
35. \(− \frac{7}{36}\)
37. \(\frac{81}{56}\)
39. \(− \frac{2}{9}\)
41. \(− \frac{29}{8}\)
43. \(− \frac{35}{72}\)
45. \(\frac{1}{8}\)
47. \(−2\)
49. \(− \frac{16}{37}\)
51. \(− \frac{41}{70}\)
53. \(\frac{49}{9}\)
55. \(\frac{8}{3}\)
57. \(− \frac{21}{20}\)
59. \(− \frac{49}{44}\)
61. \(− \frac{7}{17}\)
63. \(\frac{47}{35}\)
65. \(− \frac{14}{27}\)
67. \(\frac{52}{159}\)
69. \(− 2\)
71. \(\frac{47}{100}\)
73. 19,359
75. 12
77. 8
79. 24,948
81. There were about 333 pirate attacks worldwide.
83. 1,500,000


