7.2: Addition and Subtraction Identities

Section 7.2 Addition and Subtraction Identities

In this section, we begin expanding our repertoire of trigonometric identities.

IDENTITIES

The sum and difference identities

\(\cos (\alpha -\beta )=\cos (\alpha )\cos (\beta )+\sin (\alpha )\sin (\beta )\)

\(\cos (\alpha +\beta )=\cos (\alpha )\cos (\beta )-\sin (\alpha )\sin (\beta )\)

\(\sin (\alpha +\beta )=\sin (\alpha )\cos (\beta )+\cos (\alpha )\sin (\beta )\)

\(\sin (\alpha -\beta )=\sin (\alpha )\cos (\beta )-\cos (\alpha )\sin (\beta )\)

We will prove the difference of angles identity for cosine. The rest of the identities can be derived from this one.

Proof of the difference of angles identity for cosine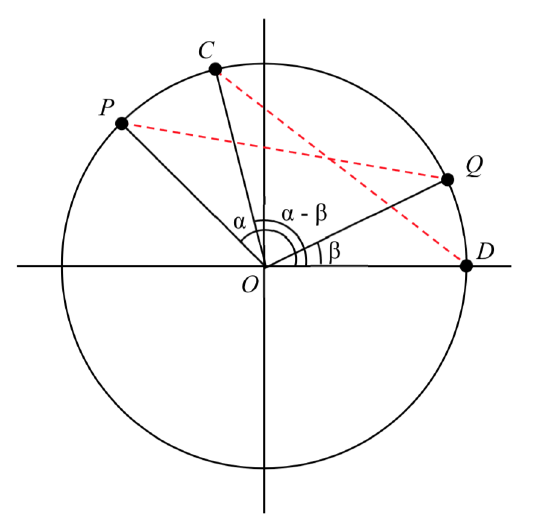

Consider two points on a unit circle:

\(P\) at an angle of \(\alpha\) from the positive \(x\) axis with coordinates \(\left(\cos (\alpha ),\sin (\alpha )\right)\), and \(Q\) at an angle of \(\beta\) with coordinates \(\left(\cos (\beta ),\sin (\beta)\right)\).

Notice the measure of angle \(POQ\) is \(\alpha\) – \(\beta\). Label two more points:

\(C\) at an angle of \(\alpha\) – \(\beta\), with coordinates \(\left(\cos (\alpha -\beta ),\sin (\alpha -\beta )\right)\),

\(D\) at the point (1, 0).

Notice that the distance from \(C\) to \(D\) is the same as the distance from \(P\) to \(Q\) because triangle \(COD\) is a rotation of triangle \(POQ\).

Using the distance formula to find the distance from \(P\) to \(Q\) yields

\(\sqrt{\left(\cos (\alpha )-\cos (\beta )\right)^{2} +\left(\sin (\alpha )-\sin (\beta )\right)^{2} }\)

Expanding this

\(\sqrt{\cos ^{2} (\alpha )-2\cos (\alpha )\cos (\beta )+\cos ^{2} (\beta )+\sin ^{2} (\alpha )-2\sin (\alpha )\sin (\beta )+\sin ^{2} (\beta )}\)

Applying the Pythagorean Identity and simplifying

\(\sqrt{2-2\cos (\alpha )\cos (\beta )-2\sin (\alpha )\sin (\beta )}\)

Similarly, using the distance formula to find the distance from \(C\) to \(D\)

\(\sqrt{\left(\cos (\alpha -\beta )-1\right)^{2} +\left(\sin (\alpha -\beta )-0\right)^{2} }\)

Expanding this

\(\sqrt{\cos ^{2} (\alpha -\beta )-2\cos (\alpha -\beta )+1+\sin ^{2} (\alpha -\beta )}\)

Applying the Pythagorean Identity and simplifying

\(\sqrt{-2\cos (\alpha -\beta )+2}\)

Since the two distances are the same we set these two formulas equal to each other and simplify

\(\sqrt{2-2\cos (\alpha )\cos (\beta )-2\sin (\alpha )\sin (\beta )} =\sqrt{-2\cos (\alpha -\beta )+2}\)
\(2-2\cos (\alpha )\cos (\beta )-2\sin (\alpha )\sin (\beta )=-2\cos (\alpha -\beta )+2\)
\(\cos (\alpha )\cos (\beta )+\sin (\alpha )\sin (\beta )=\cos (\alpha -\beta )\)

This establishes the identity.

Exercise

By writing \(\cos (\alpha +\beta )\) as \(\cos \left(\alpha -\left(-\beta \right)\right)\), show the sum of angles identity for cosine follows from the difference of angles identity proven above.

Answer

\(\begin{array}{l} {\cos (\alpha +\beta )=\cos (\alpha -(-\beta ))} \\ {\cos (\alpha )\cos (-\beta )+\sin (\alpha )\sin (-\beta )} \\ {\cos (\alpha )\cos (\beta )+\sin (\alpha )(-\sin (\beta ))} \\ {\cos (\alpha )\cos (\beta )-\sin (\alpha )\sin (\beta )} \end{array}\)

The sum and difference of angles identities are often used to rewrite expressions in other forms, or to rewrite an angle in terms of simpler angles.

EXAMPLE 1

Find the exact value of \(\cos (75{}^\circ )\).

Solution

Since \(75{}^\circ =30{}^\circ +45{}^\circ\), we can evaluate \(\cos (75{}^\circ )\) as

\(\cos (75{}^\circ )=\cos (30{}^\circ +45{}^\circ )\) Apply the cosine sum of angles identity
\(=\cos (30{}^\circ )\cos (45{}^\circ )-\sin (30{}^\circ )\sin (45{}^\circ )\) Evaluate
\(=\frac{\sqrt{3} }{2} \cdot \frac{\sqrt{2} }{2} -\frac{1}{2} \cdot \frac{\sqrt{2} }{2}\) Simply
\(=\frac{\sqrt{6} -\sqrt{2} }{4}\)

Exercise

Find the exact value of \(\sin \left(\frac{\pi }{12} \right)\).

Answer

\(\sin \left(\frac{\pi }{12} \right)=\sin \left(\frac{\pi }{3} -\frac{\pi }{4} \right)=\sin \left(\frac{\pi }{3} \right)\cos \left(\frac{\pi }{4} \right)-\cos \left(\frac{\pi }{3} \right)\sin \left(\frac{\pi }{4} \right)\)
\(=\frac{\sqrt{3} }{2} \frac{\sqrt{2} }{2} -\frac{1}{2} \frac{\sqrt{2} }{2}\) \(\frac{\sqrt{6} -\sqrt{2} }{4}\)

EXAMPLE 2

Rewrite \(\sin \left(x-\frac{\pi }{4} \right)\) in terms of sin(\(x\)) and cos(\(x\)).

Solution

\(\sin \left(x-\frac{\pi }{4} \right)\) Use the difference of angles identity for sine
= \(\sin \left(x\right)\cos \left(\frac{\pi }{4} \right)-\cos \left(x\right)\sin \left(\frac{\pi }{4} \right)\) Evaluate the cosine and sine and rearrange
\(=\frac{\sqrt{2} }{2} \sin \left(x\right)-\frac{\sqrt{2} }{2} \cos \left(x\right)\)

Additionally, these identities can be used to simplify expressions or prove new identities

EXAMPLE 3

Prove \(\frac{\sin (a+b)}{\sin (a-b)} =\frac{\tan (a)+\tan (b)}{\tan (a)-\tan (b)}\).

Solution

As with any identity, we need to first decide which side to begin with. Since the left side involves sum and difference of angles, we might start there

\(\frac{\sin (a+b)}{\sin (a-b)}\) Apply the sum and difference of angle identities
\(=\frac{\sin (a)\cos (b)+\cos (a)\sin (b)}{\sin (a)\cos (b)-\cos (a)\sin (b)}\)

Since it is not immediately obvious how to proceed, we might start on the other side, and see if the path is more apparent.

\(\frac{\tan (a)+\tan (b)}{\tan (a)-\tan (b)}\) Rewriting the tangents using the tangent identity
\(=\frac{\frac{\sin (a)}{\cos (a)} +\frac{\sin (b)}{\cos (b)} }{\frac{\sin (a)}{\cos (a)} -\frac{\sin (b)}{\cos (b)} }\) Multiplying the top and bottom by cos(\(a\))cos(\(b\))
\(=\frac{\left(\frac{\sin (a)}{\cos (a)} +\frac{\sin (b)}{\cos (b)} \right)\cos (a)\cos (b)}{\left(\frac{\sin (a)}{\cos (a)} -\frac{\sin (b)}{\cos (b)} \right)\cos (a)\cos (b)}\) Distributing and simplifying
\(=\frac{\sin (a)\cos (b)+\sin (b)\cos (a)}{\sin (a)\cos (b)-\sin (b)\cos (a)}\) From above, we recognize this
\(=\frac{\sin (a+b)}{\sin (a-b)}\) Establishing the identity

These identities can also be used to solve equations.

EXAMPLE 4

Solve \(\sin (x)\sin (2x)+\cos (x)\cos (2x)=\frac{\sqrt{3} }{2}\).

Solution

By recognizing the left side of the equation as the result of the difference of angles identity for cosine, we can simplify the equation

\(\sin (x)\sin (2x)+\cos (x)\cos (2x)=\frac{\sqrt{3} }{2}\) Apply the difference of angles identity
\(\cos (x-2x)=\frac{\sqrt{3} }{2}\)
\(\cos (-x)=\frac{\sqrt{3} }{2}\) Use the negative angle identity
\(\cos (x)=\frac{\sqrt{3} }{2}\)

Since this is a special cosine value we recognize from the unit circle, we can quickly write the answers:

\(\begin{array}{l} {x=\frac{\pi }{6} +2\pi k} \\ {x=\frac{11\pi }{6} +2\pi k} \end{array}\), where \(k\) is an integer

Combining Waves of Equal Period

A sinusoidal function of the form \(f(x)=A\sin (Bx+C)\) can be rewritten using the sum of angles identity.

EXAMPLE 5

Rewrite \(f(x)=4\sin \left(3x+\frac{\pi }{3} \right)\) as a sum of sine and cosine.

Solution

\(4\sin \left(3x+\frac{\pi }{3} \right)\) Using the sum of angles identity
\(=4\left(\sin \left(3x\right)\cos \left(\frac{\pi }{3} \right)+\cos \left(3x\right)\sin \left(\frac{\pi }{3} \right)\right)\) Evaluate the sine and cosine
\(=4\left(\sin \left(3x\right)\cdot \frac{1}{2} +\cos \left(3x\right)\cdot \frac{\sqrt{3} }{2} \right)\) Distribute and simplify
\(=2\sin \left(3x\right)+2\sqrt{3} \cos \left(3x\right)\)

Notice that the result is a stretch of the sine added to a different stretch of the cosine, but both have the same horizontal compression, which results in the same period.

We might ask now whether this process can be reversed – can a combination of a sine and cosine of the same period be written as a single sinusoidal function? To explore this, we will look in general at the procedure used in the example above.

\(f(x)=A\sin (Bx+C)\) Use the sum of angles identity
\(=A\left(\sin (Bx)\cos (C)+\cos (Bx)\sin (C)\right)\) Distribute the \(A\)
\(=A\sin (Bx)\cos (C)+A\cos (Bx)\sin (C)\) Rearrange the terms a bit
\(=A\cos (C)\sin (Bx)+A\sin (C)\cos (Bx)\)

Based on this result, if we have an expression of the form \(m\sin (Bx)+n\cos (Bx)\), we could rewrite it as a single sinusoidal function if we can find values A and C so that

\(m\sin (Bx)+n\cos (Bx)\) \(=A\cos (C)\sin (Bx)+A\sin (C)\cos (Bx)\), which will require that:

\(\begin{array}{l} {m=A\cos (C)} \\ {n=A\sin (C)} \end{array}\) which can be rewritten as \(\begin{array}{l} {\frac{m}{A} =\cos (C)} \\ {\frac{n}{A} =\sin (C)} \end{array}\)

To find \(A\),

\(m^{2} +n^{2} =\left(A\cos (C)\right)^{2} +\left(A\sin (C)\right)^{2}\)
\(=A^{2} \cos ^{2} (C)+A^{2} \sin ^{2} (C)\)
\(=A^{2} \left(\cos ^{2} (C)+\sin ^{2} (C)\right)\) Apply the Pythagorean Identity and simplify
\(=A^{2}\)

REWRITING A SUM OF SINE AND COSINE AS A SINGLE SINE

To rewrite \(m\sin (Bx)+n\cos (Bx)\) as \(A\sin (Bx+C)\)

\(A^{2} =m^{2} +n^{2}\), \(\cos (C)=\frac{m}{A}\), and \(\sin (C)=\frac{n}{A}\)

You can use either of the last two equations to solve for possible values of C. Since there will usually be two possible solutions, we will need to look at both to determine which quadrant C is in and determine which solution for C satisfies both equations.

EXAMPLE 6

Rewrite \(4\sqrt{3} \sin (2x)-4\cos (2x)\) as a single sinusoidal function.

Solution

Using the formulas above, \(A^{2} =\left(4\sqrt{3} \right)^{2} +\left(-4\right)^{2} =16\cdot 3+16=64\), so \(A = 8\).

Solving for \(C\),

\(\cos (C)=\frac{4\sqrt{3} }{8} =\frac{\sqrt{3} }{2}\), so \(C=\frac{\pi }{6}\) or \(C=\frac{11\pi }{6}\).

However, notice \(\sin (C)=\frac{-4}{8} =-\frac{1}{2}\). Sine is negative in the third and fourth quadrant, so the angle that works for both is \(C=\frac{11\pi }{6}\).

Combining these results gives us the expression

\(8\sin \left(2x+\frac{11\pi }{6} \right)\)

Exercise

Rewrite \(-3\sqrt{2} \sin (5x)+3\sqrt{2} \cos (5x)\) as a single sinusoidal function.

Answer

\(A^{2} =\left(-3\sqrt{2} \right)^{2} +\left(3\sqrt{2} \right)^{2} =36\). \(A = 6\)
\(\cos (C)=\frac{-3\sqrt{2} }{6} =\frac{-\sqrt{2} }{2}\), \(\sin (C)=\frac{3\sqrt{2} }{6} =\frac{\sqrt{2} }{2}\). \(C=\frac{3\pi }{4}\)
\(6\sin \left(5x+\frac{3\pi }{4} \right)\)

Rewriting a combination of sine and cosine of equal periods as a single sinusoidal function provides an approach for solving some equations.

EXAMPLE 7

Solve \(3\sin (2x)+4\cos (2x)=1\) to find two positive solutions.

Solution

Since the sine and cosine have the same period, we can rewrite them as a single sinusoidal function.

\(A^{2} =\left(3\right)^{2} +\left(4\right)^{2} =25\), so \(A = 5\)

\(\cos (C)=\frac{3}{5}\), so \(C=\cos ^{-1} \left(\frac{3}{5} \right)\approx 0.927\) or \(C=2\pi -0.927=5.356\)

Since \(\sin (C)=\frac{4}{5}\), a positive value, we need the angle in the first quadrant, \(C = 0.927\).

Using this, our equation becomes

\(5\sin \left(2x+0.927\right)=1\) Divide by 5
\(\sin \left(2x+0.927\right)=\frac{1}{5}\) Make the substitution \(u = 2x + 0.927\)
\(\sin \left(u\right)=\frac{1}{5}\) The inverse gives a first solution
\(u=\sin ^{-1} \left(\frac{1}{5} \right)\approx 0.201\) By symmetry, the second solution is
\(u=\pi -0.201=2.940\) A third solution would be
\(u=2\pi +0.201=6.485\)

Undoing the substitution, we can find two positive solutions for \(x\).

\(2x+0.927=0.201\) or \(2x+0.927=2.940\) or \(2x+0.927=6.485\)
\(2x=-0.726\) \(2x=2.013\) \(2x=5.558\)
\(x=-0.363\) \(x=1.007\) \(x=2.779\)

Since the first of these is negative, we eliminate it and keep the two positive solutions, \(x=1.007\) and \(x=2.779\).

The Product-to-Sum and Sum-to-Product Identities

IDENTITIES

The Product-to-Sum Identities

\(\begin{array}{l} {\sin (\alpha )\cos (\beta )=\frac{1}{2} \left(\sin (\alpha +\beta )+\sin (\alpha -\beta )\right)} \\ {\sin (\alpha )\sin (\beta )=\frac{1}{2} \left(\cos (\alpha -\beta )-\cos (\alpha +\beta )\right)} \\ {\cos (\alpha )\cos (\beta )=\frac{1}{2} \left(\cos (\alpha +\beta )+\cos (\alpha -\beta )\right)} \end{array}\)

We will prove the first of these, using the sum and difference of angles identities from the beginning of the section. The proofs of the other two identities are similar and are left as an exercise.

Proof of the product-to-sum identity for sin(\(\alpha\))cos(\(\beta\))

Recall the sum and difference of angles identities from earlier

\(\sin (\alpha +\beta )=\sin (\alpha )\cos (\beta )+\cos (\alpha )\sin (\beta )\)
\(\sin (\alpha -\beta )=\sin (\alpha )\cos (\beta )-\cos (\alpha )\sin (\beta )\)

Adding these two equations, we obtain

\(\sin (\alpha +\beta )+\sin (\alpha -\beta )=2\sin (\alpha )\cos (\beta )\)

Dividing by 2, we establish the identity

\(\sin (\alpha )\cos (\beta )=\frac{1}{2} \left(\sin (\alpha +\beta )+\sin (\alpha -\beta )\right)\)

EXAMPLE 8

Write \(\sin (2t)\sin (4t)\) as a sum or difference.

Solution

Using the product-to-sum identity for a product of sines

\(\sin (2t)\sin (4t)=\frac{1}{2} \left(\cos (2t-4t)-\cos (2t+4t)\right)\)
\(=\frac{1}{2} \left(\cos (-2t)-\cos (6t)\right)\) If desired, apply the negative angle identity
\(=\frac{1}{2} \left(\cos (2t)-\cos (6t)\right)\) Distribute
\(=\frac{1}{2} \cos (2t)-\frac{1}{2} \cos (6t)\)

Exercise

Evaluate \(\cos \left(\frac{11\pi }{12} \right)\cos \left(\frac{\pi }{12} \right)\).

Answer

\(\cos \left(\frac{11\pi }{12} \right)\cos \left(\frac{\pi }{12} \right)=\frac{1}{2} \left(\cos \left(\frac{11\pi }{12} +\frac{\pi }{12} \right)+\cos \left(\frac{11\pi }{12} -\frac{\pi }{12} \right)\right)\)
\(=\frac{1}{2} \left(\cos \left(\pi \right)+\cos \left(\frac{5\pi }{6} \right)\right)=\frac{1}{2} \left(-1-\frac{\sqrt{3} }{2} \right)\)
\(=\frac{-2-\sqrt{3} }{4}\)

IDENTITIES

The Sum-to-Product Identities

\(\sin \left(u\right)+\sin \left(v\right)=2\sin \left(\frac{u+v}{2} \right)\cos \left(\frac{u-v}{2} \right)\)
\(\sin \left(u\right)-\sin \left(v\right)=2\sin \left(\frac{u-v}{2} \right)\cos \left(\frac{u+v}{2} \right)\)
\(\cos \left(u\right)+\cos \left(v\right)=2\cos \left(\frac{u+v}{2} \right)\cos \left(\frac{u-v}{2} \right)\)
\(\cos \left(u\right)-\cos \left(v\right)=-2\sin \left(\frac{u+v}{2} \right)\sin \left(\frac{u-v}{2} \right)\)

We will again prove one of these and leave the rest as an exercise.

Proof of the sum-to-product identity for sine function

We define two new variables:

\(\begin{array}{l} {u=\alpha +\beta } \\ {v=\alpha -\beta } \end{array}\)

Adding these equations yields \(u+v=2\alpha\), giving \(\alpha =\frac{u+v}{2}\)

Subtracting the equations yields \(u-v=2\beta\), or \(\beta =\frac{u-v}{2}\)

Substituting these expressions into the product-to-sum identity

\(\sin (\alpha )\cos (\beta )=\frac{1}{2} \left(\sin (\alpha +\beta )+\sin (\alpha -\beta )\right)\) gives

\(\sin \left(\frac{u+v}{2} \right)\cos \left(\frac{u-v}{2} \right)=\frac{1}{2} \left(\sin \left(u\right)+\sin \left(v\right)\right)\) Multiply by 2 on both sides

\(2\sin \left(\frac{u+v}{2} \right)\cos \left(\frac{u-v}{2} \right)=\sin \left(u\right)+\sin \left(v\right)\) Establishing the identity

Exercise

Notice that, using the negative angle identity, \(\sin \left(u\right)-\sin \left(v\right)=\sin (u)+\sin (-v)\). Use this along with the sum of sines identity to prove the sum-to-product identity for \(\sin \left(u\right)-\sin \left(v\right)\).

Answer

\(\sin (u)-\sin (v)\) Use negative angle identity for sine
\(\sin (u) + \sin (-v)\) Use sum-to-product identity for sine
\(2\text{sin} (\dfrac{u + (-v)}{2}) \text{cos} (\dfrac{u - (-v)}{2})\) Eliminate the parenthesis
\(2\text{sin} (\dfrac{u - v}{2}) \text{cos} (\dfrac{u + v}{2})\) Establishing the identity

EXAMPLE 9

Evaluate \(\cos (15{}^\circ )-\cos (75{}^\circ )\).

Solution

Using the sum-to-product identity for the difference of cosines,

\(\cos (15{}^\circ )-\cos (75{}^\circ )\)
\(=-2\sin \left(\frac{15{}^\circ +75{}^\circ }{2} \right)\sin \left(\frac{15{}^\circ -75{}^\circ }{2} \right)\) Simplify
\(=-2\sin \left(45{}^\circ \right)\sin \left(-30{}^\circ \right)\) Evaluate
\(=-2\cdot \frac{\sqrt{2} }{2} \cdot \frac{-1}{2} =\frac{\sqrt{2} }{2}\)

EXAMPLE 10

Prove the identity \(\frac{\cos (4t)-\cos (2t)}{\sin (4t)+\sin (2t)} =-\tan (t)\).

Solution

Since the left side seems more complicated, we can start there and simplify.

\(\frac{\cos (4t)-\cos (2t)}{\sin (4t)+\sin (2t)}\) Use the sum-to-product identities
\(=\frac{-2\sin \left(\frac{4t+2t}{2} \right)\sin \left(\frac{4t-2t}{2} \right)}{2\sin \left(\frac{4t+2t}{2} \right)\cos \left(\frac{4t-2t}{2} \right)}\) Simplify
\(=\frac{-2\sin \left(3t\right)\sin \left(t\right)}{2\sin \left(3t\right)\cos \left(t\right)}\) Simplify further
\(=\frac{-\sin \left(t\right)}{\cos \left(t\right)}\) Rewrite as a tangent
\(=-\tan (t)\) Establishing the identity

EXAMPLE 11

Solve \(\sin \left(\pi {\kern 1pt} t\right)+\sin \left(3\pi {\kern 1pt} t\right)=\cos (\pi {\kern 1pt} t)\) for all solutions with \(0\le t<2\).

Solution

In an equation like th is, it is not immediately obvious how to proceed. One option would be to combine the two sine functions on the left side of the equation. Another would be to move the cosine to the left side of the equation, and combine it with one of the sines. For no particularly good reason, we’ll begin by combining the sines on the left side of the equation and see how things work out.

\(\sin \left(\pi {\kern 1pt} t\right)+\sin \left(3\pi {\kern 1pt} t\right)=\cos (\pi {\kern 1pt} t)\) Apply the sum to product identity on the left
\(2\sin \left(\frac{\pi {\kern 1pt} t+3\pi {\kern 1pt} t}{2} \right)\cos \left(\frac{\pi {\kern 1pt} t-3\pi {\kern 1pt} t}{2} \right)=\cos (\pi {\kern 1pt} t)\) Simplify
\(2\sin \left(2\pi {\kern 1pt} t\right)\cos \left(-\pi {\kern 1pt} t\right)=\cos (\pi {\kern 1pt} t)\) Apply the negative angle identity
\(2\sin \left(2\pi {\kern 1pt} t\right)\cos \left(\pi {\kern 1pt} t\right)=\cos (\pi {\kern 1pt} t)\) Rearrange the equation to be 0 on one side
\(2\sin \left(2\pi {\kern 1pt} t\right)\cos \left(\pi {\kern 1pt} t\right)-\cos (\pi {\kern 1pt} t)=0\) Factor out the cosine
\(\cos \left(\pi {\kern 1pt} t\right)\left(2\sin \left(2\pi {\kern 1pt} t\right)-1\right)=0\)

Using the Zero Product Theorem we know that at least one of the two factors must be zero. The first factor, \(\cos \left(\pi {\kern 1pt} t\right)\), has period \(P=\frac{2\pi }{\pi } =2\), so the solution interval of \(0\le t<2\) represents one full cycle of this function.

\(\cos \left(\pi {\kern 1pt} t\right)=0\) Substitute \(u=\pi {\kern 1pt} t\)
\(\cos \left(u\right)=0\) On one cycle, this has solutions
\(u=\frac{\pi }{2}\) or \(u=\frac{3\pi }{2}\) Undo the substitution
\(\pi {\kern 1pt} t=\frac{\pi }{2}\), so \(t=\frac{1}{2}\)
\(\pi {\kern 1pt} t=\frac{3\pi }{2}\), so \(t=\frac{3}{2}\)

The second factor, \(2\sin \left(2\pi {\kern 1pt} t\right)-1\), has period of \(P=\frac{2\pi }{2\pi } =1\), so the solution interval \(0\le t<2\) contains two complete cycles of this function.

\(2\sin \left(2\pi {\kern 1pt} t\right)-1=0\) Isolate the sine
\(\sin \left(2\pi {\kern 1pt} t\right)=\frac{1}{2}\) Substitute \(u=2\pi {\kern 1pt} t\)
\(\sin (u)=\frac{1}{2}\) On one cycle, this has solutions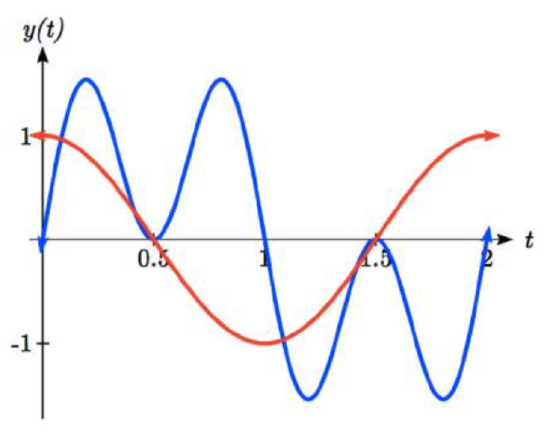
\(u=\frac{\pi }{6}\) or \(u=\frac{5\pi }{6}\) On the second cycle, the solutions are
\(u=2\pi +\frac{\pi }{6} =\frac{13\pi }{6}\) or \(u=2\pi +\frac{5\pi }{6} =\frac{17\pi }{6}\) Undo the substitution
\(2\pi {\kern 1pt} t=\frac{\pi }{6}\), so \(t=\frac{1}{12}\)
\(2\pi {\kern 1pt} t=\frac{5\pi }{6}\), so \(t=\frac{5}{12}\)
\(2\pi {\kern 1pt} t=\frac{13\pi }{6}\), so \(t=\frac{13}{12}\)
\(2\pi {\kern 1pt} t=\frac{17\pi }{6}\), so \(t=\frac{17}{12}\)

Altogether, we found six solutions on \(0\le t<2\), which we can confirm by looking at the graph.

\(t=\frac{1}{12} ,\frac{5}{12} ,\frac{1}{2} ,\frac{13}{12} ,\frac{3}{2} ,\frac{17}{12}\)

Important Topics of This Section

• The sum and difference identities
• Combining waves of equal periods
• Product-to-sum identities
• Sum-to-product identities
• Completing proofs