8.4.1: Vectors (Exercise)
- Page ID
- 22245
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)section 8.4 exercises
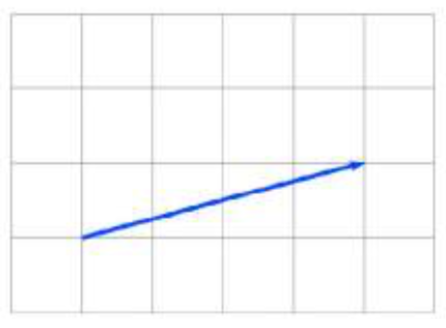
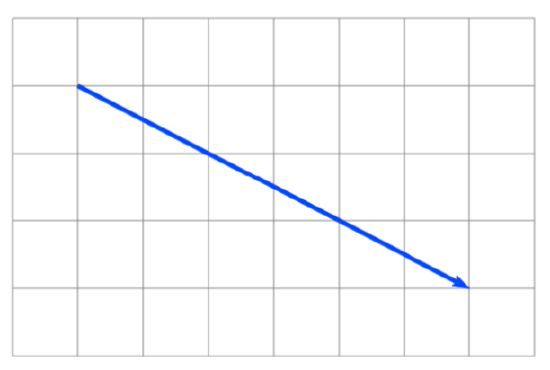
Write the vector shown in component form.
1. 
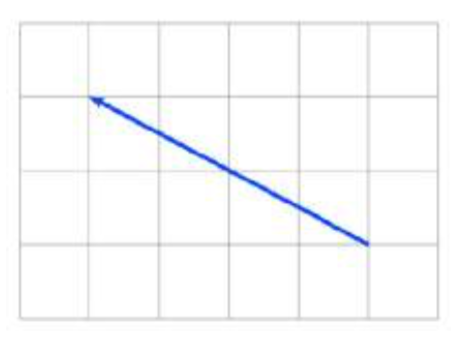2. 
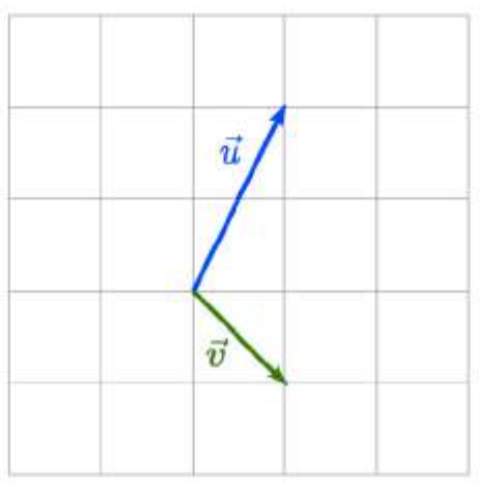
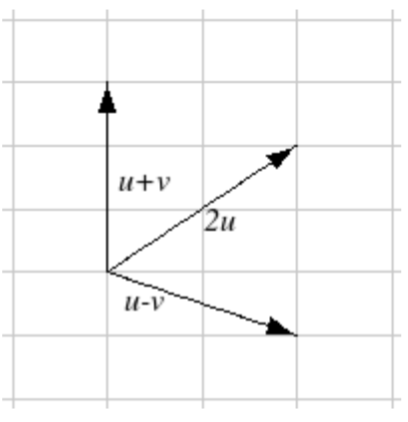
Given the vectors shown, sketch \(\vec{u} + \vec{v}\), \(\vec{u} - \vec{v}\), and \(2\vec{u}\).
3. 
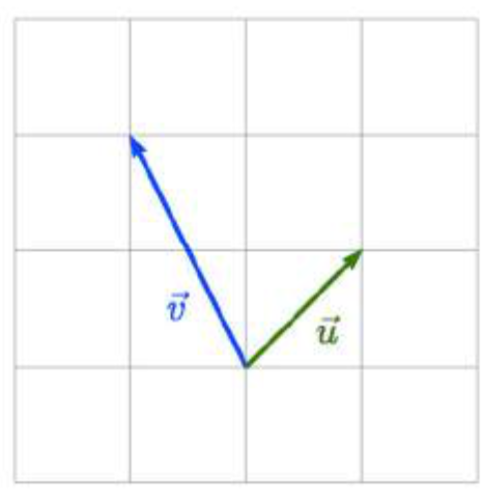4. 
Write each vector below as a combination of the vectors \(\vec{u}\) and \(\vec{v}\) from question #3.
5. 
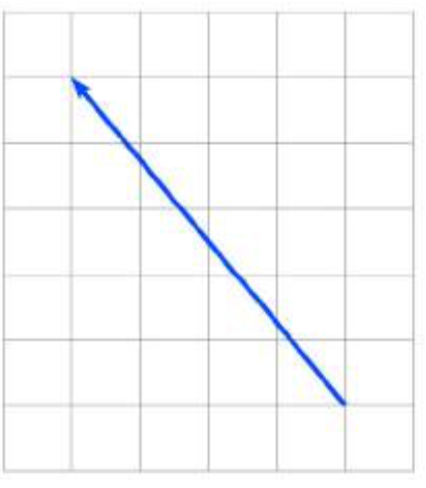6. 
From the given magnitude and direction in standard position, write the vector in component form.
7. Magnitude: 6, Direction: \(45^{\circ}\)
8. Magnitude: 10, Direction: \(120^{\circ}\)
9. Magnitude: 8, Direction: \(220^{\circ}\)
10. Magnitude: 7, Direction: \(305^{\circ}\)
Find the magnitude and direction of the vector.
11. \(\langle 0, 4 \rangle\)
12. \(\langle -3, 0 \rangle\)
13. \(\langle 6, 5 \rangle\)
14. \(\langle 3, 7 \rangle\)
15. \(\langle -2, 1 \rangle\)
16. \(\langle -10, 13 \rangle\)
17. \(\langle 2, -5 \rangle\)
18. \(\langle 8, -4 \rangle\)
19. \(\langle -4, -6 \rangle\)
20. \(\langle -1, 9 \rangle\)
Using the vectors given, compute \(\vec{u} + \vec{c}\), \(\vec{u} - \vec{c}\), and \(2\vec{u} - 3\vec{c}\).
21. \(\vec{u} = \langle 2, -3 \rangle, \vec{v} = \langle 1, 5 \rangle\)
22. \(\vec{u} = \langle -3, 4 \rangle, \vec{v} = \langle -2, 1 \rangle\)
23. A woman leaves home and walks 3 miles west, then 2 miles southwest. How far from home is she, and in what direction must she walk to head directly home?
24. A boat leaves the marina and sails 6 miles north, then 2 miles northeast. How far from the marina is the boat, and in what direction must it sail to head directly back to the marina?
25. A person starts walking from home and walks 4 miles east, 2 miles southeast, 5 miles south, 4 miles southwest, and 2 miles east. How far have they walked? If they walked straight home, how far would they have to walk?
26. A person starts walking from home and walks 4 miles east, 7 miles southeast, 6 miles south, 5 miles southwest, and 3 miles east. How far have they walked? If they walked straight home, how far would they have to walk?
27. Three forces act on an object: \(\vec{F}_1 = \langle -8, -5 \rangle\), \(\vec{F}_2 = \langle 0, 1 \rangle\), \(\vec{F}_3 = \langle 4, -7 \rangle\). Find the net force acting on the object.
28. Three forces act on an object: \(\vec{F}_1 = \langle 2, 5 \rangle\), \(\vec{F}_2 = \langle 8, 3 \rangle\), \(\vec{F}_3 = \langle 0, -7 \rangle\). Find the net force acting on the object.
29. A person starts walking from home and walks 3 miles at \(20^{\circ}\) north of west, then 5 miles at 10° west of south, then 4 miles at \(15^{\circ}\) north of east. If they walked straight home, how far would they have to walk, and in what direction?
30. A person starts walking from home and walks 6 miles at 40° north of east, then 2 miles at \(15^{\circ}\) east of south, then 5 miles at \(30^{\circ}\) south of west. If they walked straight home, how far would they have to walk, and in what direction?
31. An airplane is heading north at an airspeed of 600 km/hr, but there is a wind blowing from the southwest at 80 km/hr. How many degrees off course will the plane end up flying, and what is the plane’s speed relative to the ground?
32. An airplane is heading north at an airspeed of 500 km/hr, but there is a wind blowing from the northwest at 50 km/hr. How many degrees off course will the plane end up flying, and what is the plane’s speed relative to the ground?
33. An airplane needs to head due north, but there is a wind blowing from the southwest at 60 km/hr. The plane flies with an airspeed of 550 km/hr. To end up flying due north, the pilot will need to fly the plane how many degrees west of north?
34. An airplane needs to head due north, but there is a wind blowing from the northwest at 80 km/hr. The plane flies with an airspeed of 500 km/hr. To end up flying due north, the pilot will need to fly the plane how many degrees west of north?
35. As part of a video game, the point (5, 7) is rotated counterclockwise about the origin through an angle of 35 degrees. Find the new coordinates of this point.
36. As part of a video game, the point (7, 3) is rotated counterclockwise about the origin through an angle of 40 degrees. Find the new coordinates of this point.
37. Two children are throwing a ball back and forth straight across the back seat of a car. The ball is being thrown 10 mph relative to the car, and the car is travelling 25 mph down the road. If one child doesn't catch the ball and it flies out the window, in what direction does the ball fly (ignoring wind resistance)?
38. Two children are throwing a ball back and forth straight across the back seat of a car. The ball is being thrown 8 mph relative to the car, and the car is travelling 45 mph down the road. If one child doesn't catch the ball and it flies out the window, in what direction does the ball fly (ignoring wind resistance)?
- Answer
-
1. -4, 2
3.
The vectors do not need to start at the same point5. \(3\bar{v} - \bar{u}\)
7. \(3\sqrt{2}, 3\sqrt{2}\)
9. −6.128, −5.142
11. Magnitude: 4, Direction: \(90^{\circ}\)
13. Magnitude: 7.810, Direction: \(39.806^{\circ}\)
15. Magnitude: 2.236, Direction: \(153.435^{\circ}\)
17. Magnitude: 5.385, Direction: \(291.801^{\circ}\)
19. Magnitude: 7.211, Direction: \(236.310^{\circ}\)
21. \(\bar{u} + \bar{v} = \langle 3, 2 \rangle, \bar{u} - \bar{v} = \langle 1, -8 \rangle, 2\bar{u} - 3\bar{v} = \langle 1, -21 \rangle\)
23. 4.635 miles, 17.764 deg N of E
25. 17 miles. 10.318 miles
27. \(\overrightarrow{F_{net}} = -4, -11\)
29. Distance: 2.868. Direction: \(86.474^{\circ}\) North of West, or \(3.526^{\circ}\) West of North
31. 4.924 degrees. 659 km/hr
33. 4.424 degrees
35. (0.081, 8.602)
37. 21.801 degrees, relative to the car’s forward direction