3.1: Trigonometric Functions of Angles
( \newcommand{\kernel}{\mathrm{null}\,}\)
Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- How do we define the cosine and sine as functions of angles?
- How are the trigonometric functions defined on angles using circles of any radius?
Beginning Activity
- How do we define an angle whose measure is one radian? See the definition on page 27.
- Draw an angle in standard position with a measure of π4 radians. Draw an angle in standard position with a measure of 5π3 radians.
- What is the formula for the arc length s on a circle of radius r that is intercepted by an angle with radian measure θ? See page 36. Why does this formula imply that radians are a dimensionless quantity and that a measurement in radians can be thought of as a real number?
Some Previous Results
In Section 1.2, we defined the cosine function and the sine function using the unit circle. In particular, we learned that we could define cos(t) and sin(t) for any real number where the real number t could be thought of as the length of an arc on the unit circle.
In Section 1.3, we learned that the radian measure of an angle is the length of the arc on the unit circle that is intercepted by the angle. That is,
An angle (in standard position) of t radians will correspond to an arc of length t on the unit circle, and this allows us to think of cos(t) and sin(t) when t is the radian measure of an angle.
So when we think of cos(t) and sin(t) (and the other trigonometric functions), we can consider t to be:
- a real number;
- the length of an arc with initial point (1,0) on the unit circle;
- the radian measure of an angle in standard position.
Figure 3.1.1 shows an arc on the unit circle with the corresponding angle.
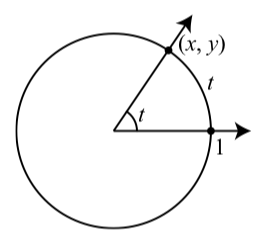
Figure 3.1.1: An Angle in Standard Position with the Unit Circle
Trigonometric Functions of an Angle
With the notation in Figure 3.1, we see that cos(t)=x and sin(t)=y. In this context, we often the cosine and sine circular functions because they are defined by points on the unit circle. Now we want to focus on the perspective the cosine and sine as functions of angles. When using this perspective we will refer to the cosine and sine as trigonometric functions. Technically, we have two different types of cosines and sines: one defined as functions of arcs and the other as functions of angles. However, the connection is so close and the distinction so minor that we will often interchange the terms circular and trigonometric. One notational item is that when we think of the trigonometric functions as functions of angles, we often use Greek letters for the angles. The most common ones are θ(theta), α(alpha), β(beta), and ϕ(phi).
Although the definition of the trigonometric functions uses the unit circle, it will be quite useful to expand this idea to allow us to determine the cosine and sine of angles related to circles of any radius. The main concept we will use to do this will be similar triangles. We will use the triangles shown in Figure 3.2.
In this figure, the angle θ is in standard position, the point P(u,v) is on the unit circle, and the point Q is on a circle of radius r. So we see that cos(θ)=u and sin(θ)=v
We will now use the triangles △PAO and △PAO to write cos(θ) and sin(θ) terms of x,y, and r. Figure 3.3 shows these triangles by themselves without the circles.
The two triangles in Figure 3.2 are similar triangles since the corresponding angles of the two triangles are equal. (See page 421 in Appendix C.) Because of this, we can write u1=xr u=xr cos(θ)=xr and u1=yr v=yr sin(θ)=yr
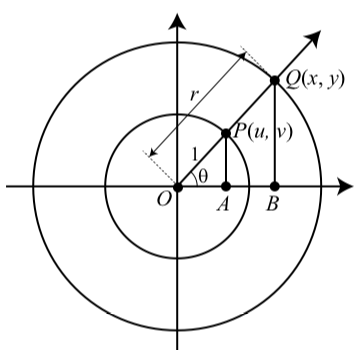
Figure 3.1.2: An Angle in Standard Position
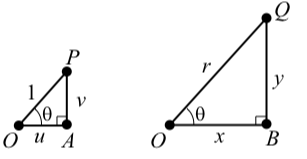
Figure 3.1.3: Similar Triangles from Figure 3.1.2
In addition, note that u2+v2=1 and x2+y2=r2. So we have obtained the following results, which show that once we know the coordinates of one point on the terminal side of an angle θ in standard position, we can determine all six trigonometric functions of that angle.
For any point (x,y) other than the origin on the terminal side of an angle θ in standard position, the trigonometric functions of θ are defined as: cos(θ)=xr sin(θ)=yr tan(θ)=yx,x≠0 sec(θ)=rx,x≠0 csc(θ)=ry,y≠0 cot(θ)=xy,y≠0 where r2=x2+y2 and r>0 and so r=√x2+y2.
Notice that the other trigonometric functions can also be determined in terms of x,y, and r. For example, if x≠0, then tan(θ)=sin(θ)cos(θ)=yrxr=yr⋅rx=yx sec(θ)=1cos(θ)=1xr=1⋅rx=rx
For example, if the point (3,−1) is on the terminal side of the angle θ, then we can use x=3, y=−1, and r=√(−3)2+12=√10, and so
cos(θ)=3√10 sin(θ)=−1√10 tan(θ)=−13 cot(θ)=−31 sec(θ)=√103 csc(θ)=−√101
The next two exercises will provide some practice with using these results.
Exercise 3.1.1
Suppose we know that the point P(3,7) is on the terminal side of the angle θ in standard position.
- Draw a coordinate system, plot the point P, and draw the terminal side of the angle θ.
- Determine the radius r of the circle centered at the origin that passes through the point P(−5,13). Hint: x2+y2=r2.
- Now determine the values of the six trigonometric functions of θ.
- Answer
-
1.
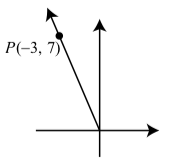
2. r=√(−3)2+72=√58
3. cos(θ)=−3√58
sin(θ)=7√58
tan(θ)=−73
cos(θ)=−37
sec(θ)=−√583
tan(θ)=√587
Exercise 3.1.2
Suppose that α is an angle, that tan(α)=23, and when α is in standard position, its terminal side is in the third quadrant.
- Draw a coordinate system, draw the terminal side of the angle α in standard position.
- Determine a point that lies on the terminal side of α.
- Determine the six trigonometric functions of α.
- Answer
-
1.
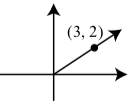
2. Since tan(α)=23, we can conclude that the point (3,2) lies on the terminal side of α.
3. Since (3,2) is on the terminal side of α we can use x=3,y=2, and r=√32+22. So
cos(θ)=2√13
sin(θ)=3√13
tan(θ)=23
cos(θ)=32
sec(θ)=−√132
tan(θ)=√133
The Pythagorean Identity
Perhaps the most important identity for the circular functions is the so-called Pythagorean Identity, which states that for any real number t, cos2(t)+sin2(t)=1
It should not be surprising that this identity also holds for the trigonometric functions when we consider these to be functions of angles. This will be verified in the next progress check.
Exercise 3.1.3
Let θ be an angle and assume that (x,y) is a point on the terminal side of θ in standard position. We then let r2=x2+y2. So we see that cos(θ)2+cos(θ)2=(xr)2+(yr)2.
- Use algebra to rewrite (xr)2+(yr)2 as a single fraction with denominator its terminal side is in the third quadrant.
- Now use the fact that x2+y2=r2 to prove that (xr)2+(yr)2=1
- Finally, conclude that cos(θ)2+sin(θ)2=1
- Answer
-
The completed work should look something like the following:
cos2(θ)+sin2(θ)=(xr)2+(yr)2=x2r2+y2r2=x2+y2r2=r2r2=1
The next progress check shows how to use the Pythagorean Identity to help determine the trigonometric functions of an angle.
Exercise 3.1.4
Assume that θ is an angle in standard position and that sin(θ)=13 and π2<θ<π.
- Use the Pythagorean Identity to determine cos2(θ) and then use the fact that π2<θ<π to determine cos(θ).
- Use the identity tan(θ)=sin(θ)cos(θ) to determine the value of tan(θ).
- Determine the values of the other three trigonometric functions of θ.
- Answer
-
1. Using the Pythagorean Identity, we see that cos2(θ)+(13)2=1 and so cos2(θ)=89. Since π2<θ<π, cos(θ)<0. Hence, cos(θ)=−√83.
2. tan(θ)=13−√83=−1√8.
3. cot(θ)=−√8,csc(θ)=3, and sec(θ)=−3√8
The Inverse Trigonometric Functions
In Section 2.5, we studied the inverse trigonometric functions when we considered the trigonometric (circular) functions to be functions of a real number t. At the start of this section, however, we saw that t could also be considered to be the length of an arc on the unit circle, or the radian measure of an angle in standard position. At that time, we were using the unit circle to determine the radian measure of an angle but now we can use any point on the terminal side of the angle to determine the angle. The important thing is that these are now functions of angles and so we can use the inverse trigonometric functions to determine angles. We can use either radian measure or degree measure for the angles. The results we need are summarized below.
- θ=arcsin(x)=sin−1(x) means sin(θ)=x and −π2≤θ≤π2 or −90∘≤θ≤90∘.
- θ=arccos(x)=cos−1(x) means cos(θ)=x and 0≤θ≤π or 0∘≤θ≤180∘.
- θ=arctan(x)=tan−1(x) means tan(θ)=x and −π2<θ<π2 or −90∘<θ<90∘.
The important things to remember are that an equation involving the inverse trigonometric function can be translated to an equation involving the corresponding trigonometric function and that the angle must be in a certain range. For example, if we know that the point (5,3) is on the terminal side of an angle θ and that 0≤θ<π, then we know that tan(θ)=yx=35
We can use the inverse tangent function to determine (and approximate) the angle since the inverse tangent function gives an angle (in radian measure) between −π2 and π2. Since tan(θ)>0, we will get an angle between 0 and π2. θ=arctan(35)≈0.54042
If we used degree measure, we would get π2. θ=arctan(35)≈30.96376∘
It is important to note that in using the inverse trigonometric functions, we must be careful with the restrictions on the angles. For example, if we had stated that tan(α)=53 and π<α<3π2, then the inverse tangent function would not give the correct result. We could still use θ=arctan(35)≈0.54042 but now we would have to use this result and the fact that the terminal side of α is in the third quadrant. So α=θ+π α=arctan(35)+π α≈3.68201
We should now use a calculator to verify that tan(α)=35
The relationship between the angles α and θ is shown in Figure 3.1.4.
Exercise 3.1.1
Suppose that the point (−2,5) is on the terminal side of the angle θ in standard position and that 0≤θ<360∘. We then know that tan(θ)=−52=−2.5.
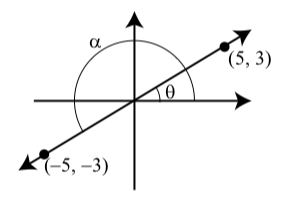
Figure 3.1.4: Two Angles with the Same Tangent Value
- Draw a picture of the angle θ.
- Use a calculator to approximate the value of tan−1(−2.5) to three decimal places.
- Notice that tan−1(−2.5) is a negative angle and cannot equal θ since θ is a positive angle. Use the approximation for tan−1(−2.5) to determine an approximation for θ to three decimal places.
- Answer
-
2. tan−1(−2.5)≈−68.199∘
3. θ=−68.199∘+180∘≈111.801∘
In the following example, we will determine the exact value of an angle that is given in terms of an inverse trigonometric function.
Example 3.1.1: Determining an Exact Value
We will determine the exact value of cos(arcsin(−27)). Notice that we can use a calculator to determine that cos(arcsin(−27))≈0.958315
Even though this is correct to six decimal places, it is not the exact value. We can use this approximation, however, to check our work below.
We let θ=arcsin(−27) We then know that sin(θ)=−27 and −π2≤θ≤π2
We note that since sin(θ)<0, we actually know that −π2≤θ≤0.
So we can use the Pythagorean Identity to determine cos2(θ) as follows: cos2(θ)+sin2(θ)=1 cos2(θ)=1−(−27)2 cos2(θ)=4549
Since −π2≤θ≤0, we see that cos(θ)=√457. That is cos(arcsin(−27))=√457.
We can now use a calculator to verify that √457≈0.958315.
Summary
In this section, we studied the following important concepts and ideas:
The trigonometric functions can be defined using any point on the terminal side of an angle in standard position. For any point (x,y) other than the origin on the terminal side of an angle θ in standard position, the trigonometric functions of θ are defined as:
cos(θ)=xr sin(θ)=yr tan(θ)=yx,x≠0 sec(θ)=rx,x≠0 csc(θ)=ry,y≠0 cot(θ)=xy,y≠0 where r2=x2+y2 and r>0 and so r=√x2+y2. ThePythagoreanIdentity is still true when we use the trigonometric functions of an angle. That is, for any angle, cos(θ)2+sin(θ)2=1.
In addition, we still have the inverse trigonometric functions. In particular,
- θ=arcsin(x)=sin−1(x) means sin(θ)=x and −π2≤θ≤π2 or −90∘≤θ≤90∘.
- θ=arccos(x)=cos−1(x) means cos(θ)=x and 0≤θ≤π or 0∘≤θ≤180∘.
- θ=arctan(x)=tan−1(x) means tan(θ)=x and −π2<θ<π2 or −90∘<θ<90∘.


