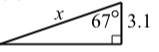3.E: Triangles and Vectors (Exercises)

Last updated

Jan 2, 2021
Save as PDF
- 3.6: Vectors from an Algebraic Point of View
- 4: Trigonometric Identities and Equations

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Exercise $\PageIndex{1}$

In each of the following, the coordinates of a point $P$ on the terminal side of an angle $\theta$ are given. For each of the following:

Plot the point $P$ in a coordinate system and draw the terminal side of the angle.

Determine the radius $r$ of the circle centered at the origin that passes through the point $P$ .

Determine the values of the six trigonometric functions of the angle $\theta$ .

$P(3, 3)$
$P(5, 8)$
$P(-2, -2)$
$P(5, -2)$
$P(-1, -4)$
$P(2\sqrt{3}, 2)$
$P(-3, 4)$
$P(3, -3\sqrt{3})$
$P(2, -1)$

Answer

(a) We see that $r = \sqrt{3^{2} + 3^{2}} = \sqrt{18}$ . So

$\cos(\theta) = \dfrac{3}{\sqrt{18}} = \dfrac{3}{3\sqrt{2}} = \dfrac{1}{\sqrt{2}}$

$\tan(\theta) = \dfrac{3}{3} = 1$

$\sec(\theta) = \dfrac{\sqrt{18}}{3} = \sqrt{2}$

$\sin(\theta) = \dfrac{3}{\sqrt{18}} = \dfrac{3}{3\sqrt{2}} = \dfrac{1}{\sqrt{2}}$

$\cot(\theta) = \dfrac{3}{3} = 1$

$\csc(\theta) = \dfrac{\sqrt{18}}{3} = \sqrt{2}$

(b)

We see that $r = \sqrt{5^{2} + 8^{2}} = \sqrt{89}$ . So

$\cos(\theta) = \dfrac{5}{\sqrt{89}}$

$\tan(\theta) = \dfrac{8}{5}$

$\sec(\theta) = \dfrac{\sqrt{89}}{5}$

$\sin(\theta) = \dfrac{8}{\sqrt{89}}$

$\cot(\theta) = \dfrac{5}{8} = 1$

$\csc(\theta) = \dfrac{\sqrt{89}}{8}$

(e)

We see that $r = \sqrt{(-1)^{2} + (-4)^{2}} = \sqrt{26}$ . So

$\cos(\theta) = \dfrac{-3}{\sqrt{26}}$

$\tan(\theta) = 4$

$\sec(\theta) = -\dfrac{\sqrt{26}}{4}$

$\sin(\theta) = \dfrac{-3}{\sqrt{26}}$

$\cot(\theta) = \dfrac{1}{4} = 1$

$\csc(\theta) = -\sqrt{26}$

Exercise $\PageIndex{2}$

For each of the following, draw the terminal side of the indicated angle on a coordinate system and determine the values of the six trigonometric functions of that angle

The terminal side of the angle $\alpha$ is in the first quadrant and $\sin(\alpha) = \dfrac{1}{\sqrt{3}}$
The terminal side of the angle $\beta$ is in the second quadrant and $\cos(\beta) = -\dfrac{2}{3}$
The terminal side of the angle $\gamma$ is in the second quadrant and $\tan(\gamma) = -\dfrac{1}{2}$
The terminal side of the angle $\theta$ is in the second quadrant and $\sin(\theta) = \dfrac{1}{3}$

Answer

2. We first use the Pythagorean Identity and obtain $\sin^{2}(\beta) = \dfrac{5}{9}$ . Since the terminal side of $\beta$ is in the second quadrant, $\sin(\beta) = \dfrac{\sqrt{5}}{3}$ . In addition,

$\tan(\beta) = -\dfrac{\sqrt{5}}{2}$

$\cot(\beta) = -\dfrac{2}{\sqrt{5}}$

$\sec(\beta) = -\dfrac{3}{2}$

$\csc(\beta) = \dfrac{3}{\sqrt{5}}$

Exercise $\PageIndex{3}$

For each of the following, determine an approximation for the angle $\theta$ in degrees (to three decimal places) when $0^\circ \leq \theta \leq 360^\circ$ .

The point $(3, 5)$ is on the terminal side of $\theta$ .
The point $(2, -4)$ is on the terminal side of $\theta$ .
$\sin(\theta) = \dfrac{2}{3}$ and the terminal side of $\theta$ is in the second quadrant.
$\sin(\theta) = -\dfrac{2}{3}$ and the terminal side of $\theta$ is in the fourth quadrant.
$\cos(\theta) = -\dfrac{1}{4}$ and the terminal side of $\theta$ is in the second quadrant.
$\cos(\theta) = -\dfrac{3}{4}$ and the terminal side of $\theta$ is in the third quadrant.

Answer

3. Since the terminal side of $\theta$ is in the second quadrant, $\theta$ is not the inverse sine of $\dfrac{2}{3}$ . So we let $\alpha = \arcsin(\dfrac{2}{3})$ . Using $\alpha$ as the reference angle, we then see that $\theta = 180^\circ - \arcsin(\dfrac{2}{3}) \approx 138.190^\circ$

5. $\theta = \arccos(-\dfrac{1}{4}) \approx 104.478^\circ$ , or use \(\alpha\ = \arccos(\dfrac{1}{4})) for the reference angle.

$\theta = 180^\circ - \arccos(\dfrac{1}{4}) \approx 104.478^\circ.$

Exercise $\PageIndex{4}$

For each of the angles in Exercise (3), determine the radian measure of $\theta$ if $0 \leq \theta \leq 2\pi$ .

Answer

3. $\theta = \pi - \arcsin(\dfrac{2}{3}) \approx 2.142.$

5. $\theta = \pi - \arccos(\dfrac{1}{4}) \approx 1.823.$

Exercise $\PageIndex{5}$

Determine the exact value of each of the following. Check all results with a calculator.

$\cos(\arcsin(\dfrac{1}{5}))$
$\tan(\cos^{-1}(\dfrac{2}{3}))$
$\sin(\tan^{-1}(2))$
$\cos(\arcsin(-\dfrac{1}{5}))$
$\sin(\arccos(-\dfrac{3}{5}))$

Answer

2. Let $\theta = \cos^{-1}(\dfrac{2}{3})$ . Then $\cos(\theta) = \dfrac{2}{3}$ and $0 \leq \theta \leq \pi$ . So $\sin(\theta) > 0$ and $\sin^{2}(\theta) = 1 - \cos^{2}(\theta) = \dfrac{5}{9}$ . So

$\tan(\cos^{-1}(\dfrac{2}{3})) = \tan(\theta) = \dfrac{\sin(\theta)}{\cos(\theta)} = \dfrac{\dfrac{\sqrt{5}}{3}}{\dfrac{2}{3}} = \dfrac{\sqrt{5}}{2}$

Using a calculator, we obtain

$\tan(\cos^{-1}(\dfrac{2}{3})) \approx 1.11803$ and $\dfrac{\sqrt{5}}{2} \approx 1.11803$

Exercise $\PageIndex{6}$

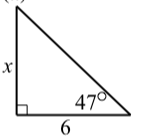
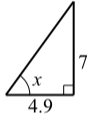
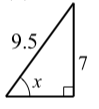
For each of the following right triangles, determine the value of $x$ correct to the nearest thousandth.

$e1a.png$
$e2b.png$
$e2c.png$
$e2d.png$

Answer

$x = 6\tan(47^\circ) \approx 6.434$ .
$x = 3.1\cos(67^\circ) \approx 1.211$ .
$x = \tan^{-1}(\dfrac{7}{4.9}) \approx 55.008^\circ$ .
$x = \sin^{-1}(\dfrac{7}{9.5}) \approx 47.463^\circ$ .

Exercise $\PageIndex{7}$

One angle in a right triangle is $55^\circ$ and the side opposite that angle is 10 feet long. Determine the length of the other side, the length of the hypotenuse, and the measure of the other acute angle.

Exercise $\PageIndex{8}$

One angle in a right triangle is $37.8^\circ$ and the length of the hypotenuse is 25 inches. Determine the length of the other two sides of the right triangle.

Exercise $\PageIndex{9}$

One angle in a right triangle is $27^\circ 12'$ and the length of the side adjacent to this angle is 4 feet. Determine the other acute angle in the triangle, the length of the side opposite this angle, and the length of the hypotenuse.
Note: The notation means that the angle is 27 degrees, 12 seconds. Remember that 1 second is $\dfrac{1}{60}$ of a degree.

Answer: The other acute angle is $64^\circ 48'$ .
The side opposite the $27^\circ 12'$ angle is $4\tan(27^\circ 12') \approx 2.056$ feet.; The hypotenuse is $\dfrac{4}{\cos(27^\circ 12')} \approx 4.497$ feet.
Note that the Pythagorean Theorem can be used to check the results by showing that $4^{2} + 2.056^{2} \approx 4.497^{2}$ . The check will not be exact because the $2.056$ and $4.497$ are approximations of the exact values.

Exercise $\PageIndex{10}$

If we only know the measures of the three angles of a right triangle, ex- plain why it is not possible to determine the lengths of the sides of this right triangle.

Exercise $\PageIndex{11}$

Suppose that we know the measure $\theta$ of one of the acute angles in a right triangle and we know the length $x$ of the side opposite the angle $\theta$ . Explain how to determine the length of the side adjacent to the angle $\theta$ and the length of the hypotenuse.

Exercise $\PageIndex{12}$

In the diagram to the right, determine the values of $a$ , $b$ , and $h$ to the nearest thousandth.
The given values are:

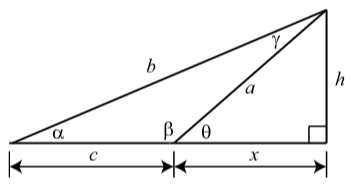
$e7.png$

Figure $\PageIndex{1}$

$\alpha = 23^\circ$

$\beta = 140^\circ$

$c = 8$

Answer

We first note that $\theta = 40^\circ$ . We use the following two equations to determine $x$ .

$\tan(\alpha) = \dfrac{h}{c + x}$ $\tan(x) = \dfrac{h}{x}$

Substituting $h = x\tan(\theta)$ into the first equation and solving for $x$ gives $x = \dfrac{c\tan(\alpha)}{\tan(\theta) - \tan(\alpha)} \approx 8.190.$

We can then use right triangles to obtain $h \approx 6.872\space ft, a \approx 10.691\space ft, and b \approx 17.588\space ft$

Exercise $\PageIndex{13}$

A tall evergreen tree has been damaged in a strong wind. The top of the tree is cracked and bent over, touching the ground as if the trunk were hinged. The tip of the tree touches the ground 20 feet 6 inches from the base of the tree (where the tree and the ground meet). The tip of the tree forms an angle of 17 degrees where it touches the ground. Determine the original height of the tree (before it broke) to the nearest tenth of a foot. Assume the base of the tree is perpendicular to the ground.

Exercise $\PageIndex{14}$

Suppose a person is standing on the top of a building and that she has an instrument that allows her to measure angles of depression. There are two points that are 100 feet apart and lie on a straight line that is perpendicular to the base of the building.

Now suppose that she measures the angle of depression to the closest point to be $35.5^\circ$ and that she measures the angle of depression to the other point to be $29.8^\circ$ . Determine the height of the building. $page206image32203024$

Exercise $\PageIndex{15}$

A company has a 35 foot ladder that it uses for cleaning the windows in their building. For safety reasons, the ladder must never make an angle of more than $50^\circ$ with the ground.

What is the greatest height that the ladder can reach on the building if the angle it makes with the ground is no more than $50^\circ$ .
Suppose the building is 40 feet high. Again, following the safety guidelines, what length of ladder is needed in order to have the ladder reach the top of the building?

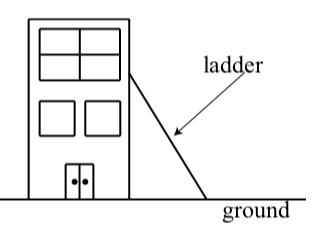
$e10.png$

Figure $\PageIndex{2}$

Note

For Exercises $\PageIndex{16}$ through $\PageIndex{19}$ , use the Law of Sines.

Exercise $\PageIndex{16}$

Two angles of a triangle are $42^\circ$ and $73^\circ$ . The side opposite the $73^\circ$ angle is 6.5 feet long. Determine the third angle of the triangle and the lengths of the other two sides.

Answer: The third angle is $65^\circ$ . The side opposite the $42^\circ$ angle is $4.548$ feet long. The side opposite the $65^\circ$ angle is $6.160$ feet long.

Exercise $\PageIndex{17}$

A triangle has a side that is 4.5 meters long and this side is adjacent to an angle of $110^\circ$ . In addition, the side opposite the $110^\circ$ angle is 8 meters long. Determine the other two angles of the triangle and the length of the third side.

Exercise $\PageIndex{18}$

A triangle has a side that is 5 inches long that is adjacent to an angle of $61^\circ$ . The side opposite the $61^\circ$ angle is 4.5 inches long. Determine the other two angles of the triangle and the length of the third side.

Answer: There are two triangles that satisfy these conditions. The sine of the angle opposite the $5$ inch side is approximately $0.9717997$ .

Exercise $\PageIndex{19}$

In a given triangle, the side opposite an angle of $107^\circ$ is 18 inches long. One of the sides adjacent to the $107^\circ$ angle is 15.5 inches long. Determine the other two angles of the triangle and the length of the third side.

Note

For Exercises $\PageIndex{20}$ through $\PageIndex{21}$ , use the Law of Cosines.

Exercise $\PageIndex{20}$

The three sides of a triangle are 9 feet long, 5 feet long, and 7 feet long. Determine the three angles of the triangle.

Answer: The angle opposite the $9$ foot long side is $95.739^\circ$ . The angle opposite the $7$ foot long side is $50.704^\circ$ . The angle opposite the $5$ foot long side is $33.557^\circ$ .

Exercise $\PageIndex{21}$

A triangle has two sides of lengths 8.5 meters and 6.8 meters. The angle formed by these two sides is $102^\circ$ . Determine the length of the third side and the other two angles of the triangle

Note

For the remaining exercises, use an appropriate method to solve the problem.

Exercise $\PageIndex{22}$

Two angles of a triangle are $81.5^\circ$ and $34^\circ$ . The length of the side opposite the third angle is 8.8 feet. Determine the third angle and the lengths of the other two sides of the triangle.

Exercise $\PageIndex{23}$

In the diagram below, determine the value of $\gamma$ (to the nearest hundredth of a degree) and determine the values of $h$ and $d$ (to the nearest thousandth) if it is given that $a = 4$ $b = 8$ $c = 10$ $\theta = 26^\circ$

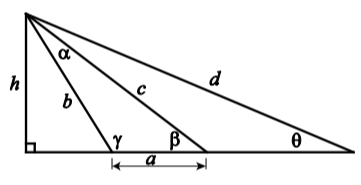
$e8.png$

Figure $\PageIndex{3}$

Exercise $\PageIndex{24}$

In the diagram below, it is given that:

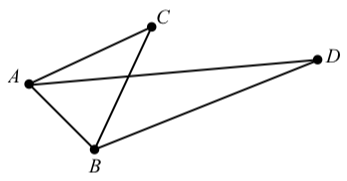
$e9.png$

Figure $\PageIndex{4}$

The length of $AC$ is $2$ .
The length of $BC$ is $2$ .
$\angle ACB = 40^\circ$
$\angle CAD = 20^\circ$
$\angle CBD = 45^\circ$

Determine the lengths of $AB$ and $AD$ to the nearest thousandth.

Exercise $\PageIndex{25}$

A ski lift is to be built along the side of a mountain from point $A$ to point $B$ in the following diagram. We wish to determine the length of this ski lift.

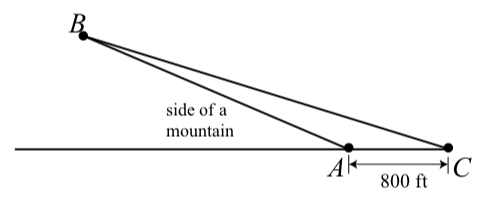
$e1.png$

Figure $\PageIndex{5}$

A surveyor determines the measurement of angle $BAC$ to be $155.6^\circ$ and then measures a distance of 800 ft from Point $A$ to Point $C$ . Finally, she determines the measurement of angle $BCA$ to be $17.2^\circ$ . What is the the length of the ski lift (from point $A$ to point $B$ )?

Answer: The ski lift is about $1887.50$ feet long.

Exercise $\PageIndex{26}$

A boat sails from Muskegon bound for Chicago, a sailing distance of 121 miles. The boat maintains a constant speed of 15 miles per hour. After encountering high cross winds the crew finds itself off course by $20^\circ$ after 4 hours. A crude picture is shown in the following diagram, where $\alpha = 20^\circ$ .

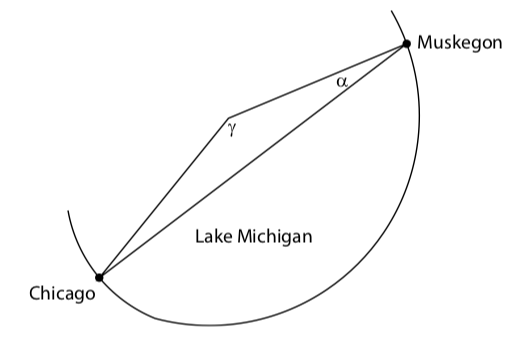
$e2.png$

Figure $\PageIndex{6}$

How far is the sailboat from Chicago at this time?
What is the degree measure of the angle $\gamma$ (to the nearest tenth) in the diagram? Through what angle should the boat turn to correct its course and be heading straight to Chicago?
Assuming the boat maintains a speed of $15$ miles per hour, how much time have they added to their trip by being off course?

Answer

The boat is about $67.8$ miles from Chicage.
$\gamma \approx 142.4^\circ$ . So the boat should turn through an angle of about $180^\circ - 142.4^\circ = 37.6^\circ$
The direct trip from Muskegon to Chicago would take $\dfrac{121}{15}$ hours or about $8.07$ hours. By going off-course, the trip now will take $\dfrac{127.8}{15}$ hours or about $8.52$ hours.

Exercise $\PageIndex{27}$

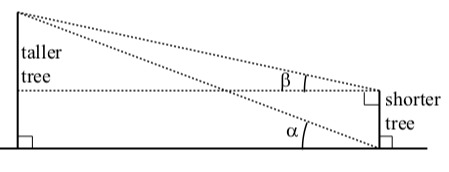
$e3.png$

Figure $\PageIndex{7}$

Two trees are on opposite sides of a river. It is known that the height taller of the shorter of the two trees is $13$ meters. A person makes the following angle measurements:

The angle of elevation from the base of the shorter tree to the top of the taller tree is $\alpha = 20^\circ$ .

The angle of elevation from the top of the shorter tree to the top of the taller tree is $\beta = 12^\circ$ .

Determine the distance between the bases of the two trees and the height of the taller tree.

Exercise $\PageIndex{28}$

One of the original Seven Wonders of the World, the Great Pyramid of Giza (also known as the Pyramid of Khufu or the Pyramid of Cheops), was believed to have been built in a $10$ to $20$ year period concluding around $2560$ B.C.E. It is also believed that the original height of the pyramid was $146.5$ meters but that it is now shorter due to erosion and the loss of some topmost stones.

To determine its current height, the angle of elevation from a distance of $30$ meters from the base of the pyramid was measured to be $46.12^\circ$ , and then the angle of elevation was measured to be $40.33^\circ$ from a distance of $60$ meters from the base of the pyramid as shown in the following diagram. Use this information to determine the height $h$ of the pyramid. ( $138.8$ meters)

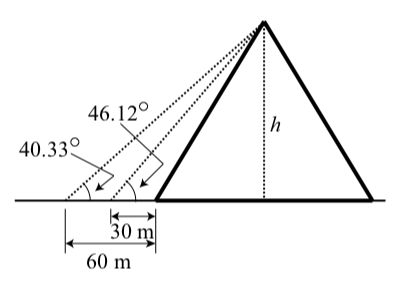
$e4.png$

Figure $\PageIndex{8}$

Exercise $\PageIndex{29}$

Two sides of a triangle have length $2.5$ meters and $3.5$ meters, and the angle formed by these two sides has a measure of $60^\circ$ . Determine the area of the triangle. Note: This is the triangle in Progress Check 3.17 on page 200.

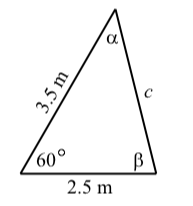
$e5.png$

Figure $\PageIndex{9}$

Exercise $\PageIndex{30}$

A field has the shape of a quadrilateral that is not a parallelogram. As shown in the following diagram, three sides measure $50$ yards, $60$ yards, and $70$ yards. Due to some wetland along the fourth side, the length of the fourth side could not be measured directly. The two angles shown in the diagram measure $127^\circ$ and $132^\circ$ .

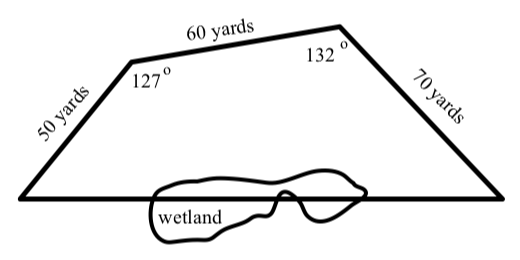
$e6.png$

Figure $\PageIndex{10}$

Determine the length of the fourth side of the quadrilateral, the measures of the other two angles in the quadrilateral, and the area of the quadrilateral. Lengths must be accurate to the nearest hundredth of a yard, angle measures must be correct to the nearest hundredth of a degree, and the area must be correct to the nearest hundredth of a square yard.

Exercise $\PageIndex{31}$

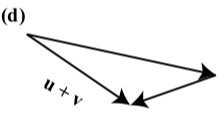
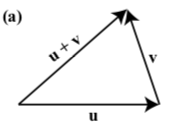
In each of the following diagrams, one of the vectors $\textbf{u}$ , $\textbf{v}$ , and $\textbf{u} + \textbf{v}$ is labeled. Label the vectors the other two vectors to make the diagram a valid representation of $\textbf{u} + \textbf{v}$

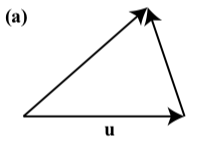
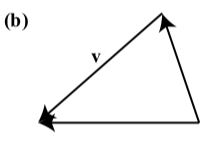
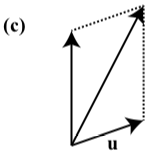
$e1a.png$ $e1b.png$ $e1c.png$ $e1d.png$

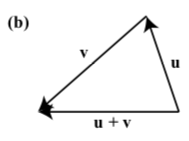
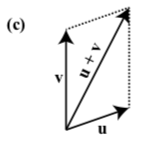
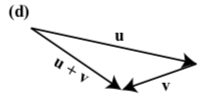
Answer: $3.5.1.png$ $3.5.2.png$ $3.5.3.png$ $3.5.4.png$

Exercise $\PageIndex{32}$

On the following diagram, draw the vectors $\textbf{u} + \textbf{v}$ , $\textbf{u} - \textbf{v}$ , $2\textbf{u} + \textbf{v}$ , and $2\textbf{u} - \textbf{v}$ .

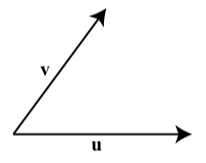
$e2.png$

Figure $\PageIndex{11}$

Answer

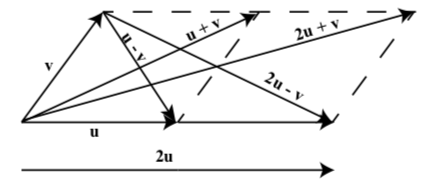
$3.5 2.png$

Figure $\PageIndex{12}$

Exercise $\PageIndex{33}$

In the following diagram, $|\textbf{a}| = 10$ and $|\textbf{a}| + |\textbf{b}| = 14$ . In addition, the angle $\theta$ between the vectors $\textbf{a}$ and $\textbf{b}$ is $30^\circ$ . Determine the magnitude of the vector $\textbf{b}$ and the angle between the vectors $\textbf{a}$ and $\textbf{a} + \textbf{b}$ .

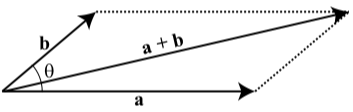
$e3.png$

Figure $\PageIndex{13}$

Answer: The angle between the vectors $\textbf{a}$ and $\textbf{a} + \textbf{b}$ is approximately $9.075^\circ$ . In addition, $|\textbf{b}| \approx 4.416$ .

Exercise $\PageIndex{34}$

Suppose that vectors $\textbf{a}$ and $\textbf{b}$ have magnitudes of 125 and 180, respectively. Also assume that the angle between these two vectors is $35^\circ$ . Determine the magnitude of the vector $\textbf{a} + \textbf{b}$ and the measure of the angle between the vectors $\textbf{a}$ and $\textbf{a} + \textbf{b}$ .

Exercise $\PageIndex{35}$

A car that weighs $3250$ pounds is on an inclined plane that makes an angle of $4.5^\circ$ with the horizontal. Determine the magnitude of the force of the car on the inclined plane, and determine the magnitude of the force on the car down the plane due to gravity. What is the magnitude of the smallest force necessary to keep the car from rolling down the plane?

Exercise $\PageIndex{36}$

An experiment determined that a force of $45$ pounds is necessary to keep a $250$ pound object from sliding down an inclined plane. Determine the angle the inclined plane makes with the horizontal.

Exercise $\PageIndex{37}$

A cable that can withstand a force of $4500$ pounds is used to pull an object up an inclined plane that makes an angle of 15 degrees with the horizontal. What is the heaviest object that can be pulled up this plane with the cable? (Assume that friction can be ignored.)

Exercise $\PageIndex{38}$

Determine the magnitude and the direction angle of each of the following vectors.

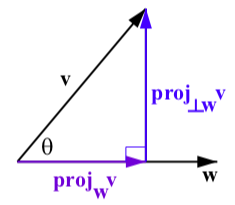
$3.33.png$

Figure $\PageIndex{14}$ : The Projection of $\textbf{v}$ onto $\textbf{w}$

$\textbf{v} = 3\textbf{i} + 5\textbf{j}$
$\textbf{w} = \langle -3, 6 \rangle$
$\textbf{a} = 4\textbf{i} - 7\textbf{j}$
$\textbf{u} = \langle -3, -5 \rangle$

Answer

$|\textbf{v}| = \sqrt{34}$ . The direction angle is approximately $59.036^\circ$ .
$|\textbf{w}| = \sqrt{45}$ . The direction angle is approximately $116.565^\circ$ .

Exercise $\PageIndex{39}$

Determine the horizontal and vertical components of each of the following vectors. Write each vector in $\textbf{i}$ , $\textbf{j}$ form.

The vector $\textbf{v}$ with magnitude 12 and direction angle $50^\circ$ ?

The vector $\textbf{u}$ with $\textbf{u} = \sqrt{20}$ and direction angle $125^\circ$ .

The vector $\textbf{w}$ with magnitude $5.25$ and direction angle $200^\circ$ .

Answer

$\textbf{v} = 12\cos(50^\circ) + 12\sin(50^\circ) \approx 7.713\textbf{i} + 9.193\textbf{j}$ .
$\textbf{u} = \sqrt{20}\cos(125^\circ) + \sqrt{20}\sin(125^\circ) \approx -2.565\textbf{i} + 3.663\textbf{j}$

Exercise $\PageIndex{40}$

Let $\textbf{u} = 2\textbf{i} + 3\textbf{j}$ , $\textbf{v} = -\textbf{i} + 5\textbf{j}$ , and $\textbf{w} = 4\textbf{i} - 2\textbf{j}$ . Determine the $\textbf{i}$ , $\textbf{j}$ form of each of the following:

$5\textbf{u} - \textbf{v}$
$2\textbf{v} + 7\textbf{w}$
$\textbf{u} + \textbf{v} + \textbf{w}$
$3\textbf{u} + 5\textbf{w}$

Answer

1. $5\textbf{u} - \textbf{v} = 11\textbf{i} + 10\textbf{j}$

3. $\textbf{u} + \textbf{v} + \textbf{w} = 5\textbf{i} + 6\textbf{j}$

Exercise $\PageIndex{41}$

Determine the value of the dot product for each of the following pairs of vectors.

$\textbf{v} = 2\textbf{i} + 5\textbf{j}$ and $\textbf{w} = 3\textbf{i} - 2\textbf{j}$
$\textbf{a}$ and $\textbf{b}$ where $|\textbf{a}| = 6$ , $|\textbf{w}| = 3$ , and the angle between $\textbf{v}$ and $\textbf{w}$ is $30^\circ$
$\textbf{a}$ and $\textbf{b}$ where $|\textbf{a}| = 6$ , $|\textbf{w}| = 3$ , and the angle between $\textbf{v}$ and $\textbf{w}$ is $150^\circ$
$\textbf{a}$ and $\textbf{b}$ where $|\textbf{a}| = 6$ , $|\textbf{w}| = 3$ , and the angle between $\textbf{v}$ and $\textbf{w}$ is $50^\circ$
$\textbf{a} = 5\textbf{i} - 2\textbf{j}$ and $\textbf{b} = 2\textbf{i} + 5\textbf{j}$

Answer

1. $\textbf{v}\cdot\textbf{w} = -4$ .

2. $\textbf{a}\cdot\textbf{b} = 9\sqrt{3}$ .

Exercise $\PageIndex{42}$

Determine the angle between each of the following pairs of vectors. $page260image47455552$

$\textbf{v} = 2\textbf{i} + 5\textbf{j}$ and $\textbf{w} = 3\textbf{i} - 2\textbf{j}$
$\textbf{a} = 5\textbf{i} - 2\textbf{j}$ and $\textbf{b} = 2\textbf{i} + 5\textbf{j}$
$\textbf{v} = 3\textbf{i} - 2\textbf{j}$ and $\textbf{w} = -\textbf{i} + 4\textbf{j}$

Answer: 1. The angle between $\textbf{v}$ and $\textbf{w}$ is $\cos^{-1}(\dfrac{-4}{\sqrt{29}\sqrt{13}}) \approx 101.89^\circ$ .

Exercise $\PageIndex{43}$

For each pair of vectors, determine $\textbf{proj}_{\textbf{v}}\textbf{w}$ , $\textbf{proj}_{\perp\textbf{v}}\textbf{w}$ and verify that

$\textbf{w} = \textbf{proj}_{\perp\textbf{w}}\textbf{v} + \textbf{proj}_{\textbf{w}}\textbf{v}$ . Draw a picture showing all of the vectors involved in this.

$\textbf{v} = 2\textbf{i} + 5\textbf{j}$ and $\textbf{w} = 3\textbf{i} - 2\textbf{j}$
$\textbf{v} = \langle -2, 3 \rangle$ and $\textbf{w} = \langle 1, 1 \rangle$

Answer

1. $\textbf{proj}_{v}\textbf{w} = \dfrac{\textbf{w}\cdot \textbf{v}}{\textbf{v}\cdot \textbf{v}}\textbf{v} = \dfrac{-4}{29}(2\textbf{i} + 5\textbf{j}) = -\dfrac{8}{29}\textbf{i} - \dfrac{20}{29}\textbf{j}$

$\textbf{proj}_{\perp_\textbf{v}}\textbf{w} = \textbf{w} - \textbf{proj}_{v}\textbf{w} = \dfrac{95}{29}\textbf{i} - \dfrac{38}{29}\textbf{j}$

Search

Text Color

Text Size

Margin Size

Font Type

Support Center

How can we help?