6.3: Complex Numbers

There is no real number \(x \) such that \(x^2 = -1 \). However, it turns out to be useful to invent such a number, called the imaginary unit and denoted by the letter \(i \). Thus, \(i^2 = -1 \), and hence \(i = \sqrt{-1} \). If \(a \) and \(b \) are real numbers, then a number of the form \(a + bi \) is called a complex number, and if \(b \ne 0 \) then it is called an imaginary number (and pure imaginary if \(a=0 \) and \(b \ne 0\)). The real number \(a \) is called the real part of the complex number \(a+bi \), and \(bi \) is called its imaginary part.

What does it mean to add \(a \) to \(bi \) in the definition \(a+bi \) of a complex number, i.e. adding a real number and an imaginary number? You can think of it as a way of extending the set of real numbers. If \(b=0 \) then \(a+bi = a+0i = a \) (since \(0i \) is defined as \(0\)), so that every real number is a complex number. The imaginary part \(bi \) in \(a+bi \) can be thought of as a way of taking the one-dimensional set of all real numbers and extending it to a two-dimensional set: there is a natural correspondence between a complex number \(a+bi \) and a point \((a,b) \) in the (two-dimensional) \(xy\)-coordinate plane.

Before exploring that correspondence further, we will first state some fundamental properties of and operations on complex numbers:

fundamental properties of and operations on complex numbers

Let \(a+bi \) and \(c+di \) be complex numbers. Then:

1. \(a+bi ~=~ c+di \) if and only if \(a=c \) and \(b=d~ \) (i.e. the real parts are equal and the imaginary parts are equal)
2. \((a+bi) \;+\; (c+di) ~=~ (a+c) \;+\; (b+d)i~ \) (i.e. add the real parts together and add the imaginary parts together)
3. \((a+bi) \;-\; (c+di) ~=~ (a-c) \;+\; (b-d)i\)
4. \((a+bi)\,(c+di) ~=~ (ac-bd) \;+\; (ad+bc)i\)
5. \((a+bi)\,(a-bi) ~=~ a^2 \;+\; b^2\)
6. \(\dfrac{a+bi}{c+di} ~=~ \dfrac{(ac+bd) \;+\; (bc-ad)i}{c^2 + d^2}\)

The first three items above are just definitions of equality, addition, and subtraction of complex numbers. The last three items can be derived by treating the multiplication and division of complex numbers as you would normally treat factors of real numbers:

\[\nonumber \begin{align*}
(a+bi)\,(c+di) ~&=~ a\,(c+di) \;+\; bi\,(c+di)\\ \nonumber
&=~ ac \;+\; adi \;+\; bci \;+\; bdi^2 ~=~ ac \;+\; adi \;+\; bci \;+\; bd(-1)\\ \nonumber
&=~ (ac - bd) \;+\; (ad+bc)i
\end{align*} \nonumber \]

The fifth item is a special case of the multiplication formula:

\[\nonumber \begin{align*}
(a+bi)\,(a-bi) ~&=~ ((a)(a) - (b)(-b)) \;+\; ((a)(-b) + (b)(a))i\\ \nonumber
&=~ ( a^2 + b^2 ) \;+\; (-ab + ba)i ~=~ ( a^2 + b^2 ) \;+\; 0i\\ \nonumber
&=~ a^2 \;+\; b^2
\end{align*} \nonumber \]

The sixth item comes from using the previous items:

\[ \nonumber \begin{align*}
\dfrac{a+bi}{c+di} ~&=~ \dfrac{a+bi}{c+di} \,\cdot\, \dfrac{c-di}{c-di}\\ \nonumber
&=~ \dfrac{(ac - b(-d)) \;+\; (a(-d) + bc)i}{c^2 + d^2}\\ \nonumber
&=~ \dfrac{(ac+bd) \;+\; (bc-ad)i}{c^2 + d^2}
\end{align*} \nonumber \]

The conjugate \(\overline{a+bi} \) of a complex number \(a+bi \) is defined as \(\overline{a+bi} = a-bi \). Notice that \((a+bi) \;+\; \overline{(a+bi)} ~=~ 2a \) is a real number, \((a+bi) \;-\; \overline{(a+bi)} ~=~ 2bi \) is an imaginary number if \(b \ne 0 \), and \((a+bi) \overline{(a+bi)} ~=~ a^2 + b^2 \) is a real number. So for a complex number \(z=a+bi \), \(z\,\overline{z} = a^2 + b^2 \, \) and thus we can define the modulus of \(z\) to be \(\sqrt{z\,\overline{z}} = \sqrt{a^2 + b^2} \), which we denote by \(|z| \).

Example 6.9

Let \(z_1 = -2+3i \) and \(z_2 = 3+4i \). Find \(z_1 + z_2 \), \(z_1 - z_2 \), \(z_1 \, z_2 \), \(z_1 / z_2 \), \(|z_1| \), and \(|z_2| \).

Solution

Using our rules and definitions, we have:

\[\nonumber \begin{align*}
z_1 \;+\; z_2 ~&=~ (-2+3i) \;+\; (3+4i)\\ \nonumber
&=~ 1 + 7i\\ \nonumber
z_1 \;-\; z_2 ~&=~ (-2+3i) \;-\; (3+4i)\\ \nonumber
&=~ -5 - i\\ \nonumber
z_1 \, z_2 ~&=~ (-2+3i)\, (3+4i)\\ \nonumber
&=~ ((-2)(3) - (3)(4)) \;+\; ((-2)(4) + (3)(3))i\\ \nonumber
&=~ -18 + i\\ \nonumber
\dfrac{z_1}{z_2} ~&=~ \dfrac{-2+3i}{3+4i}\\ \nonumber
&=~ \dfrac{(-2)(3) + (3)(4) \;+\; ((3)(3) - (-2)(4))i}{3^2 + 4^2}\\ \nonumber
&=~ \dfrac{6}{25} \;+\; \dfrac{17}{25}\,i\\ \nonumber
|z_1| ~&=~ \sqrt{(-2)^2 + 3^2}\\ \nonumber
&=~ \sqrt{13}\\ \nonumber
|z_2| ~&=~ \sqrt{3^2 + 4^2}\\ \nonumber
&=~ 5
\end{align*} \nonumber \]

We know that any point \((x,y) \) in the \(xy\)-coordinate plane that is a distance \(r >0 \) from the origin has coordinates \(x=r\,\cos\;\theta \) and \(y=r\,\sin\;\theta \), where \(\theta \) is the angle in standard position as in Figure 6.3.1(a).

Figure 6.3.1

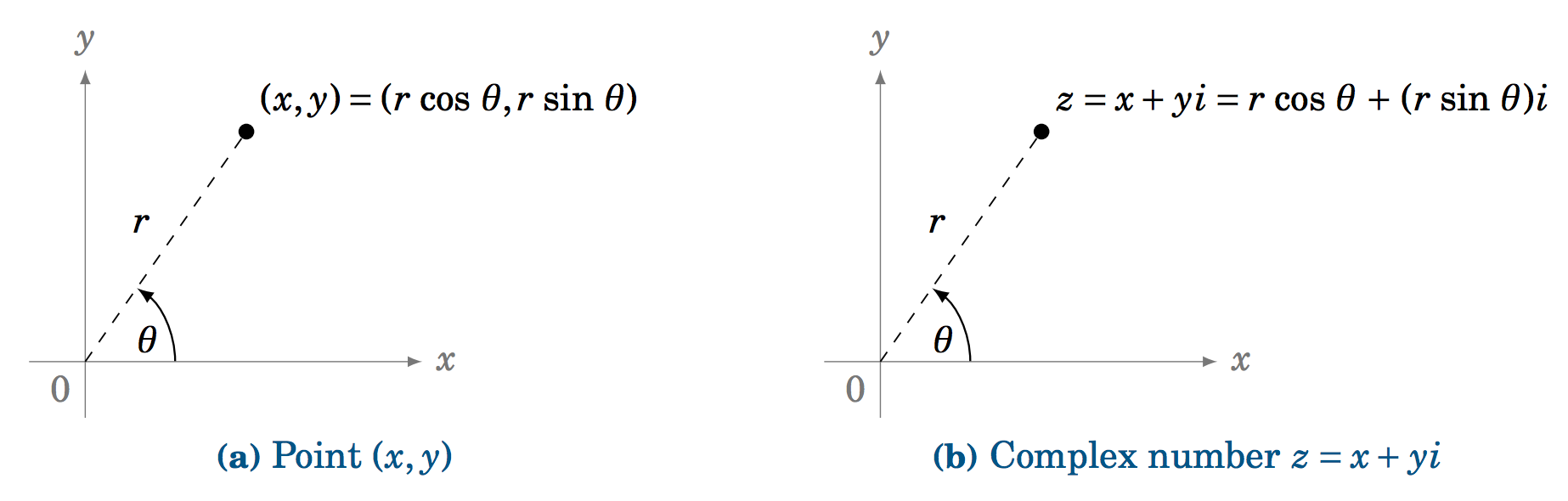
Let \(z=x+yi \) be a complex number. We can represent \(z \) as a point in the complex plane, where the horizontal \(x\)-axis represents the real part of \(z \), and the vertical \(y\)-axis represents the pure imaginary part of \(z \), as in Figure 6.3.1(b). The distance \(r \) from \(z \) to the origin is, by the Pythagorean Theorem, \(r = \sqrt{x^2 + y^2} \), which is just the modulus of \(z \). And we see from Figure 6.3.1(b) that \(x=r\,\cos\;\theta \) and \(y=r\,\sin\;\theta \), where \(\theta \) is the angle formed by the positive \(x\)-axis and the line segment from the origin to \(z \). We call this angle \(\theta \) the argument of \(z \). Thus, we get the trigonometric form (sometimes called the polar form) of the complex number \(z\):

For any complex number \(z=x+yi \), we can write

\[\begin{align}
z ~&=~ r\,(\cos\;\theta \;+\; i\,\sin\;\theta)~~,~\text{where}\label{eqn:polar}\\
r ~&=~ |z| ~=~ \sqrt{x^2 + y^2}~~\text{and}\nonumber\\
\theta ~&=~ \text{the argument of \(z\)}~.\nonumber \end{align} \nonumber \]

The representation \(z=r\,(\cos\;\theta \;+\; i\,\sin\;\theta) \) is often abbreviated as:

\[ z ~=~ r\,\text{cis}\;\theta\label{eqn:cis} \]

In the special case \(z=0 = 0+0i \), the argument \(\theta \) is undefined since \(r=|z|=0 \). Also, note that the argument \(\theta \) can be replaced by \(\theta \;+\; 360^\circ k \) or \(\theta \;+\; \pi k \), depending on whether you are using degrees or radians, respectively, for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(... \). Note also that for \(z=x+yi \) with \(r=|z| \), \(\theta \) must satisfy

\[\nonumber \tan\;\theta ~=~ \tfrac{y}{x}~~,~ \cos\;\theta ~=~ \tfrac{x}{r}~~,~ \sin\;\theta ~=~ \tfrac{y}{r}~. \nonumber \]

Example 6.10

Represent the complex number \(-2 - i \) in trigonometric form.

Figure 6.3.2

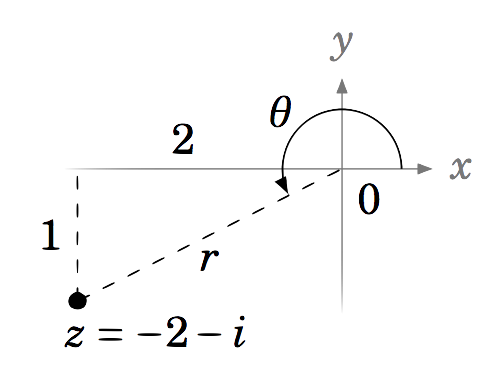
Solution:

Let \(z=-2-i=x+yi \), so that \(x=-2 \) and \(y=-1 \). Then \(\theta \) is in QIII, as we see in Figure 6.3.2. So since \(\tan\;\theta = \tfrac{y}{x} = \tfrac{-1}{-2} = \tfrac{1}{2} \), we have \(\theta = 206.6^\circ \). Also,

\[\nonumber r ~=~ \sqrt{x^2 + y^2} ~=~ \sqrt{(-2)^2 + (-1)^2} ~=~ \sqrt{5} ~. \nonumber \]

Thus, \(\boxed{-2 - i = \sqrt{5}\;(\cos\;206.6^\circ \;+\; i\,\sin\;206.6^\circ)}\; \), or \(\sqrt{5}\;\text{cis}\;206.6^\circ \).

For complex numbers in trigonometric form, we have the following Equations for multiplication and division:

Let \(z_1 = r_1 \,(\cos\;\theta_1 \;+\; i\,\sin\;\theta_1 ) \) and \(z_2 = r_2 \,(\cos\;\theta_2 \;+\; i\,\sin\;\theta_2 ) \) be complex numbers. Then

\[\begin{align}
z_1 \, z_2 ~&=~ r_1 \, r_2 \,(\cos\;(\theta_1 + \theta_2 ) \;+\; i\,\sin\;(\theta_1 +
\theta_2 ))~\text{, and}\label{eqn:complextrigmult}\\
\frac{z_1}{z_2} ~&=~ \frac{r_1}{r_2} \,(\cos\;(\theta_1 - \theta_2 ) \;+\; i\,\sin\;(\theta_1 -
\theta_2 ))\quad\text{if \(z_2 \ne 0 \).}\label{eqn:complextrigdiv}\end{align} \]

The proofs of these Equations are straightforward:

\[\nonumber \begin{align*}
z_1 \, z_2 ~&=~ r_1 \,(\cos\;\theta_1 \;+\; i\,\sin\;\theta_1 ) \;\cdot\;
r_2 \,(\cos\;\theta_2 \;+\; i\,\sin\;\theta_2 )\\ \nonumber
&=~ r_1 \, r_2 \,\left[ (\cos\;\theta_1 ~ \cos\;\theta_2 \;-\; \sin\;\theta_1 ~ \sin\;\theta_2 )
\;+\; i\,(\sin\;\theta_1 ~ \cos\;\theta_2 \;+\; \cos\;\theta_1 ~ \sin\;\theta_2 ) \right]\\ \nonumber
&=~ r_1 \, r_2 \,(\cos\;(\theta_1 + \theta_2 ) \;+\; i\,\sin\;(\theta_1 + \theta_2 )) \end{align*} \nonumber \]

by the addition Equations for sine and cosine. And

\[\nonumber \begin{align*} \frac{z_1}{z_2} ~&=~ \frac{r_1 \,(\cos\;\theta_1 \;+\; i\,\sin\;\theta_1 )}{
r_2 \,(\cos\;\theta_2 \;+\; i\,\sin\;\theta_2 )}\\ \nonumber
&=~ \frac{r_1}{r_2} \;\cdot\; \frac{\cos\;\theta_1 \;+\; i\,\sin\;\theta_1}{
\cos\;\theta_2 \;+\; i\,\sin\;\theta_2} \;\cdot\; \frac{\cos\;\theta_2 \;-\; i\,\sin\;\theta_2}{
\cos\;\theta_2 \;-\; i\,\sin\;\theta_2}\\ \nonumber
&=~ \frac{r_1}{r_2} \;\cdot\; \frac{(\cos\;\theta_1 ~ \cos\;\theta_2 \;+\; \sin\;\theta_1 ~
\sin\;\theta_2 ) \;+\; i\,(\sin\;\theta_1 ~ \cos\;\theta_2 \;-\; \cos\;\theta_1 ~
\sin\;\theta_2 )}{\cos^2 \,\theta_2 \;+\; \sin^2 \,\theta_2}\\ \nonumber
&=~ \frac{r_1}{r_2} \,(\cos\;(\theta_1 - \theta_2 ) \;+\; i\,\sin\;(\theta_1 - \theta_2 ))
\end{align*} \nonumber \]

by the subtraction Equations for sine and cosine, and since \(\cos^2 \,\theta_2 \;+\; \sin^2 \,\theta_2 = 1 \). QED

Note that Equations \ref{eqn:complextrigmult} and \ref{eqn:complextrigdiv} say that when multiplying complex numbers the moduli are multiplied and the arguments are added, while when dividing complex numbers the moduli are divided and the arguments are subtracted. This makes working with complex numbers in trigonometric form fairly simple.

Example 6.11

Let \(z_1 = 6\,(\cos\;70^\circ \;+\; i\,\sin\;70^\circ ) \) and \(z_1 = 2\,(\cos\;31^\circ \;+\; i\,\sin\;31^\circ ) \). Find \(z_1 \, z_2 \) and \(\frac{z_1}{z_2} \).

Solution

By Equations \ref{eqn:complextrigmult} and \ref{eqn:complextrigdiv} we have

\[\nonumber \begin{alignat*}{3}
z_1 \, z_2 ~&=~ (6) \, (2) \, (\cos\;(70^\circ + 31^\circ ) \;+\; i\,\sin\;(70^\circ +
31^\circ )) \quad&&\Rightarrow\quad \boxed{z_1 \, z_2 ~=~ 12 \, (\cos\;101^\circ \;+\;
i\,\sin\;101^\circ )} ~\text{, and}\\ \nonumber
\frac{z_1}{z_2} ~&=~ \frac{6}{2} \, (\cos\;(70^\circ - 31^\circ ) \;+\; i\,\sin\;(70^\circ -
31^\circ )) \quad&&\Rightarrow\quad \boxed{\frac{z_1}{z_2} ~=~ 3 \, (\cos\;39^\circ \;+\;
i\,\sin\;39^\circ )} ~.
\end{alignat*} \nonumber \]

For the special case when \(z_1 = z_2 = z = r\,(\cos\;\theta \;+\; i\,\sin\;\theta) \) in Equation \ref{eqn:complextrigmult}, we have

\[\nonumber \begin{align*}
\left[ r\,(\cos\;\theta \;+\; i\,\sin\;\theta)\right]^2 ~&=~
r \cdot r \,(\cos\;(\theta + \theta ) \;+\; i\,\sin\;(\theta + \theta))\\ \nonumber
&=~ r^2 \,(\cos\;2\theta \;+\; i\,\sin\;2\theta) ~,\end{align*} \nonumber \]

and so

\[\nonumber \begin{align*} \left[ r\,(\cos\;\theta \;+\; i\,\sin\;\theta)\right]^3 ~&=~
\left[ r\,(\cos\;\theta \;+\; i\,\sin\;\theta)\right]^2 \;\cdot\;
r\,(\cos\;\theta \;+\; i\,\sin\;\theta )\\ \nonumber
&=~ r^2 \,(\cos\;2\theta \;+\; i\,\sin\;2\theta) \;\cdot\;
r\,(\cos\;\theta \;+\; i\,\sin\;\theta )\\ \nonumber
&=~ r^3 \,(\cos\;(2\theta + \theta) \;+\; i\,\sin\;(2\theta + \theta) )\\ \nonumber
&=~ r^3 \,(\cos\;3\theta \;+\; i\,\sin\;3\theta) ~,
\end{align*} \nonumber \]

and continuing like this (i.e. by mathematical induction), we get:

Theorem 6.1 De Moivre's Theorem

For any integer \(n \ge 1 \),

\[\label{eqn:demoivre}
\left[ r\,(\cos\;\theta \;+\; i\,\sin\;\theta )\right]^n ~=~
r^n \,(\cos\;n\theta \;+\; i\,\sin\;n\theta ) ~. \nonumber \]

We define \(z^0 = 1 \) and \(z^{-n} = 1/z^n \) for all integers \(n \ge 1 \). So by De Moivre's Theorem and Equation \ref{eqn:complextrigmult}, for any \(z=r\,(\cos\;\theta \;+\; i\,\sin\;\theta) \) and integer \(n \ge 1 \) we get

\[\nonumber \begin{align*}
z^{-n} ~&=~ \frac{1}{z^n}\\ \nonumber
&=~ \frac{1\,(\cos\;0^\circ \;+\; i\,\sin\;0^\circ )}{r^n \,(\cos\;n\theta \;+\;
i\,\sin\;n\theta )}\\ \nonumber
&=~ \frac{1}{r^n} \,(\cos\;(0^\circ - n\theta) \;+\; i\,\sin\;(0^\circ - n\theta))\\ \nonumber
&=~ r^{-n} \, (\cos\;(- n\theta) \;+\; i\,\sin\;(- n\theta)) ~,
\end{align*} \nonumber \]

and so De Moivre's Theorem in fact holds for all integers.

Example 6.12

Find \((1+i)^{10} \).

Solution

Since \(1+i = \sqrt{2}\;(\cos\;45^\circ \;+\; i\,\sin\;45^\circ )\) (why?), by De Moivre's Theorem we have

\[\nonumber (1+i)^{10} ~=~ (\sqrt{2})^{10} \;(\cos\;450^\circ \;+\; i\,\sin\;450^\circ ) ~=~
2^{10/2} \;(0 \;+\; i\,(1)) ~=~ 2^5 \,\cdot\, i ~=~ \boxed{32i} ~. \nonumber \]

We can use De Moivre's Theorem to find the \(n^{th} \) roots of a complex number. That is, given any complex number \(z \) and positive integer \(n \), find all complex numbers \(w \) such that \(w^n = z \). Let \(z=r\,(\cos\;\theta \;+\; i\,\sin\;\theta) \). Since the cosine and sine functions repeat every \(360^\circ \), we know that \(z=r\,(\cos\;(\theta + 360^\circ k)\;+\; i\,\sin\;(\theta + 360^\circ k)) \) for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(... \). Now let \(w=r_0 \,(\cos\;\theta_0 \;+\; i\,\sin\;\theta_0 ) \) be an \(n^{th} \) root of \(z \). Then

\[\nonumber \begin{align*}
w^n ~=~ z \quad&\Rightarrow\quad \left[ r_0 \,(\cos\;\theta_0 \;+\; i\,\sin\;\theta_0 )\right]^n
~=~ r\,(\cos\;(\theta + 360^\circ k)\;+\; i\,\sin\;(\theta + 360^\circ k))\\ \nonumber
&\Rightarrow\quad r_0^n \,(\cos\;n\theta_0 \;+\; i\,\sin\;n\theta_0 )
~=~ r\,(\cos\;(\theta + 360^\circ k)\;+\; i\,\sin\;(\theta + 360^\circ k))\\ \nonumber
&\Rightarrow\quad r_0^n ~=~ r \quad\text{and}\quad n\theta_0 ~=~ \theta + 360^\circ k\\ \nonumber
&\Rightarrow\quad r_0 ~=~ r^{1/n} \quad\text{and}\quad \theta_0 ~=~
\frac{\theta + 360^\circ k}{n} ~.
\end{align*} \nonumber \]

Since the cosine and sine of \(\frac{\theta + 360^\circ k}{n} \) will repeat for \(k \ge n \), we get the following Equation for the \(n^{th} \) roots of \(z\):

For any nonzero complex number \(z=r\,(\cos\;\theta \;+\; i\,\sin\;\theta) \) and positive integer \(n \), the \(n \) distinct \(n^{th}\) roots of \(z \) are

\[\label{eqn:nthroots}
r^{1/n} \, \left[ \cos\;\left(\frac{\theta + 360^\circ k}{n}\right) \;+\;
i\,\sin\;\left(\frac{\theta + 360^\circ k}{n}\right) \right] \nonumber \]

for \(k=0 \), \(1 \), \(2 \), \(... \), \(n-1 \).

Note: An \(n^{th} \) root of \(z \) is usually written as \(z^{1/n} \) or \(\sqrt[n]{z} \). The number \(r^{1/n} \) in the above Equation is the usual real \(n^{th} \) root of the real number \(r=|z| \).

Example 6.13

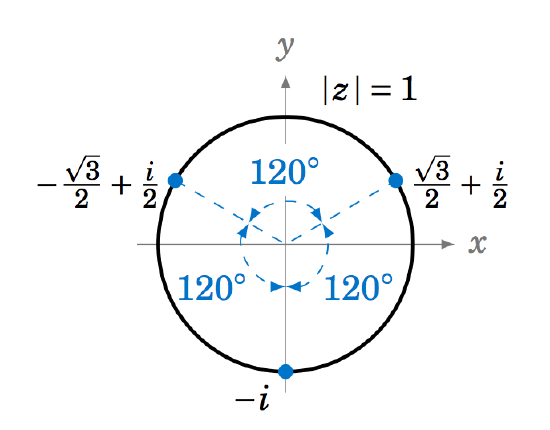
Find the three cube roots of \(i \).

Solution:

Since \(i = 1\,(\cos\;90^\circ \;+\; i\,\sin\;90^\circ) \), the three cube roots of \(i \) are:

\[\nonumber \begin{alignat*}{3}
\sqrt[3]{1} \;\left[ \cos\;\left(\frac{90^\circ + 360^\circ (0)}{3}\right) \;+\;
i\,\sin\;\left(\frac{90^\circ + 360^\circ (0)}{3}\right) \right] ~&=~
\cos\;30^\circ \;+\; i\,\sin\;30^\circ ~&&=~
\boxed{\frac{\sqrt{3}}{2} \;+\; \frac{1}{2}\,i}~,\\ \nonumber
\sqrt[3]{1} \;\left[ \cos\;\left(\frac{90^\circ + 360^\circ (1)}{3}\right) \;+\;
i\,\sin\;\left(\frac{90^\circ + 360^\circ (1)}{3}\right) \right] ~&=~
\cos\;150^\circ \;+\; i\,\sin\;150^\circ ~&&=~
\boxed{-\frac{\sqrt{3}}{2} \;+\; \frac{1}{2}\,i}~,\\ \nonumber
\sqrt[3]{1} \;\left[ \cos\;\left(\frac{90^\circ + 360^\circ (2)}{3}\right) \;+\;
i\,\sin\;\left(\frac{90^\circ + 360^\circ (2)}{3}\right) \right] ~&=~
\cos\;270^\circ \;+\; i\,\sin\;270^\circ ~&&=~ \boxed{-i}
\end{alignat*} \nonumber \]

Notice from Example 6.13 that the three cube roots of \(i \) are equally spaced points along the unit circle \(|z|=1 \) in the complex plane, as shown in Figure 6.3.3. We see that consecutive cube roots are \(120^\circ \) apart. In general, the \(n \) \(n^{th} \) roots of a complex number \(z \) will be equally spaced points along the circle of radius \(|z|^{1/n} \) in the complex plane, with consecutive roots separated by \(\tfrac{360^\circ}{n} \).

Figure 6.3.3

In higher mathematics the Fundamental Theorem of Algebra states that every polynomial of degree \(n \) with complex coefficients has \(n \) complex roots (some of which may repeat). In particular, every real number \(a \) has \(n \) \(n^{th} \) roots (being the roots of \(z^n - a\)). For example, the square roots of \(1 \) are \(\pm\,1 \), and the square roots of \(-1 \) are \(\pm\,i \).