7.1: A - Complex Numbers
- Page ID
- 70217
In this Appendix we give a brief review of the arithmetic and basic properties of the complex numbers.
As motivation, notice that the rotation matrix
\[ A =\left(\begin{array}{cc}0&-1\\1&0\end{array}\right) \nonumber \]
has characteristic polynomial \(f(\lambda) = \lambda^2 + 1\). A zero of this function is a square root of \(-1\). If we want this polynomial to have a root, then we have to use a larger number system: we need to declare by fiat that there exists a square root of \(-1\).
- The imaginary number \(i\) is defined to satisfy the equation \(i^2 = -1\).
- A complex number is a number of the form \(a+bi\text{,}\) where \(a,b\) are real numbers.
The set of all complex numbers is denoted \(\mathbb{C}\).
The real numbers are just the complex numbers of the form \(a + 0i\text{,}\) so that \(\mathbb{R}\) is contained in \(\mathbb{C}\).
We can identify \(\mathbb{C}\) with \(\mathbb{R}^2 \) by \(a+bi \longleftrightarrow {a\choose b}\). So when we draw a picture of \(\mathbb{C}\text{,}\) we draw the plane:
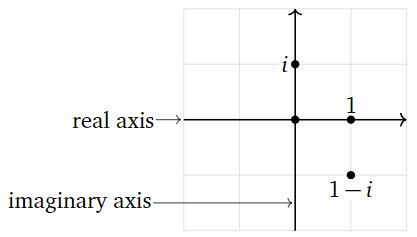
Figure \(\PageIndex{1}\)
We can perform all of the usual arithmetic operations on complex numbers: add, subtract, multiply, divide, absolute value. There is also an important new operation called complex conjugation.
- Addition is performed component-wise:
\[ (a + bi) + (c + di) = (a + c) + (b + d)i. \nonumber \]
- Multiplication is performed using distributivity and \(i^2=-1\text{:}\)
\[ (a+bi)(c+di) = ac + adi + bci + bdi^2 = (ac-bd) + (ad+bc)i. \nonumber \]
- Complex conjugation replaces \(i\) with \(-i\text{,}\) and is denoted with a bar:
\[ \overline{a+bi} = a - bi. \nonumber \] The number \(\overline{a+bi}\) is called the complex conjugate of \(a+bi\). One checks that for any two complex numbers \(z,w\text{,}\) we have
\[ \overline{z+w} = \overline{ z} + \overline{ w} \quad\text{and}\quad \overline{zw} = \overline{z}\cdot\overline{w}. \nonumber \] Also, \((a+bi)(a-bi) = a^2 + b^2\text{,}\) so \(z\bar z\) is a nonnegative real number for any complex number \(z\).
- The absolute value of a complex number \(z\) is the real number \(|z| = \sqrt{z\overline{ z}}\text{:}\)
\[ |a+bi| = \sqrt{a^2 + b^2}. \nonumber \] One checks that \(|zw| = |z|\cdot|w|.\)
- Division by a nonzero real number proceeds component-wise:
\[ \frac{a+bi}c = \frac ac + \frac bci. \nonumber \]
- Division by a nonzero complex number requires multiplying the numerator and denominator by the complex conjugate of the denominator:
\[ \frac zw = \frac{z\overline{ w}}{w\overline{ w}} = \frac{z\overline{ w}}{|w|^2}. \nonumber \] For example,
\[ \frac{1+i}{1-i} = \frac{(1+i)^2}{1^2+(-1)^2} = \frac{1+2i+i^2}2 = i. \nonumber \]
- The real and imaginary parts of a complex number are
\[ \Re(a+bi) = a \qquad \Im(a+bi) = b. \nonumber \]
The point of introducing complex numbers is to find roots of polynomials. It turns out that introducing \(i\) is sufficent to find the roots of any polynomial.
Every polynomial of degree \(n\) has exactly \(n\) (real and) complex roots, counted with multiplicity.
Equivalently, if \(f(x) = x^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0\) is a polynomial of degree \(n\text{,}\) then \(f\) factors as
\[ f(x) = (x-\lambda_1)(x-\lambda_2)\cdots(x-\lambda_n) \nonumber \]
for (not necessarily distinct) complex numbers \(\lambda_1,\lambda_2,\ldots,\lambda_n\).
The quadratic formula gives the roots of a degree-2 polynomial, real or complex:
\[ f(x) = x^2 + bx + c \implies x = \frac{-b \pm \sqrt{b^2 - 4c}}2. \nonumber \]
For example, if \(f(x) = x^2 - \sqrt 2x + 1\text{,}\) then
\[ x = \frac{\sqrt 2\pm\sqrt{-2}}2 = \frac{\sqrt 2}2(1\pm i) = \frac{1\pm i}{\sqrt 2}. \nonumber \]
Note that if \(b,c\) are real numbers, then the two roots are complex conjugates.
A complex number \(z\) is real if and only if \(z = \bar z\). This leads to the following observation.
If \(f\) is a polynomial with real coefficients, and if \(\lambda\) is a complex root of \(f\text{,}\) then so is \(\overline{\lambda}\text{:}\)
\[\begin{aligned}0=\overline{f(\lambda )}&=\overline{\lambda^n+a_{n-1}\lambda^{n-1}+\cdots +a_1\lambda +a_0} \\ &=\overline{\lambda}^n+a_{n-1}\overline{\lambda}^{n-1}+\cdots +a_1\overline{\lambda}+a_0=f(\overline{\lambda}).\end{aligned}\]
Therefore, complex roots of real polynomials come in conjugate pairs.
A real cubic polynomial has either three real roots, or one real root and a conjugate pair of complex roots.
For example, \(f(x) = x^3-x = x(x-1)(x+1)\) has three real roots; its graph looks like this:
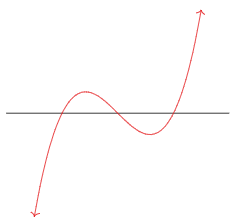
Figure \(\PageIndex{2}\)
On the other hand, the polynomial
\[ g(x) = x^3-5x^2+x-5 = (x-5)(x^2+1) = (x-5)(x+i)(x-i) \nonumber \]
has one real root at \(5\) and a conjugate pair of complex roots \(\pm i\). Its graph looks like this:
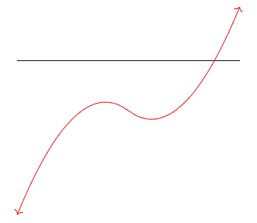
Figure \(\PageIndex{3}\)