15.4: Complex Numbers
- Page ID
- 34271
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The numbers you are most familiar with are called real numbers. These include numbers like 4, 275, -200, 10.7, ½, π, and so forth. All these real numbers can be plotted on a number line. For example, if we wanted to show the number 3, we plot a point:
To solve certain problems like \(x^{2}=-4\), it became necessary to introduce imaginary numbers.
The imaginary number \(i\) is defined to be \(i=\sqrt{-1}\).
Any real multiple of \(i\), like \(5i\), is also an imaginary number.
Simplify \(\sqrt{-9}\).
Solution
We can separate \(\sqrt{-9}\) as \(\sqrt{9} \sqrt{-1} .\) We can take the square root of \(9,\) and write the square root of -1 as \(i\)
\[\sqrt{-9}=\sqrt{9} \sqrt{-1}=3 i \nonumber \]
A complex number is a number \(z=a+b i,\) where \(a\) and \(b\) are real numbers
- \(a\) is the real part of the complex number
- \(b\) is the imaginary part of the complex number
To plot a complex number like \(3-4 i\), we need more than just a number line since there are two components to the number. To plot this number, we need two number lines, crossed to form a complex plane.
In the complex plane, the horizontal axis is the real axis and the vertical axis is the imaginary axis.
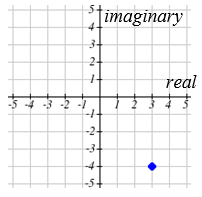
Plot the number \(3-4 i\) on the complex plane.
Solution
The real part of this number is 3, and the imaginary part is -4. To plot this, we draw a point 3 units to the right of the origin in the horizontal direction and 4 units down in the vertical direction.
Because this is analogous to the Cartesian coordinate system for plotting points, we can think about plotting our complex number \(z=a+b i\) as if we were plotting the point \((a, b)\) in Cartesian coordinates. Sometimes people write complex numbers as \(z=x+y i\) to highlight this relation.
Arithmetic on Complex Numbers
Before we dive into the more complicated uses of complex numbers, let’s make sure we remember the basic arithmetic involved. To add or subtract complex numbers, we simply add the like terms, combining the real parts and combining the imaginary parts.
Add \(3-4 i\) and \(2+5 i\).
Solution
Adding \((3-4 i)+(2+5 i),\) we add the real parts and the imaginary parts
\(3+2-4 i+5 i\)
\(5+i\)
Subtract \(2+5 i\) from \(3-4 i\).
- Answer
-
\((3-4 i)-(2+5 i)=1-9 i\)
When we add complex numbers, we can visualize the addition as a shift, or translation, of a point in the complex plane.
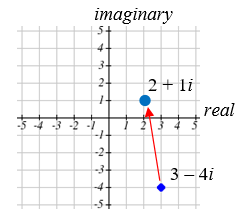
Visualize the addition \(3-4 i\) and \(-1+5 i\).
Solution
The initial point is \(3-4 i\). When we add \(-1+3 i\), we add -1 to the real part, moving the point 1 units to the left, and we add 5 to the imaginary part, moving the point 5 units vertically. This shifts the point \(3-4 i\) to \(2+1 i\).
We can also multiply complex numbers by a real number, or multiply two complex numbers.
Multiply: \(4(2+5 i)\)
Solution
To multiply the complex number by a real number, we simply distribute as we would when multiplying polynomials.
\(\begin{array}{ll} 4(2+5 i) & \text{Distribute} \\ =4 \cdot 2+4 \cdot 5 i & \text{Simplify} \\ =8+20 i \end{array}\)
Multiply: \((2+5 i)(4+i)\)
Solution
To multiply the complex number by a complex number, we simply distribute as we would when multiplying polynomials.
\(\begin{array}{ll} (2+5 i)(4+i) & \text{Expand} \\ =8+20 i+2 i+5 i^{2} & \text{Since }i=\sqrt{-1}, i^{2}=-1 \\ =8+20 i+2 i+5(-1) & \text{Simplify} \\ =3+22 i \end{array}\)
Multiply \(3-4 i\) and \(2+3 i\).
- Answer
-
Multiply \((3-4 i)(2+3 i)=6+9 i-8 i-12 i^{2}=6+i-12(-1)=18+i\)
To understand the effect of multiplication visually, we’ll explore three examples.
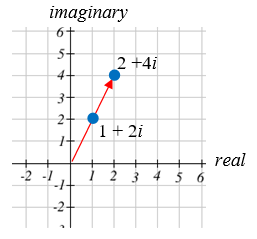Visualize the product \(2(1+2 i)\)
Solution
Multiplying we’d get
\(2 \cdot 1+2 \cdot 2 i = 2+4 i\)
Notice both the real and imaginary parts have been scaled by 2. Visually, this will stretch the point outwards, away from the origin.
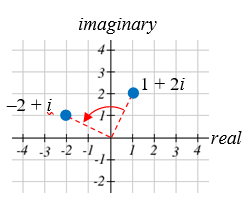Visualize the product \(i(1+2 i)\)
Solution
Multiplying, we’d get
\(i \cdot 1+i \cdot 2 i = i+2 i^{2}=i+2(-1)=-2+i\)
In this case, the distance from the origin has not changed, but the point has been rotated about the origin, 90° counter-clockwise.
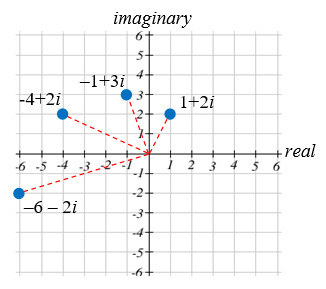Visualize the result of multiplying \(1+2 i\) by \(1+i .\) Then show the result of multiplying by \(1+i\) again.
Solution
Multiplying \(1+2 i\) by \(1+i\),
\((1+2 i)(1+i)=1+i+2 i+2 i^{2}=1+3 i+2(-1)=-1+3 i\)
Multiplying by \(1+i\) again,
\((-1+3 i)(1+i) =-1-i+3 i+3 i^{2} =-1+2 i+3(-1) =-4+2 i\)
If we multiplied by \(1+i\) again, we’d get \(–6–2i\). Plotting these numbers in the complex plane, you may notice that each point gets both further from the origin, and rotates counterclockwise, in this case by 45°.
In general, multiplication by a complex number can be thought of as a scaling, changing the distance from the origin, combined with a rotation about the origin.