15.5: Complex Recursive Sequences
- Page ID
- 34272
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We will now explore recursively defined sequences of complex numbers.
A recursive relationship is a formula which relates the next value, \(z_{n+1},\) in a sequence to the previous value, \(z_{n} .\) In addition to the formula, we need an initial value, \(z_{0}\).
The sequence of values produced is the recursive sequence.
Given the recursive relationship \(z_{n+1}=z_{n}+2, \quad z_{0}=4,\) generate several terms of the
recursive sequence.
Solution
We are given the starting value, \(z_{0}=4 .\) The recursive formula holds for any value of \(n,\) so
if \(n=0,\) then \(z_{n+1}=z_{n}+2\) would tell us \(z_{0+1}=z_{0}+2,\) or more simply, \(z_{1}=z_{0}+2\)
Notice this defines \(z_{1}\) in terms of the known \(z_{0},\) so we can compute the value:
\( z_{1}=z_{0}+2=4+2=6 \)
Now letting \(n=1,\) the formula tells us \(z_{1+1}=z_{1}+2,\) or \(z_{2}=z_{1}+2 .\) Again, the formula gives the next value in the sequence in terms of the previous value.
(z_{2}=z_{1}+2=6+2=8\)
Continuing,
\(z_{3}=z_{2}+2=8+2=10\)
\(z_{4}=z_{3}+2=10+2=12\)
The previous example generated a basic linear sequence of real numbers. The same process can be used with complex numbers.
Given the recursive relationship \(z_{n+1}=z_{n} \cdot i+(1-i), \quad z_{0}=4,\) generate several terms of the
recursive sequence.
Solution
We are given \(z_{0}=4 .\) Using the recursive formula:
\(z_{1}=z_{0} \cdot i+(1-i)=4 \cdot i+(1-i)=1+3 i\)
\(z_{2}=z_{1} \cdot i+(1-i)=(1+3 i) \cdot i+(1-i)=i+3 i^{2}+(1-i)=i-3+(1-i)=-2\)
\(z_{3}=z_{2} \cdot i+(1-i)=(-2) \cdot i+(1-i)=-2 i+(1-i)=1-3 i\)
\(z_{4}=z_{3} \cdot i+(1-i)=(1-3 i) \cdot i+(1-i)=i-3 i^{2}+(1-i)=i+3+(1-i)=4\)
\(z_{5}=z_{4} \cdot i+(1-i)=4 \cdot i+(1-i)=1+3 i\)
Notice this sequence is exhibiting an interesting pattern – it began to repeat itself.
Mandelbrot Set
The Mandelbrot Set is a set of numbers defined based on recursive sequences
For any complex number \(c,\) define the sequence \(z_{n+1}=z_{n}^{2}+c, \quad z_{0}=0\)
If this sequence always stays close to the origin (within 2 units), then the number \(c\) is part of the Mandelbrot Set. If the sequence gets far from the origin, then the number \(c\) is not part of the set.
Determine if \(c=1+i\) is part of the Mandelbrot set.
Solution
We start with \(z_{0}=0\). We continue, omitting some detail of the calculations
\(z_{1}=z_{0}^{2}+1+i=0+1+i=1+i\)
\(z_{2}=z_{1}^{2}+1+i=(1+i)^{2}+1+i=1+3 i\)
\(z_{3}=z_{2}^{2}+1+i=(1+3 i)^{2}+1+i=-7+7 i\)
\(z_{4}=z_{3}^{2}+1+i=(-7+7 i)^{2}+1+i=1-97 i\)
We can already see that these values are getting quite large. It does not appear that \(c=1+i\) is part of the Mandelbrot set.
Determine if \(c=0.5 i\) is part of the Mandelbrot set.
Solution
We start with \(z_{0}=0\). We continue, omitting some detail of the calculations
\(z_{1}=z_{0}^{2}+0.5 i=0+0.5 i=0.5 i\)
\(z_{2}=z_{1}^{2}+0.5 i=(0.5 i)^{2}+0.5 i=-0.25+0.5 i\)
\(z_{3}=z_{2}^{2}+0.5 i=(-0.25+0.5 i)^{2}+0.5 i=-0.1875+0.25 i\)
\(z_{4}=z_{3}^{2}+0.5 i=(-0.1875+0.25 i)^{2}+0.5 i=-0.02734+0.40625 i\)
While not definitive with this few iterations, it does appear that this value is remaining small, suggesting that \(0.5 i\) is part of the Mandelbrot set.
Determine if \(c=0.4+0.3 i\) is part of the Mandelbrot set.
- Answer
-
\(z_{1}=z_{0}^{2}+0.4+0.3 i=0+0.4+0.3 i=0.4+0.3 i\)
\(z_{2}=z_{1}^{2}+0.4+0.3 i=(0.4+0.3 i)^{2}+0.4+0.3 i = 0.47+0.54 i\)
\(z_{3}=z_{2}^{2}+0.5 i=(-0.25+0.5 i)^{2}+0.5 i=-0.1875+0.25 i\)
\(z_{4}=z_{3}^{2}+0.5 i=(-0.1875+0.25 i)^{2}+0.5 i=-0.02734+0.40625 i\)
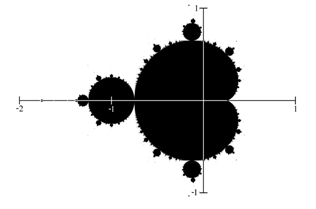If all complex numbers are tested, and we plot each number that is in the Mandelbrot set on the complex plane, we obtain the shape to the right[1].
The boundary of this shape exhibits quasi-self-similarity, in that portions look very similar to the whole.
In addition to coloring the Mandelbrot set itself black, it is common to the color the points in the complex plane surrounding the set. To create a meaningful coloring, often people count the number of iterations of the recursive sequence that are required for a point to get further than 2 units away from the origin. For example, using \(c=1+i\) above, the sequence was distance 2 from the origin after only two recursions.
For some other numbers, it may take tens or hundreds of iterations for the sequence to get far from the origin. Numbers that get big fast are colored one shade, while colors that are slow to grow are colored another shade. For example, in the image below[2], light blue is used for numbers that get large quickly, while darker shades are used for numbers that grow more slowly. Greens, reds, and purples can be seen when we zoom in – those are used for numbers that grow very slowly.
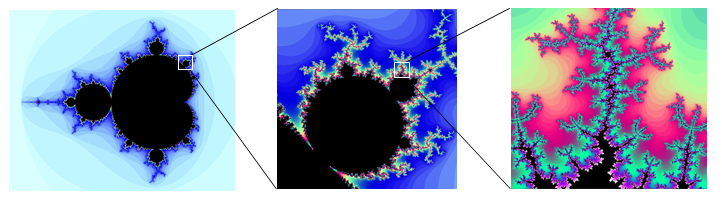
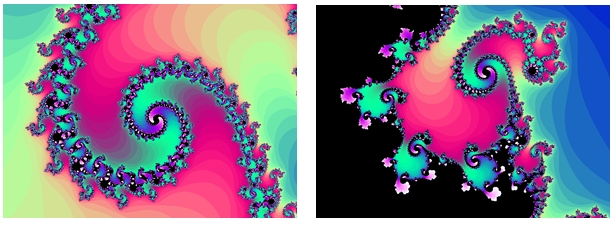
The Mandelbrot set, for having such a simple definition, exhibits immense complexity. Zooming in on other portions of the set yields fascinating swirling shapes.
[1] en.Wikipedia.org/wiki/File:Mandelset_hires.png
[2] This series was generated using Scott’s Mandelbrot Set Explorer