1.6.4.8: Inside R
( \newcommand{\kernel}{\mathrm{null}\,}\)
Vectors in numeric, logical or character modes and factors are enough to represent simple data. However, if the data is structured and/or variable, there is frequently a need for more complicated R objects: matrices, lists and data frames.
Matrices
Matrix is a popular way of presenting tabular data. There are two important things to know about them in R. First, they may have various dimensions. And second—there are, in fact, no true matrices in R.
We begin with the second statement. Matrix in R is just a specialized type of vector with additional attributes that help to identify values as belonging to rows and columns. Here we create the simple 2×2 matrix from the numerical vector:
Code 1.6.4.8.1 (R):
As str() command reveals, objects m and ma are very similar. What is different is the way they are presented on the screen.
Equality of matrices and vectors in even more clear in the next example:
Code 1.6.4.8.2 (R):
In looks like a trick but underlying reason is simple. We assign attribute dim (“dimensions”, size) to the vector mb and state the value of the attribute as c(2, 2), as 2 rows and 2 columns.
Why are matrices mb and ma different?
Another popular way to create matrices is binding vectors as columns or rows with cbind() and rbind(). Related command t() is used to transpose the matrix, turn it clockwise by 90∘.
To index a matrix, use square brackets:
Code 1.6.4.8.3 (R):
The rule here is simple: within brackets, first goes first dimension (rows), and second to columns. So to index, use matrix[rows, columns]. The same rule is applicable to data frames (see below).
Empty index is equivalent to all values:
Code 1.6.4.8.4 (R):
Common ways of indexing matrix do not allow to select diagonal, let alone L-shaped (“knight’s move”) or sparse selection. However, R will satisfy even these exotic needs. Let us select the diagonal values of ma:
Code 1.6.4.8.5 (R):
(Here mi is an indexing matrix. To index 2-dimensional object, it must have two columns. Each row of indexing matrix describes position of the element to select. For example, the second row of mi is equivalent of [2, 2]. As an alternative, there is diag() command but it works only for diagonals.)
Much less exotic is the indexing with logical matrix. We already did similar indexing in the example of missing data imputation. This is how it works in matrices:
Code 1.6.4.8.6 (R):
Since matrices are vectors, all elements of matrix must be of the same mode: either numerical, or character, or logical. If we change mode of one element, the rest of them will change automatically:
Code 1.6.4.8.7 (R):
Two-dimensional matrices are most popular, but there are also multidimensional arrays:
Code 1.6.4.8.8 (R):
(Instead of attr(..., "dim") we used analogous dim(...) command.)
m3 is an array, “3D matrix”. It cannot be displayed as a single table, and R returns it as a series of tables. There are arrays of higher dimensionality; for example, the bui db">Titatic is the 4D array. To index arrays, R requires same square brackets but with three or more elements within.
Lists
List is essentially the collection of anything:
Code 1.6.4.8.9 (R):
Here we see that list is a composite thing. Vectors and matrices may only include elements of the same type while lists accommodate anything, including other lists.
List elements could have names:
Code 1.6.4.8.10 (R):
Names feature is not unique to lists as many other types of R objects could also have named elements. Values inside vectors, and rows and columns of matrices can have their own unique names:
Code 1.6.4.8.11 (R):
>
>
Rick Amanda Peter Alex Kathryn Ben George
69 68 93 87 59 82 72
>
col1 col2
row1 1 2
row2 3 4
To remove names, use:
Code 1.6.4.8.12 (R):
Let us now to index a list. As you remember, we extracted elements from vectors with square brackets:
Code 1.6.4.8.13 (R):
For matrices/arrays, we used several arguments, in case of two-dimensional ones they are row and column numbers:
Code 1.6.4.8.14 (R):
Now, there are at least three ways to get elements from lists. First, we may use the same square brackets:
Code 1.6.4.8.15 (R):
Here the resulting object is also a list. Second, we may use double square brackets:
Code 1.6.4.8.16 (R):
After this operation we obtain the content of the sub-list, object of the type it had prior to joining into the list. The first object in this example is a character vector, while the fifth is itself a list.
Metaphorically, square brackets take egg out of the basket whereas double square brackets will also shell it.
Third, we may create names for the elements of the list and then call these names with dollar sign:
Code 1.6.4.8.17 (R):
Dollar sign is a syntactic sugar that allows to write l$first instead of more complicated l. That last R piece might be regarded as a fourth way to index list, with character vector of names.
Now consider the following example:
Code 1.6.4.8.18 (R):
This happens because dollar sign (and default [[ too) allow for partial matching in the way similar to function arguments. This saves typing time but could potentially be dangerous.
With a dollar sign or character vector, the object we obtain by indexing retains its original type, just as with double square bracket. Note that indexing with dollar sign works only in lists. If you have to index other objects with named elements, use square brackets with character vectors:
Code 1.6.4.8.19 (R):
> names(w) <- c("Rick", "Amanda", "Peter", "Alex", "Kathryn",
+ "Ben", "George")
>
Jenny
68
Lists are so important to learn because many functions in Rstore their output as lists:
Code 1.6.4.8.20 (R):
Therefore, if we want to extract any piece of the output (like p-value, see more in next chapters), we need to use the list indexing principles from the above:
Code 1.6.4.8.21 (R):
Data frames
Now let us turn to the one most important type of data representation, data frames. They bear the closest resemblance with spreadsheets and its kind, and they are most commonly used in R. Data frame is a “hybrid”, “chimeric” type of R objects, unidimensional list of same length vectors. In other words, data frame is a list of vectors-columns[1].
Each column of the data frame must contain data of the same type (like in vectors), but columns themselves may be of different types (like in lists). Let us create a data frame from our existing vectors:
Code 1.6.4.8.22 (R):
(It was not absolutely necessary to enter row.names() since our w object could still retain names and they, by rule, will become row names of the whole data frame.)
This data frame represents data in short form, with many columns-features. Long form of the same data could, for example, look like:
Rick weight 69
Rick height 174.0
Rick size L
Rick sex male
Amanda weight 68
...
In long form, features are mixed in one column, whereas the other column specifies feature id. This is really useful when we finally come to the two-dimensional data analysis.
Commands row.names() or rownames() specify names of data frame rows (objects). For data frame columns (variables), use names() or colnames().
Alternatively, especially if objects w, x, m.o, or sex.f are for some reason absent from the workspace, you can type:
Code 1.6.4.8.23 (R):
... and then immediately check the structure:
Code 1.6.4.8.24 (R):
Since the data frame is in fact a list, we may successfully apply to it all indexing methods for lists. More then that, data frames available for indexing also as two-dimensional matrices:
Code 1.6.4.8.25 (R):
To be absolutely sure that any of two these methods output the same, run:
Code 1.6.4.8.26 (R):
To select several columns (all these methods give same results):
Code 1.6.4.8.27 (R):
(Three of these methods work also for this data frame rows. Try all of them and find which are not applicable. Note also that negative selection works only for numerical vectors; to use several negative values, type something like d[, -c(2:4)]. Think why the colon is not enough and you need c() here.)
Among all these ways, the most popular is the dollar sign and square brackets (Figure 1.6.4.8.1). While first is shorter, the second is more universal.
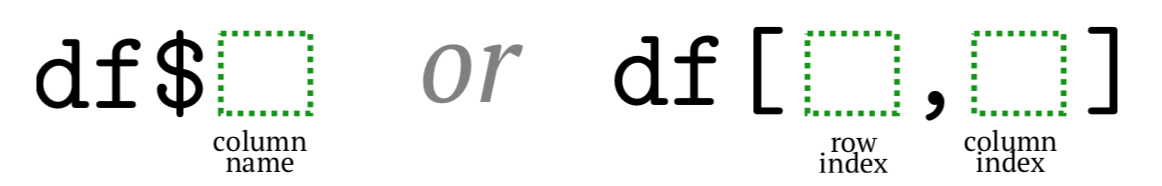 Figure 1.6.4.8.1 Two most important ways to select from data frame.
Figure 1.6.4.8.1 Two most important ways to select from data frame.
Selection by column indices is easy and saves space but it requires to remember these numbers. Here could help the Str() command (note the uppercase) which replaces dollar signs with column numbers (and also indicates with star* sign the presence of NAs, plus shows row names if they are not default):(see Code 1.6.4.8.24 (R):)
'data.frame': 7 obs. of 4 variables:
1 weight: int 69 68 93 87 59 82 72
2 height: num 174 162 188 192 165 ...
3 size : Ord.factor w/ 5 levels "S"<"M"<"L"<"XL"<..: 3 1 4
4 sex : Factor w/ 2 levels "female","male": 2 1 2 2 1 2 2
row.names [1:7] "Rick" "Amanda" "Peter" "Alex" "Kathryn" ...
Now, how to make a subset, select several objects (rows) which have particular features? One way is through logical vectors. Imagine that we are interesting only in the values obtained from females:
Code 1.6.4.8.28 (R):
(To select only rows, we used the logical expression d$sex==female before the comma.)
By itself, the above expression returns a logical vector:
Code 1.6.4.8.29 (R):
This is why R selected only the rows which correspond to TRUE: 2nd and 5th rows. The result is just the same as:
Code 1.6.4.8.30 (R):
Logical expressions could be used to select whole rows and/or columns:
Code 1.6.4.8.31 (R):
It is also possible to apply more complicated logical expressions:
Code 1.6.4.8.32 (R):
(Second example shows how to compare with several character values at once.)
If the process of selection with square bracket, dollar sign and comma looks too complicated, there is another way, with subset() command:
Code 1.6.4.8.33 (R):
However, “classic selection” with [ is preferable (see the more detailed explanation in ?subset).
Selection does not only extract the part of data frame, it also allows to replace existing values:
Code 1.6.4.8.34 (R):
(Now weight is in pounds.)
Partial matching does not work with the replacement, but there is another interesting effect:
Code 1.6.4.8.35 (R):
(A bit mysterious, is not it? However, rules are simple. As usual, expression works from right to left. When we called d.new$he on the right, independent partial matching substituted it with d.new$height and converted centimeters to feet. Then replacement starts. It does not understand partial matching and therefore d.new$he on the left returns NULL. In that case, the new column (variable) is silently created. This is because subscripting with $ returns NULL if subscript is unknown, creating a powerful method to add columns to the existing data frame.)
Another example of “data frame magic” is recycling. Data frame accumulates shorter objects if they evenly fit the data frame after being repeated several times:
Code 1.6.4.8.36 (R):
The following table (Table 1.6.4.8.1) provides a summary of R subscripting with “[”:
| subscript | effect positive numeric |
| vector | selects items with those indices negative numeric |
| vector | selects all but those indices character |
| vector | selects items with those names (or dimnames) logical |
| vector | selects the TRUE (and NA) items |
| missing | selects all |
Table 1.6.4.8.1 Subscription with “[”.
Command sort() does not work for data frames. To sort values in a d data frame, saying, first with sex and then with height, we have to use more complicated operation:
Code 1.6.4.8.37 (R):
The order() command creates a numerical, not logical, vector with the future order of the rows:
Code 1.6.4.8.38 (R):
Use order() to arrange the columns of the d matrix in alphabetic order.
Overview of data types and modes
This simple table (Table 1.6.4.8.2) shows the four basic R objects:
| linear | rectangular | |
| all the same type | vector | matrix |
| mixed type | list | data frame |
Table 1.6.4.8.2 Basic ojects.
(Most, but not all, vectors are also atomic, check it with is.atomic().)
You must know the type (matrix, data frame etc.) and mode (numerical, character etc.) of object you work with. Command str() is especially good for that.
If any procedure wants object of some specific mode or type, it is usually easy to convert into it with as.<something>() command.
Sometimes, you do not need the conversion at all. For example, matrices are already vectors, and all data frames are already lists (but the reverse is not correct!). On the next page, there is a table (Table 1.6.4.8.3) which overviews R internal data types and lists their most important features.
| Data type and mode | What is it? | How to subset? | How to convert? |
| Vector: numeric, character, or logical | Sequence of numbers, character strings, or TRUE/FALSE. Made with c(), colon operator :, scan(), rep(), seq() etc. | With numbers like vector[1].With names (if named) like vector["Name"].With logical expression like vector[vector > 3]. | matrix(), rbind(), cbind(), t() to matrix; as.numeric() and as.character() convert modes |
| Vector: factor | Way of encoding vectors. Has values and levels (codes), and sometimes also names. | Just like vector. Factors could be also re-leveled or ordered with factor(). | c() to numeric vector, droplevels() removes unused levels |
| Matrix | Vector with two dimensions. All elements must be of the same mode. Made with matrix(), cbind() etc. | matrix[2, 3] is a cell; matrix[2:3, ] or matrix[matrix[, 1] > 3, ] rows; matrix[, 3] column | Matrix is a vector; c() or dim(...) <- NULL removes dimensions |
| List | Collection of anything. Could be nested (hierarchical). Made with list(). Most of statistical outputs are lists. | list[2] or (if named) list["Name"] is element; list or list$Name content of the element | unlist() to vector, data.frame() only if all elements have same length |
| Data frame | Named list of anything of same lengths but (possibly) different modes. Data could be short (ids are columns) and/or long (ids are rows). Made with read.table(), data.frame() etc. | Like matrix: df[2, 3] (with numbers) or df[, "Name"] (with names) or df[df[, 1] > 3, ] (logical).Like list: df[1] or df$Name.Also possible: subset(df, Name > 3) | Data frame is a list; matrix() converts to matrix (modes will be unified); t() transposes and converts to matrix |
Table 1.6.4.8.3 Overview of the most important R internal data types and ways to work with them.
References
1. In fact, columns of data frames might be also matrices or other data frames, but this feature is rarely useful.

