3A.5: Solve Applications with Systems of Equations

Last updated
Save as PDF

Page ID: 33589

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

By the end of this section, you will be able to:

Solve direct translation applications
Solve geometry applications
Solve uniform motion applications
Solve mixture applications
Solve interest applications
Solve applications of cost and revenue functions

Solve Direct Translation Applications

Systems of linear equations are very useful for solving applications. Some people find setting up word problems with two variables easier than setting them up with just one variable. To solve an application, we’ll first translate the words into a system of linear equations. Then we will decide the most convenient method to use, and then solve the system.

SOLVE APPLICATIONS WITH SYSTEMS OF EQUATIONS.

Read the problem. Make sure all the words and ideas are understood.
Identify what we are looking for.
Name what we are looking for. Choose variables to represent those quantities.
Translate into a system of equations.
Solve the system of equations using good algebra techniques.
Check the answer in the problem and make sure it makes sense.
Answer the question with a complete sentence.

We solved number problems with one variable earlier. Let’s see how differently it works using two variables.

Example $\PageIndex{1}$

The sum of two numbers is zero. One number is nine less than the other. Find the numbers.

Solution

Step 1. Read the problem.
Step 2. Identify what we are looking for.	We are looking for two numbers.
Step 3. Name what we are looking for.	Let $n= \text{the first number} $. $m= \text{the second number} $
Step 4. Translate into a system of equations.	The sum of two numbers is zero.
	$.$
	One number is nine less than the other.
	$.$
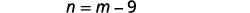The system is:	$.$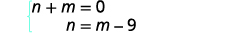
Step 5. Solve the system of equations. We will use substitution since the second equation is solved for n.
Substitute m − 9 for n in the first equation.	$.$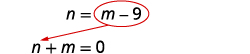
Solve for m.	$.$
	$.$
	$.$
Substitute $m=\frac{9}{2}$ into the second equation and then solve for n.	$.$
	$.$
	$.$
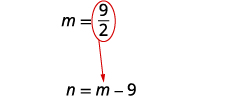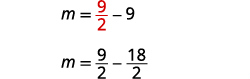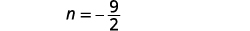Step 6. Check the answer in the problem.	Do these numbers make sense in the problem? We will leave this to you!
Step 7. Answer the question.	The numbers are $\frac{9}{2}$ and $−\frac{9}{2}$.

$try-it.png$ $\PageIndex{1A}$

The sum of two numbers is 10. One number is 4 less than the other. Find the numbers.

Answer: $3, 7$

$try-it.png$ $\PageIndex{1B}$

The sum of two numbers is $−6$. One number is 10 less than the other. Find the numbers.

Answer: $2, −8$

Example $\PageIndex{2}$

Indira has been offered two options for her salary as a trainer at the gym. Option A would pay her $25,000 plus $15 for each training session. Option B would pay her $$10,000+$40$ for each training session. How many training sessions would make the salary options equal?

Solution

Step 1. Read the problem.
Step 2. Identify what we are looking for.	We are looking for the number of training sessions that would make the pay equal.
Step 3. Name what we are looking for.	Let s= Indira’s salary when the 2 salary options are equal, n= the number of training sessions.
Step 4. Translate into a system of equations.	Option A would pay her $25,000 plus $15 for each training session.
	$.$
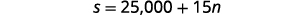	Option B would pay her $10,000 + $40 for each training session.
	$.$
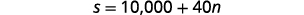The system is shown.	$.$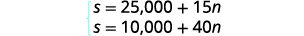
Step 5. Solve the system of equations. We will use substitution.	$.$
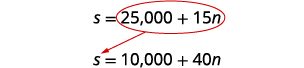Substitute 25,000 +15n for s in the second equation.	$.$
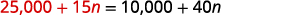Solve for n.	$.$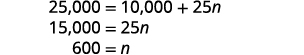
Step 6. Check the answer.	Are 600 training sessions a year reasonable? Are the two options equal when n = 600?
Step 7. Answer the question.	The salary options would be equal for 600 training sessions.

$try-it.png$ $\PageIndex{2A}$

Tatyana has been offered positions by two insurance companies. The first company pays a salary of $12,000 plus a commission of $100 for each policy sold. The second pays a salary of $20,000 plus a commission of $50 for each policy sold. How many policies would need to be sold to make the total pay the same?

Answer: 160 policies

$try-it.png$ $\PageIndex{2B}$

Hyungjoo currently sells suits for company A at a salary of $22,000 plus a $10 commission for each suit sold. Company B offers him a position with a salary of $28,000 plus a $4 commission for each suit sold. How many suits would Hyungjoo need to sell for the options to be equal?

Answer: 1,000 suits

As you solve each application, remember to analyze which method of solving the system of equations would be most convenient.

Example $\PageIndex{3}$

Translate to a system of equations and then solve:

When Jenna spent 10 minutes on the elliptical trainer and then did circuit training for 20 minutes, her fitness app says she burned 278 calories. When she spent 20 minutes on the elliptical trainer and 30 minutes circuit training she burned 473 calories. How many calories does she burn for each minute on the elliptical trainer? How many calories for each minute of circuit training?

Solution

Step 1. Read the problem.
Step 2. Identify what we are looking for.	We are looking for the number of calories burned per minute on the elliptical trainer and each minute of circuit training.
Step 3. Name what we are looking for.	Let e= number of calories burned per minute on the elliptical trainer, c= number of calories burned per minute while circuit training.
Step 4. Translate into a system of equations.	10 minutes on the elliptical and circuit training for 20 minutes, burned 278 calories
	$.$
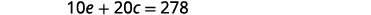	20 minutes on the elliptical and 30 minutes of circuit training burned 473 calories
	$.$
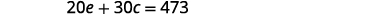The system is:	$.$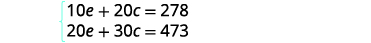
Step 5. Solve the system of equations.
Multiply the first equation by −2 to get opposite coefficients of e.	$.$
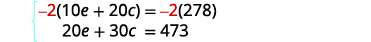Simplify and add the equations. Solve for c.	$.$
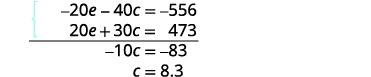Substitute c = 8.3 into one of the original equations to solve for e.	$.$
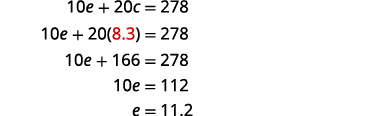Step 6. Check the answer in the problem.	Check the math on your own.
	$.$
Step 7. Answer the question.	Jenna burns 8.3 calories per minute circuit training and 11.2 calories per minute while on the elliptical trainer.

$try-it.png$ $\PageIndex{3A}$

Translate to a system of equations and then solve:

Mark went to the gym and did 40 minutes of Bikram hot yoga and 10 minutes of jumping jacks. He burned 510 calories. The next time he went to the gym, he did 30 minutes of Bikram hot yoga and 20 minutes of jumping jacks burning 470 calories. How many calories were burned for each minute of yoga? How many calories were burned for each minute of jumping jacks?

Answer: Mark burned 11 calories for each minute of yoga and 7 calories for each minute of jumping jacks.

$try-it.png$ $\PageIndex{3B}$

Translate to a system of equations and then solve:

Erin spent 30 minutes on the rowing machine and 20 minutes lifting weights at the gym and burned 430 calories. During her next visit to the gym she spent 50 minutes on the rowing machine and 10 minutes lifting weights and burned 600 calories. How many calories did she burn for each minutes on the rowing machine? How many calories did she burn for each minute of weight lifting?

Answer: Erin burned 11 calories for each minute on the rowing machine and 5 calories for each minute of weight lifting.

Solve Geometry Applications

We will now solve geometry applications using systems of linear equations. We will need to define complementary angles and supplementary angles.

definition: COMPLEMENTARY AND SUPPLEMENTARY ANGLES

Two angles are complementary if the sum of the measures of their angles is 90 degrees.

Two angles are supplementary if the sum of the measures of their angles is 180 degrees

If two angles are complementary, we say that one angle is the complement of the other.

If two angles are supplementary, we say that one angle is the supplement of the other.

Example $\PageIndex{4}$

Translate to a system of equations and then solve.

The difference of two complementary angles is 26 degrees. Find the measures of the angles.

Solution

\(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what we are looking for.}} &{\text{We are looking for the measure of each}} \\ {} &{\text{angle.}} \\ {\textbf{Step 3. Name }\text{what we are looking for.}} &{\text{Let } x= \text{ the measure of the first angle,}} \\ {} &{\hspace{3mm} y= \text{ the measure of the second angle.}} \\ {\textbf{Step 4. Translate }\text{into a system of}} &{\text{The angles are complementary.}} \\ {\text{equations.}} &{\hspace{15mm} x+y=90} \\ {} &{\text{The difference of the two angles is 26}} \\ {} &{\text{degrees.}} \\ {} &{\hspace{15mm} x−y=26} \\ {} &{} \\ {} &{} \\ {\text{The system is shown.}} &{\hspace{15mm} \left\{ \begin{array} {l} x+y=90 \\ x−y=26 \end{array} \right. } \\ {} &{} \\ {} &{} \\ {\textbf{Step 5. Solve }\text{the system of equations} } &{\hspace{15mm} \left\{ \begin{array} {l} x+y=90 \\ \underline{x−y=26} \end{array} \right. } \\ {\text{by elimination.}} &{\hspace{21mm} 2x\hspace{4mm}=116} \\ {} &{\hspace{28mm} x=58} \\ {} &{} \\ {} &{} \\ {\text{Substitute }x=58\text{ into the first equation.}} &{\hspace{15mm} x+y=90} \\ {} &{\hspace{14mm} 58+y=90} \\ {} &{\hspace{22mm} y=32} \\ {\textbf{Step 6. Check }\text{the answer in the problem.}} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\hspace{15mm} 58+32=90\checkmark} &{} \\ {\hspace{15mm} 58−32=26\checkmark} &{} \\ {\textbf{Step 7. Answer }\text{the question.}} &{\text{The angle measures are 58 and 32 degrees.}} \end{array} \)

$try-it.png$ $\PageIndex{4A}$

Translate to a system of equations and then solve:

The difference of two complementary angles is 20 degrees. Find the measures of the angles.

Answer: The angle measures are $55^{\circ}$ and $35^{\circ}$.

$try-it.png$ $\PageIndex{4B}$

Translate to a system of equations and then solve:

The difference of two complementary angles is 80 degrees. Find the measures of the angles.

Answer: The angle measures are 5 degrees and 85 degrees.

In the next example, we remember that the measures of supplementary angles add to 180 degrees.

Example $\PageIndex{5}$

Translate to a system of equations and then solve:

Two angles are supplementary. The measure of the larger angle is twelve degrees less than five times the measure of the smaller angle. Find the measures of both angles.

Solution

Step 1. Read the problem.
Step 2. Identify what we are looking for.	We are looking for measure of each angle.
Step 3. Name what we are looking for.	Let x= the measure of the first angle. y= the measure of the second angle
Step 4. Translate into a system of equations.	The angles are supplementary.
	$.$
	The larger angle is twelve less than five times the smaller angle.
	$.$
The system is shown: Step 5. Solve the system of equations by substitution.	$.$
Substitute 5x − 12 for y in the first equation. Solve for x.	$.$
Substitute 32 for x in the second equation, then solve for y.	$.$ $.$
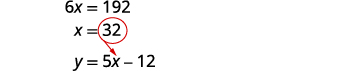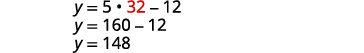Step 6. Check the answer in the problem.
Step 7. Answer the question.	The angle measures are 148 and 32 degrees.

$try-it.png$ $\PageIndex{5A}$

Translate to a system of equations and then solve:

Two angles are supplementary. The measure of the larger angle is 12 degrees more than three times the smaller angle. Find the measures of the angles.

Answer: The angle measures are 42 degrees and 138 degrees.

$try-it.png$ $\PageIndex{5B}$

Translate to a system of equations and then solve:

Two angles are supplementary. The measure of the larger angle is 18 less than twice the measure of the smaller angle. Find the measures of the angles.

Answer: The angle measures are $66^{\circ}$ and $114^{\circ}$.

Recall that the angles of a triangle add up to 180 degrees. A right triangle has one angle that is 90 degrees. What does that tell us about the other two angles? In the next example we will be finding the measures of the other two angles.

Example $\PageIndex{6}$

The measure of one of the small angles of a right triangle is ten more than three times the measure of the other small angle. Find the measures of both angles.

Solution

We will draw and label a figure.

Step 1. Read the problem.	$.$
Step 2. Identify what you are looking for.	We are looking for the measures of the angles.
Step 3. Name what we are looking for.	Let a= the measure of the first angle. b= the measure of the second angle
Step 4. Translate into a system of equations.	The measure of one of the small angles of a right triangle is ten more than three times the measure of the other small angle.
	$.$
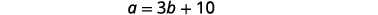	The sum of the measures of the angles of a triangle is 180.
	$.$
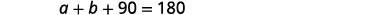The system is shown.	$.$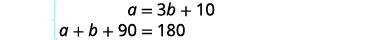
Step 5. Solve the system of equations. We will use substitution since the first equation is solved for a.	$.$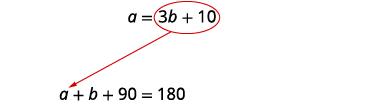
Substitute 3b+10 for a in the second equation.	$.$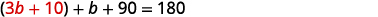
Solve for b.	$.$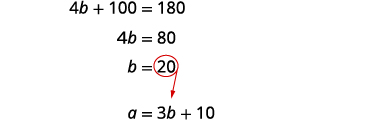
Substitute b=20 into the first equation and then solve for a.	$.$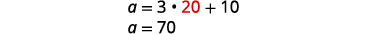
Step 6. Check the answer in the problem.	We will leave this to you!
Step 7. Answer the question.	The measures of the small angles are 20 and 70 degrees.

$try-it.png$ $\PageIndex{6A}$

The measure of one of the small angles of a right triangle is 2 more than 3 times the measure of the other small angle. Find the measure of both angles.

Answer: $22^{\circ}, 68^{\circ}$

$try-it.png$ $\PageIndex{6B}$

The measure of one of the small angles of a right triangle is 18 less than twice the measure of the other small angle. Find the measure of both angles.

Answer: $36^{\circ}, 54^{\circ}$

Often it is helpful when solving geometry applications to draw a picture to visualize the situation.

Example $\PageIndex{7}$

Translate to a system of equations and then solve:

Hassan has 125 feet of fencing to enclose the part of his backyard adjacent to his house. He will only need to fence around three sides, because the fourth side will be the wall of the house. He wants the length of the fenced yard (parallel to the house wall) to be 5 feet more than four times as long as the width. Find the length and the width.

Solution

Step 1. Read the problem.
Step 2. Identify what you are looking for.	We are looking for length and width of the fenced yard.
	$.$
Step 3. Name what we are looking for.	Let L= the length of the fenced yard. W= the width of the fenced yard
Step 4. Translate into a system of equations.	One lenth and two widths equal 125.
	$.$
	The length will be 5 feet more than four times the width.
	$.$
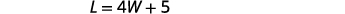The system is shown. Step 5. Solve The system of equations by substitution.	$.$
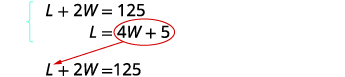Substitute L = 4W + 5 into the first equation, then solve for W.	$.$
	$.$
Substitute 20 for W in the second equation, then solve for L.	$.$
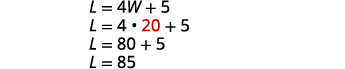Step 6. Check the answer in the problem.	$.$
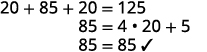Step 7. Answer the equation.	The length is 85 feet and the width is 20 feet.

$try-it.png$ $\PageIndex{7A}$

Translate to a system of equations and then solve:

Mario wants to put a fence around the pool in his backyard. Since one side is adjacent to the house, he will only need to fence three sides. There are two long sides and the one shorter side is parallel to the house. He needs 155 feet of fencing to enclose the pool. The length of the long side is 10 feet less than twice the width. Find the length and width of the pool area to be enclosed.

Answer: The length is 60 feet and the width is 35 feet.

$try-it.png$ $\PageIndex{7B}$

Translate to a system of equations and then solve:

Alexis wants to build a rectangular dog run in her yard adjacent to her neighbor’s fence. She will use 136 feet of fencing to completely enclose the rectangular dog run. The length of the dog run along the neighbor’s fence will be 16 feet less than twice the width. Find the length and width of the dog run.

Answer: The length is 60 feet and the width is 38 feet.

Solve Uniform Motion Applications

We used a table to organize the information in uniform motion problems when we introduced them in Section 2.5. We’ll continue using the table here. The basic equation was $D=rt$ where D is the distance traveled, r is the rate, and t is the time.

Our first example of a uniform motion application will be for a situation similar to some we have already seen, but now we can use two variables and two equations.

Example $\PageIndex{8}$

Translate to a system of equations and then solve:

Joni left St. Louis on the interstate, driving west towards Denver at a speed of 65 miles per hour. Half an hour later, Kelly left St. Louis on the same route as Joni, driving 78 miles per hour. How long will it take Kelly to catch up to Joni?

Solution

A diagram is useful in helping us visualize the situation.

$.$

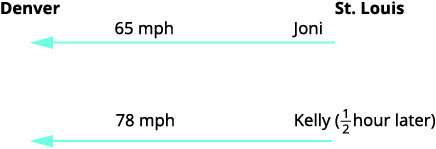
Identify and name what we are looking for. A chart will help us organize the data. We know the rates of both Joni and Kelly, and so we enter them in the chart. We are looking for the length of time Kelly, k, and Joni, j, will each drive.

$.$

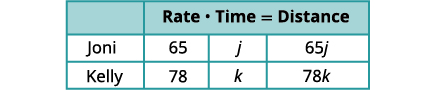
Since $D=r·t$ we can fill in the Distance column.

Translate into a system of equations.

To make the system of equations, we must recognize that Kelly and Joni will drive the same distance. So,

$\hspace{85mm} 65j=78k \nonumber $

Also, since Kelly left later, her time will be $\frac{1}{2}$ hour less than Joni’s time. So,

$ \hspace{105mm} k=j-\frac{1}{2} \nonumber $

\(\begin{array} {ll} {\text{Now we have the system.}} &{\left\{ \begin{array} {l} k=j−\frac{1}{2} \\ 65j=78k \end{array} \right.} \\ {\textbf{Solve }\text{the system of equations by substitution.}} &{} \\ {} &{} \\ {\text{Substitute }k=j−12\text{ into the second equation,}} &{} \\ {\text{then solve for }j.} &{} \\ {} &{65j=78k} \\ {} &{65j=78(j−\frac{1}{2})} \\ {} &{65j=78j−39} \\ {} &{−13j=−39} \\ {} &{j=3} \\{\begin{array} {l} {\text{To find Kelly’s time, substitute }j=3 \text{ into the first}} \\ {\text{equation, then solve for }k.} \end{array} } &{k=j−\frac{1}{2}} \\ {} &{k=3−\frac{1}{2} } \\ {} &{k=\frac{5}{2} \text{ or } k=2\frac{1}{2}} \\ {\textbf{Check }\text{the answer in the problem.}} &{} \\ {\begin{array} {lllll} {\text{Joni}} &{3 \text{ hours}} &{(65\text{ mph})} &= &{195\text{ miles}} \\ {\text{Kelly}} &{2\frac{1}{2} \text{ hours}} &{(78\text{ mph})} &= &{195\text{ miles}} \end{array}} &{} \\ {\text{Yes, they will have traveled the same distance}} &{} \\{\text{when they meet.}} &{} \\ {\textbf{Answer }\text{the question.}} &{} \\ {} &{\text{Kelly will catch up to Joni in}} \\ {} &{2\frac{1}{2}\text{ hours. By then, Joni will}} \\ {} &{\text{have traveled }3 \text{ hours.}} \\ \end{array}\)

$try-it.png$ $\PageIndex{8A}$

Translate to a system of equations and then solve:

Marvin left Detroit on the interstate driving south towards Orlando at a speed of 60 miles per hour. Stevie left Detroit 1 hour later traveling at a speed of 75 miles per hour, following the same route as Marvin. How long will it take Stevie to catch Marvin?

Answer: It will take Stevie 4 hours to catch Marvin.

$try-it.png$ $\PageIndex{8B}$

Translate to a system of equations and then solve:

Michael left his mother’s house traveling at an average speed of 36 miles per hour. His sister Janet left 15 minutes $(\frac{1}{4} \text{ hour})$ later traveling the same route at an average speed of 42 miles per hour. How long before Janet catches up to Michael?

Answer: It will take Janet $112$ hours to catch up to Michael.

Many real-world applications of uniform motion arise because of the effects of currents—of water or air—on the actual speed (or rate) of a vehicle. Cross-country airplane flights in the United States generally take longer going west than going east because of the prevailing wind currents.

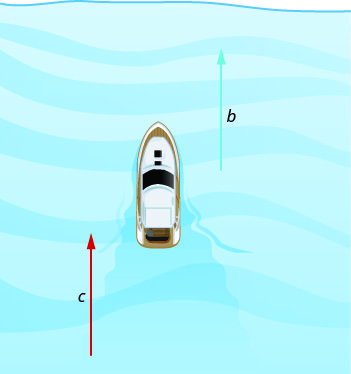
Let’s take a look at a boat travelling on a river. Depending on which way the boat is going, the current of the water is either slowing it down or speeding it up.

The images below show how a river current affects the speed at which a boat is actually travelling. We’ll call the speed of the boat in still water b and the speed of the river current c.

The boat is going downstream, in the same direction as the river current. The current helps push the boat, so the boat’s actual speed is faster than its speed in still water. The actual speed at which the boat is moving is $b+c$.

$Figure shows a boat and two horizontal arrows, both pointing left. The one to the left of the boat is b and the one to the right is c.$

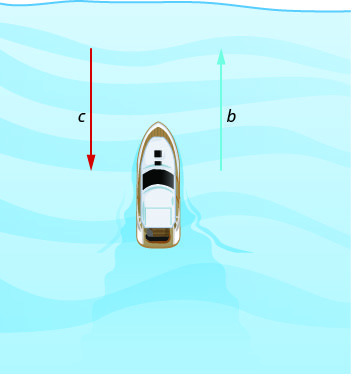
Now, the boat is going upstream, opposite to the river current. The current is going against the boat, so the boat’s actual speed is slower than its speed in still water. The actual speed of the boat is $b−c$.

$Figure shows a boat and two horizontal arrows to its left. One, labeled b, points left and the other, labeled c, points right.$

We’ll put some numbers to this situation in the next example.

Example $\PageIndex{9}$

Translate to a system of equations and then solve.

A river cruise ship travelled 60 miles downstream for 4 hours and then took 5 hours travelling upstream to return to the dock. Find the speed of the ship in still water and the speed of the river current.

Solution

Read the problem.	This is a uniform motion problem and a picture will help us visualize the situation.

Identify what we are looking for.	We are looking for the speed of the ship in still water and the speed of the current.
Name what we are looking for.	Let $s= \text{the rate of the ship in still water,}$ $c= \text{the rate of the current.}$
A chart will help us organize the information. The ship goes downstream and then upstream. Going downstream, the current helps the ship and so the ship's actual rate is s + c. Going upstream, the current slows the ship and so the actual rate is s − c.	$.$
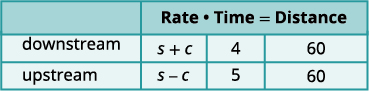Downstream it takes 4 hours. Upstream it takes 5 hours. Each way the distance is 60 miles.
Translate into a system of equations. Since rate times time is distance, we can write the system of equations.	$.$
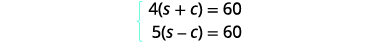Solve the system of equations. Distribute to put both equations in standard form, then solve by elimination.	$.$
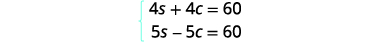Multiply the top equation by 5 and the bottom equation by 4. Add the equations, then solve for s.	$.$
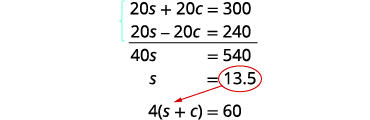Substitute s = 13.5 into of the original equations.	$.$
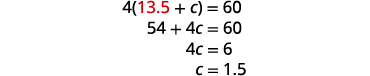Check the answer in the problem. The downstream rate would be $13.5+1.5=15$ mph. In 4 hours the ship would travel $15·4=60$ miles. The upstream rate would be $13.5−1.5=12$ mph. In 5 hours the ship would travel $12·5=60$ miles.
Answer the question.	The rate of the ship is 13.5 mph and the rate of the current is 1.5 mph.

$try-it.png$ $\PageIndex{9}$

Translate to a system of equations and then solve:

A Hudson River boat cruise sailed 120 miles upstream for 12 hours and then took 10 hours to return to the dock. Find the speed of the river boat in still water and the speed of the river current.

Answer: The rate of the boat is 11 mph and the rate of the current is 1 mph.

Wind currents affect airplane speeds in the same way as water currents affect boat speeds. We’ll see this in the next example. A wind current in the same direction as the plane is flying is called a tailwind. A wind current blowing against the direction of the plane is called a headwind.

Example $\PageIndex{10}$

Translate to a system of equations and then solve:

A private jet can fly 1,095 miles in three hours with a tailwind but only 987 miles in three hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Solution

Read the problem.	This is a uniform motion problem and a picture will help us visualize.
	$.$
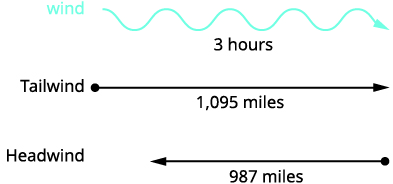Identify what we are looking for.	We are looking for the speed of the jet in still air and the speed of the wind.
Name what we are looking for.	Let j= the speed of the jet in still air, w= the speed of the wind.
A chart will help us organize the information. The jet makes two trips—one in a tailwind and one in a headwind. In a tailwind, the wind helps the jet and so the rate is j + w. In a headwind, the wind slows the jet and so the rate is j ‒ w.	$.$
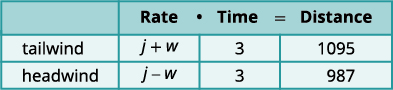Each trip takes 3 hours. In a tailwind the jet flies 1,095 miles. In a headwind the jet flies 987 miles.
Translate into a system of equations. Since rate times time is distance, we get the system of equations.	$.$
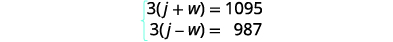Solve the system of equations. Distribute, then solve by elimination. Add, and solve for j.	$.$
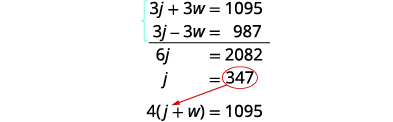Substitute j = 347 into one of the original equations, then solve for w.	$.$
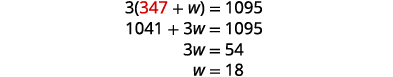Check the answer in the problem. With the tailwind, the actual rate of the jet would be $347+18=365$ mph. In 3 hours the jet would travel $365·3=1,095$ miles Going into the headwind, the jet’s actual rate would be $347−18=329$ mph. In 3 hours the jet would travel $329·3=987$ miles.
Answer the question.	The rate of the jet is 347 mph and the rate of the wind is 18 mph.

$try-it.png$ $\PageIndex{10}$

Translate to a system of equations and then solve:

A small jet can fly 1,325 miles in 5 hours with a tailwind but only 1,035 miles in 5 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Answer: The speed of the jet is 235 mph and the speed of the wind is 30 mph.

Solve Mixture Applications

Mixture applications involve combining two or more quantities. When we solved mixture applications with coins and tickets earlier in Section 2.5, we started by creating a table so we could organize the information. For a coin example with nickels and dimes, the table looked like this:

$This table has 4 columns and two rows. The first column labels each row nickels and dimes. The header labels the columns number times value equals total value.$

Using one variable meant that we had to relate the number of nickels and the number of dimes. We had to decide if we were going to let n be the number of nickels and then write the number of dimes in terms of n, or if we would let d be the number of dimes and write the number of nickels in terms of d.

Now that we know how to solve systems of equations with two variables, we’ll just let n be the number of nickels and d be the number of dimes. We’ll write one equation based on the total value column, like we did before, and the other equation will come from the number column.

For the first example, we’ll do a ticket problem where the ticket prices are in whole dollars, so we won’t need to use decimals just yet.

Example $\PageIndex{11}$

Translate to a system of equations and solve:

A science center sold 1,363 tickets on a busy weekend. The receipts totaled $12,146. How many $12 adult tickets and how many $7 child tickets were sold?

Solution

Step 1. Read the problem.	We will create a table to organize the information.
Step 2. Identify what we are looking for.	We are looking for the number of adult tickets and the number of child tickets sold.
Step 3. Name what we are looking for.	Let $a= \text{the number of adult tickets,}$ $c= \text{the number of child tickets.}$
A table will help us organize the data. We have two types of tickets, adult and child.	Write in a and c for the number of tickets.
Write the total number of tickets sold at the bottom of the Number column.	Altogether 1,363 were sold.
Write the value of each type of ticket in the Value column.	The value of each adult ticket is $12. The value of each child tickets is $7.
The number times the value gives the total value, so the total value of adult tickets is $a·12=12a$, and the total value of child tickets is $c·7=7c$.	Fill in the Total Value column.
Altogether the total value of the tickets was $12,146.	$.$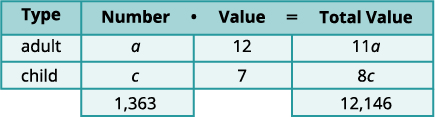
Step 4. Translate into a system of equations.
The Number column and the Total value column give us the system of equations.	$.$
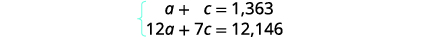We will use the elimination method to solve this system. Multiply the first equation by $−7$.	$.$
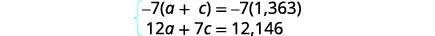Simplify and add, then solve for a.	$.$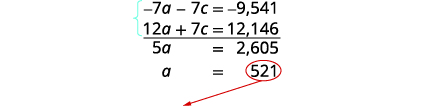
Substitute $a=521$ into the first equation, then solve for c.	$.$
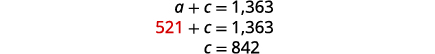Step 6. Check the answer in the problem. 521 adult at $12 per ticket makes $ 6,252 842 child at $7 per ticket makes $58,994 The total receipts are $12,146$\checkmark$
Step 7. Answer the question.	The science center sold 521 adult tickets and 842 child tickets.

$try-it.png$ $\PageIndex{11A}$

Translate to a system of equations and solve:

The ticket office at the zoo sold 553 tickets one day. The receipts totaled $3,936. How many $9 adult tickets and how many $6 child tickets were sold?

Answer: 206 adults, 347 children

$try-it.png$ $\PageIndex{11B}$

Translate to a system of equations and solve:

The box office at a movie theater sold 147 tickets for the evening show, and receipts totaled $1,302. How many $11 adult and how many $8 child tickets were sold?

Answer: 42 adults, 105 children

In the next example, we’ll solve a coin problem. Now that we know how to work with systems of two variables, naming the variables in the ‘number’ column will be easy.

Example $\PageIndex{12}$

Translate to a system of equations and solve:

Juan has a pocketful of nickels and dimes. The total value of the coins is $8.10. The number of dimes is 9 less than twice the number of nickels. How many nickels and how many dimes does Juan have?

Solution

Step 1. Read the problem. We will create a table to organize the information.
Step 2. Identify what we are looking for.	We are looking for the number of nickels and the number of dimes.
Step 3. Name what we are looking for.	Let $n= \text{the number of nickels,}$ $d= \text{the number of dimes.}$
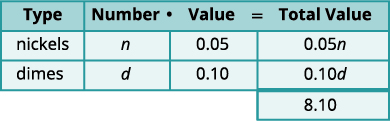
A table will help us organize the data. We have two types of coins, nickels and dimes.	Write n and d for the number of each type of coin.
Fill in the Value column with the value of each type of coin.	The value of each nickel is $0.05. The value of each dime is $0.10.
The number times the value gives the total value, so, the total value of the nickels is $n(0.05)=0.05n$ and the total value of dimes is $d(0.10)=0.10d$. Altogether the total value of the coins is $8.10.	$.$
Step 4. Translate into a system of equations.
The Total Value column gives one equation.	$.$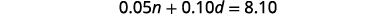
We also know the number of dimes is 9 less than twice the number of nickels.
Translate to get the second equation.	$.$
Now we have the system to solve.	$.$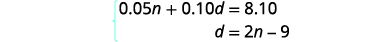
Step 5. Solve the system of equations We will use the substitution method.
Substitute $d=2n−9$ into the first equation.	$.$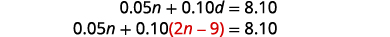
Simplify and solve for n.	$.$
To find the number of dimes, substitute $n=36$ into the second equation.	$.$
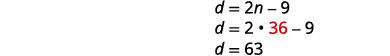Step 6. Check the answer in the problem 63 dimes at $$0.10=$6.30$ 36 nickels at $$0.05=$1.80$ Total $=$8.10\checkmark$
Step 7. Answer the question.	Juan has 36 nickels and 63 dimes.

$try-it.png$ $\PageIndex{12A}$

Translate to a system of equations and solve:

Genice has a handful of quarters and dimes, with a total value of $8.55. The number of quarters is 3 more than twice the number of dimes. How many dimes and how many quarters does she have?

Answer: 13 dimes and 29 quarters

$try-it.png$ $\PageIndex{12B}$

Translate to a system of equations and solve:

Priam has a collection of nickels and quarters, with a total value of $7.30. The number of nickels is six less than three times the number of quarters. How many nickels and how many quarters does he have?

Answer: 19 quarters and 51 nickels

Some mixture applications involve combining foods or drinks. Example situations might include combining raisins and nuts to make a trail mix or using two types of coffee beans to make a blend.

Example $\PageIndex{13}$

Translate to a system of equations and solve:

Alfredo wants to make 20 pounds of trail mix using nuts and chocolate chips. His budget requires that the trail mix costs him $7.60. per pound. Nuts cost $9.00 per pound and chocolate chips cost $2.00 per pound. How many pounds of nuts and how many pounds of chocolate chips should he use?

Solution

Step 1. Read the problem. We will create a table to organize the information.
Step 2. Identify what we are looking for.	We are looking for the number of pounds of nuts and the number of pounds of chocolate chips.
Step 3. Name what we are looking for.	Let $n= \text{the number of pound of nuts,}$ $c= \text{the number of pounds of chips.}$
Alfredo will mix nuts and chocolate chips to get trail mix. Write in n and c for the number of pounds of nuts and chocolate chips.	$.$
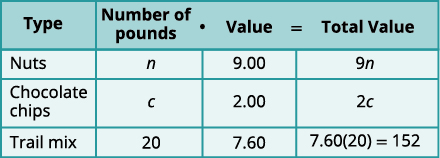There will be 20 pounds of trail mix. Put the price per pound of each item in the Value column. Fill in the last column using $\text{Number}•\text{Value}=\text{Total Value}$
Step 4. Translate into a system of equations. We get the equations from the Number and Total Value columns.	$.$
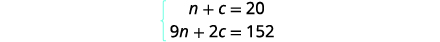Step 5. Solve the system of equations We will use elimination to solve the system. Multiply the first equation by $−2$ to eliminate c.	$.$
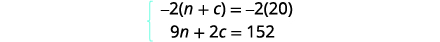Simplify and add. Solve for n.	$.$
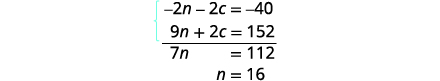To find the number of pounds of chocolate chips, substitute $n=16$ into the first equation, then solve for c.	$.$
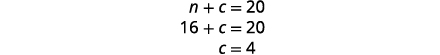Step 6. Check the answer in the problem. $\begin{array} {lll} 16+4 &= &20\checkmark \\ 9·16+2·4 &= &152\checkmark \end{array}$
Step 7. Answer the question.	Alfredo should mix 16 pounds of nuts with 4 pounds of chocolate chips to create the trail mix.

$try-it.png$ $\PageIndex{13}$

Translate to a system of equations and solve:

Sammy has most of the ingredients he needs to make a large batch of chili. The only items he lacks are beans and ground beef. He needs a total of 20 pounds combined of beans and ground beef and has a budget of $3 per pound. The price of beans is $1 per pound and the price of ground beef is $5 per pound. How many pounds of beans and how many pounds of ground beef should he purchase?

Answer: 10 pounds of beans, 10 pounds of ground beef

Another application of mixture problems relates to concentrated cleaning supplies, other chemicals, and mixed drinks. The concentration is given as a percent. For example, a 20% concentration of household cleanser means that 20% of the total amount is cleanser, and the rest is water. To make 35 ounces of a 20% concentration, you mix 7 ounces (20% of 35) of the cleanser with 28 ounces of water.

For these kinds of mixture problems, we’ll use “percent” instead of “value” for one of the columns in our table.

Example $\PageIndex{14}$

Translate to a system of equations and solve:

Sasheena is a lab assistant at her community college. She needs to make 200 milliliters of a 40% solution of sulfuric acid for a lab experiment. The lab has only 25% and 50% solutions in the storeroom. How much should she mix of the 25% and the 50% solutions to make the 40% solution?

Solution

Step 1. Read the problem. A figure may help us visualize the situation, then we will create a table to organize the information.	Sasheena must mix some of the $25\%$ solution and some of the $50\%$ solution together to get $200\space ml$ of the $40\%$ solution.
	$.$
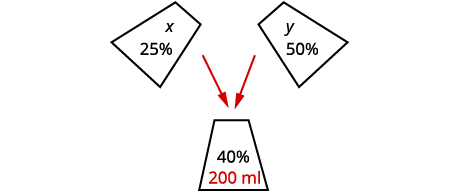Step 2. Identify what we are looking for.	We are looking for how much of each solution she needs.
Step 3. Name what we are looking for.	Let $x= \text{number of ml of } 25\% \text{ solution,}$ $y= \text{number of ml of }50\% \text{ solution.}$
A table will help us organize the data. She will mix x $ml$ of $25%$ with y $ml$ of $50%$ to get $200 \space ml$ of $40%$ solution. We write the percents as decimals in the chart. We multiply the number of units times the concentration to get the total amount of sulfuric acid in each solution.	$.$
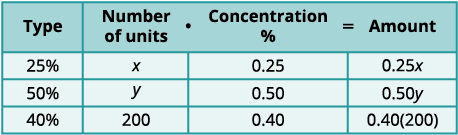Step 4. Translate into a system of equations. We get the equations from the Number column and the Amount column. Now we have the system.	$.$
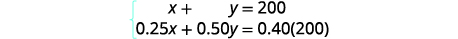Step 5. Solve the system of equations We will solve the system by elimination. Multiply the first equation by $−0.5$ to eliminate y.	$.$
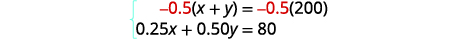Simplify and add to solve for x.	$.$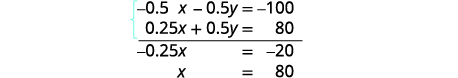
To solve for y, substitute $x=80$ into the first equation.	$.$
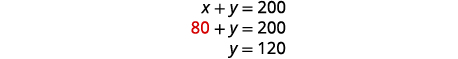Step 6. Check the answer in the problem. $\begin{array} {lll} 80+120 &= &200\checkmark \\ 0.25(80)+0.50(120) &= &200\checkmark \\ {} &{} &\text{Yes!} \end{array} $
Step 7. Answer the question.	Sasheena should mix $80 \space ml$ of the $25\%$ solution with $120 \space ml$ of the $50\%$ solution to get the $200\space ml$ of a $40\%$ solution.

$try-it.png$ $\PageIndex{14}$

Translate to a system of equations and solve:

LeBron needs 150 milliliters of a 30% solution of sulfuric acid for a lab experiment but only has access to a 25% and a 50% solution. How much of the 25% and how much of the 50% solution should he mix to make the 30% solution?

Answer: 120 ml of 25% solution and 30 ml of 50% solution

Solve Interest Applications

The formula to model simple interest applications is $I=Prt$. Interest, I, is the product of the principal, P, the rate, r, and the time, t. In our work here, we will calculate the interest earned in one year, so t will be 1.

We modify the column titles in the mixture table to show the formula for interest, as you’ll see in the next example.

Example $\PageIndex{15}$

Translate to a system of equations and solve:

Adnan has $40,000 to invest and hopes to earn $7.1\%$ interest per year. He will put some of the money into a stock fund that earns 8% per year and the rest into bonds that earn 3% per year. How much money should he put into each fund?

Solution

Step 1. Read the problem.	A chart will help us organize the information.
Step 2. Identify what we are looking for.	We are looking for the amount to invest in each fund.
Step 3. Name what we are looking for.	Let $s= \text{the amount invested in stocks,}$ $b= \text{the amount invested in bonds.}$
Write the interest rate as a decimal for each fund. Multiply: Principal · Rate · Time	$.$
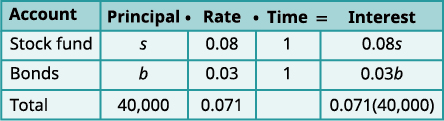Step 4. Translate into a system of equations. We get our system of equations from the Principal column and the Interest column.	$.$
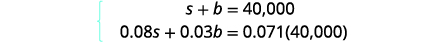Step 5. Solve the system of equations by elimination. Multiply the top equation by $−0.03$.	$.$
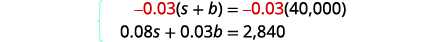Simplify and add to solve for s.	$.$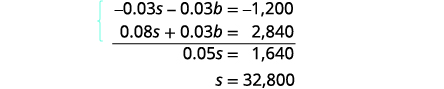
To find b, substitute s = 32,800 into the first equation.	$.$
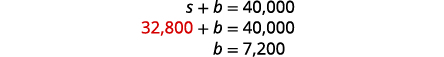Step 6. Check the answer in the problem.	We leave the check to you.
Step 7. Answer the question.	Adnan should invest $32,800 in stock and $7,200 in bonds.

Did you notice that the Principal column represents the total amount of money invested while the Interest column represents only the interest earned? Likewise, the first equation in our system, $s+b=40,000$, represents the total amount of money invested and the second equation, $0.08s+0.03b=0.071(40,000)$, represents the interest earned.

$try-it.png$ $\PageIndex{15A}$

Translate to a system of equations and solve:

Leon had $50,000 to invest and hopes to earn $6.2%$ interest per year. He will put some of the money into a stock fund that earns 7% per year and the rest in to a savings account that earns 2% per year. How much money should he put into each fund?

Answer: $42,000 in the stock fund and $8000 in the savings account

$try-it.png$ $\PageIndex{15B}$

Translate to a system of equations and solve:

Cherish invested $7000 into two stock investments. One stock paid 11% interest and the other stock paid 13% interest. She earned $12.5%$ interest on the total investment. How much money did she put in each stock?

Answer: $1750 at 11% and $5250 at 13%

The next example requires that we find the principal given the amount of interest earned.

Example $\PageIndex{16}$

Translate to a system of equations and solve:

Carlos owes $21,540 on his two student loans. The interest rate on his bank loan is $10.5%$ and the interest rate on the federal loan is $5.9%$. The total amount of interest he paid last year was $$1,669.68$. What was the principal for each loan?

Solution

Step 1. Read the problem.	A chart will help us organize the information.
Step 2. Identify what we are looking for.	We are looking for the principal of each loan.
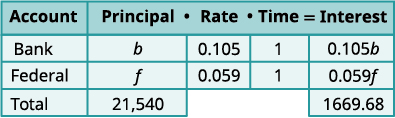
Step 3. Name what we are looking for.	Let $b= \text{the principal for the bank loan,}$ $f= \text{the principal on the federal loan.}$
The total loans are $21,540.
Record the interest rates as decimals in the chart. Multiply using the formula I = Prt to get the Interest.	$.$
Step 4. Translate into a system of equations. The system of equations comes from the Principal column and the Interest column.	$.$
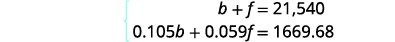Step 5. Solve the system of equations We will use substitution to solve. Solve the first equation for b.	$.$
	$.$
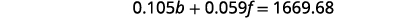Substitute b = −f + 21.540 into the second equation.	$.$
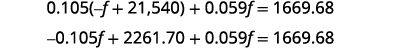Simplify and solve for f.	$.$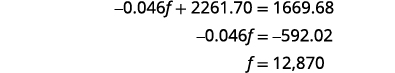
To find b, substitute f = 12,870 into the first equation.	$.$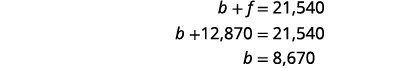
Step 6. Check the answer in the problem.	We leave the check to you.
Step 7. Answer the question.	The principal of the federal loan was $12,870 and the principal for the bank loan was $8,670.

$try-it.png$ $\PageIndex{16A}$

Translate to a system of equations and solve:

Hong owes $18,000 on her student loans. The interest rate on the bank loan is 2.5% and the interest rate on the federal loan is 6.9%. The total amount of interest she paid last year was $1,066. What was the principal for each loan?

Answer: Bank $4,000; Federal $14,000

$try-it.png$ $\PageIndex{16B}$

Translate to a system of equations and solve:

Jill’s Sandwich Shoppe owes $65,200 on two business loans, one at 4.5% interest and the other at 7.2% interest. The total amount of interest owed last year was $3,582. What was the principal for each loan?

Answer: $41,200 at 4.5%, $24,000 at 7.2%

Solve applications of cost and revenue functions

Suppose a company makes and sells x units of a product. The cost to the company is the total costs to produce x units. This is the cost to manufacture for each unit times x, the number of units manufactured, plus the fixed costs.

The revenue is the money the company brings in as a result of selling x units. This is the selling price of each unit times the number of units sold.

When the costs equal the revenue we say the business has reached the break-even point.

COST AND REVENUE FUNCTIONS

The cost function is the cost to manufacture each unit times x, the number of units manufactured, plus the fixed costs.

\[C(x)=(\text{cost per unit})·x+\text{fixed costs}\nonumber \]

The revenue function is the selling price of each unit times x, the number of units sold.

\[R(x)=(\text{selling price per unit})·x\nonumber \]

The break-even point is when the revenue equals the costs.

\[C(x)=R(x)\nonumber\]

Example $\PageIndex{17}$

The manufacturer of a weight training bench spends $105 to build each bench and sells them for $245. The manufacturer also has fixed costs each month of $7,000.

a. Find the cost function C when x benches are manufactured.

b. Find the revenue function R when x benches are sold.

c. Show the break-even point by graphing both the Revenue and Cost functions on the same grid.

d. Find the break-even point. Interpret what the break-even point means.

Solution

a. The manufacturer has $7,000 of fixed costs no matter how many weight training benches it produces. In addition to the fixed costs, the manufacturer also spends $105 to produce each bench. Suppose x benches are sold.

$\begin{array} {ll} {\text{Write the general Cost function formula.}} &{C(x)=(\text{cost per unit})·x+\text{fixed costs}} \\ {\text{Substitute in the cost values.}} &{C(x)=105x+7000} \\ \end{array}$

b. The manufacturer sells each weight training bench for $245. We get the total revenue by multiplying the revenue per unit times the number of units sold.

$\begin{array} {ll} {\text{Write the general Revenue function.}} &{C(x)=(\text{selling price per unit})·x} \\ {\text{Substitute in the revenue per unit.}} &{R(x)=245x} \\ \end{array}$

c. Essentially we have a system of linear equations. We will show the graph of the system as this helps make the idea of a break-even point more visual.

\[\left\{ \begin{array} {l} C(x)=105x+7000 \\ R(x)=245x \end{array} \right. \quad \text{or} \quad \left\{ \begin{array} {l} y=105x+7000 \\ y=245x \end{array} \right. \nonumber \]

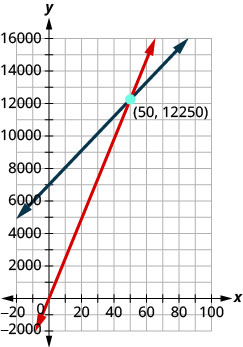
$Figure shows a graph with two intersecting lines. One of them passes through the origin.$

d. To find the actual value, we remember the break-even point occurs when costs equal revenue.

$\begin{array} {ll} {\text{Write the break-even formula.}} &{\begin{array} {l} {C(x)=R(x)} \\ {105x+7000=245x} \end{array}} \\ {\text{Solve.}} &{\begin{array} {l} {7000=140x} \\ {50=x} \end{array}} \\ \end{array}$

When 50 benches are sold, the costs equal the revenue.

$C of x is 105x plus 7000. C of 50 is 105 times 50 plus 7000, which is equal to 12250. R of x is 245x. R of 50 is 245 times 50, which is 12250.$

When 50 benches are sold, the revenue and costs are both $12,250. Notice this corresponds to the ordered pair $(50,12250)$.

$try-it.png$ $\PageIndex{17}$

The manufacturer of a weight training bench spends $15 to build each bench and sells them for $32. The manufacturer also has fixed costs each month of $25,500.

a. Find the cost function C when x benches are manufactured.

b. Find the revenue function R when x benches are sold.

c. Show the break-even point by graphing both the Revenue and Cost functions on the same grid.

d. Find the break-even point. Interpret what the break-even point means.

Answer

a. $C(x)=15x+25,500$

b. $R(x)=32x$

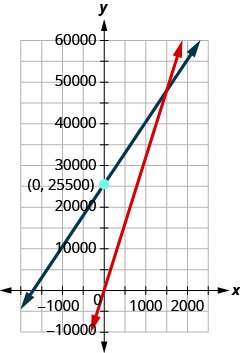
$Figure shows a graph with two intersecting lines. One of them passes through the origin. The other crosses the y axis at point 25,687.$

d. 1,5001,500; when 1,500 benches are sold, the cost and revenue will be both 48,000

Access this online resource for additional instruction and practice.

Key Concepts

How To Solve Applications with Systems of Equations
1. Read the problem. Make sure all the words and ideas are understood.
2. Identify what we are looking for.
3. Name what we are looking for. Choose variables to represent those quantities.
4. Translate into a system of equations.
5. Solve the system of equations using good algebra techniques.
6. Check the answer in the problem and make sure it makes sense.
7. Answer the question with a complete sentence.

Glossary

complementary angles: Two angles are complementary if the sum of the measures of their angles is 90 degrees.

supplementary angles: Two angles are supplementary if the sum of the measures of their angles is 180 degrees.
cost function: The cost function is the cost to manufacture each unit times xx, the number of units manufactured, plus the fixed costs; C(x) = (cost per unit)x + fixed costs.
revenue: The revenue is the selling price of each unit times x, the number of units sold; R(x) = (selling price per unit)x.
break-even point: The point at which the revenue equals the costs is the break-even point; C(x)=R(x).

Step 1. Read the problem. A figure may help us visualize the situation, then we will create a table to organize the information.	Sasheena must mix some of the \(25\%\) solution and some of the \(50\%\) solution together to get \(200\space ml\) of the \(40\%\) solution.
	$.$
Step 2. Identify what we are looking for.	We are looking for how much of each solution she needs.
Step 3. Name what we are looking for.	Let \(x= \text{number of ml of } 25\% \text{ solution,}\) \(y= \text{number of ml of }50\% \text{ solution.}\)
A table will help us organize the data. She will mix x \(ml\) of \(25%\) with y \(ml\) of \(50%\) to get \(200 \space ml\) of \(40%\) solution. We write the percents as decimals in the chart. We multiply the number of units times the concentration to get the total amount of sulfuric acid in each solution.	$.$
Step 4. Translate into a system of equations. We get the equations from the Number column and the Amount column. Now we have the system.	$.$
Step 5. Solve the system of equations We will solve the system by elimination. Multiply the first equation by \(−0.5\) to eliminate y.	$.$
Simplify and add to solve for x.	$.$
To solve for y, substitute \(x=80\) into the first equation.	$.$
Step 6. Check the answer in the problem. \(\begin{array} {lll} 80+120 &= &200\checkmark \\ 0.25(80)+0.50(120) &= &200\checkmark \\ {} &{} &\text{Yes!} \end{array} \)
Step 7. Answer the question.	Sasheena should mix \(80 \space ml\) of the \(25\%\) solution with \(120 \space ml\) of the \(50\%\) solution to get the \(200\space ml\) of a \(40\%\) solution.