3A.5E: Exercises

Last updated
Save as PDF

Page ID: 33590

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Practice Makes Perfect

Direct Translation Applications

In the following exercises, translate to a system of equations and solve.

1. The sum of two number is 15. One number is 3 less than the other. Find the numbers.

2. The sum of two number is 30. One number is 4 less than the other. Find the numbers.

Answer: 13 and 17

3. The sum of two number is −16. One number is 20 less than the other. Find the numbers.

4. The sum of two number is $−26$. One number is 12 less than the other. Find the numbers.

Answer: $−7$ and $−19$

5. The sum of two numbers is 65. Their difference is 25. Find the numbers.

6. The sum of two numbers is 37. Their difference is 9. Find the numbers.

Answer: $14$ and $23$

7. The sum of two numbers is $−27$. Their difference is $−59$. Find the numbers.

8. The sum of two numbers is $−45$. Their difference is $−89$. Find the numbers.

Answer: $22$ and $−67$

9. Maxim has been offered positions by two car companies. The first company pays a salary of $10,000 plus a commission of $1000 for each car sold. The second pays a salary of $20,000 plus a commission of $500 for each car sold. How many cars would need to be sold to make the total pay the same?

10. Jackie has been offered positions by two cable companies. The first company pays a salary of $14,000 plus a commission of $100 for each cable package sold. The second pays a salary of $20,000 plus a commission of $25 for each cable package sold. How many cable packages would need to be sold to make the total pay the same?

Answer: Eighty cable packages would need to be sold to make the total pay the same.

11. Amara currently sells televisions for company A at a salary of $17,000 plus a $100 commission for each television she sells. Company B offers her a position with a salary of $29,000 plus a $20 commission for each television she sells. How televisions would Amara need to sell for the options to be equal?

12. Mitchell currently sells stoves for company A at a salary of $12,000 plus a $150 commission for each stove he sells. Company B offers him a position with a salary of $24,000 plus a $50 commission for each stove he sells. How many stoves would Mitchell need to sell for the options to be equal?

Answer: Mitchell would need to sell 120 stoves for the companies to be equal.

13. Two containers of gasoline hold a total of fifty gallons. The big container can hold ten gallons less than twice the small container. How many gallons does each container hold?

14. June needs 48 gallons of punch for a party and has two different coolers to carry it in. The bigger cooler is five times as large as the smaller cooler. How many gallons can each cooler hold?

Answer: 8 and 40 gallons

15. Shelly spent 10 minutes jogging and 20 minutes cycling and burned 300 calories. The next day, Shelly swapped times, doing 20 minutes of jogging and 10 minutes of cycling and burned the same number of calories. How many calories were burned for each minute of jogging and how many for each minute of cycling?

16. Drew burned 1800 calories Friday playing one hour of basketball and canoeing for two hours. Saturday he spent two hours playing basketball and three hours canoeing and burned 3200 calories. How many calories did he burn per hour when playing basketball? How many calories did he burn per hour when canoeing?

Answer: 1000 calories playing basketball and 400 calories canoeing

17. Troy and Lisa were shopping for school supplies. Each purchased different quantities of the same notebook and thumb drive. Troy bought four notebooks and five thumb drives for $116. Lisa bought two notebooks and three thumb dives for $68. Find the cost of each notebook and each thumb drive.

18. Nancy bought seven pounds of oranges and three pounds of bananas for $17. Her husband later bought three pounds of oranges and six pounds of bananas for $12. What was the cost per pound of the oranges and the bananas?

Answer: Oranges cost $2 per pound and bananas cost $1 per pound

19. Andrea is buying some new shirts and sweaters. She is able to buy 3 shirts and 2 sweaters for $114 or she is able to buy 2 shirts and 4 sweaters for $164. How much does a shirt cost? How much does a sweater cost?

20. Peter is buying office supplies. He is able to buy 3 packages of paper and 4 staplers for $40 or he is able to buy 5 packages of paper and 6 staplers for $62. How much does a package of paper cost? How much does a stapler cost?

Answer: Package of paper $4, stapler $7

21. The total amount of sodium in 2 hot dogs and 3 cups of cottage cheese is 4720 mg. The total amount of sodium in 5 hot dogs and 2 cups of cottage cheese is 6300 mg. How much sodium is in a hot dog? How much sodium is in a cup of cottage cheese?

22. The total number of calories in 2 hot dogs and 3 cups of cottage cheese is 960 calories. The total number of calories in 5 hot dogs and 2 cups of cottage cheese is 1190 calories. How many calories are in a hot dog? How many calories are in a cup of cottage cheese?

Answer: Hot dog 150 calories, cup of cottage cheese 220 calories

23. Molly is making strawberry infused water. For each ounce of strawberry juice, she uses three times as many ounces of water as juice. How many ounces of strawberry juice and how many ounces of water does she need to make 64 ounces of strawberry infused water?

24. Owen is making lemonade from concentrate. The number of quarts of water he needs is 4 times the number of quarts of concentrate. How many quarts of water and how many quarts of concentrate does Owen need to make 100 quarts of lemonade?

Answer: Owen will need 80 quarts of water and 20 quarts of concentrate to make 100 quarts of lemonade.

Solve Geometry Applications

In the following exercises, translate to a system of equations and solve.

25. The difference of two complementary angles is 55 degrees. Find the measures of the angles.

26. The difference of two complementary angles is 17 degrees. Find the measures of the angles.

Answer: $53.5$ degrees and $36.5$ degree.

27. Two angles are complementary. The measure of the larger angle is twelve less than twice the measure of the smaller angle. Find the measures of both angles.

28. Two angles are complementary. The measure of the larger angle is ten more than four times the measure of the smaller angle. Find the measures of both angles.

Answer: 16 degrees and 74 degrees

29. The difference of two supplementary angles is 8 degrees. Find the measures of the angles.

30. The difference of two supplementary angles is 88 degrees. Find the measures of the angles.

Answer: 134 degrees and 46 degrees

31. Two angles are supplementary. The measure of the larger angle is four more than three times the measure of the smaller angle. Find the measures of both angles.

32. Two angles are supplementary. The measure of the larger angle is five less than four times the measure of the smaller angle. Find the measures of both angles.

Answer: 37 degrees and 143 degrees

33. The measure of one of the small angles of a right triangle is 14 more than 3 times the measure of the other small angle. Find the measure of both angles.

34. The measure of one of the small angles of a right triangle is 26 more than 3 times the measure of the other small angle. Find the measure of both angles.

Answer: $16°$ and $74°$

35. The measure of one of the small angles of a right triangle is 15 less than twice the measure of the other small angle. Find the measure of both angles.

36. The measure of one of the small angles of a right triangle is 45 less than twice the measure of the other small angle. Find the measure of both angles.

Answer: $45°$ and $45°$

37. Wayne is hanging a string of lights 45 feet long around the three sides of his patio, which is adjacent to his house. The length of his patio, the side along the house, is five feet longer than twice its width. Find the length and width of the patio.

38. Darrin is hanging 200 feet of Christmas garland on the three sides of fencing that enclose his front yard. The length is five feet less than three times the width. Find the length and width of the fencing.

Answer: Width is 41 feet and length is 118 feet.

39. A frame around a family portrait has a perimeter of 90 inches. The length is fifteen less than twice the width. Find the length and width of the frame.

40. The perimeter of a toddler play area is 100 feet. The length is ten more than three times the width. Find the length and width of the play area.

Answer: Width is 10 feet and length is 40 feet.

Solve Uniform Motion Applications

In the following exercises, translate to a system of equations and solve.

41. Sarah left Minneapolis heading east on the interstate at a speed of 60 mph. Her sister followed her on the same route, leaving two hours later and driving at a rate of 70 mph. How long will it take for Sarah’s sister to catch up to Sarah?

42. College roommates John and David were driving home to the same town for the holidays. John drove 55 mph, and David, who left an hour later, drove 60 mph. How long will it take for David to catch up to John?

Answer: 11 hours

43. At the end of spring break, Lucy left the beach and drove back towards home, driving at a rate of 40 mph. Lucy’s friend left the beach for home 30 minutes (half an hour) later, and drove 50 mph. How long did it take Lucy’s friend to catch up to Lucy?

44. Felecia left her home to visit her daughter driving 45 mph. Her husband waited for the dog sitter to arrive and left home twenty minutes (1/3 hour) later. He drove 55 mph to catch up to Felecia. How long before he reaches her?

Answer: $1.5$ hour

45. The Jones family took a 12-mile canoe ride down the Indian River in two hours. After lunch, the return trip back up the river took three hours. Find the rate of the canoe in still water and the rate of the current.

46. A motor boat travels 60 miles down a river in three hours but takes five hours to return upstream. Find the rate of the boat in still water and the rate of the current.

Answer: Boat rate is 16 mph and current rate is 4 mph.

47. A motor boat traveled 18 miles down a river in two hours but going back upstream, it took 4.54.5 hours due to the current. Find the rate of the motor boat in still water and the rate of the current. (Round to the nearest hundredth.)

48. A river cruise boat sailed 80 miles down the Mississippi River for four hours. It took five hours to return. Find the rate of the cruise boat in still water and the rate of the current.

Answer: Boat rate is 18 mph and current rate is 2 mph.

49. A small jet can fly 1072 miles in 4 hours with a tailwind but only 848 miles in 4 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

50. A small jet can fly 1435 miles in 5 hours with a tailwind but only 1,215 miles in 5 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Answer: Jet rate is 265 mph and wind speed is 22 mph.

51. A commercial jet can fly 868 miles in 2 hours with a tailwind but only 792 miles in 2 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

52. A commercial jet can fly 1,320 miles in 3 hours with a tailwind but only 1170 miles in 3 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Answer: Jet rate is 415 mph and wind speed is 25 mph.

Writing Exercises

53. Write an application problem similar to Example. Then translate to a system of equations and solve it.\

54. Write a uniform motion problem similar to Example that relates to where you live with your friends or family members. Then translate to a system of equations and solve it.

Answer: Answers will vary.

Practice Makes Perfect

Solve Mixture Applications

In the following exercises, translate to a system of equations and solve.

1. Tickets to a Broadway show cost $35 for adults and $15 for children. The total receipts for 1650 tickets at one performance were $47,150. How many adult and how many child tickets were sold?

2. Tickets for the Cirque du Soleil show are $70 for adults and $50 for children. One evening performance had a total of 300 tickets sold and the receipts totaled $17,200. How many adult and how many child tickets were sold?

Answer: 110 adult tickets, 190 child tickets

3. Tickets for an Amtrak train cost $10 for children and $22 for adults. Josie paid $1200 for a total of 72 tickets. How many children tickets and how many adult tickets did Josie buy?

4. Tickets for a Minnesota Twins baseball game are $69 for Main Level seats and $39 for Terrace Level seats. A group of sixteen friends went to the game and spent a total of $804 for the tickets. How many of Main Level and how many Terrace Level tickets did they buy?

Answer: 6 good seats, 10 cheap seats

5. Tickets for a dance recital cost $15 for adults and $7 dollars for children. The dance company sold 253 tickets and the total receipts were $2771. How many adult tickets and how many child tickets were sold?

6. Tickets for the community fair cost $12 for adults and $5 dollars for children. On the first day of the fair, 312 tickets were sold for a total of $2204. How many adult tickets and how many child tickets were sold?

Answer: 92 adult tickets, 220 children tickets

7. Brandon has a cup of quarters and dimes with a total value of $$3.80$. The number of quarters is four less than twice the number of quarters. How many quarters and how many dimes does Brandon have?

8. Sherri saves nickels and dimes in a coin purse for her daughter. The total value of the coins in the purse is $$0.95$. The number of nickels is two less than five times the number of dimes. How many nickels and how many dimes are in the coin purse?

Answer: 13 nickels, 3 dimes

9. Peter has been saving his loose change for several days. When he counted his quarters and nickels, he found they had a total value $$13.10$. The number of quarters was fifteen more than three times the number of dimes. How many quarters and how many dimes did Peter have?

10. Lucinda had a pocketful of dimes and quarters with a value of $$6.20$. The number of dimes is eighteen more than three times the number of quarters. How many dimes and how many quarters does Lucinda have?

Answer: 42 dimes, 8 quarters

11. A cashier has 30 bills, all of which are $10 or $20 bills. The total value of the money is $460. How many of each type of bill does the cashier have?

12. A cashier has 54 bills, all of which are $10 or $20 bills. The total value of the money is $910. How many of each type of bill does the cashier have?

Answer: 17 $10 bills, 37 $20 bills

13. Marissa wants to blend candy selling for $$1.80$ per pound with candy costing $$1.20$ per pound to get a mixture that costs her $$1.40$ per pound to make. She wants to make 90 pounds of the candy blend. How many pounds of each type of candy should she use?

14. How many pounds of nuts selling for $6 per pound and raisins selling for $3 per pound should Kurt combine to obtain 120 pounds of trail mix that cost him $5 per pound?

Answer: 80 pounds nuts and 40 pounds raisins

15. Hannah has to make twenty-five gallons of punch for a potluck. The punch is made of soda and fruit drink. The cost of the soda is $$1.79$ per gallon and the cost of the fruit drink is $$2.49$ per gallon. Hannah’s budget requires that the punch cost $$2.21$ per gallon. How many gallons of soda and how many gallons of fruit drink does she need?

16. Joseph would like to make twelve pounds of a coffee blend at a cost of $6 per pound. He blends Ground Chicory at $5 a pound with Jamaican Blue Mountain at $9 per pound. How much of each type of coffee should he use?

Answer: 9 pounds of Chicory coffee, 3 pounds of Jamaican Blue Mountain coffee

17. Julia and her husband own a coffee shop. They experimented with mixing a City Roast Columbian coffee that cost $7.80 per pound with French Roast Columbian coffee that cost $8.10 per pound to make a twenty-pound blend. Their blend should cost them $7.92 per pound. How much of each type of coffee should they buy?

18. Twelve-year old Melody wants to sell bags of mixed candy at her lemonade stand. She will mix M&M’s that cost $4.89 per bag and Reese’s Pieces that cost $3.79 per bag to get a total of twenty-five bags of mixed candy. Melody wants the bags of mixed candy to cost her $4.23 a bag to make. How many bags of M&M’s and how many bags of Reese’s Pieces should she use?

Answer: 10 bags of M&M’s, 15 bags of Reese’s Pieces

19. Jotham needs 70 liters of a 50% solution of an alcohol solution. He has a 30% and an 80% solution available. How many liters of the 30% and how many liters of the 80% solutions should he mix to make the 50% solution?

20. Joy is preparing 15 liters of a 25% saline solution. She only has 40% and 10% solution in her lab. How many liters of the 40% and how many liters of the 10% should she mix to make the 25% solution?

Answer: $7.5$ liters of each solution

21. A scientist needs 65 liters of a 15% alcohol solution. She has available a 25% and a 12% solution. How many liters of the 25% and how many liters of the 12% solutions should she mix to make the 15% solution?

22. A scientist needs 120 milliliters of a 20% acid solution for an experiment. The lab has available a 25% and a 10% solution. How many liters of the 25% and how many liters of the 10% solutions should the scientist mix to make the 20% solution?

Answer: 80 liters of the 25% solution and 40 liters of the 10% solution

23. A 40% antifreeze solution is to be mixed with a 70% antifreeze solution to get 240 liters of a 50% solution. How many liters of the 40% and how many liters of the 70% solutions will be used?

24. A 90% antifreeze solution is to be mixed with a 75% antifreeze solution to get 360 liters of an 85% solution. How many liters of the 90% and how many liters of the 75% solutions will be used?

Answer: 240 liters of the 90% solution and 120 liters of the 75% solution

Solve Interest Applications

In the following exercises, translate to a system of equations and solve.

25. Hattie had $3000 to invest and wants to earn 10.6%10.6% interest per year. She will put some of the money into an account that earns 12% per year and the rest into an account that earns 10% per year. How much money should she put into each account?

26. Carol invested $2560 into two accounts. One account paid 8% interest and the other paid 6% interest. She earned 7.25%7.25% interest on the total investment. How much money did she put in each account?

Answer: $1600 at 8%, 960 at 6%

27. Sam invested $48,000, some at 6% interest and the rest at 10%. How much did he invest at each rate if he received $4000 in interest in one year?

28. Arnold invested $64,000, some at $5.5%$ interest and the rest at 9%. How much did he invest at each rate if he received $4500 in interest in one year?

Answer: $28,000 at 9%, $36,000 at $5.5%$

29. After four years in college, Josie owes $65, 800 in student loans. The interest rate on the federal loans is $4.5%$ and the rate on the private bank loans is 2%. The total interest she owes for one year was $$2878.50$. What is the amount of each loan?

30. Mark wants to invest $10,000 to pay for his daughter’s wedding next year. He will invest some of the money in a short term CD that pays 12% interest and the rest in a money market savings account that pays 5% interest. How much should he invest at each rate if he wants to earn $1095 in interest in one year?

Answer: $8500 CD, $1500 savings account

31. A trust fund worth $25,000 is invested in two different portfolios. This year, one portfolio is expected to earn $5.25%$ interest and the other is expected to earn 4%. Plans are for the total interest on the fund to be $1150 in one year. How much money should be invested at each rate?

32. A business has two loans totaling $85,000. One loan has a rate of 6% and the other has a rate of 4.5% This year, the business expects to pay $4,650 in interest on the two loans. How much is each loan?

Answer: $55,000 on loan at 6% and $30,000 on loan at $4.5%$

Solve Applications of Cost and Revenue Functions

33. The manufacturer of an energy drink spends $1.20 to make each drink and sells them for $2. The manufacturer also has fixed costs each month of $8,000.

ⓐ Find the cost function C when x energy drinks are manufactured.

ⓑ Find the revenue function R when x drinks are sold.

ⓓ Find the break-even point. Interpret what the break-even point means.

34. The manufacturer of a water bottle spends $5 to build each bottle and sells them for $10. The manufacturer also has fixed costs each month of $6500. ⓐ Find the cost function C when x bottles are manufactured. ⓑ Find the revenue function R when x bottles are sold. ⓒ Show the break-even point by graphing both the Revenue and Cost functions on the same grid. ⓓ Find the break-even point. Interpret what the break-even point means.

Answer

ⓐ $C(x)=5x+6500$

ⓑ $R(x)=10x$

ⓒ

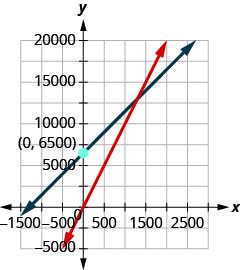
$Figure shows a graph with two intersecting lines. One of them passes through the origin. The other crosses the y axis at point 6560.$

ⓓ 1,500; when 1,500 water bottles are sold, the cost and the revenue equal $15,000

Writing Exercises

35. Take a handful of two types of coins, and write a problem similar to Example relating the total number of coins and their total value. Set up a system of equations to describe your situation and then solve it.

36. In Example, we used elimination to solve the system of equations
$\left\{ \begin{array} {l} s+b=40,000 \\ 0.08s+0.03b=0.071(40,000). \end{array} \right. $

Could you have used substitution or elimination to solve this system? Why?

Answer: Answers will vary.