Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

11.3: Two Population Means with Known Standard Deviations

Last updated

Apr 2, 2022
Save as PDF
- 11.2: Two Population Means with Unknown Standard Deviations
- 11.4: Comparing Two Independent Population Proportions

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Even though this situation is not likely (knowing the population standard deviations is not likely), the following example illustrates hypothesis testing for independent means, known population standard deviations. The sampling distribution for the difference between the means is normal and both populations must be normal. The random variable is $\bar{X}_{1} - \bar{X}_{2}$ . The normal distribution has the following format:

Normal distribution is:

$\bar{X}_{1} - \bar{X}_{2} \sim{N}\left[\mu_{1} - \mu_{2}, \sqrt{\dfrac{(\sigma_{1})^{2}}{n_{1}} + \dfrac{(\sigma_{2})^{2}}{n_{2}}}\right] \label{eq1}$

The standard deviation is:

$\sqrt{\dfrac{(\sigma_{1})^{2}}{n_{1}} + \dfrac{(\sigma_{2})^{2}}{n_{2}}}\label{eq2}$

The test statistic (z-score) is:

$z = \dfrac{(\bar{x}_{1} - \bar{x}_{2}) - (\mu_{1} - \mu_{2})}{\sqrt{\dfrac{(\sigma_{1})^{2}}{n_{1}} + \dfrac{(\sigma_{2})^{2}}{n_{2}}}} \label{eq3}$

Example $\PageIndex{1}$

Independent groups, population standard deviations known: The mean lasting time of two competing floor waxes is to be compared. Twenty floors are randomly assigned to test each wax. Both populations have a normal distributions. The data are recorded in Table.

Wax	Sample Mean Number of Months Floor Wax Lasts	Population Standard Deviation
1	3	0.33
2	2.9	0.36

Does the data indicate that wax 1 is more effective than wax 2? Test at a 5% level of significance.

Answer

This is a test of two independent groups, two population means, population standard deviations known.

Random Variable: $\bar{X}_{1} - \bar{X}_{2} =$ difference in the mean number of months the competing floor waxes last.

$H_{0}: \mu_{1} \leq \mu_{2}$
$H_{a}: \mu_{1} > \mu_{2}$

The words "is more effective" says that wax 1 lasts longer than wax 2, on average. "Longer" is a “>” symbol and goes into $H_{a}$ . Therefore, this is a right-tailed test.

Distribution for the test: The population standard deviations are known so the distribution is normal. Using Equation $\ref{eq1}$ , the distribution is:

$\bar{X}_{1} - \bar{X}_{2} \sim{N} \left(0, \sqrt{\dfrac{0.33^{2}}{20} + \dfrac{0.36^{2}}{20}}\right)$

Since $\mu_{1} \leq \mu_{2}$ then $\mu_{1} - \mu_{2} \leq 0$ and the mean for the normal distribution is zero.

Calculate the $p\text{-value}$ using the normal distribution: $p\text{-value} = 0.1799$

Graph:

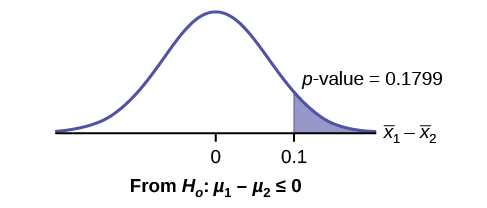This is a normal distribution curve with mean equal to zero. The values 0 and 0.1 are labeled on the horiztonal axis. A vertical line extends from 0.1 to the curve. The region under the curve to the right of the line is shaded to represent p-value = 0.1799.

Figure 10.3.1.

$\bar{X}_{1} - \bar{X}_{2} = 3 – 2.9 = 0.1$

Compare $\alpha$ and the $p\text{-value}$ : $\alpha = 0.05$ and $p\text{-value} = 0.1799$ . Therefore, $\alpha < p\text{-value}$ .

Make a decision: Since $\alpha < p\text{-value}$ , do not reject $H_{0}$ .

Conclusion: At the 5% level of significance, from the sample data, there is not sufficient evidence to conclude that the mean time wax 1 lasts is longer (wax 1 is more effective) than the mean time wax 2 lasts.

The Two Independent Samples With Statistics and Known Population Standard Deviations calculator is much more direct. Just enter in:

First Sample Sample Size = 20, First Sample Sample Size = 3, First Sample Population Standard Deviation = 0.33

Second Sample Sample Size = 20, Second Sample Sample Size = 2.9, Second Sample Population Standard Deviation = 0.36

Check ">" and click on Calculate. The $p\text{-value}$ is $p = 0.1799$ and the test statistic is 0.9157.

Two Independent Samples with statistics, Population Standard Deviation known Calculator

Enter in the statistics, the tail type and the confidence level and hit Calculate and the test statistic, t, the p-value, p, the confidence interval's lower bound, LB, and the upper bound, UB will be shown. Be sure to enter the confidence level as a decimal, e.g., 95% has a CL of 0.95.

	Sample Size	Sample Mean	Population Standard Deviation
First Sample
Second Sample

$\lt$

$\gt$

$\neq$

CL:

LB:

UB:

Exercise $\PageIndex{1}$

The means of the number of revolutions per minute of two competing engines are to be compared. Thirty engines are randomly assigned to be tested. Both populations have normal distributions. Table shows the result. Do the data indicate that Engine 2 has higher RPM than Engine 1? Test at a 5% level of significance.

Engine	Sample Mean Number of RPM	Population Standard Deviation
1	1,500	50
2	1,600	60

Answer

The $p\text{-value}$ is almost 0, so we reject the null hypothesis. There is sufficient evidence to conclude that Engine 2 runs at a higher RPM than Engine 1.

Example $\PageIndex{2}$ : Age of Senators

An interested citizen wanted to know if Democratic U. S. senators are older than Republican U.S. senators, on average. On May 26 2013, the mean age of 30 randomly selected Republican Senators was 61 years 247 days old (61.675 years) with a standard deviation of 10.17 years. The mean age of 30 randomly selected Democratic senators was 61 years 257 days old (61.704 years) with a standard deviation of 9.55 years.

Do the data indicate that Democratic senators are older than Republican senators, on average? Test at a 5% level of significance.

Answer

This is a test of two independent groups, two population means. The population standard deviations are unknown, but the sum of the sample sizes is 30 + 30 = 60, which is greater than 30, so we can use the normal approximation to the Student’s-t distribution. Subscripts: 1: Democratic senators 2: Republican senators

Random variable: $\bar{X}_{1} - \bar{X}_{2} =$ difference in the mean age of Democratic and Republican U.S. senators.

$H_{0}: \mu_{1} \leq \mu_{2} H_{0}: \mu_{1} - \mu_{2} \leq 0$
$H_{a}: \mu_{1} > \mu_{2} H_{a}: \mu_{1} - \mu_{2} > 0$

The words "older than" translates as a “>” symbol and goes into $H_{a}$ . Therefore, this is a right-tailed test.

Distribution for the test: The distribution is the normal approximation to the Student’s t for means, independent groups. Using the formula, the distribution is: $\bar{X}_{1} - \bar{X}_{2} \sim N\left[0, \sqrt{\dfrac{(9.55)^{2}}{30} + \dfrac{(10.17)^{2}}{30}}\right]$

Since $\mu_{1} \leq \mu_{2}, \mu_{1} - \mu_{2} \leq 0$ and the mean for the normal distribution is zero.

(Calculating the p-value using the normal distribution gives $p\text{-value} = 0.4040$ )

Graph:

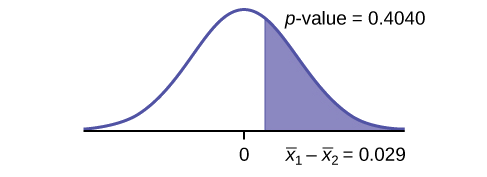This is a normal distribution curve with mean equal to zero. A vertical line to the right of zero extends from the axis to the curve. The region under the curve to the right of the line is shaded representing p-value = 0.4955.

Figure 10.3.2.

Compare $\alpha$ and the $p\text{-value}$ : $\alpha = 0.05$ and $p\text{-value} = 0.4040$ . Therefore, $\alpha < p\text{-value}$ .

Make a decision: Since $\alpha < p\text{-value}$ , do not reject $H_{0}$ .

Conclusion: At the 5% level of significance, from the sample data, there is not sufficient evidence to conclude that the mean age of Democratic senators is greater than the mean age of the Republican senators.

References

Data from the United States Census Bureau. Available online at http://www.census.gov/prod/cen2010/b...c2010br-02.pdf
Hinduja, Sameer. “Sexting Research and Gender Differences.” Cyberbulling Research Center, 2013. Available online at http://cyberbullying.us/blog/sexting...r-differences/ (accessed June 17, 2013).
“Smart Phone Users, By the Numbers.” Visually, 2013. Available online at http://visual.ly/smart-phone-users-numbers (accessed June 17, 2013).
Smith, Aaron. “35% of American adults own a Smartphone.” Pew Internet, 2013. Available online at http://www.pewinternet.org/~/media/F...martphones.pdf (accessed June 17, 2013).
“State-Specific Prevalence of Obesity AmongAduls—Unites States, 2007.” MMWR, CDC. Available online at http://www.cdc.gov/mmwr/preview/mmwrhtml/mm5728a1.htm (accessed June 17, 2013).
“Texas Crime Rates 1960–1012.” FBI, Uniform Crime Reports, 2013. Available online at: http://www.disastercenter.com/crime/txcrime.htm (accessed June 17, 2013).

Chapter Review

A hypothesis test of two population means from independent samples where the population standard deviations are known (typically approximated with the sample standard deviations), will have these characteristics:
Random variable: $\bar{X}_{1} - \bar{X}_{2} =$ the difference of the means
Distribution: normal distribution

Formula Review

Normal Distribution:

$\bar{X}_{1} - \bar{X}_{2} \sim N\left[\mu_{1} - \mu_{2}, \sqrt{\dfrac{(\sigma_{1})^{2}}{n_{1}} + \dfrac{(\sigma_{2})^{2}}{n_{2}}}\right]$

Generally $\mu_{1} - \mu_{2} = 0$ .

Test Statistic (z-score):

$z = \dfrac{(\bar{x}_{1} - \bar{x}_{2}) - (\mu_{1} - \mu_{2})}{\sqrt{\dfrac{(\sigma_{1})^{2}}{n_{1}} + \dfrac{(\sigma_{2})^{2}}{n_{2}}}}$

Generally $\mu_{1} - \mu_{2} = 0$ .

where:

$\sigma_{1}$ and $\sigma_{2}$ are the known population standard deviations. $n_{1}$ and $n_{1}$ are the sample sizes. $\bar{x}_{1}$ and $\bar{x}_{2}$ are the sample means. $\mu_{1}$ and $\mu_{2}$ are the population means

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/30189442-699...b91b9de@18.114.

References

Chapter Review

Formula Review

Contributors and Attributions

Support Center

How can we help?