5.3: Subtraction
- Page ID
- 132888
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Taking Away
How would you explain subtraction? How would you use manipulatives to explain how to do subtraction to a young child?
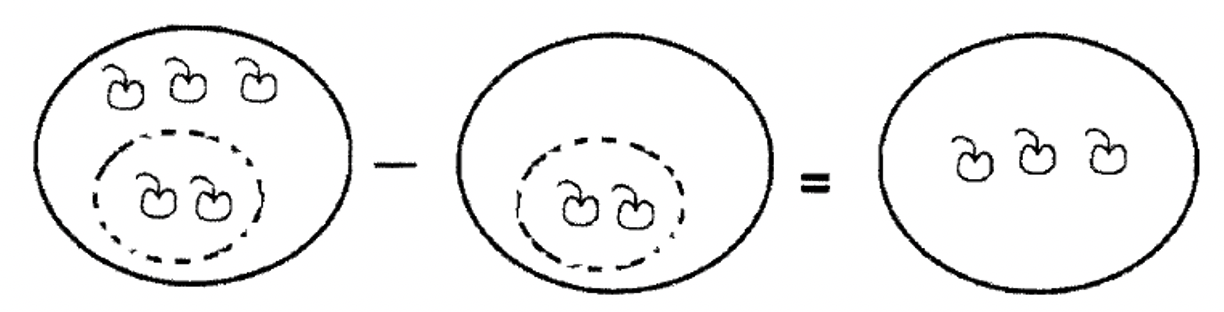
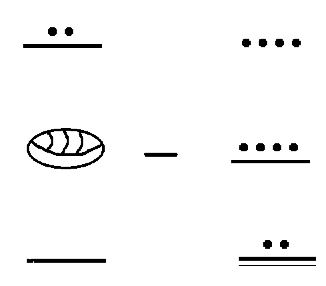
There are three major categories of situations that call for subtraction: taking away (or taking from), taking apart, and comparing. Most of us are default to thinking of subtraction as taking away. This is because it is associated with an easily acted out or imagined activity. A typical way someone might introduce the idea of subtraction is by saying "If I put five apples in the bowl and then take away two of the apples, how many are left in the bowl?" The illustration below shows this as a subtraction problem where after two apples are removed from the bowl, there are three apples remaining.
Let's use the action of taking away to subtract Maya numerals. It's similar to addition in that you remove a subset at each level – exchanges or trades might have to be done before being able to take away at any given level. Pay close attention to which level you are on when making exchanges. A dot at one level can be traded in for a group of 20 at the next level down except from level three to level two – one dot at the third level is replaced by a group of 18 at the second level. Study the following examples. See if you can figure out which exchanges are being made. I will indicate exchanges which are being made from one level to the other with a downward arrow.
Perform the subtraction below.
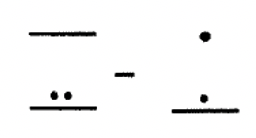
Solution
For this difference, in order to take one dot in the second level of subtrahend from the bar in the second level of the minuend, we must exchange the bar for five dots.

Let's try another example, but this time we will need to do the equivalent of what is often called "borrowing" in the standard American subtraction algorithm.
Perform the subtraction below.
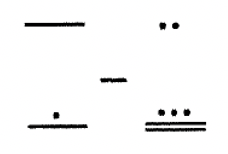
Solution
The bar in the second level of the minuend must be exchanged for five dots for two reasons. First, we need dots in order to take the two dots in the second level of the subtrahend away from it. Second, we need to exchange one of those second level dots for a 20 units (in the work below, this is written with four bars) in the first level.
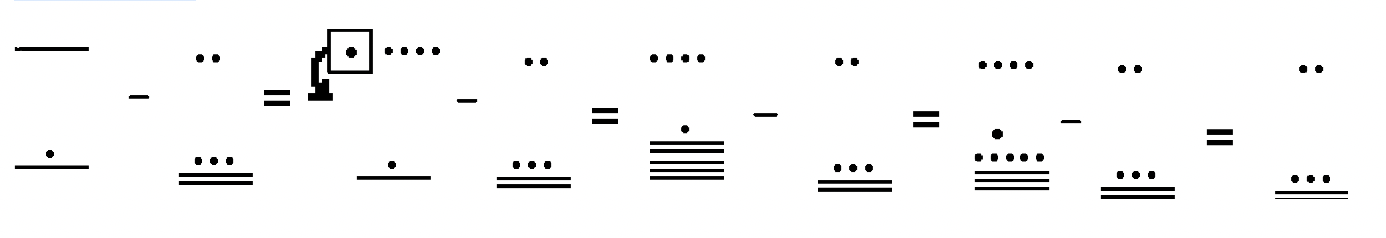
In the previous two examples, note that as exchanges are being made in the minuend (so that you can use the take-away approach), the subtrahend just keeps getting repeated. Alternately, you can first show the exchanges being made for the minuend, make a break (like a dotted line as shown below) and then write the subtraction problem out and subtract.
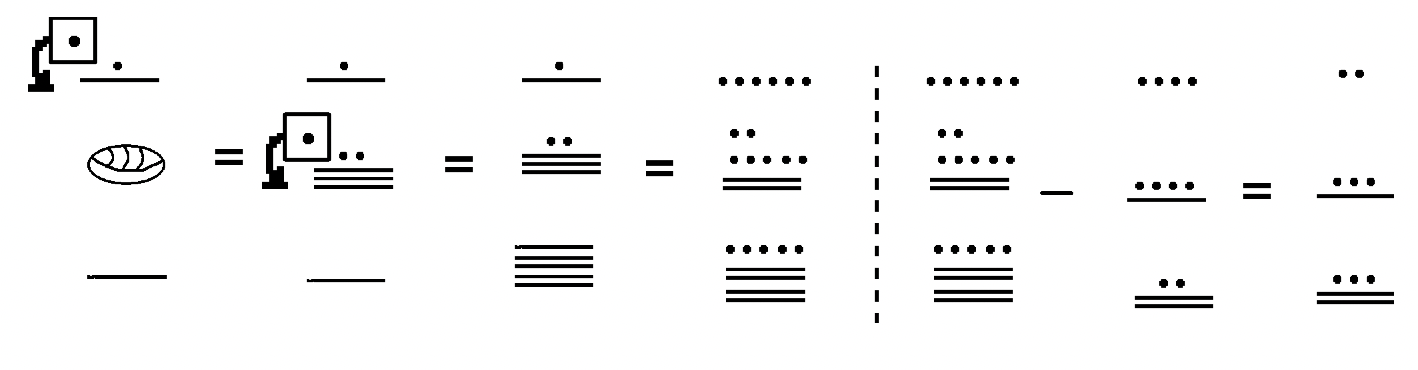
Perform the subtraction below. Note that the values here have three levels, so we must be careful when exchanging between the second and third levels.
Solution
In this example, we organize our work in the alternative way described above. We work just with the minuend first. Once we have enough dots and bars in each level of the minuend to take the dots in bars of each level of the subtrahend away, we proceed with the subtraction.
Let's try a difference of two values with four levels.
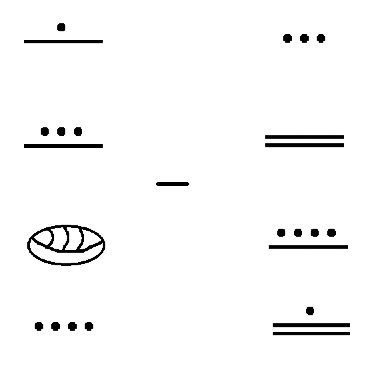
Solution
Once again, we must be careful to exchange one unit in the third level for 18 units in the second level.
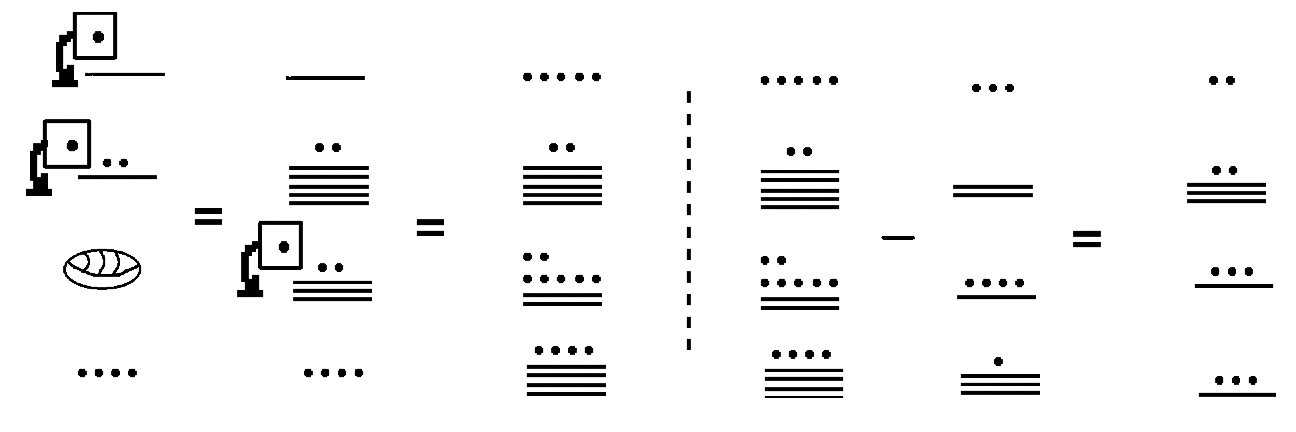
It takes a lot of concentration and effort to work these correctly. Perform each step carefully because it is easy to make mistakes. Each of the previous four examples can be checked by adding the answer to the subtrahend and seeing if the sum is the minuend. The other way to check is convert the minuend and subtrahend to Hindu-Arabic, subtract in Hindu-Arabic, then convert the difference to a Maya numeral. Try doing both forms of checking your answers. If one of them doesn't check out, see if you can find your error(s).
Perform the following subtraction problems using only Maya numerals. Show all steps and check!
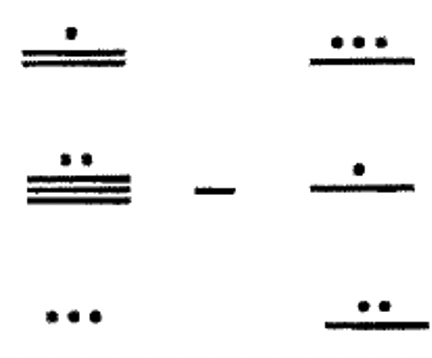
|
|
|
|
Children living in the U.S. these days will not be writing numbers in Maya, so we use manipulatives that reflect the Hindu-Arabic numeration system we use. To help you understand the difficulty a child just learning subtraction might have, we will work in base four. This means our manipulatives will be base four blocks.
Subtract \(101_\text{four}-13_\text{four}\) using base four blocks.
Solution
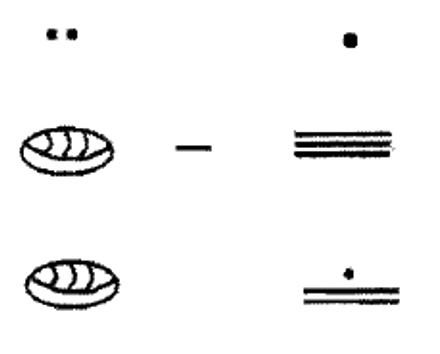
We will make a pile, called Pile A, using the base four blocks to represent \(101_\text{four}\) and another pile, called Pile B, to represent \(13_\text{four}\). Your piles should look something like what you see here.
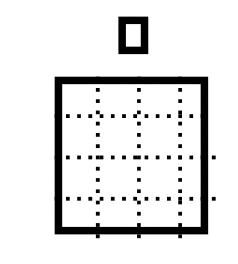
|
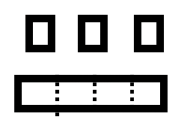
|
Below is an illustration of the subtraction problem being performed by taking away the blocks in the subtrahend from the box in the minuend. But to do this, a copy of Pile B must be a contained Pile A.
First, the flat in Pile A must be exchanged for four longs, and one of those longs must be exchanged for four units.There is a box around the subset (Pile B) to be removed from Pile A note how it matches Pile B. After taking those blocks away, 2 longs and 2 units remain. Therefore, the completed subtraction problem is \(101_{\text{four}} – 13_{\text{four}} = 22_{\text{four}}\).
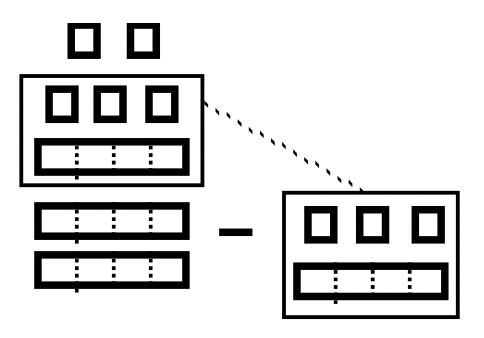 Pile A - Pile B Pile A - Pile B |
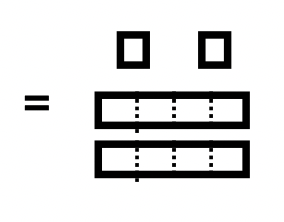 |
Let's check our answer using the numeration system we are more familiar with. We will write base ten numerals without the "ten" subscript to keep things less cluttered. First, we convert \(101_\text{four}\) to a Hindu-Arabic numeral.
\(101_\text{four} = 1\cdot 4^2 + 1\cdot 4^0 = 16+1 = 17\)
We do the same for \(13_\text{four}\).
\(13_\text{four} = 1\cdot 4^1 + 3\cdot 4^0 = 4+3 = 7\)
So, \(101_\text{four}-13_\text{four} = 17-7 = 10\). In the example, we got \(22_\text{four}\). So, we convert that too.
\(22_\text{four} = 2\cdot 4^1 + 2\cdot 4^0 = 8+2 = 10\)
It checks out!
Now it is your turn to do some "taking away" in another base.
Follow the directions below to subtract \( 17-9 \) in base five. In order for you to get practice converting to other bases, you must first convert 17 and 9 to base five.
Count out 17 unit blocks and make exchanges with base five blocks. Put them in a pile, called Pile A, and save this pile. Since you've made exchanges in base five, write 17 as a base five numeral on the space provided for Pile A below. Now, do the same for 9 to form Pile B and write 9 as a base five numeral on the space provided for Pile B below.
If necessary, make exchanges within Pile A so that an exact copy of Pile B is seen in Pile A. Take away those blocks in Pile A which represent the blocks in Pile B. The blocks left in Pile A are those that are left after subtracting the blocks that were in Pile B. If necessary, make any exchanges with base five blocks and then write this number as a base five numeral on the third blank provided below.
Below is the subtraction problem you have just performed in base five :
____________[Pile A] + _____________[Pile B] = _____________________[Difference of Pile A and B]
Convert the difference (answer) to base ten. It should be 8 since 17 – 9 = 8. Is it?
Let's try another one in a different base.
Follow the directions below to subtract \( 21-6 \) in base eight.
Count out 21 unit blocks and make exchanges with base eight blocks. Put them in a pile, called Pile A, and save this pile. Since you've made exchanges in base eight, write 21 as a base eight numeral on the space provided for Pile A below. Now, do the same for 6 to form Pile B and write 6 as a base eight numeral on the space provided for Pile B below.
If necessary, make exchanges within Pile A so that an exact copy of Pile B is seen in Pile A. Take away those blocks in Pile A which represent the blocks in Pile B. The blocks left in Pile A are those that are left after subtracting the blocks that were in Pile B. If necessary, make any exchanges with base eight blocks and then write this number as a base eight numeral on the third blank provided below.
Below is the subtraction problem you have just performed in base eight :
____________[Pile A] + _____________[Pile B] = _____________________[Difference of Pile A and B]
Convert the difference (answer) to base ten. It should be 15 since 21 – 6 = 15. Is it?
Let's do one more in a smaller base.
Follow the directions below to subtract \( 21-7 \) in base three.
Count out 21 unit blocks and make exchanges with base three blocks. Put them in a pile, called Pile A, and save this pile. Since you've made exchanges in base eight, write 21 as a base three numeral on the space provided for Pile A below. Now, do the same for 7 to form Pile B and write 7 as a base three numeral on the space provided for Pile B below.
If necessary, make exchanges within Pile A so that an exact copy of Pile B is seen in Pile A. Take away those blocks in Pile A which represent the blocks in Pile B. The blocks left in Pile A are those that are left after subtracting the blocks that were in Pile B. If necessary, make any exchanges with base three blocks and then write this number as a base eight numeral on the third blank provided below.
Below is the subtraction problem you have just performed in base three :
____________[Pile A] + _____________[Pile B] = _____________________[Difference of Pile A and B]
Convert the difference (answer) to base ten. It should be 14 since 21 – 7 = 14. Is it?
Write the three subtraction problems from the previous exercises in a vertical format like the one in base four shown. Study this base four problem as well as the three problems you write down. Try to figure out a way to do the subtraction problems using paper and pencil instead of by using the multibase blocks. In other words, try to come up with your own algorithm (method) for doing subtraction in other bases. Explain your method and show a few examples. Later, you will be learning algorithms for subtraction.
\[ \begin{aligned} 101_{\text{ four}} \\ \underline{ - 13_{\text{ four}}} \\ 22_{\text{ four}} \end{aligned} \nonumber \]
Think Deeper
Closure
It is important that you are able to think deeply about elementary school level mathematics. This is both because it will help you better understand it and because children will likely ask you some interesting questions in the future. Consider the next question.
Is there a natural number (positive integer) answer for every natural number subtraction problem? In other words, if you subtract a natural number from another natural number, will the difference also be a natural number? Try to answer this and explain your answer. If the answer is no, try to find a counterexample.
An equivalent way to ask that question is, "Is subtraction of natural numbers closed?" The word "closed" in this case means that you stay within that set of numbers. If you answered correctly, your answer was "no". To find a counterexample, we only need to choose a minuend and subtrahend such that the minuend is smaller than the subtrahend. For example, 5 – 7 = -2. Both 5 and 7 are natural numbers, but -2 is not. So, subtraction of natural numbers is not closed. What if we changed "natural numbers" to "integers". Think about this and once you have an answer, see if you can check your answer by talking with a classmate or searching the internet.
Missing Addends
If you think of subtraction in terms of missing addends, then we say that the statements \(a - b = c\) and \(a = b + c\) are equivalent to each other. Consider the statement, 8 – 2 = 6. It is equivalent to the statement 8 = 2 + 6. We also know that 2 + 6 = 6 + 2 because of what is called the commutative property of addition. Therefore, 8 = 6 + 2, which in turn is equivalent to the statement 8 – 6 = 2. This gives us four facts about how to relate the numbers 2, 6 and 8 using addition and subtraction
| 8 – 2 = 6 |
| 8 = 2 + 6 |
| 8 – 6 = 2 |
| 8 = 6 + 2 |
Some teachers relate subtraction and addition by using the idea of "fact families" such as the four facts above, which is one fact family.
Write down two subtraction statements that are equivalent to each addition statement.
| a. 9 + 5 = 14 | b. 2 + 21 = 23 |
We can use the equivalency of subtraction and addition equations to form a new approach for solving subtraction problems.
Subtract \(18-14\) using a missing addend approach.
Solution
Here, we will use a ? to indicate the value we are trying to find.
\(18-14 = ?\) is the same as \(14 + ? = 18\). Most adults quickly see that \(14+4 = 18\). But even if you were a child just learning addition, you could count on your fingers to find that fact. So, \(18-14 = 4\)
Try the next subtraction problems.
Perform the following subtraction problems by employing the missing addend approach. Fill in the blanks
| a. 9 – 7 = ____ because _____________ |
| b. 13 – 6 = ____ because _____________ |
| c. 88 – 8 = ____ because ______________ |
| d. 70 – 14 = ____ because _____________ |
As before, let's put ourselves in the position of children by trying to do the same thing in different bases.
Calculate \(143_{\text{six}} – 51_{\text{six}}\) using a missing addend approach.
Solution
First, \(143_{\text{six}} – 51_{\text{six}} = ?\) is equivalent to \(51_{\text{six}} + ? = 143_{\text{six}}\). Let's do this a little bit at a time.
\(51_{\text{six}} + 2_{\text{six}} = 53_{\text{six}}\)
We now have the digit we want to have in the ones place. Now we need to get a 4 in the sixes place. That's a little difficult to do, so let's first just try for getting 0. To do this, we note that in base six, since 5 + 1 = 6, \(5_{\text{six}} + 1_{\text{six}} = 10_{\text{six}}\). So, we can now get that 0.
\(53_{\text{six}} + 10_{\text{six}} = 103_{\text{six}}\)
Notice that we got the 1 in the thirty-sixes place already! So, we truly only need to get the 4 in the sixes place now. In any base, adding something to 0 is easy.
\(103_{\text{six}} + 40_{\text{six}} = 143_{\text{six}}\)
So, combining our addends, we have \(2_{\text{six}} + 10_{\text{six}} + 40_{\text{six}} = 52_{\text{six}}\). This means \(51_{\text{six}} + 52_{\text{six}} = 143_{\text{six}}\), which means we now have our answer.
\(143_{\text{six}} – 51_{\text{six}} = 52_{\text{six}}\)
If you didn't follow that example, try reading it again but using base six blocks to model each step. Keep the numbers being added separate from the \(51_{\text{six}}\) so it's clear at the end what you added to the subtrahend to get the \(143_{\text{six}}\).
Using multibase blocks and a missing addend approach to perform the following operations.
- \(231_{\text{five}} – 140_{\text{five}}\)
- \(100_{\text{two}} – 11_{\text{two}}\)
- \(135_{\text{twelve}} – T6_{\text{twelve}}\)
The missing addend approach is sometimes called the Additive (or Austrian) Algorithm. This approach is very useful for doing subtraction on a number line.
Symmetry
Note that 8 + 4 = 12 is equivalent to 12 = 8 + 4. This is an example of the Symmetric Property of Equality.
The Symmetric Property of Equality states that for any equation, if \(a = b\), then it is also true that \(b = a\).
Therefore, it is perfectly okay to write the four facts in the Missing Addends portion above as the following.
| 2 + 6 = 8 |
| 6 + 2 = 8 |
| 8 – 2 = 6 |
| 8 – 6 = 2 |
Use the symmetric property of equality to rewrite each equation.
| a. 7 – 3 = 4 | b. 9 – 1 = 8 |
We like symmetry. But we cannot assume everything that we like is true. Consider the following.
Is there a symmetric property of inequality? Explain.
Hint: An example of an inequality is \(4 < 9\).


