5.4: Number Line Model

So far, we have focused on quantities that can be counted. For example, the population of humans on Earth at any given time may be known, but we know it's possible to count it. But not everything can be counted. Another way we often think about numbers is as abstract quantities that can be measured. For example, the length of a road, the area of a field, and the volume of a lake can all be measured, but not counted.

In a measurement model, you have to pick a basic unit. The basic unit is a quantity — such as length, area, or volume — that you assign to the number one. You can then assign numbers to other quantities based on how many of your basic unit fit inside.

For now, we’ll focus on length, and we’ll work with a number line where the basic unit is already marked off.

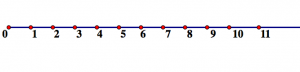
A number line continues "forever" in both directions, but we can only draw part of it. In the number line represented above, we see where 0, 1, 2, ..., and 11 are, but all the rest of the real numbers are on the line too. We just either cannot see them (such as -1 or 100) or they are not marked and explicitly labeled (like 1.5 or 12). Number lines are useful for showing relationships between sizes of numbers. For example, in the number line below, we can see a lot of things. We see that \( 0 < \frac{1}{5} < \frac{2}{5} < \frac{3}{5} < \frac{4}{5} < 1\) because numbers that are shown further to the right on a number line are larger than numbers shown further to the left. Note that this is only a convention. We the line need not be horizontal, and even if it is, we do not have to have the larger numbers on the right and smaller numbers on the left, for example. But once there are at least two numbers represented on the number line, we can see how it is oriented. Assuming we are not working in a different scale (for example, a logarithmic scale), we can then find all sorts of other numbers. For example, if I wanted to see where \(1 \frac{1}{5}\) is, I could just continue the line to the right of 1 using the line segment from \(0\) to \(\frac{1}{5}\) as a rule for how far to go.

We can also see that \(1\) is five times the size of \(\frac{1}{5}\) by noting that five copies of the line segment between \(0\) and \(\frac{1}{5}\) fit between 0 and 1.

Figure \(\PageIndex{1}\): A number line showing fifths between 0 and 1 (CC BY 4.0; Melissa Flora)

But we can do a lot more than just compare values. Number lines can also be used as tools to add and subtract.

Addition and Subtraction on the Number Line

Imagine a person — we’ll call him Zed — standing on a number line. We’ll say that the distance Zed walks when he takes a step is exactly one unit.

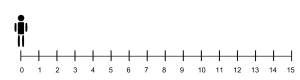
When Zed wants to add or subtract with whole numbers on the number line, he always starts at 0 and faces the positive direction (towards 1). On the number line above, this means he faces to the right. This is usually the positive direction for horizontal number lines. Then what he does depends on the calculation. Before continuing, it is a good idea to make a note of the fact that we are only dealing with nonnegative integers at this time. So, when we write "add two number", we mean "add two nonnegative integers".

If Zed wants to add two numbers, he walks forward (to the right of 0 on the number line) however many steps are indicated by the first number (the first addend). Then he walks forward (to your right on the number line) the number of steps indicated by the second number (the second addend). Where he lands is the sum of the two numbers.

Example \(\PageIndex{1}\)

How would Zed add 3+4 on the number line?

Solution:

If Zed wants to add 3 + 4, he starts at 0 and faces towards the positive numbers. He walks forward 3 steps, then he walks forward 4 more steps.

Zed ends at the number 7, so the sum of 3 and 4 is 7. 3 + 4 = 7. (But you knew that of course! The point right now is to make sense of the number line model.)

When Zed wants to subtract two numbers, he he walks forward (to the right on the number line) however many steps are indicated by the first number (the minuend). Then he walks backwards (to the left on the number line) the number of steps indicated by the second number (the subtrahend). Where he lands is the difference of the two numbers.

Example \(\PageIndex{1}\)

How would Zed subtract 11 – 3 on the number line?

Solution:

If Zed wants to subtract 11 – 3, he starts at 0 and faces the positive numbers (the right side of the number line). He walks forward 11 steps on the number line, then he walks backwards 3 steps.

Zed ends at the number 8, so the difference of 11 and 3 is 8. 11 – 3 = 8.

It's time for you to try some yourself. Actually draw a number line. Use a ruler to draw one that includes at least the numbers 0, 1, 2, ..., 15. 

Think / Pair / Share

• Work out each of these exercises on a number line.
  • 4 + 5
  • 6 + 9
  • 10 – 7
  • 8 – 1
• Why does it make sense to walk forward for addition and walk backwards for subtraction? In what way is this the same as “combining” for addition and “take away” for subtraction”? Once you think you can answer this, try telling a friend and see if they like your answer.
• What happens if you do these subtraction problems on a number line? Explain your answers.
  • 6 – 9
  • 1 – 7
  • 4 – 11
  • 0 – 1

Number Lines for Other Bases

We can use number lines with other bases to do addition and subtraction as well. If we can count in a base, then we can add or subtract. Consider the example below.

Example \(\PageIndex{1}\)

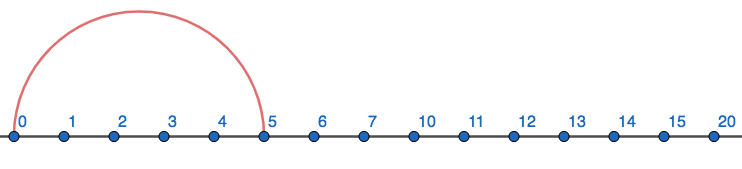
Use a number line to add \(5_{\text{eight}}+6_{\text{eight}}\).

Solution

The number line below shows numbers written in base eight. So, 10 on the number line is \(10_{\text{eight}}\), which is equal to 8 in the decimal system.

We begin by pretending to be Zed standing at 0 and moving to the right 5 steps.

Then, we pretend to be Zed adding \(6_{\text{eight\}}\) by taking 6 more steps to the right.

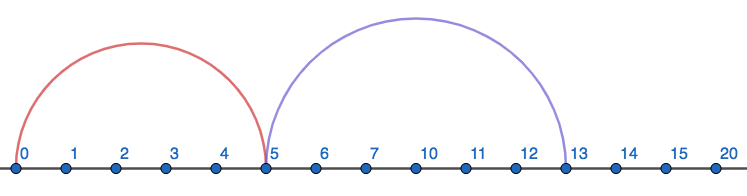
As we can see in the number line above, this means \(5_{\text{eight}}+6_{\text{eight}} = 13_{\text{eight}}\).

Let's try a subtraction problem.

Example \(\PageIndex{1}\)

Use a number line to subtract \(15_{\text{eight}} - 10_{\text{eight}}\).

Solution

Using the same base eight number line, we start by moving from \(0\) to \(15_{\text{eight}}\).

Now, since we need to subtract \(10_{\text{eight}}\) (which is equal to 8 in base ten!), we move to the left \(10_{\text{eight}}\) steps.

As we can see, this means \(15_{\text{eight}} - 10_{\text{eight}} = 5_{\text{eight}}\).

 Open Number Lines

An open number line (also called an empty number line) is a number line that starts with nothing on it, allowing the user to define the unit and pick a starting value as they see fit. They are especially useful when skip-counting.

Example \(\PageIndex{1}\)

Use an open number line to add \(182 + 20\).

Solution

We begin with just a line.

Since we know the first thing our friend Zed would have to do is take 182 steps from 0 to 182, we do not want to start by labeling 0, 1, 2, 3, etc. In fact, we won't bother labeling anything other than the two numbers we care about right now: 0 and 182. Since we know we will want to move further to the right (because we are adding a positive number to 182), we make sure to leave room to the right of 182.

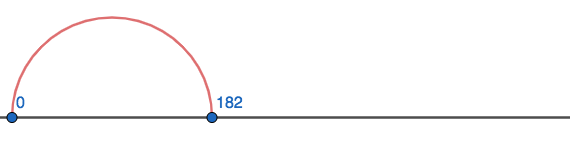
After we note where Zed would have ended up if he actually took all 182 of his steps, we know that he would take 20 more steps. It would be perfectly find to count out those 20 steps. But, in the effort to take less time counting by ones, we will imagine him taking just 2 big 10-step-long jumps.

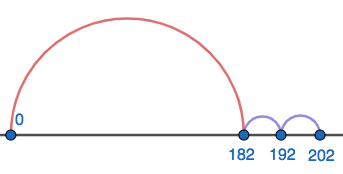
We can now see that \(182 + 20 = 202\).

The more efficient practice of making large jumps only works if the person using the number line has a good enough number sense. One way to develop such number sense is to use regular number lines and other tools.