8.3: Rational Numbers
- Page ID
- 132907
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)"Rational numbers" is simply the formal name for what people tend to call simply "fractions". The problem is that "fractions" is much more general. Below is a formal definition of a rational number.
A rational number is a real number that can be written as the quotient of an integer, \(m\), and a nonzero integer, \(n\), and is written as \(\frac{m}{n}\).
Note that another name for "quotient" is "ratio", which makes the use of the word "rational" a little more reasonable in this context.
To get a better understanding of this definition, let's look at a few numbers and determine if they are rational numbers.
Determine if each number is a rational number or not.
- \(-\frac{9}{2}\)
- \(100\)
- \(\frac{\pi}{2}\)
- \(\frac{\sqrt{-1}}{2}\)
Solution
The first two numbers are rational numbers, and the second two are not. Let's see why.
- \(-\frac{9}{2}\) can be written as a quotient of an integer and a nonzero integer. In this case, \(-\frac{9}{2} = \frac{-9}{2}\) works. Note that we could use a different quotient, such as \(\frac{9}{-2}\) or \(\frac{-27}{6}\).
- \(100\) can be written as a quotient of an integer and a nonzero integer. \(100 = \frac{100}{1}\) is the easiest way to see this. But, again, we could choose a different (though equivalent) quotient instead.
- \(\frac{\pi}{2}\) cannot be written as a quotient of an integer and a nonzero integer. The reason for this is that the number \(\pi\) is an irrational number. Johann Heinrich Lambert proved the irrationality of \(\pi\) in 1761 in "Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques".
- \(\frac{\sqrt{-1}}{2}\) is not even a real number, so it cannot be a rational number.
The point of the four numbers in the previous example is to make it clear that "rational number" and "fraction" are not interchangeable. 100 is not a fraction, but it can be written as one! \(\frac{\pi}{2}\) is a fraction, but it's not a fraction of an integer over a nonzero integer!
Parts of Wholes
So far, we have focused on fractions as the result of division (i.e., fractions are quotients). When the numerator and denominator must be integers means that we can use a part-whole definition of a fraction using discrete objects. We will stick with positive values and leave negative values to be defined as their "opposites". The following is one way to represent a rational number, \(\frac{m}{n}\).
Suppose \(m\) and \(n\) are positive integers. Given a defined whole (i.e., some object or set of objects that represents 1), which we call a unit, if the unit is divided into \(n\) equal parts, then each part represents the unit fraction \(\frac{1}{n}\). A collection of \(m\) copies of the parts represents the rational number \(\frac{m}{n}\).
Let's try this.
For each rational number, \(\frac{m}{n}\), do the following.
- Define a unit in terms of dots. State the value of each dot.
- Show a representation of \(\frac{1}{n}\).
- Show a representation of \(\frac{m}{n}\).
- Define the unit with a different number of dots, and do parts i and ii again.
- \(\frac{3}{8}\)
- \(\frac{2}{5}\)
Solution
\(\frac{3}{8}\)
- Define one unit to be the 8 dots below. Each dot represents 1/8.
• • • •
• • • •-
Below is a representation of 1/8.
•
-
Below is a representation of 3/8.
• • •
-
- Define one unit to be the 16 dots below. Each dot represents 1/16.
• • • •
• • • •
• • • •
• • • •-
In order to find 1/8, let's divide the whole into 8 equal portions. We will do this using brackets [ ] around dots. We need 8 sets of brackets.
[• •] [• •]
[• •] [• •]
[• •] [• •]
[• •] [• •]
Since there are 8 of them, one portion is 1/8. Below is a representation of 1/8.• •
-
Below is a representation of 3/8.
• • • •
• •
-
\(\frac{2}{5}\)
- Define one unit to be the 5 dots below. Each dot represents 1/5.
• • • • •
-
Below is a representation of 1/5.
•
-
Below is a representation of 2/5.
• •
-
- Define one unit to be the 10 dots below. Each dot represents 1/10.
• • • • •
• • • • •-
On your own, divide the whole into 5 equal portions. If you have done it correctly, each portion should have 2 dots. Below is a representation of 1/5.
• •
-
Below is a representation of 2/5.
• • • •
-
It is crucial to define your unit before beginning any exercise involving the representation of fractions! Try this on your own using dots to represent \(\frac{3}{4}\).
After you do this, see if you can answer these questions.
- Using this dots method of defining a unit, how many dots would you use in order to represent \(\frac{29}{100}\)?
- If you used a regular octagon as the unit instead, what would 1/8 be?
- What if you tried to use the same octagon as a unit but wanted to represent 1/5?
- What other ways can you represent units?
Comparing Fractions
We are now going to work again with dots (because they are easy to represent in a text document). This time we will use them to compare two fractions.
Use dot models to compare \(\frac{2}{5}\) and \(\frac{3}{7}\).
Solution
Note that we need a dot model that can work for both fifths and sevenths. We saw in the earlier example that fifths can be modeled with a unit consisting of 5 dots. But that would be difficult to use as the unit for dealing with sevenths. We also saw earlier that fifths can be modeled with a unit consisting of 10 dots. This still won't do it. You might have noticed that the reason 10 dots was chosen is because \(10 = 5\cdot 2\). You also probably figured out that the smallest number of dots used to model a fraction is based on the denominator, and we would probably start with 7 dots as the unit for representing sevenths. But that won't work for fifths! Using the fact that the multiple of 5 worked for fifths, we will try a multiple of both 5 and 7. Let's use \(5\cdot 7 = 35\) for our unit.
Let 1 unit be the 35 dots below.
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
That means each individual dot is 1/35 of a unit.
To find 1/5, we divide the collection into 5 equal portions. Notice that we can do this by simply using the rows.
[• • • • • • •]
[• • • • • • •]
[• • • • • • •]
[• • • • • • •]
[• • • • • • •]
Each row of 7 dots is 1/5 of the unit! In other words, 1/5 is represented below.
• • • • • • •
This means 2/5 is two copies of this. 2/5 is represented below.
• • • • • • •
• • • • • • •
To find 1/7, we divide the collection into 7 equal portions. Notice that we can do this by simply using the columns. Each column of 5 dots is 1/7 of the unit. In other words, 1/7 is represented below.
•
•
•
•
•
This means that 3/7 is 3 copies of this. 3/7 is represented below.
• • •
• • •
• • •
• • •
• • •
Now, we can compare them. We compare the 14 dots that form 2/5 with the 15 dots that form 3/7.
• • • • • • • • • •
• • • • • • • • • •
• • •
• • •
• • •
Since 14 is less than 15, we can see that it is reasonable to say that \(\frac{2}{5} < \frac{3}{7}\).
Try to use the process to do the following.
Compare 3/4 and 4/5 using dot models
Before moving on, notice that the method of finding the appropriate number of dots to use as the unit is similar to finding a common denominator. This is not just a coincidence!
Adding and Subtracting Fractions
We will continue to use our dots model method to add and subtract fractions, using add-to and take-from perspectives of addition and subtraction.
Use dot models to find the sum of \(\frac{2}{5}\) and \(\frac{3}{7}\).
Solution
As in the previous example, let's use 35 dots for the unit.
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
As before, 2/5 is represented below.
• • • • • • •
• • • • • • •
Similarly, 3/7 is represented below.
• • •
• • •
• • •
• • •
• • •
We will represent \(\frac{2}{5}+\frac{3}{7}\) by starting with the 14 dots that form 2/5 and then adding the 15 dots that form 3/7 to that. Let's start by just putting them together without thinking about how we represented the unit.
• • • • • • •
• • • • • • •
• • •
• • •
• • •
• • •
• • •
Now, we know that moving dots around does not change the number of dots and, thus, does not change the size of the portion we represent. So, let's move the lower dots up to form complete rows of 7 dots.
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • •
• • •
• • •
In short, \(\frac{2}{5}+\frac{3}{7}\) is represented below.
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
•
If we compare this to the unit, we see that this is 29 out of the 35 dots that form the unit.
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
Therefore, \(\frac{2}{5}+\frac{3}{7} = \frac{29}{35}\).
Try to use the process to do the following.
Use dot models to find the sum of \(\frac{1}{4}\) and \(\frac{2}{5}\).
Okay, let's go on to an example of subtraction.
Use dot models to find the difference of \(\frac{3}{7}\) and \(\frac{2}{5}\).
Solution
As in the previous examples, let's use 35 dots for the unit.
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
As before, 2/5 is represented below.
• • • • • • •
• • • • • • •
Similarly, 3/7 is represented below.
• • •
• • •
• • •
• • •
• • •
We will represent \(\frac{2}{5}-\frac{3}{7}\) by starting with the 15 dots that form 3/7 and then taking 14 dots that form 2/5 away from that. To do this, let's remind ourselves that we can rearrange dots. So, we will take the 14 dots that form 2/5 in columns of 5. So, now 2/5 is represented below.
• • •
• • •
• • •
• • •
• •
This makes it easier to see that when we take that away from 3/7, we have only one left!
• • •
• • •
• • •
• • •
• • •
In short, \(\frac{3}{7}-\frac{2}{5}\) is represented below.
•
If we compare this to the unit, we see that this is 1 out of the 35 dots that form the unit.
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
Therefore, \(\frac{3}{7}-\frac{2}{5} = \frac{1}{35}\).
Try to use the process to do the following.
Use dot models to subtract \(\frac{7}{8}-\frac{2}{3}\).
Multiplying Fractions
Multiplying fractions is a little bit trickier. This is partly because the repeated addition perspective (what we often think of as the simplest perspective of multiplication) doesn't make sense when you are multiplying two fractions. Instead, we will use the portion of a quantity perspective. When you see two fractions multiplied together, like \(\frac{2}{5} \cdot \frac{3}{7}\), think of it the first fraction of the second fraction. E.g., \(\frac{2}{5} \cdot \frac{3}{7}\) is 2/5 of 3/7. What does this mean? Part of the problem is we also need to think about what the fraction \(\frac{3}{7}\) means. That fraction means 3/7 of a unit. So, \(\frac{2}{5} \cdot \frac{3}{7}\) is actually 2/5 of 3/7 of a unit! That means to multiply \(\frac{2}{5} \cdot \frac{3}{7}\), you must take 3/7 of a unit and then take 2/5 of that.
Note that because of the way the English preposition "of" works, it makes sense that we have to first figure out what 3/7 is before dealing with the 2/5. Just like if you want to find "the brother of the best friend of Tom", you must find out who Tom's best friend is before you can even consider finding out who that person's brother is.
Use dot models to find the product of \(\frac{2}{5}\) and \(\frac{3}{7}\).
Solution
As in the previous examples, let's use 35 dots for the unit.
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
So, 3/7 of a unit is represented below.
• • •
• • •
• • •
• • •
• • •
We now need to find 2/5 of this! To do this, let's divide this portion into fifths. As before, since there are 5 rows of 3 in this representation of 3/7, each row of 3 is 1/5 of 3/7.
• • •
This means that 2/5 of 3/7 is 2 copies of that.
• • •
• • •
We now compare this to our unit.
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
Therefore, \(\frac{2}{5} \cdot frac{3}{7} = \frac{6}{35}\).
Okay, let's see what it looks like if we switch the order of the fractions.
Use dot models to find the product of \(\frac{3}{7}\) and \(\frac{2}{5}\).
Solution
We will start off the same, using 35 dots for the unit.
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
• • • • • • •
But now we need to know what 2/5 of the unit is. 2/5 of a unit is represented below.
• • • • • • •
• • • • • • •
We now need to find 3/7 of this. To do this, we divide this portion into sevenths. Since there are 7 rows of 2 in this representation of 2/5, each column of 2 is 1/7 of 2/5.
•
•
This means that 3/7 of 2/5 is 3 copies of that.
• • •
• • •
This is the same as what we got for \(\frac{2}{5} \cdot frac{3}{7}\).
Therefore, \(\frac{3}{7} \cdot frac{2}{5} = \frac{6}{35}\).
Although the answer is the same for the previous two examples, the sequence of steps is not. This is a reminder that the commutativity of multiplication is not obvious! Thinking of multiplication as the result of area helps, but we also must pair this with acceptance of the fact that all the perspectives of multiplication do, indeed, describe the same operation. This is also not obvious and is one of many reasons why people learning arithmetic for the first time need time and perseverance to build mathematical foundations. Speaking of perseverance, try to do the following on your own.
Use dot models to find the product of \(\frac{4}{5}\) and \(\frac{2}{3}\) and the product of \(\frac{3}{4}\) and \(\frac{5}{6}\).
One way to challenge yourself is to try working backwards.
Which multiplication is modeled below: \(\frac{1}{2} \cdot \frac{7}{8}\) or \(\frac{7}{8} \cdot \frac{1}{2}\)?
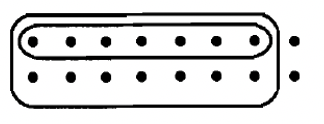
Solution
Notice that we see that the unit is represented with 16 dots.
• • • • • • • •
• • • • • • • •
14 of the dots are selected from the unit. These 14 dots consist of 7 columns of 2 dots each. Each column is 1/8 of the unit.
• • • • • • • •
• • • • • • • •
So, the 14 dots that are encircled represent 7 copies of 1/8. That is, they are 7/8 of the unit!
Then half of that selection is encircled. That's half of the 7/8. So, the inner-most encircled portion is 1/2 of 7/8 of the unit.
• • • • • • •
In other words, this models \(\frac{1}{2} \cdot \frac{7}{8} = \frac{7}{16}\).
Now try one on your own.
Which multiplication is modeled below: \(\frac{5}{6} \cdot \frac{2}{3}\) or \(\frac{2}{3} \cdot \frac{5}{6}\)?
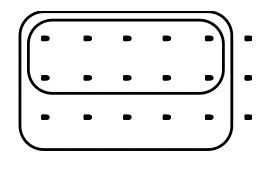
Dividing Fractions
To think about division with rational numbers, we can use the repeated subtraction (also called the measurement or quotitive) perspective of division. This perspective tells us that the quotient \(a \div b\) can be obtained by answering this question: "How many sets of \(b\) are contained in \(a\)?"
Use dot models to find the quotient of \(3\) and \(\frac{1}{2}\).
Solution
Since we will be caring about wholes and \(\frac{1}{2}\) of a whole, let's use two dots for a unit.
• •
So, \(3\), which is \(3\) copies of a unit, is represented below.
• •
• •
• •
On the other hand, \(\frac{1}{2}\) of a unit is represented below.
•
We want to know how many \(\frac{1}{2}\)s are in \(3\). Since \(\frac{1}{2}\) is •, that is the same as asking how many • are in the representation of \(3\) below.
• •
• •
• •
Clearly, there are 6. So, \(3 \div \frac{1}{2}=6\).
Let's do another, but this time involving fractions as both the divisor and the dividend. We will still keep it a little simple by only using unit fractions.
Use dot models to find the quotient of \(\frac{1}{2}\) and \(\frac{1}{4}\).
Solution
Since we will be caring about both 1/2 and 1/4, let's use four dots for a unit.
• • • •
So, 1/2 of a unit is represented below.
• •
On the other hand, 1/4 of a unit is represented below.
•
We want to know how many 1/4s are in 1/2. Since 1/4 is •, that is the same as asking how many • are in the representation of 1/2 below.
• •
Clearly, there are 2, so \(\frac{1}{2} \div \frac{1}{4} = 2\).
Try to do a similar problem on your own.
Use dot models to find \(\frac{1}{5} \div \frac{1}{10}\).
You might have noticed that this process seemed surprisingly easy compared to, say, multiplication. This is because we have still make this easier than in general. In particular, note that in the previous example and exercise, the denominator of the dividend is a factor of the denominator of the divisor. It turns out that was more important than the fact that the dividend was a unit fraction. It should be pretty straightforward to expand this method to perform division when we change the dividend to a non-unit fraction. Try the following.
Use dot models to find \(\frac{2}{3} \div \frac{1}{6}\)
To perform division in general may take a little more effort. The reason is that when we ask "How many \(b\) are in \(a\)?", the answer might not be an integer. There might be a nonzero remainder. Let's leave that for a later time though since we have already covered quite a bit!


