8.2: A Key Property of Fractions
- Page ID
- 132906
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We know that \(\frac{a}{b}\) is the answer to a division problem; for example, if \(a\) and \(b\) are both positive integers, then \(\frac{a}{b}\) represents the amount of pie an individual child receives when pies are shared equally by
children.
What happens if we double the number of pie and double the number of kids? Nothing! The amount of pie per child is still the same. In other words, we have the following fact.
\(\frac{2a}{2b} = \frac{a}{b}\)
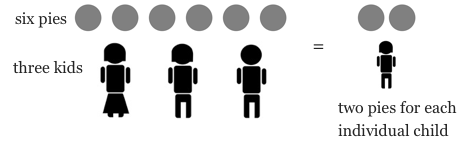
For example, as the picture shows, \(\frac{6}{3}\) and \(\frac{12}{6}\) both give two pies for each child.
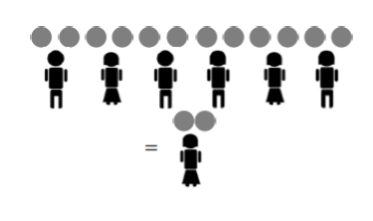
And tripling the number of pies and the number of children also does not change the final amount of pies per child, nor does quadrupling each number, or one trillion-billion-tupling the numbers!
\(\frac{6}{3} = \frac{12}{6} = \frac{18}{9} = \ldots =\) two pies per child}
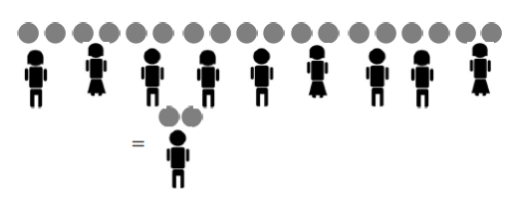
This leads us to want to believe what turns out to be a key property of fractions.
For any real numbers \(a\), \(b\), and \(x\) such that \(b \neq 0\) and \(x \neq 0\), \(\frac{xa}{xb} = \frac{a}{b}\).
Note that we have only thought about this for the special case where \(a\), \(b\), and \(x\) are positive integers; but it is actually true for many more possibilities.
We say that the fractions \(\frac{xa}{xb}\) and \(\frac{a}{b}\) are equivalent.
Write down at least 3 fractions equivalent to each of the following. Share your answers with another person and see if they agree that your answers are appropriate.
- \(\frac{1}{2}\)
- \(\frac{10}{3}\)
- 1
Note that in each case above, we started with smaller values in the numerator and denominator and then considered cases in which the values are larger. What if we went the other way.
\(\frac{20}{32}\) is the value equal to the amount an individual child gets when 32 kids share 20 pies.
This is the same result for when 8 kids share 5 pies.
\(\frac{20}{32} = \frac{5 \cdot 4}{8 \cdot 4} = \frac{5}{8}\)
Many people say we have cancelled the 4. Unfortunately, the word "cancelled" gets used for many situations in mathematics and can hide what is actually going on. It can also make it seem like we just get to take the 4 out because it's a weird trick or magic. Instead, the following phrases are better.
- \(\frac{20}{32} = \frac{5 \cdot 4}{8 \cdot 4} = \frac{5}{8}\)shows what happens when we divide out the common factor 4 from the numerator and denominator.
- \(\frac{20}{32} = \frac{5 \cdot 4}{8 \cdot 4} = \frac{5}{8}\) shows the process of reducing the fraction to lowest terms.
- \(\frac{20}{32} = \frac{5 \cdot 4}{8 \cdot 4} = \frac{5}{8}\) illustrates ;simplifying the fraction.
Each of these phrasings have advantages. It is a good idea to be comfortable with all of them and to try to use them instead of "cancelling".
As another example, \(\frac{280}{350}\) can certainly be simplified by noticing that there is a common factor of 10 in both the numerator and the denominator.
\(\frac{280}{350} = \frac{28 \cdot 10}{35 \cdot 10} = \frac{28}{35}\)
We can go further as 28 and 35 are both multiples of 7.
\(\frac{28}{35} = \frac{4 \cdot 7}{5 \cdot 7} = \frac{4}{5}\)
Thus, sharing 280 pies among 350 children gives the same result as sharing 4 pies among 5 children!
\(\frac{280}{350} = \frac{4}{5}\)
Since 4 and 5 share no common factors, this is as far as we can go with this example (while keeping the numerator and denominator equal to positive integers).
On Your Own
Mix and Match: Which simplified fraction goes with each non-simplified fraction fraction? (Notice that there are fewer simplified fractions than non-simplified frctions!)
|
|
See if you can come up with a good explanation for why all of this works. Then share it with another person and see if they believe your explanation.


