8.1: What is a Fraction?

Last updated
Save as PDF

Page ID: 132905

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

One of the things that makes fractions such a difficult concept to teach and to learn is that you have to think about them in a lot of different ways, depending on the problem at hand. For now, we are going to think of a fraction as the answer to a division problem.

Example: Pies Per child

Suppose 6 pies are to be shared equally among 3 children. This yields 2 pies per kid. We can abbreviate this as $\frac{6 \text{pies}}{3 \text{children}} = 2 \text{pies per child}$. Without the units, this is $\frac{6}{3} = 2$.

$"six pies" next to 6 circles above "three kids" next to three child icons = two circles above one child icon above "two pies for each individual child"$

The fraction $\frac{6}{3}$ is equivalent to the quotient $6 \div 3$, which equals 2. It represents the number of pies one whole child receives when three kids share six pies equally.

In the same way …

Sharing 10 pies among 2 kids yields $\frac{10}{2} = 5$ pies per kid.
Sharing 8 pies among 2 children yields $\frac{8}{2} = 4$ pies per child.
Sharing 5 pies among 5 kids yields $\frac{5}{5} = 1$ pie per kid.
Sharing 1 pie among 2 children yields $\frac{1}{2}$, which we call “one-half.”

This final example is actually saying something! It also represents how fractions are usually first taught to students:

If one pie is shared equally between two kids, then each child receives a portion of a pie which we choose to call “half.”

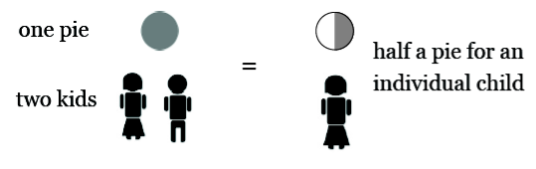
$"one pie" next to a circle above "two kids" next to 2 child icons = a half-shaded circle above a child icon next to "half a pie for an individual child"$

Thus students are taught to associate the number $`` \frac{1}{2} " $ to the picture $a half-shaded circle$ .

In the same way, the picture 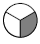$a third-shaded circle$ is said to represent “one-third,” that is, $\frac{1}{3}$. This is indeed the amount of pie an individual child would receive if one pie is shared among three. The picture $a fifth-shaded circle$ is called “one-fifth” and is indeed $\frac{1}{5}$, the amount of pie an individual receives if three pies are shared among five children. And the picture $a three-fifths-shaded circle$ is called “three-fifths”, which represents $\frac{3}{5}$, the amount of pie an individual receives if three pies are shared among five children.

Think / Pair / Share

Carefully explain to another person why this is true: If five kids share three pies equally, each child receives an amount that looks like this: $a three-fifths-shaded circle$ .

Your explanation will probably require both words and pictures.

On Your Own

Work on the following exercises on your own or with a partner.

Draw a picture associated with the fraction $\frac{1}{6}$.
Draw a picture associated with the fraction $\frac{3}{7}$. Is your picture really the amount of pie an individual would receive if three pies are shared among seven kids? Be very clear on this!
Let’s work backwards! Here’s the answer to a division problem:
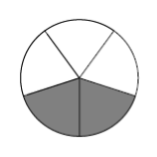
$a two-fifths-shaded circle$
This represents the amount of pie an individual kid receives if some number of pies is shared among some number of children. How many pies? How many children? How can you justify your answers?
Here’s another answer to a division problem:
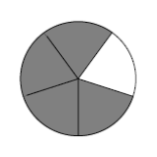
$a four-fifths-shaded circle$
How many pies? How many children? How can you justify your answers?
Here is another answer to a division problem:
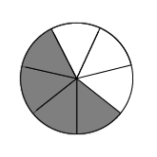
$a four-seventhsa-shaded circle$
How many pies? How many children? How can you justify your answers?
Leigh says that “$\frac{3}{5}$ is three times as big as $\frac{1}{5}$.” Is this right? Explain your answer.
Draw a picture for the answer to the division problem $\frac{4}{8}$. Describe what you notice about the answer.
Draw a picture for the answer to the division problem $\frac{2}{10}$. Describe what you notice about the answer.
What does the division problem $\frac{1}{1}$ represent? How much pie does an individual child receive?
What does the division problem $\frac{5}{1}$ represent? How much pie does an individual child receive?
What does the division problem $\frac{5}{5}$ represent? How much pie does an individual child receive?
Here is the answer to another division problem. This is the amount of pie an individual child receives:
$a shaded circle and a half-shaded circle$
How many pies were in the division problem? How many kids were in the division problem? Justify your answers.
Here is the answer to another division problem. This is the amount of pie an individual child receives:
$two shaded circles and one two-thirds-shaded circle$
How many pies were in the division problem? How many kids were in the division problem? Justify your answers
Many teachers have young students divide differently shaped pies into fractions. For example, a hexagonal pie is good for illustrating the fractions: $\frac{1}{6}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6}, \frac{5}{6},\; and\; \frac{6}{6} \ldotp$
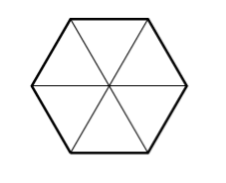
$a hexagon divided into 6 triangles$

Why is this shape used? What does $\frac{1}{6}$ of a pie look like?
What does $\frac{6}{6}$ of a pie look like?
What shape pie would be good for illustrating the fractions $\frac{1}{8}$ up to $\frac{8}{8}$?

Exercise 1

Some rectangular pies are distributed to some number of kids. This picture represents the amount of pie an individual child receives. The large rectangle represents one whole pie.

$a 7x5 shaded region of a rectangle split into 9x8 = 72 smaller rectangles$

How many pies? How many kids? Carefully justify your answers!

Pies Per Child Model

In our model, a fraction $\frac{a}{b}$ represents the amount of pie an individual child receives when $a$ pies are shared equally by $b$ kids. Of course, this only makes sense when $a$ and $b$ are both positive integers.

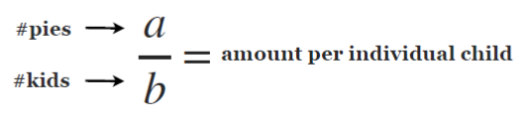
$a fraction a/b with the a labeled "#pies" and the b labeled "#kids" set equal to "amount per individual child"$

Try to answer the following questions and explain your answers to a friend or classmate.

Think / Pair / Share

What is $\frac{2}{2}$? What is $\frac{7}{7}$? What is $\frac{100}{100}$? How can you use the “Pies Per Child Model” to make sense of $\frac{a}{a}$ for any positive integer $a$?
What is $\frac{2}{1}$? What is $\frac{7}{1}$? What is $\frac{1876}{1}$? How can you use the “Pies Per Child Model” to make sense of $\frac{b}{1}$ for any positive integer $b$?
Write the answer to this division problem: “I have no pies to share among thirteen kids.” How can you generalize this division problem to make a general statement about fractions?

Before we continue, recall the following definitions so that we can use precise terminology.

Definition

For a fraction $\frac{a}{b}$, the top number $a$ is called the numerator of the fraction, and the bottom number $a$, is called the denominator of the fraction.

Many people insist that the numerator and denominator each be positive, but they do not have to be. Try to answer these questions below and explain your answers to a friend or classmate.

Think / Pair / Share

To understand why the numerator and denominator need not be integers, let's avoid discussing division of children and think about a plate of bacteria culture (which can be divided up however we please). Since the plate is circular, we will use a circle. Let's suppose the culture is red. So, the following will represent one whole plate of the culture.

$a red circle$

What would half a plate of the culture look like?
What would one-third of a plate of the culture look like?
What would three-fifths of a plate of the culture look like?

So, what would $\frac{1}{\left( \dfrac{1}{2} \right)}$ represent?

To answer that, we will consider what happens when we divide food among the bacteria culture. Let's say the bacteria get pellets of plant material to consume, which we will represent with a green rectangle.

$a green rectangle$

This means $\frac{1}{\left( \dfrac{1}{2} \right)}$ would be the result of dividing one pellet of plant material among a “group” of half a plate of the culture.

$a green rectangle$

$a red half-circle$

So how much would a whole plate of the culture receive? Well, since each half-place gets a full pellet, we can represent this as below.

$a green rectangle$ $a green rectangle$

$a red half-circle$ $a red half-circle$

But if we rotate the right half-circle around, we clearly get one whole circle. In other words, we have a whole plate of the culture.

$a green rectangle$ $a green rectangle$
$a red circle$

The whole plate of the bacteria culture gets two pellets. So, we have $\frac{1}{\left( \dfrac{1}{2} \right)} = \frac{2}{1} = 2$. Now try to answer the following using the pellets per plate of bacteria culture model. Try to explain each, possibly with pictures, to a friend or classmate.

Think / Pair / Share

Draw pictures for these problems if it helps!

What does $\frac{1}{\left( \dfrac{1}{3} \right)}$ represent?
What is $\frac{1}{\left( \dfrac{1}{6} \right)}$?
Explain why the fraction $\frac{5}{\left( \dfrac{1}{2} \right)$ represents the number 10.
What is $\frac{4}{\left( \dfrac{1}{3} \right)}$?
Challenge: Two-and-a-half pellets are to be shared equally among four-and-a-half plates of bacteria culture. How much of a pellet does a whole plate of culture receive?

Improper Fractions

A fraction with a numerator smaller than its denominator is called a proper fraction. For example, $\frac{45}{58}$ is “proper.”

A fraction with numerator larger than its denominator is called an improper fraction. For example, $\frac{7}{3}$ is “improper.”

For some reason, improper fractions are considered, well, improper by some teachers. So students are often asked to write improper fractions as a combination of a whole number and a proper fraction (often called “mixed numbers”). Despite their name, improper fractions are useful nonetheless!

With a mixed number, you have a good sense of the overall size of the number: “a little more than five,” or “a bit less than 17.”

Example: $\frac{7}{3}$

If seven pies are shared among three kids, then each kid will certainly receive two whole pies, leaving one pie to share among the three children.

$onepie-150x150.png$ $onepie-150x150.png$ $onepie-150x150.png$ $onepie-150x150.png$ $onepie-150x150.png$ $onepie-150x150.png$

$onekid2.png$ $onekid2.png$ $onekid.png$

Thus, $\frac{7}{3}$ equals 2 plus $\frac{1}{3}$. People write: $\frac{7}{3} = 2 \frac{1}{3}$ and call the result a mixed number. One can also write: $2 + \frac{1}{3}$, which is what $2 \frac{1}{3}$ really means. But most people choose to omit the plus sign.

But it is often easier to do calculations with improper fractions. Why do you think that is? This will be easier to answer once we learn more about calculating with fractions. But a hint for now is that it relates to the fact that there really is a hidden "+" between the integer and the fraction in a mixed number. So, think about what happens when you want to do calculations with a "number" that actually is itself a sum.

Students are often asked to memorize the names “proper fractions,” “improper fractions,” and “mixed number” so that they can follow directions. But, to a mathematician, these names are not at all important! There is no “correct” way to express an answer (assuming, that the answer is mathematically the right value). We often wish to express our answer in a "nicer" form, but sometimes the context will tell you what form is “nicer” and what form is more complicated.

Search

Text Color

Text Size

Margin Size

Font Type

Exercise 1

Think / Pair / Share

Definition

Think / Pair / Share

Think / Pair / Share

Example: \(\frac{7}{3}\)