5.3E: Exercises

Exercises

For each function in Exercises 1 - 10 below

• Find its domain.
• Create a sign diagram.
• Use your calculator to help you sketch its graph and identify any vertical or horizontal asymptotes, ‘unusual steepness’ or cusps.

1. \(f(x) = \sqrt{1 - x^{2}}\)
2. \(f(x) = \sqrt{x^2-1}\)
3. \(f(x) = x \sqrt{1-x^2}\)
4. \(f(x) = x \sqrt{x^2-1}\)
5. \(f(x) = \sqrt[4]{\dfrac{16x}{x^{2} - 9}}\)
6. \(f(x) = \dfrac{5x}{\sqrt[3]{x^{3} + 8}}\)
7. \(f(x) = x^{\frac{2}{3}}(x - 7)^{\frac{1}{3}}\)
8. \(f(x) = x^{\frac{3}{2}}(x - 7)^{\frac{1}{3}}\)
9. \(f(x) = \sqrt{x(x + 5)(x - 4)}\)
10. \(f(x) = \sqrt[3]{x^{3} + 3x^{2} - 6x - 8}\)

In Exercises 11 - 16, sketch the graph of \(y=g(x)\) by starting with the graph of \(y = f(x)\) and using the transformations presented in Section 1.7.

11. \(f(x) = \sqrt[3]{x}\), \(g(x) = \sqrt[3]{x-1}-2\)
12. \(f(x) = \sqrt[3]{x}\), \(g(x) = -2\sqrt[3]{x + 1} + 4\)
13. \(f(x) = \sqrt[4]{x}\), \(g(x) = \sqrt[4]{x-1}-2\)
14. \(f(x) = \sqrt[4]{x}\), \(g(x) = 3\sqrt[4]{x - 7} - 1\)
15. \(f(x) = \sqrt[5]{x}\), \(g(x) = \sqrt[5]{x + 2} + 3\)
16. \(f(x) = \sqrt[8]{x}\), \(g(x) = \sqrt[8]{-x} - 2\)

In Exercises 17 - 35, solve the equation or inequality.

17. \(x+1 = \sqrt{3x+7}\)
18. \(2x+1 = \sqrt{3-3x}\)
19. \(x + \sqrt{3x+10} = -2\)
20. \(3x+\sqrt{6-9x}=2\)
21. \(2x - 1 = \sqrt{x + 3}\)
22. \(x^{\frac{3}{2}} = 8\)
23. \(x^{\frac{2}{3}} = 4\)
24. \(\sqrt{x - 2} + \sqrt{x - 5} = 3\)
25. \(\sqrt{2x+1} = 3 + \sqrt{4-x}\)
26. \(5 - (4-2x)^{\frac{2}{3}} = 1\)
27. \(10-\sqrt{x-2} \leq 11\)
28. \(\sqrt[3]{x} \leq x\)
29. \(2 (x-2)^{-\frac{1}{3}} -\frac{2}{3} x(x-2)^{-\frac{4}{3}} \leq 0\)
30. \(-\frac{4}{3} (x-2)^{-\frac{4}{3}} + \frac{8}{9} x (x-2)^{-\frac{7}{3}} \geq 0\)
31. \(2x^{-\frac{1}{3}}(x-3)^{\frac{1}{3}} + x^{\frac{2}{3}} (x-3)^{-\frac{2}{3}} \geq 0\)
32. \(\sqrt[3]{x^{3} + 3x^{2} - 6x - 8} > x + 1\)
33. \(\frac{1}{3}x^{\frac{3}{4}}(x - 3)^{-\frac{2}{3}} + \frac{3}{4}x^{-\frac{1}{4}}(x - 3)^{\frac{1}{3}} < 0\)
34. \(x^{-\frac{1}{3}} (x-3)^{-\frac{2}{3}} - x^{-\frac{4}{3}} (x-3)^{-\frac{5}{3}} (x^2-3x+2) \geq 0\)
35. \(\frac{2}{3}(x + 4)^{\frac{3}{5}}(x - 2)^{-\frac{1}{3}} + \frac{3}{5}(x + 4)^{-\frac{2}{5}}(x - 2)^{\frac{2}{3}} \geq 0\)
36. Rework Example 5.3.3 so that the outpost is 10 miles from Route 117 and the nearest junction box is 30 miles down the road for the post.
37. The volume \(V\) of a right cylindrical cone depends on the radius of its base \(r\) and its height \(h\) and is given by the formula \(V = \frac{1}{3} \pi r^2 h\). The surface area \(S\) of a right cylindrical cone also depends on \(r\) and \(h\) according to the formula \(S = \pi r \sqrt{r^2+h^2}\). Suppose a cone is to have a volume of 100 cubic centimeters.
    1. Use the formula for volume to find the height \(h\) as a function of \(r\).
    2. Use the formula for surface area and your answer to 37a to find the surface area \(S\) as a function of \(r\).
    3. Use your calculator to find the values of \(r\) and \(h\) which minimize the surface area. What is the minimum surface area? Round your answers to two decimal places.
38. The National Weather Service uses the following formula to calculate the wind chill: \[W = 35.74 + 0.6215 \, T_{a} - 35.75\, V^{0.16} + 0.4275 \, T_{a} \, V^{0.16}\nonumber\] where \(W\) is the wind chill temperature in \(^{\circ}\)F, \(T_{a}\) is the air temperature in \(^{\circ}\)F, and \(V\) is the wind speed in miles per hour. Note that \(W\) is defined only for air temperatures at or lower than \(50^{\circ}\)F and wind speeds above \(3\) miles per hour.
    1. Suppose the air temperature is \(42^{\circ}\) and the wind speed is \(7\) miles per hour. Find the wind chill temperature. Round your answer to two decimal places.
    2. Suppose the air temperature is \(37^{\circ}\)F and the wind chill temperature is \(30^{\circ}\)F. Find the wind speed. Round your answer to two decimal places.
39. As a follow-up to Exercise 38, suppose the air temperature is \(28^{\circ}\)F.
    1. Use the formula from Exercise 38 to find an expression for the wind chill temperature as a function of the wind speed, \(W(V)\).
    2. Solve \(W(V) = 0\), round your answer to two decimal places, and interpret.
    3. Graph the function \(W\) using your calculator and check your answer to part 39b.
40. The period of a pendulum in seconds is given by \[T = 2\pi \sqrt{\dfrac{L}{g}}\nonumber\] (for small displacements) where \(L\) is the length of the pendulum in meters and \(g = 9.8\) meters per second per second is the acceleration due to gravity. My Seth-Thomas antique schoolhouse clock needs \(T = \frac{1}{2}\) second and I can adjust the length of the pendulum via a small dial on the bottom of the bob. At what length should I set the pendulum?
41. The Cobb-Douglas production model states that the yearly total dollar value of the production output \(P\) in an economy is a function of labor \(x\) (the total number of hours worked in a year) and capital \(y\) (the total dollar value of all of the stuff purchased in order to make things). Specifically, \(P = ax^{b}y^{1 - b}\). By fixing \(P\), we create what’s known as an ‘isoquant’ and we can then solve for \(y\) as a function of \(x\). Let’s assume that the Cobb-Douglas production model for the country of Sasquatchia is \(P = 1.23x^{0.4}y^{0.6}\).
    1. Let \(P = 300\) and solve for \(y\) in terms of \(x\). If \(x = 100\), what is \(y\)?
    2. Graph the isoquant \(300 = 1.23x^{0.4}y^{0.6}\). What information does an ordered pair \((x, y)\) which makes \(P = 300\) give you? With the help of your classmates, find several different combinations of labor and capital all of which yield \(P = 300\). Discuss any patterns you may see.
42. According to Einstein’s Theory of Special Relativity, the observed mass \(m\) of an object is a function of how fast the object is traveling. Specifically, \[m(x) = \dfrac{m_{r}}{\sqrt{1 - \dfrac{x^{2}}{c^{2}}}}\nonumber\] where \(m(0)=m_{r}\) is the mass of the object at rest, \(x\) is the speed of the object and \(c\) is the speed of light.
    1. Find the applied domain of the function.
    2. Compute \(m(.1c), \, m(.5c), \, m(.9c)\) and \(m(.999c)\).
    3. As \(x \rightarrow c^{-}\), what happens to \(m(x)\)?
    4. How slowly must the object be traveling so that the observed mass is no greater than 100 times its mass at rest?
43. Find the inverse of \(k(x) = \dfrac{2x}{\sqrt{x^{2} - 1}}\).
44. Suppose Fritzy the Fox, positioned at a point \((x,y)\) in the first quadrant, spots Chewbacca the Bunny at \((0,0)\). Chewbacca begins to run along a fence (the positive \(y\)-axis) towards his warren. Fritzy, of course, takes chase and constantly adjusts his direction so that he is always running directly at Chewbacca. If Chewbacca’s speed is \(v_{1}\) and Fritzy’s speed is \(v_{2}\), the path Fritzy will take to intercept Chewbacca, provided \(v_{2}\) is directly proportional to, but not equal to, \(v_{1}\) is modeled by

    \[y = \dfrac{1}{2} \left(\dfrac{x^{1+ v_{1}/v_{2}}}{1+v_1/v_2}- \dfrac{x^{1-v_1/v_2}}{1-v_1/v_2}\right) + \dfrac{v_1 v_2}{v_2^2-v_1^2}\]

    1. Determine the path that Fritzy will take if he runs exactly twice as fast as Chewbacca; that is, \(v_{2} = 2v_{1}\). Use your calculator to graph this path for \(x \geq 0\). What is the significance of the \(y\)-intercept of the graph?
    2. Determine the path Fritzy will take if Chewbacca runs exactly twice as fast as he does; that is, \(v_{1} = 2v_{2}\). Use your calculator to graph this path for \(x > 0\). Describe the behavior of \(y\) as \(x \rightarrow 0^{+}\) and interpret this physically.
    3. With the help of your classmates, generalize parts (a) and (b) to two cases: \(v_{2} > v_{1}\) and \(v_{2} < v_{1}\). We will discuss the case of \(v_{1} = v_{2}\) in Exercise 32 in Section 6.5.
45. Verify the Quotient Rule for Radicals in Theorem 5.3.1.
46. Show that \(\left(x^{\frac{3}{2}}\right)^{\frac{2}{3}} = x\) for all \(x \geq 0\).
47. Show that \(\sqrt[3]{2}\) is an irrational number by first showing that it is a zero of \(p(x) = x^{3} - 2\) and then showing \(p\) has no rational zeros. (You’ll need the Rational Zeros Theorem, Theorem 3.3.2, in order to show this last part.)
48. With the help of your classmates, generalize Exercise 47 to show that \(\sqrt[n]{c}\) is an irrational number for any natural numbers \(c \geq 2\) and \(n \geq 2\) provided that \(c \neq p^{n}\) for some natural number \(p\).

Answers

1. \(f(x) = \sqrt{1 - x^2}\)
   Domain: \([-1, 1]\)

   

   No asymptotes
   Unusual steepness at \(x = -1\) and \(x = 1\)
   No cusps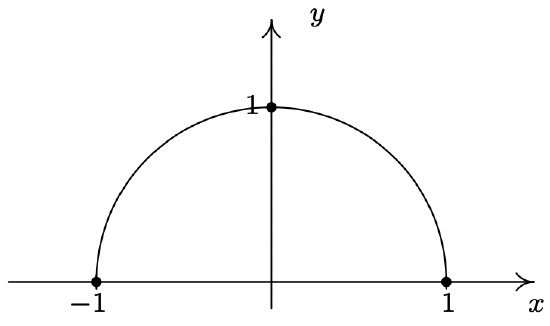

   

2. \(f(x) = \sqrt{x^2-1}\)
   Domain: \((-\infty, -1] \cup [1,\infty)\)

   

   No asymptotes
   Unusual steepness at \(x = -1\) and \(x = 1\)
   No cusps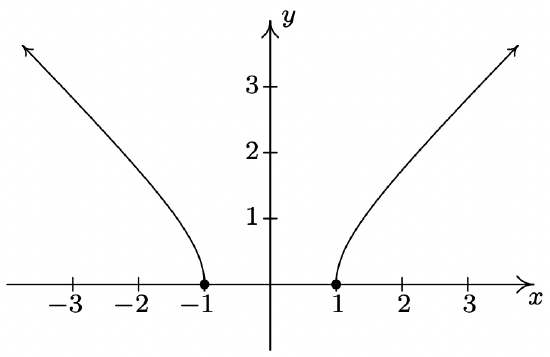

   

3. \(f(x) = x\sqrt{1-x^2}\)
   Domain: \([-1,1]\)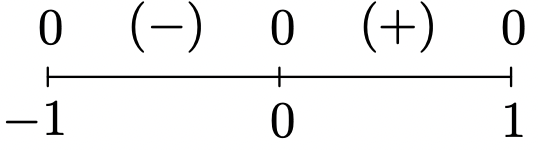

   

   No asymptotes
   Unusual steepness at \(x = -1\) and \(x = 1\)
   No cusps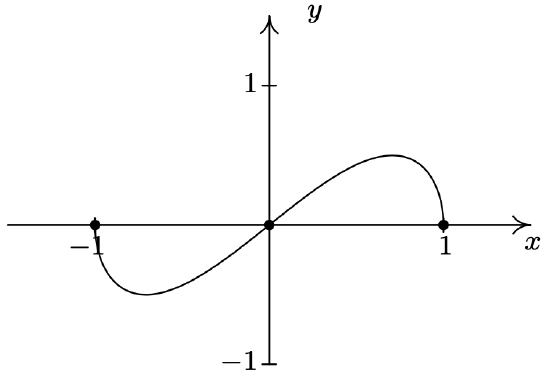

   

4. \(f(x) = x\sqrt{x^2-1}\)
   Domain: \((-\infty, -1] \cup [1,\infty)\)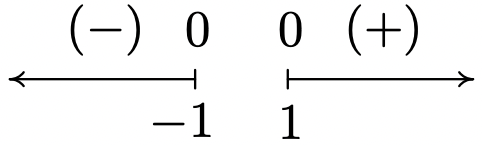

   

   No asymptotes
   Unusual steepness at \(x = -1\) and \(x = 1\)
   No cusps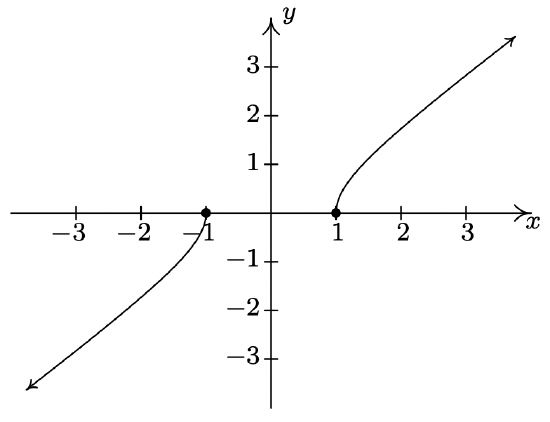

   

5. \(f(x) = \sqrt[4]{\dfrac{16x}{x^2 - 9}}\)
   Domain: \((-3, 0] \cup (3, \infty)\)

   

   Vertical asymptotes: \(x = -3\) and \(x = 3\)
   Horizontal asymptote: \(y = 0\)
   Unusual steepness at \(x = 0\)
   No cusps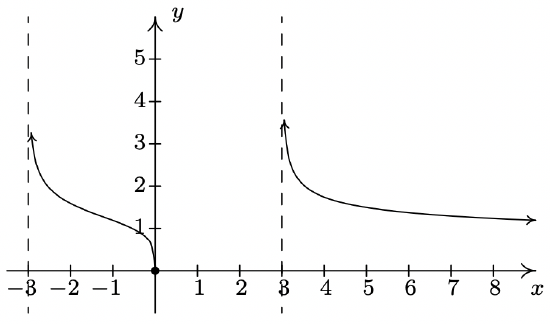

   

6. \(f(x) = \dfrac{5x}{\sqrt[3]{x^{3} + 8}}\)
   Domain: \((-\infty, -2) \cup (-2, \infty)\)

   

   Vertical asymptote \(x = -2\)
   Horizontal asymptote \(y = 5\)
   No unusual steepness or cusps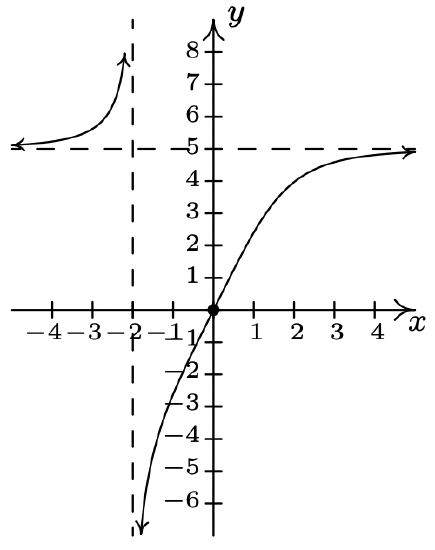

   

7. 2 \(f(x) = x^{\frac{2}{3}}(x - 7)^{\frac{1}{3}}\)
   Domain: \((-\infty, \infty)\)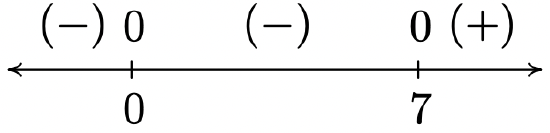

   

   No vertical or horizontal asymptotes¹³
   Unusual steepness at \(x = 7\)
   Cusp at \(x = 0\)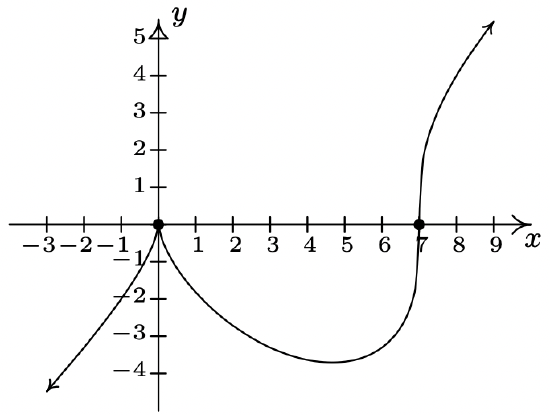

   

8. \(f(x) = x^{\frac{3}{2}}(x - 7)^{\frac{1}{3}}\)
   Domain: \([0, \infty)\)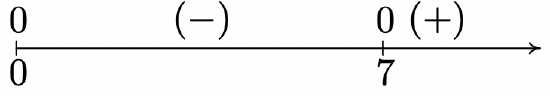

   

   No asymptotes
   Unusual steepness at \(x = 7\)
   No cusps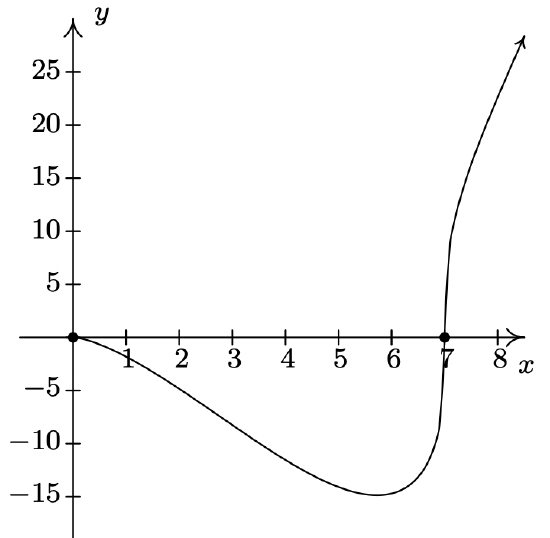

   

9. \(f(x) = \sqrt{x(x + 5)(x - 4)}\)
   Domain: \([-5, 0] \cup [4, \infty)\)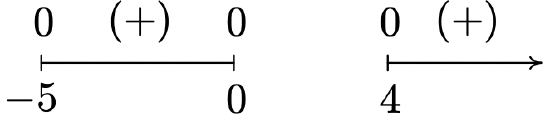

   

   No asymptotes
   Unusual steepness at \(x = -5, x = 0\) and \(x = 4\)
   No cusps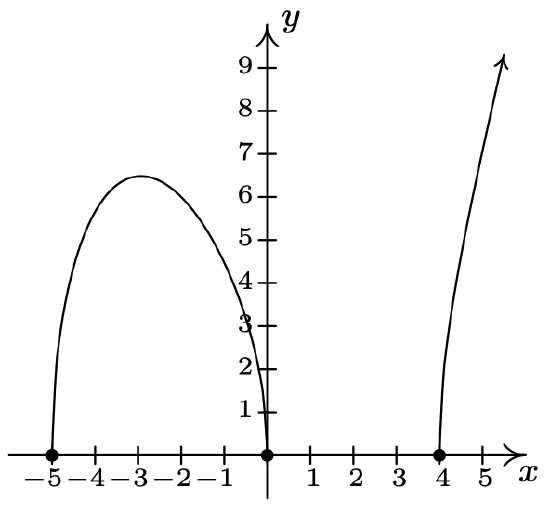

   

10. 2 \(f(x) = \sqrt[3]{x^{3} + 3x^{2} - 6x - 8}\)
    Domain: \((-\infty, \infty)\)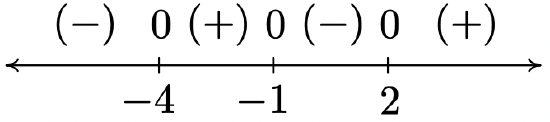

    

    No vertical or horizontal asymptotes¹⁴
    Unusual steepness at \(x = -4, x = -1\) and \(x = 2\)
    No cusps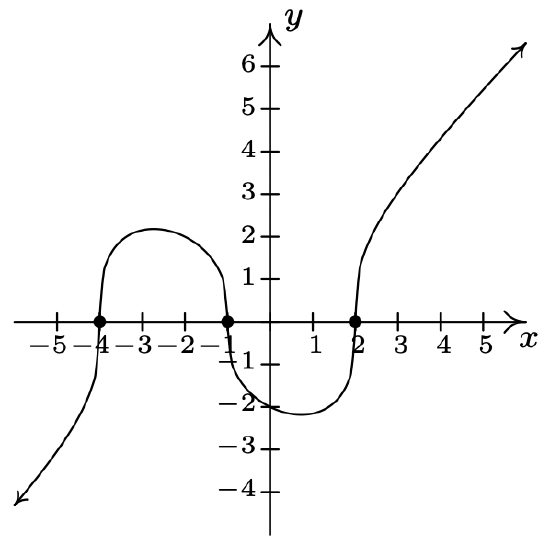

    

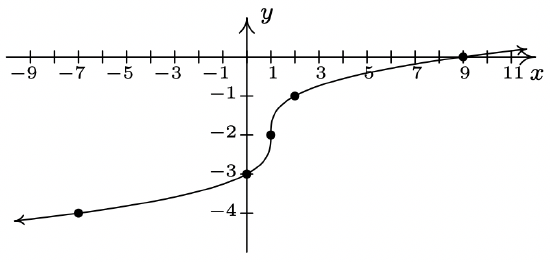
11. \(g(x) = \sqrt[3]{x-1}-2\)

    

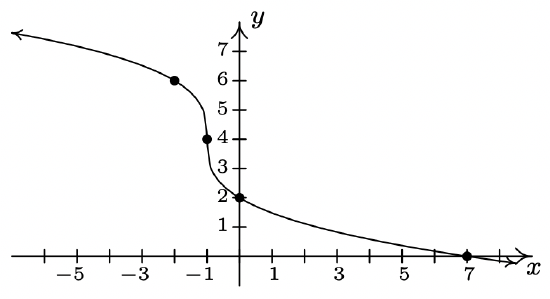
12. \(g(x) = -2\sqrt[3]{x + 1} + 4\)

    

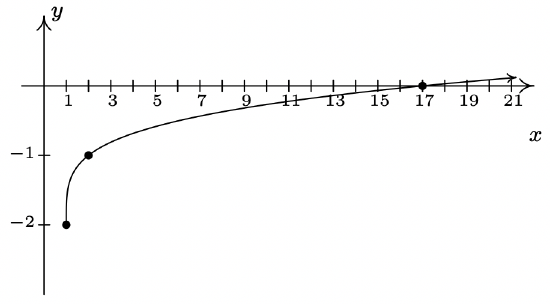
13. \(g(x) = \sqrt[4]{x-1}-2\)

    

14. \(g(x) = 3\sqrt[4]{x - 7} - 1\)

    

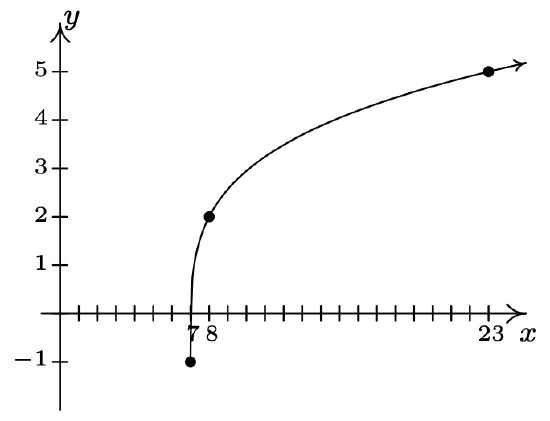
15. \(g(x) = \sqrt[5]{x + 2} + 3\)

    

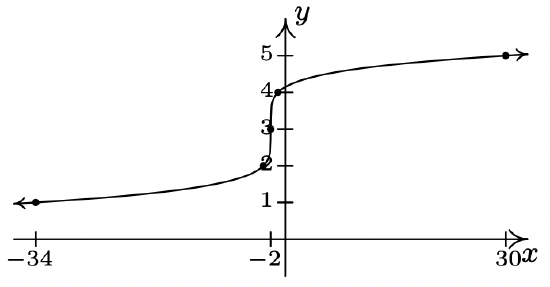
16. \(g(x) = \sqrt[8]{-x} - 2\)

    

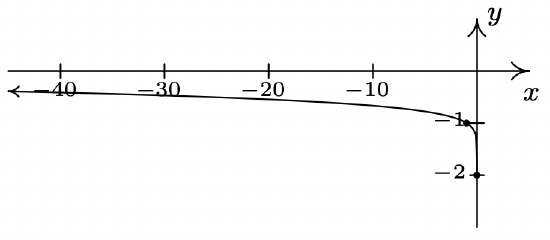
17. \(x=3\)
18. \(x = \frac{1}{4}\)
19. \(x=-3\)
20. \(x = -\frac{1}{3}, \; \frac{2}{3}\)
21. \(x = \frac{5 + \sqrt{57}}{8}\)
22. \(x = 4\)
23. \(x = \pm 8\)
24. \(x = 6\)
25. \(x = 4\)
26. \(x=-2, 6\)
27. \([2, \infty)\)
28. \([-1, 0] \cup [1, \infty)\)
29. \((-\infty, 2) \cup (2,3]\)
30. \((2,6]\)
31. \((-\infty, 0) \cup [2,3) \cup (3, \infty)\)
32. \((-\infty, -1)\)
33. \(\left(0, \frac{27}{13} \right)\)
34. \((-\infty, 0) \cup (0,3)\)
35. \((-\infty, -4) \cup \left(-4, -\frac{22}{19}\right] \cup (2, \infty)\)
36. \(C(x) = 15x+20\sqrt{100+(30-x)^2}\), \(0 \leq x \leq 30\). The calculator gives the absolute minimum at \(\approx (18.66, 582.29)\). This means to minimize the cost, approximately 18.66 miles of cable should be run along Route 117 before turning off the road and heading towards the outpost. The minimum cost to run the cable is approximately \(\$582.29\).
37. 1. \(h(r) = \frac{300}{\pi r^2}\), \(r > 0\).
    2. \(S(r) = \pi r \sqrt{r^2+\left(\frac{300}{\pi r^2}\right)^2} = \frac{\sqrt{\pi^2 r^6+90000}}{r}\), \(r>0\)
    3. The calculator gives the absolute minimum at the point \(\approx (4.07, 90.23)\). This means the radius should be (approximately) 4.07 centimeters and the height should be 5.76 centimeters to give a minimum surface area of 90.23 square centimeters.
38. 1. \(W \approx 37.55^{\circ}\)F.
    2. \(V \approx 9.84\) miles per hour.
39. 1. \(W(V) = 53.142 - 23.78 V^{0.16}\). Since we are told in Exercise 38 that wind chill is only effect for wind speeds of more than 3 miles per hour, we restrict the domain to \(V > 3\).
    2. \(W(V)=0\) when \(V \approx 152.29\). This means, according to the model, for the wind chill temperature to be \(0^{\circ}\)F, the wind speed needs to be \(152.29\) miles per hour.
    3. The graph is below.

       

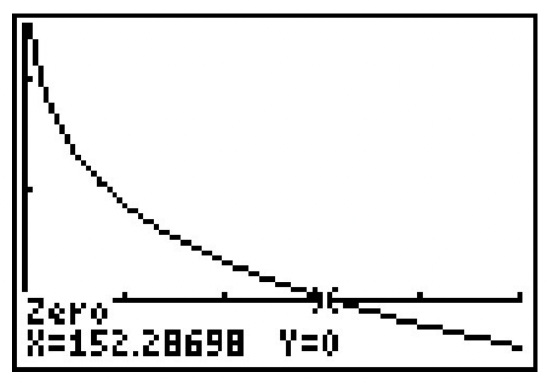
40. \(9.8 \left(\dfrac{1}{4\pi}\right)^{2} \approx 0.062\) meters or \(6.2\) centimeters
41. 1. First rewrite the model as \(P = 1.23x^{\frac{2}{5}}y^{\frac{3}{5}}\). Then \(300 = 1.23x^{\frac{2}{5}}y^{\frac{3}{5}}\) yields \(y = \left( \dfrac{300}{1.23x^{\frac{2}{5}}} \right)^{\frac{5}{3}}\). If \(x = 100\) then \(y \approx 441.93687\).
42. 1. \([0, c)\)
    2. \(\begin{aligned}
       &m(.1 c)=\frac{m_{r}}{\sqrt{.99}} \approx 1.005 m_{r} \quad m(.5 c)=\frac{m_{r}}{\sqrt{.75}} \approx 1.155 m_{r} \\
       &m(.9 c)=\frac{m_{r}}{\sqrt{.19}} \approx 2.294 m_{r} \quad m(.999 c)=\frac{m_{r}}{\sqrt{.0 .001999}} \approx 22.366 m_{r}
       \end{aligned}\)
    3. As \(x \rightarrow c^{-}, \, m(x) \rightarrow \infty\)
    4. If the object is traveling no faster than approximately \(0.99995\) times the speed of light, then its observed mass will be no greater than \(100m_{r}\).
43. \(k^{-1}(x) = \dfrac{x}{\sqrt{x^{2} - 4}}\)
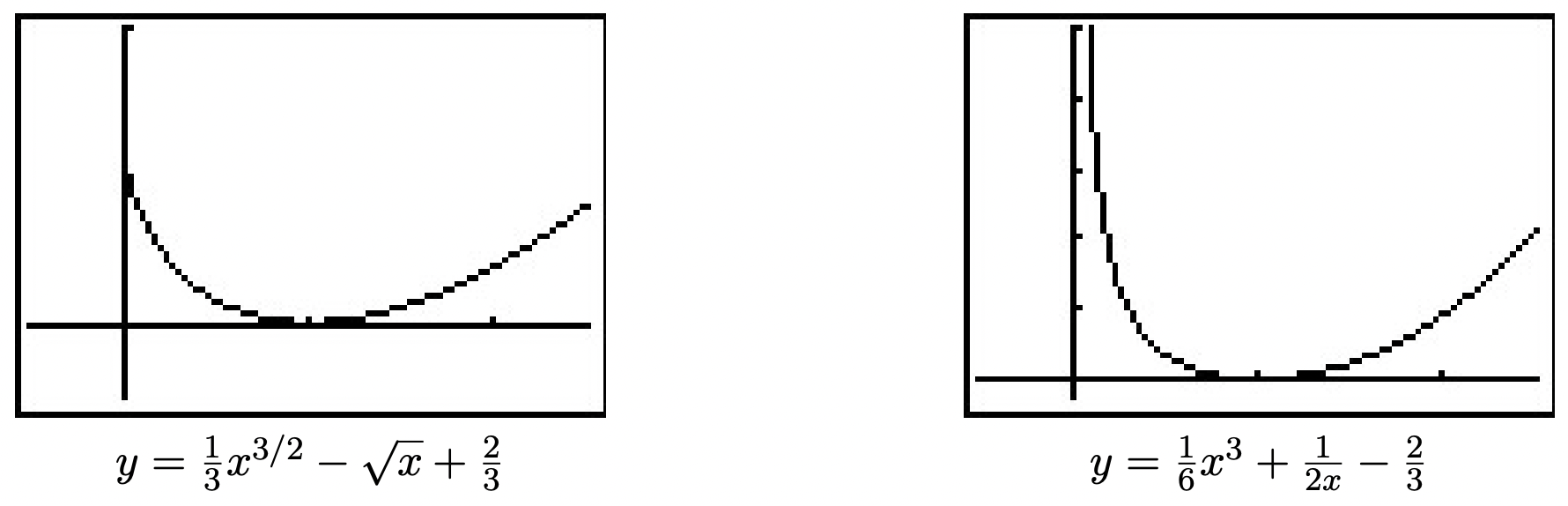
44. 1. \(y = \frac{1}{3}x^{3/2} - \sqrt{x} + \frac{2}{3}\). The point \(\left(0,\frac{2}{3}\right)\) is when Fritzy’s path crosses Chewbacca’s path - in other words, where Fritzy catches Chewbacca.
    2. \(y = \frac{1}{6}x^3+\frac{1}{2x} - \frac{2}{3}\). Using the techniques from Chapter 4, we find as \(x \rightarrow 0^{+}\), \(y \rightarrow \infty\) which means, in this case, Fritzy’s pursuit never ends; he never catches Chewbacca. This makes sense since Chewbacca has a head start and is running faster than Fritzy.