6.5E: Exercises

Exercises

For each of the scenarios given in Exercises 1 - 6,

• Find the amount \(A\) in the account as a function of the term of the investment \(t\) in years.
• Determine how much is in the account after \(5\) years, \(10\) years, \(30\) years and \(35\) years. Round your answers to the nearest cent.
• Determine how long will it take for the initial investment to double. Round your answer to the nearest year.
• Find and interpret the average rate of change of the amount in the account from the end of the fourth year to the end of the fifth year, and from the end of the thirty-fourth year to the end of the thirty-fifth year. Round your answer to two decimal places.

1. \(\$500\) is invested in an account which offers \(0.75 \%\), compounded monthly.
2. \(\$500\) is invested in an account which offers \(0.75 \%\), compounded continuously.
3. \(\$1000\) is invested in an account which offers \(1.25 \%\), compounded monthly.
4. \(\$1000\) is invested in an account which offers \(1.25 \%\), compounded continuously.
5. \(\$5000\) is invested in an account which offers \(2.125 \%\), compounded monthly.
6. \(\$5000\) is invested in an account which offers \(2.125 \%\), compounded continuously.
7. Look back at your answers to Exercises 1 - 6. What can be said about the difference between monthly compounding and continuously compounding the interest in those situations? With the help of your classmates, discuss scenarios where the difference between monthly and continuously compounded interest would be more dramatic. Try varying the interest rate, the term of the investment and the principal. Use computations to support your answer.
8. How much money needs to be invested now to obtain \(\$2000\) in 3 years if the interest rate in a savings account is \(0.25 \%\), compounded continuously? Round your answer to the nearest cent.
9. How much money needs to be invested now to obtain \(\$5000\) in 10 years if the interest rate in a CD is \(2.25 \%\), compounded monthly? Round your answer to the nearest cent.
10. On May, 31, 2009, the Annual Percentage Rate listed at Jeff’s bank for regular savings accounts was \(0.25\%\) compounded monthly.
    1. If \(P = 2000\) what is \(A(8)\)?
    2. Solve the equation \(A(t) = 4000\) for \(t\).
    3. What principal \(P\) should be invested so that the account balance is $2000 is three years?
11. Jeff’s bank also offers a 36-month Certificate of Deposit (CD) with an APR of \(2.25\%\).
    1. If \(P = 2000\) what is \(A(8)\)?
    2. Solve the equation \(A(t) = 4000\) for \(t\).
    3. What principal \(P\) should be invested so that the account balance is $2000 in three years?
    4. The Annual Percentage Yield is the interest rate that returns the same amount of interest after one year as the compound interest does. With the help of your classmates, compute the APY for this investment.
12. A finance company offers a promotion on \(\$5000\) loans. The borrower does not have to make any payments for the first three years, however interest will continue to be charged to the loan at \(29.9 \%\) compounded continuously. What amount will be due at the end of the three year period, assuming no payments are made? If the promotion is extended an additional three years, and no payments are made, what amount would be due?
13. Show that the time it takes for an investment to double in value does depend on the principal \(P\), but rather, depends only on the APR and the number of compoundings per year. Let \(n = 12\) and with the help of your classmates compute the doubling time for a variety of rates \(r\). Then look up the Rule of 72 and compare your answers to what that rule says. If you’re really interested in Financial Mathematics, you could also compare and contrast the Rule of 72 with the Rule of 70 and the Rule of 69.

In Exercises 14 - 18, we list some radioactive isotopes and their associated half-lives. Assume that each decays according to the formula \(A(t)=A_{0} e^{k t}\) where \(A_{0}\) is the initial amount of the material and \(k\) is the decay constant. For each isotope:

• Find the decay constant \(k\). Round your answer to four decimal places.
• Find a function which gives the amount of isotope \(A\) which remains after time \(t\). (Keep the units of \(A\) and \(t\) the same as the given data.)
• Determine how long it takes for \(90 \%\) of the material to decay. Round your answer to two decimal places. (HINT: If \(90 \%\) of the material decays, how much is left?)

14. Cobalt 60, used in food irradiation, initial amount 50 grams, half-life of \(5.27\) years.
15. Phosphorus 32, used in agriculture, initial amount 2 milligrams, half-life \(14\) days.
16. Chromium 51, used to track red blood cells, initial amount 75 milligrams, half-life \(27.7\) days.
17. Americium 241, used in smoke detectors, initial amount 0.29 micrograms, half-life \(432.7\) years.
18. Uranium 235, used for nuclear power, initial amount \(1\) kg grams, half-life \(704\) million years.
19. With the help of your classmates, show that the time it takes for \(90 \%\) of each isotope listed in Exercises 14 - 18 to decay does not depend on the initial amount of the substance, but rather, on only the decay constant \(k\). Find a formula, in terms of \(k\) only, to determine how long it takes for \(90 \%\) of a radioactive isotope to decay.
20. In Example 6.1.2 in Section 6.1, the exponential function \(V(x) = 25 \left(\frac{4}{5}\right)^{x}\) was used to model the value of a car over time. Use the properties of logs and/or exponents to rewrite the model in the form \(V(t) = 25e^{kt}\).
21. The Gross Domestic Product (GDP) of the US (in billions of dollars) \(t\) years after the year 2000 can be modeled by: \[G(t) = 9743.77 e^{0.0514t}\nonumber\]
    1. Find and interpret \(G(0)\).
    2. According to the model, what should have been the GDP in 2007? In 2010? (According to the US Department of Commerce, the 2007 GDP was \(\$14,369.1\) billion and the 2010 GDP was \(\$14,657.8\) billion.)
22. The diameter \(D\) of a tumor, in millimeters, \(t\) days after it is detected is given by: \[D(t) = 15e^{0.0277t}\nonumber\]
    1. What was the diameter of the tumor when it was originally detected?
    2. How long until the diameter of the tumor doubles?
23. Under optimal conditions, the growth of a certain strain of E. Coli is modeled by the Law of Uninhibited Growth \(N(t)=N_{0} e^{k t}\) where \(N_{0}\) is the initial number of bacteria and \(t\) is the elapsed time, measured in minutes. From numerous experiments, it has been determined that the doubling time of this organism is 20 minutes. Suppose 1000 bacteria are present initially.
    1. Find the growth constant \(k\). Round your answer to four decimal places.
    2. Find a function which gives the number of bacteria \(N(t)\) after \(t\) minutes.
    3. How long until there are 9000 bacteria? Round your answer to the nearest minute.
24. Yeast is often used in biological experiments. A research technician estimates that a sample of yeast suspension contains 2.5 million organisms per cubic centimeter (cc). Two hours later, she estimates the population density to be 6 million organisms per cc. Let \(t\) be the time elapsed since the first observation, measured in hours. Assume that the yeast growth follows the Law of Uninhibited Growth \(N(t)=N_{0} e^{k t}\).
    1. Find the growth constant \(k\). Round your answer to four decimal places.
    2. Find a function which gives the number of yeast (in millions) per cc \(N(t)\) after \(t\) hours.
    3. What is the doubling time for this strain of yeast?
25. The Law of Uninhibited Growth also applies to situations where an animal is re-introduced into a suitable environment. Such a case is the reintroduction of wolves to Yellowstone National Park. According to the National Park Service, the wolf population in Yellowstone National Park was 52 in 1996 and 118 in 1999. Using these data, find a function of the form \(N(t)=N_{0} e^{k t}\) which models the number of wolves \(t\) years after 1996. (Use \(t = 0\) to represent the year 1996. Also, round your value of \(k\) to four decimal places.) According to the model, how many wolves were in Yellowstone in 2002? (The recorded number is 272.)
26. During the early years of a community, it is not uncommon for the population to grow according to the Law of Uninhibited Growth. According to the Painesville Wikipedia entry, in 1860, the Village of Painesville had a population of 2649. In 1920, the population was 7272. Use these two data points to fit a model of the form \(N(t)=N_{0} e^{k t}\) were \(N(t)\) is the number of Painesville Residents \(t\) years after 1860. (Use \(t = 0\) to represent the year 1860. Also, round the value of \(k\) to four decimal places.) According to this model, what was the population of Painesville in 2010? (The 2010 census gave the population as 19,563) What could be some causes for such a vast discrepancy? For more on this, see Exercise 37.
27. The population of Sasquatch in Bigfoot county is modeled by \[P(t) = \dfrac{120}{1 + 3.167e^{-0.05t}}\nonumber\] where \(P(t)\) is the population of Sasquatch \(t\) years after \(2010\).
    1. Find and interpret \(P(0)\).
    2. Find the population of Sasquatch in Bigfoot county in 2013. Round your answer to the nearest Sasquatch.
    3. When will the population of Sasquatch in Bigfoot county reach 60? Round your answer to the nearest year.
    4. Find and interpret the end behavior of the graph of \(y = P(t)\). Check your answer using a graphing utility.
28. The half-life of the radioactive isotope Carbon-14 is about 5730 years.
    1. Express the amount of Carbon-14 left from an initial \(N\) milligrams as a function of time \(t\) in years.
    2. What percentage of the original amount of Carbon-14 is left after 20,000 years?
    3. If an old wooden tool is found in a cave and the amount of Carbon-14 present in it is estimated to be only 42% of the original amount, approximately how old is the tool?
    4. Radiocarbon dating is not as easy as these exercises might lead you to believe. With the help of your classmates, research radiocarbon dating and discuss why our model is somewhat over-simplified.
29. Carbon-14 cannot be used to date inorganic material such as rocks, but there are many other methods of radiometric dating which estimate the age of rocks. One of them, Rubidium-Strontium dating, uses Rubidium-87 which decays to Strontium-87 with a half-life of 50 billion years. Express the amount of Rubidium-87 left from an initial 2.3 micrograms as a function of time \(t\) in billions of years. Research this and other radiometric techniques and discuss the margins of error for various methods with your classmates.
30. Show that \(k = -\dfrac{\ln(2)}{h}\) where \(h\) is the half-life of the radioactive isotope.
31. A pork roast was taken out of a hardwood smoker when its internal temperature had reached \(180^{\circ}\)F and it was allowed to rest in a \(75^{\circ}\)F house for 20 minutes after which its internal temperature had dropped to \(170^{\circ}\)F. Assuming that the temperature of the roast follows Newton’s Law of Cooling,
    1. Express the temperature \(T\) (in \(^{\circ}\)F) as a function of time \(t\) (in minutes).
    2. Find the time at which the roast would have dropped to \(140^{\circ}\)F had it not been carved and eaten.
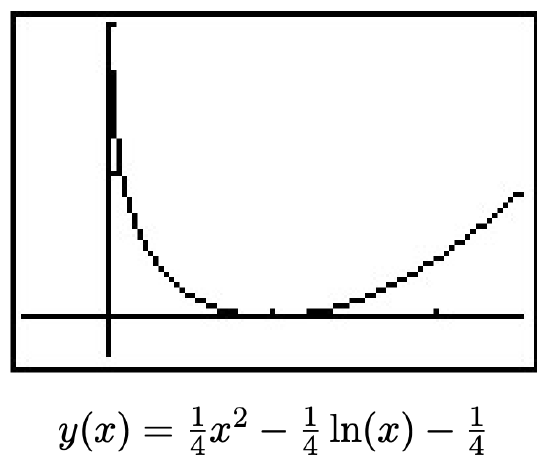
32. In reference to Exercise 44 in Section 5.3, if Fritzy the Fox’s speed is the same as Chewbacca the Bunny’s speed, Fritzy’s pursuit curve is given by

    \[y(x) = \frac{1}{4} x^2-\frac{1}{4} \ln(x)-\frac{1}{4}\nonumber\]

    Use your calculator to graph this path for \(x > 0\). Describe the behavior of \(y\) as \(x \rightarrow 0^{+}\) and interpret this physically.

33. The current \(i\) measured in amps in a certain electronic circuit with a constant impressed voltage of 120 volts is given by \(i(t) = 2 - 2e^{-10t}\) where \(t \geq 0\) is the number of seconds after the circuit is switched on. Determine the value of \(i\) as \(t \rightarrow \infty\). (This is called the steady state current.)
34. If the voltage in the circuit in Exercise 33 above is switched off after 30 seconds, the current is given by the piecewise-defined function

    \[i(t) = \left\{ \begin{array}{rcl} 2 - 2e^{-10t} & \mbox{if} & 0 \leq t < 30 \\ [6pt] \left(2 - 2e^{-300}\right) e^{-10t+300} & \mbox{if} & t \geq 30 \end{array} \right.\nonumber\]

    With the help of your calculator, graph \(y = i(t)\) and discuss with your classmates the physical significance of the two parts of the graph \(0 \leq t < 30\) and \(t \geq 30\).

35. A free hanging cable forms a basic shape is given by \(y = \frac{1}{2}\left(e^{x} + e^{-x}\right)\). Use your calculator to graph this function. What are its domain and range? What is its end behavior? Is it invertible? How do you think it is related to the function given in Exercise 47 in Section 6.3 and the one given in the answer to Exercise 38 in Section 6.4? When flipped upside down, the catenary makes an arch. The Gateway Arch in St. Louis, Missouri has the shape \[y = 757.7 - \frac{127.7}{2}\left(e^{\frac{x}{127.7}} + e^{-\frac{x}{127.7}}\right)\nonumber\] where \(x\) and \(y\) are measured in feet and \(-315 \leq x \leq 315\). Find the highest point on the arch.
36. In Exercise 6a in Section 2.5, we examined the data set given below which showed how two cats and their surviving offspring can produce over 80 million cats in just ten years. It is virtually impossible to see this data plotted on your calculator, so plot \(x\) versus \(\ln(x)\) as was done on page 480. Find a linear model for this new data and comment on its goodness of fit. Find an exponential model for the original data and comment on its goodness of fit.

    \(\begin{array}{|l|r|r|r|r|r|r|r|r|r|r|}
    \hline \text { Year } x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & & 9 \\
    \hline \text { Number of } & & & & & & & & & & \\
    \text { Cats } N(x) & 12 & 66 & 382 & 2201 & 12680 & 73041 & 420715 & 2423316 & 13968290 & 80399780 \\
    \hline
    \end{array}\)

37. This exercise is a follow-up to Exercise 26 which more thoroughly explores the population growth of Painesville, Ohio. According to Wikipedia, the population of Painesville, Ohio is given by \[\begin{aligned}
    &\begin{array}{|l|r|r|r|r|r|r|r|r|r|r|}
    \hline \text { Year } t & 1860 & 1870 & 1880 & 1890 & 1900 & 1910 & 1920 & 1930 & 1940 & 1950 \\
    \hline \text { Population } & 2649 & 3728 & 3841 & 4755 & 5024 & 5501 & 7272 & 10944 & 12235 & 14432 \\
    \hline
    \end{array}\\
    &\begin{array}{|l|r|r|r|r|r|}
    \hline \text { Year } t & 1960 & 1970 & 1980 & 1990 & 2000 \\
    \hline \text { Population } & 16116 & 16536 & 16351 & 15699 & 17503 \\
    \hline
    \end{array}
    \end{aligned}\nonumber\]
    1. Use a graphing utility to perform an exponential regression on the data from 1860 through 1920 only, letting \(t = 0\) represent the year 1860 as before. How does this calculator model compare with the model you found in Exercise 26? Use the calculator’s exponential model to predict the population in 2010. (The 2010 census gave the population as 19,563)
    2. The logistic model fit to all of the given data points for the population of Painesville \(t\) years after 1860 (again, using \(t = 0\) as 1860) is \[P(t) = \dfrac{18691}{1+9.8505e^{-0.03617t}}\nonumber\] According to this model, what should the population of Painesville have been in 2010? (The 2010 census gave the population as 19,563.) What is the population limit of Painesville?
38. According to OhioBiz , the census data for Lake County, Ohio is as follows: \[\begin{aligned}
    &\begin{array}{|l|r|r|r|r|r|r|r|r|r|r|}
    \hline \text { Year } t & 1860 & 1870 & 1880 & 1890 & 1900 & 1910 & 1920 & 1930 & 1940 & 1950 \\
    \hline \text { Population } & 15576 & 15935 & 16326 & 18235 & 21680 & 22927 & 28667 & 41674 & 50020 & 75979 \\
    \hline
    \end{array}\\
    &\begin{array}{|l|r|r|r|r|r|}
    \hline \text { Year } t & 1960 & 1970 & 1980 & 1990 & 2000 \\
    \hline \text { Population } & 148700 & 197200 & 212801 & 215499 & 227511 \\
    \hline
    \end{array}
    \end{aligned}\nonumber\]
    1. Use your calculator to fit a logistic model to these data, using \(x = 0\) to represent the year 1860.
    2. Graph these data and your logistic function on your calculator to judge the reasonableness of the fit.
    3. Use this model to estimate the population of Lake County in 2010. (The 2010 census gave the population to be 230,041.)
    4. According to your model, what is the population limit of Lake County, Ohio?
39. According to Facebook , the number of active users of Facebook has grown significantly since its initial launch from a Harvard dorm room in February 2004. The chart below has the approximate number \(U(x)\) of active users, in , \(x\) months after February 2004. For example, the first entry \((10, 1)\) means that there were \(1\) million active users in December 2004 and the last entry \((77, 500)\) means that there were \(500\) million active users in July 2010.

    With the help of your classmates, find a model for this data.

40. Each Monday during the registration period before the Fall Semester at LCCC, the Enrollment Planning Council gets a report prepared by the data analysts in Institutional Effectiveness and Planning. While the ongoing enrollment data is analyzed in many different ways, we shall focus only on the overall headcount. Below is a chart of the enrollment data for Fall Semester 2008. It starts 21 weeks before “Opening Day” and ends on “Day 15” of the semester, but we have relabeled the top row to be \(x = 1\) through \(x = 24\) so that the math is easier. (Thus, \(x = 22\) is Opening Day.) \[\begin{aligned}
    &\begin{array}{|l|r|r|r|r|r|r|r|r|}
    \hline \text { Week } x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
    \hline \text { Total } & & & & & & & & \\
    \text { Headcount } & 1194 & 1564 & 2001 & 2475 & 2802 & 3141 & 3527 & 3790 \\
    \hline
    \end{array}\\
    &\begin{array}{|l|r|r|r|r|r|r|r|r|}
    \hline \text { Week } x & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\
    \hline \text { Total } & & & & & & & & \\
    \text { Headcount } & 4065 & 4371 & 4611 & 4945 & 5300 & 5657 & 6056 & 6478 \\
    \hline
    \end{array}
    \end{aligned}\nonumber\] \[\begin{array}{|l|r|r|r|r|r|r|r|r|}
    \hline \text { Week } x & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 \\
    \hline \text { Total } & & & & & & & & \\
    \text { Headcount } & 7161 & 7772 & 8505 & 9256 & 10201 & 10743 & 11102 & 11181 \\
    \hline
    \end{array}\nonumber\]

    With the help of your classmates, find a model for this data. Unlike most of the phenomena we have studied in this section, there is no single differential equation which governs the enrollment growth. Thus there is no scientific reason to rely on a logistic function even though the data plot may lead us to that model. What are some factors which influence enrollment at a community college and how can you take those into account mathematically?

41. When we wrote this exercise, the Enrollment Planning Report for Fall Semester 2009 had only 10 data points for the first 10 weeks of the registration period. Those numbers are given below. \[\begin{array}{|l|r|r|r|r|r|r|r|r|}
    \hline \text { Week } x & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 \\
    \hline \text { Total } & & & & & & & & \\
    \text { Headcount } & 7161 & 7772 & 8505 & 9256 & 10201 & 10743 & 11102 & 11181 \\
    \hline
    \end{array}\nonumber\]

    With the help of your classmates, find a model for this data and make a prediction for the Opening Day enrollment as well as the Day 15 enrollment. (WARNING: The registration period for 2009 was one week shorter than it was in 2008 so Opening Day would be \(x = 21\) and Day 15 is \(x = 23\).)

Answers

1. • \(A(t) = 500\left(1 + \frac{0.0075}{12}\right)^{12t}\)
   • \(A(5) \approx \$ 519.10\), \(A(10) \approx \$ 538.93\), \(A(30) \approx \$ 626.12\), \(A(35) \approx \$ 650.03\)
   • It will take approximately \(92\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(3.88\). This means that the investment is growing at an average rate of \(\$3.88\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(4.85\). This means that the investment is growing at an average rate of \(\$4.85\) per year at this point.
2. • \(A(t) = 500e^{0.0075t}\)
   • \(A(5) \approx \$ 519.11\), \(A(10) \approx \$ 538.94\), \(A(30) \approx \$ 626.16\), \(A(35) \approx \$ 650.09\)
   • It will take approximately \(92\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(3.88\). This means that the investment is growing at an average rate of \(\$3.88\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(4.86\). This means that the investment is growing at an average rate of \(\$4.86\) per year at this point.
3. • \(A(t) = 1000\left(1 + \frac{0.0125}{12}\right)^{12t}\)
   • \(A(5) \approx \$ 1064.46\), \(A(10) \approx \$ 1133.07\), \(A(30) \approx \$ 1454.71\), \(A(35) \approx \$ 1548.48\)
   • It will take approximately \(55\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(13.22\). This means that the investment is growing at an average rate of \(\$13.22\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(19.23\). This means that the investment is growing at an average rate of \(\$19.23\) per year at this point.
4. • \(A(t) = 1000e^{0.0125t}\)
   • \(A(5) \approx \$ 1064.49\), \(A(10) \approx \$ 1133.15\), \(A(30) \approx \$ 1454.99\), \(A(35) \approx \$ 1548.83\)
   • It will take approximately \(55\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(13.22\). This means that the investment is growing at an average rate of \(\$13.22\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(19.24\). This means that the investment is growing at an average rate of \(\$19.24\) per year at this point.
5. • \(A(t) = 5000\left(1 + \frac{0.02125}{12}\right)^{12t}\)
   • \(A(5) \approx \$ 5559.98\), \(A(10) \approx \$ 6182.67\), \(A(30) \approx \$ 9453.40\), \(A(35) \approx \$ 10512.13\)
   • It will take approximately \(33\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(116.80\). This means that the investment is growing at an average rate of \(\$116.80\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(220.83\). This means that the investment is growing at an average rate of \(\$220.83\) per year at this point.
6. • \(A(t) = 5000e^{0.02125t}\)
   • \(A(5) \approx \$ 5560.50\), \(A(10) \approx \$ 6183.83\), \(A(30) \approx \$ 9458.73\), \(A(35) \approx \$ 10519.05\)
   • It will take approximately \(33\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(116.91\). This means that the investment is growing at an average rate of \(\$116.91\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(221.17\). This means that the investment is growing at an average rate of \(\$221.17\) per year at this point.

8. \(P = \frac{2000}{e^{0.0025 \cdot 3}} \approx \$ 1985.06\)
9. \(P = \frac{5000}{\left(1 + \frac{0.0225}{12}\right)^{12 \cdot 10}} \approx \$ 3993.42\)
10. 1. \(A(8) = 2000\left(1 + \frac{0.0025}{12}\right)^{12 \cdot 8} \approx \$2040.40\)
    2. \(t = \dfrac{\ln(2)}{12 \ln\left(1 + \frac{0.0025}{12}\right)} \approx 277.29\) years
    3. \(P = \dfrac{2000}{\left(1 + \frac{0.0025}{12}\right)^{36}} \approx \$1985.06\)
11. 1. \(A(8) = 2000\left(1 + \frac{0.0225}{12}\right)^{12 \cdot 8} \approx \$2394.03\)
    2. \(t = \dfrac{\ln(2)}{12 \ln\left(1 + \frac{0.0225}{12}\right)} \approx 30.83\) years
    3. \(P = \dfrac{2000}{\left(1 + \frac{0.0225}{12}\right)^{36}} \approx \$1869.57\)
    4. \(\left(1 + \frac{0.0225}{12}\right)^{12} \approx 1.0227\) so the APY is 2.27%
12. \(A(3) = 5000e^{0.299 \cdot 3} \approx \$12,226.18\), \(A(6) = 5000e^{0.299 \cdot 6} \approx \$30,067.29\)

14. • \(k = \frac{\ln(1/2)}{5.27} \approx -0.1315\)
    • \(A(t) = 50e^{-0.1315t}\)
    • \(t = \frac{\ln(0.1)}{-0.1315} \approx 17.51\) years.
15. • \(k = \frac{\ln(1/2)}{14} \approx -0.0495\)
    • \(A(t) = 2e^{-0.0495t}\)
    • \(t = \frac{\ln(0.1)}{-0.0495} \approx 46.52\) days.
16. • \(k = \frac{\ln(1/2)}{27.7} \approx -0.0250\)
    • \(A(t) = 75e^{-0.0250t}\)
    • \(t = \frac{\ln(0.1)}{-0.025} \approx 92.10\) days.
17. • \(k = \frac{\ln(1/2)}{432.7} \approx -0.0016\)
    • \(A(t) = 0.29e^{-0.0016t}\)
    • \(t = \frac{\ln(0.1)}{-0.0016} \approx 1439.11\) years.
18. • \(k = \frac{\ln(1/2)}{704} \approx -0.0010\)
    • \(A(t) = e^{-0.0010t}\)
    • \(t = \frac{\ln(0.1)}{-0.0010} \approx 2302.58\) million years, or \(2.30\) billion years.
19. \(t = \frac{\ln(0.1)}{k} = -\frac{\ln(10)}{k}\)
20. \(V(t) = 25e^{\ln\left(\frac{4}{5}\right)t} \approx 25e^{-0.22314355t}\)
21. 1. \(G(0) = 9743.77\) This means that the GDP of the US in 2000 was \(\$9743.77\) billion dollars.
    2. \(G(7) = 13963.24\) and \(G(10) = 16291.25\), so the model predicted a GDP of \(\$ 13,963.24\) billion in 2007 and \(\$ 16,291.25\) billion in 2010.
22. 1. \(D(0) = 15\), so the tumor was 15 millimeters in diameter when it was first detected.
    2. \(t = \frac{\ln(2)}{0.0277} \approx 25\) days.
23. 1. \(k = \frac{\ln(2)}{20} \approx 0.0346\)
    2. \(N(t) = 1000e^{0.0346 t}\)
    3. \(t = \frac{\ln(9)}{0.0346} \approx 63\) minutes
24. 1. \(k = \frac{1}{2}\frac{\ln(6)}{2.5} \approx 0.4377\)
    2. \(N(t) = 2.5e^{0.4377 t}\)
    3. \(t = \frac{\ln(2)}{0.4377} \approx 1.58\) hours
25. \(N_{0}=52, k=\frac{1}{3} \ln \left(\frac{118}{52}\right) \approx 0.2731, N(t)=52 e^{0.2731 t} \cdot N(6) \approx 268\).
26. \(N_{0}=2649, k=\frac{1}{60} \ln \left(\frac{7272}{2649}\right) \approx 0.0168, N(t)=2649 e^{0.0168 t} \cdot N(150) \approx 32923\), so the population of Painesville in 2010 based on this model would have been 32,923.
27. 1. \(P(0) = \frac{120}{4.167} \approx 29\). There are 29 Sasquatch in Bigfoot County in 2010.
    2. \(P(3) = \frac{120}{1+3.167e^{-0.05(3)}} \approx 32\) Sasquatch.
    3. \(t = 20 \ln(3.167) \approx 23\) years.
    4. As \(t \rightarrow \infty\), \(P(t) \rightarrow 120\). As time goes by, the Sasquatch Population in Bigfoot County will approach 120. Graphically, \(y = P(x)\) has a horizontal asymptote \(y=120\).
28. 1. \(A(t) = Ne^{-\left(\frac{\ln(2)}{5730}\right)t} \approx Ne^{-0.00012097t}\)
    2. \(A(20000) \approx 0.088978 \cdot N\) so about 8.9% remains
    3. \(t \approx \dfrac{\ln(.42)}{-0.00012097} \approx 7171\) years old
29. \(A(t) = 2.3e^{-0.0138629t}\)

31. 1. \(T(t) = 75 + 105e^{-0.005005t}\)
    2. The roast would have cooled to \(140^{\circ}\)F in about 95 minutes.
32. From the graph, it appears that as \(x \rightarrow 0^{+}\), \(y \rightarrow \infty\). This is due to the presence of the \(\ln(x)\) term in the function. This means that Fritzy will never catch Chewbacca, which makes sense since Chewbacca has a head start and Fritzy only runs as fast as he does.

    

33. The steady state current is 2 amps.

36. The linear regression on the data below is \(y = 1.74899x + 0.70739\) with \(r^{2} \approx 0.999995\). This is an excellent fit. \[\begin{array}{|l|r|r|r|r|r|r|r|r|r|r|}
    \hline x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
    \hline \ln (N(x)) & 2.4849 & 4.1897 & 5.9454 & 7.6967 & 9.4478 & 11.1988 & 12.9497 & 14.7006 & 16.4523 & 18.2025 \\
    \hline
    \end{array}\nonumber\]

    \(N(x) = 2.02869(5.74879)^{x} = 2.02869e^{1.74899x}\) with \(r^{2} \approx 0.999995\). This is also an excellent fit and corresponds to our linearized model because \(\ln(2.02869) \approx 0.70739\).

37. 1. The calculator gives: \(y = 2895.06 (1.0147)^{x}\). Graphing this along with our answer from Exercise 26 over the interval \([0,60]\) shows that they are pretty close. From this model, \(y(150) \approx 25840\) which once again overshoots the actual data value.
    2. \(P(150) \approx 18717\), so this model predicts 17,914 people in Painesville in 2010, a more conservative number than was recorded in the 2010 census. As \(t \rightarrow \infty\), \(P(t) \rightarrow 18691\). So the limiting population of Painesville based on this model is 18,691 people.
38. 1. \(y = \dfrac{242526}{1+874.62e^{-0.07113x}}\), where \(x\) is the number of years since 1860.
    2. The plot of the data and the curve is below.

       

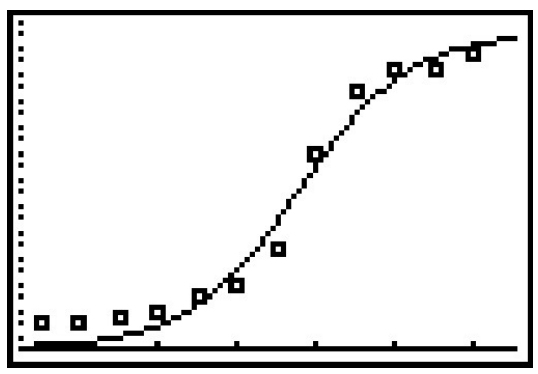
    3. \(y(140) \approx 232889\), so this model predicts 232,889 people in Lake County in 2010.
    4. As \(x \rightarrow \infty\), \(y \rightarrow 242526\), so the limiting population of Lake County based on this model is 242,526 people.