10.7: Trigonometric Equations and Inequalities

Solving "Basic" Trigonometric Equations

In Sections 10.2, 10.3, and most recently 10.6, we solved some basic equations involving trigonometric functions. In this section, we expand our skill set to handle a broader variety of equations involving trigonometric functions. The base tactic employs two critical elements from Trigonometry - reference angles and quadrants.¹

Strategy for Solving "Basic" Trigonometric Equations

Given any trigonometric equation of the form \[ \text{trig}(u) = c, \label{trigeqn}\]where "trig" could be \( \sin, \cos, \tan, \csc, \sec, \) or \( \cot \), do the following:

1. If the value of \( c \) is such that \( u \) is an axial angle, skip to Step 5.
2. Find the reference angle, \( \hat{u} \).
3. Use the sign of \( c \) to determine in which quadrants \( u \) terminates.
4. Using the reference angle from Step 2, write the solutions associated with the quadrants listed in Step 3. If possible, compress the solution set to a single equation (this is most often the case with equations involving the tangent or the cotangent).
5. If \( u \) is a function of another variable, solve the equations in Step 4 (or Step 1, if the angle is an axial angle) for the "true" variable.
6. Check for extraneous solutions!

A few notes about this strategy are in order and I will focus on showcasing how to solve \( \cos(3x) = \frac{\sqrt{3}}{2} \) while making my remarks.

First, I am using the variable \( u \) for the argument of the trigonometric function instead of the traditional "angular" variables \( t \), \( \alpha \), \( \beta \), \( \theta \), or \( x \). This is purposeful because, given a more complex trigonometric equation, we will often need to perform a \( u \)-substitution to get the equation into a more "basic" form. For example, given \( \cos(3x) = \frac{\sqrt{3}}{2} \), we will perform a \( u \)-substitution by letting \( u = 3x \). This simplifies our equation to the more "basic" form, \[\cos\left(u \right) = \frac{\sqrt{3}}{2}.\nonumber\]

To determine the reference angle, \( \hat{u} \), needed so that \( \cos(\hat{u}) = \frac{\sqrt{3}}{2} \), we refer to our special triangles. In this case, we find \( \hat{u} = \frac{\pi}{6} \).

Second, since all trigonometric functions are positive in QI and one other quadrant, there will be two quadrants in which the angle \( u \) will terminate if \( c \gt 0 \). A similar argument shows that there will be two quadrants in which \( u \) terminates if \( c \lt 0 \). In our current example, \( \cos(u) \) is positive. Therefore, \( u \) will terminate in QI and QIV (the quadrants where cosine is positive).

Using the reference angle, \( \hat{u} = \frac{\pi}{6} \), we write the solutions associated with quadrants I and IV.\[ \begin{array}{lrclclcl}
\text{Solutions associated with QI: } & u & = & \hat{u} + 2\pi k & = & \frac{\pi}{6} + 2 \pi k & & \\
\text{Solutions associated with QIV: } & u & = & 2\pi - \hat{u} + 2\pi k & = & 2\pi - \frac{\pi}{6} + 2 \pi k & = & \frac{11\pi}{6} + 2 \pi k, \\
\end{array} \nonumber \]

where \( k \in \mathbb{Z} \). The addition of \( 2 \pi k \) represents the fact that any full rotation of \( 2\pi \) lands the terminating side of \( u \) at the same spot. I leave it to the reader to verify the given solutions do indeed terminate in QI and QIV.

Our task in the original equation was to solve for \( x \) - not \( u \). Substituting \( u = 3x \) into our solutions, we get\[ \begin{array}{lrcl}
\text{Solutions associated with QI: } & 3x & = & \frac{\pi}{6} + 2 \pi k & & \\
\text{Solutions associated with QIV: } & 3x & = & \frac{11\pi}{6} + 2 \pi k. \\
\end{array} \nonumber \]

Finally, dividing both sides of each equation by \( 3 \),² we arrive at our solutions.\[ \begin{array}{lrcl}
\text{Solutions associated with QI: } & x & = & \frac{\pi}{18} + \frac{2 \pi}{3} k & & \\
\text{Solutions associated with QIV: } & x & = & \frac{11\pi}{18} + \frac{2 \pi}{3} k. \\
\end{array} \nonumber \]

Notice that \( \frac{11 \pi}{18} \) does not terminate in QIV yet it is supposed to be associated with QIV. Did we do something wrong? This leads to my third note. In Step 4, I use the word "associated" because, as was mentioned previously, \( u \) is generally a substitution for a more complex variable expression. In our current example, we were originally given \( \cos(3x) = \frac{\sqrt{3}}{2} \). We let \( u = 3x \) and solved \( \cos(u) = \frac{\sqrt{3}}{2} \) to get \( u = \frac{\pi}{6} + 2 \pi k \) and \( u = \frac{11 \pi}{6} + 2 \pi k \). These angles occur in QI and QIV, respectively (where the cosine is positive). So far, we should feel good about our results; however, QI and QIV are the quadrants where \( u \) terminates - not \( x \). Since we are supposed to be solving for \( x \), it is often the case that the angular frequency (the coefficient on \( x \)) will change the final quadrants of the solutions. This is absolutely fine!

For example, while \( x = \frac{11 \pi}{18} \in \text{QII} \neq \text{QIV} \), substituting this into our original equation, we get\[ \cos{\left( 3 \left( \frac{11 \pi}{18} \right) \right)} = \cos{\left( \frac{11 \pi}{6} \right)}. \nonumber \]Our final argument, \( \frac{11 \pi}{6} \), is actually an angle in QIV.

We will repeat this technique in the example below.

Example \( \PageIndex{1} \)

Solve the following equations and check your answers analytically. List the solutions which lie in the interval \([0,2\pi)\) and verify them analytically (i.e., by hand) or by using graphing technology.

1. \(\sin(2x) = -\frac{\sqrt{3}}{2}\)
2. \(\csc\left(\frac{1}{3}x-\pi \right) = \sqrt{2}\)
3. \(\cot\left(3x \right) = 0\)
4. \(\sec^{2}(x) = 4\)
5. \(\tan\left(\frac{x}{2}\right) = -3\)
6. \(\sin(2x) = 0.87\)

Solution

1. We begin by letting \( u = 2x \). We now need to solve\[\sin(u) =-\frac{\sqrt{3}}{2}.\nonumber\]This is a special ratio, so quickly drawing one of our special triangles we find that\[ \sin(\hat{u}) = \left| -\frac{\sqrt{3}}{2} \right| = \frac{\sqrt{3}}{2} \nonumber \]when \( \hat{u} = \frac{\pi}{3} \). Thus, our reference angle is \( \hat{u} = \frac{\pi}{3} \). Since \( \sin(u) \) is negative, we are concerned with solutions associated with QIII and QIV. \[ \begin{array}{lrclclcl}
   \text{Solutions associated with QIII: } & u & = & \pi + \hat{u} + 2\pi k & = & \pi + \frac{\pi}{3} + 2 \pi k & = & \frac{4 \pi}{3} + 2 \pi k \\
   \text{Solutions associated with QIV: } & u & = & 2\pi - \hat{u} + 2\pi k & = & 2\pi - \frac{\pi}{3} + 2 \pi k & = & \frac{5 \pi}{3} + 2 \pi k, \\
   \end{array} \nonumber \]for \( k \in \mathbb{Z} \). Resubstituting \( 2x = u \), we get\[ \begin{array}{lrcl}
   \text{Solutions associated with QIII: } & 2x & = & \frac{4 \pi}{3} + 2 \pi k \\
   \text{Solutions associated with QIV: } & 2x & = & \frac{5 \pi}{3} + 2 \pi k. \\
   \end{array} \nonumber \]Dividing both equations by \( 2 \), we arrive at\[ \begin{array}{lrcl}
   \text{Solutions associated with QIII: } & x & = & \frac{2 \pi}{3} + \pi k \\
   \text{Solutions associated with QIV: } & x & = & \frac{5 \pi}{6} + \pi k. \\
   \end{array} \nonumber \]To restrict the solutions to the interval \( [0, 2 \pi) \), we let \( k = 0 \) to find \( x = \frac{2 \pi}{3} \) and \( x = \frac{5 \pi}{6} \), both of which are in \( [0, 2 \pi) \). Trying \( k = 1 \), we get \( x = \frac{5 \pi}{3} \) and \( x = \frac{11 \pi}{6} \). Again, these angles are in the interval \( [0, 2 \pi) \). If we try letting \( k =  2 \), we quickly see that we will be adding \( 2 \pi \) to already positive angles which will result in angles outside the interval \( [0, 2 \pi) \). Thus, the solutions of the original equation on the interval \( [0, 2 \pi) \) are\[ x = \frac{2 \pi}{3}, \frac{5 \pi}{6}, \frac{5 \pi}{3}, \text{ and } \frac{11 \pi}{6}. \nonumber \]To check our solutions graphically, we use Desmos to graph \( y = \sin(2x) \) and \( y = -\frac{\sqrt{3}}{2} \) and look at their intersection points. It is important to note that graphically verifying answers is not the best approach as computers (and calculators) will often not give exact values of the intersection points.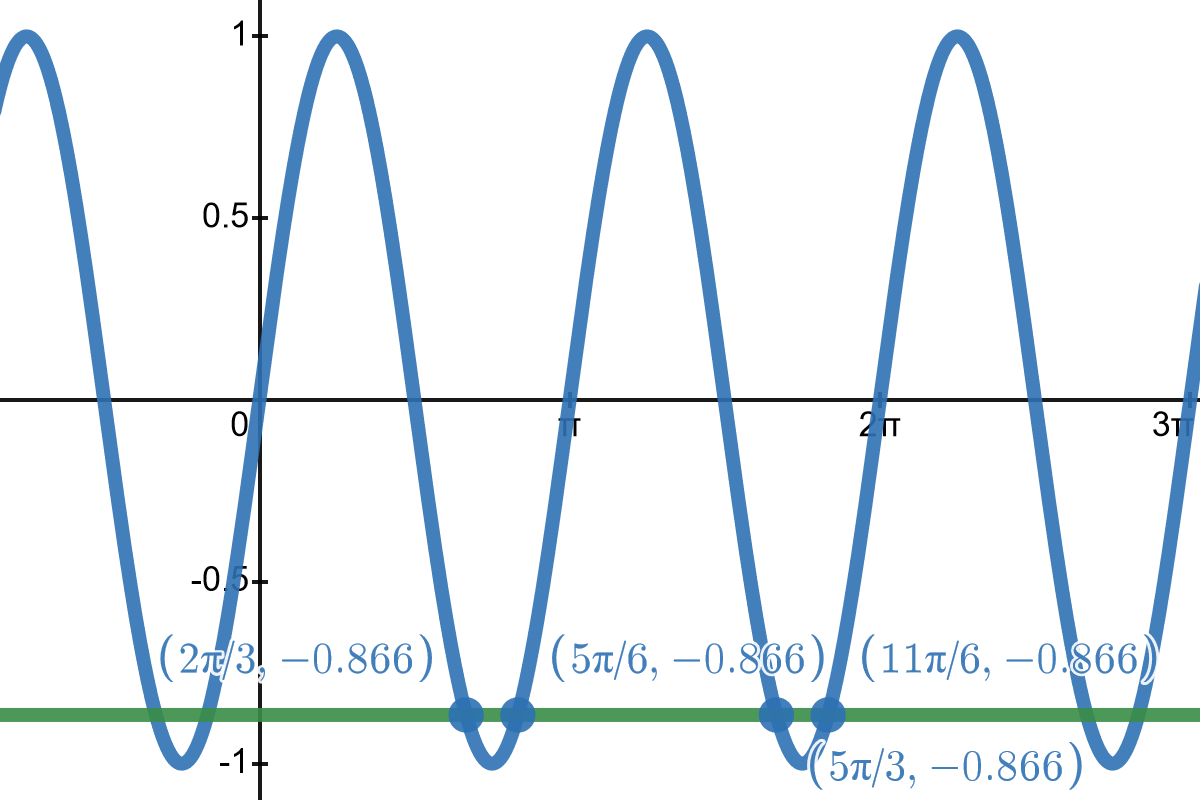

   

   ---

2. This looks like it might be more challenging than part 1, but that's an illusion. We begin by simplifying matters and let \( u = \frac{1}{3}x - \pi \). Our equation now has the form \[\csc(u) = \sqrt{2}.\nonumber\]\( \sqrt{2} = \frac{\sqrt{2}}{1} \) is a special ratio, and referring to our special triangles, we see that the cosecant of \( \frac{\pi}{4} \) is \( \sqrt{2} \). Therefore, our reference angle is \( \hat{u} = \frac{\pi}{4} \). Moreover, since \( \csc(u) \) is positive, we are going to limit our initial work to quadrants I and II (where the cosecant is positive). \[ \begin{array}{lrclclcl}
   \text{Solutions associated with QI: } & u & = & \hat{u} + 2\pi k & = & \frac{\pi}{4} + 2 \pi k & & \\
   \text{Solutions associated with QII: } & u & = & \pi - \hat{u} + 2\pi k & = & \pi - \frac{\pi}{4} + 2 \pi k & = & \frac{3 \pi}{4} + 2 \pi k, \\
   \end{array} \nonumber \]for \( k \in \mathbb{Z} \). Resubsituting in for \( u \), we get\[ \begin{array}{lrcl}
   \text{Solutions associated with QI: } & \frac{1}{3}x - \pi & = & \frac{\pi}{4} + 2 \pi k \\
   \text{Solutions associated with QII: } & \frac{1}{3}x - \pi & = & \frac{3 \pi}{4} + 2 \pi k. \\
   \end{array} \nonumber \]These are both just basic algebra problems. Adding \( \pi \) to both sides, we get\[ \begin{array}{lrcl}
   \text{Solutions associated with QI: } & \frac{1}{3}x & = & \frac{5 \pi}{4} + 2 \pi k \\
   \text{Solutions associated with QII: } & \frac{1}{3}x & = & \frac{7 \pi}{4} + 2 \pi k. \\
   \end{array} \nonumber \]A common error is to treat the "\(2\pi k\)" and "\(\pi\)" terms as "like" terms and try to combine them when they are not.³ Finally, we multiply both sides of each equation by \( 3 \), we get \[ \begin{array}{lrcl}
   \text{Solutions associated with QI: } & x & = & \frac{15 \pi}{4} + 6 \pi k \\
   \text{Solutions associated with QII: } & x & = & \frac{21 \pi}{4} + 6 \pi k. \\
   \end{array} \nonumber \]Let's check our work analytically. To check the first family of answers, we substitute, combine like terms, and simplify.\[\begin{array}{rclr}
   \csc\left(\frac{1}{3} \left[ \frac{15\pi}{4} + 6 \pi k \right] - \pi \right) & = & \csc\left(\frac{5\pi}{4} + 2\pi k - \pi \right) & \\
   & = & \csc\left(\frac{\pi}{4} + 2\pi k\right) & \\
   & = & \csc\left(\frac{\pi}{4}\right) & \left(\text{the period of cosecant is }2\pi \right) \\
   & = & \sqrt{2} & \\
   \end{array}\nonumber\]The family \(x= \frac{21\pi}{4} + 6 \pi k\) checks similarly. Despite having infinitely many solutions, we find that none of them lie in \([0,2\pi)\).

   ---

3. \(\cot(3x) = 0\) has the form \(\cot(u) = 0\), where \( u = 3x \). This means that \( u \) is an axial angle. Therefore, \[u = \frac{\pi}{2} + \pi k,\nonumber\]where \( k \in \mathbb{Z} \). So, in this case, \[3x = \frac{\pi}{2} + \pi k.\nonumber\]Solving for \(x\) yields \[x = \frac{\pi}{6} + \frac{\pi}{3} k.\nonumber\]Checking our answers analytically, we get\[\begin{array}{rclr}
   \cot\left(3\left[ \frac{\pi}{6} + \frac{\pi}{3} k\right]\right) & = & \cot\left(\frac{\pi}{2} + \pi k\right) & \\
   & = & \cot\left(\frac{\pi}{2}\right) & \left( \text{the period of cotangent is }\pi \right) \\
   & = & 0 & \\
   \end{array}\nonumber\]As \(k\) runs through the integers, we obtain six answers, corresponding to \(k=0\) through \(k=5\), which lie in \([0, 2\pi)\): \(x = \frac{\pi}{6}\), \(\frac{\pi}{2}\), \(\frac{5\pi}{6}\), \(\frac{7\pi}{6}\), \(\frac{3\pi}{2}\) and \(\frac{11\pi}{6}\). To confirm these graphically, we must be careful. On many calculators, there is no function button for cotangent. We choose to use the quotient identity \(\cot(3x) = \frac{\cos(3x)}{\sin(3x)}\).⁴ Graphing \(y = \frac{\cos(3x)}{\sin(3x)}\) and \(y = 0\) (the \(x\)-axis), we see that the \(x\)-coordinates of the intersection points approximately match our solutions.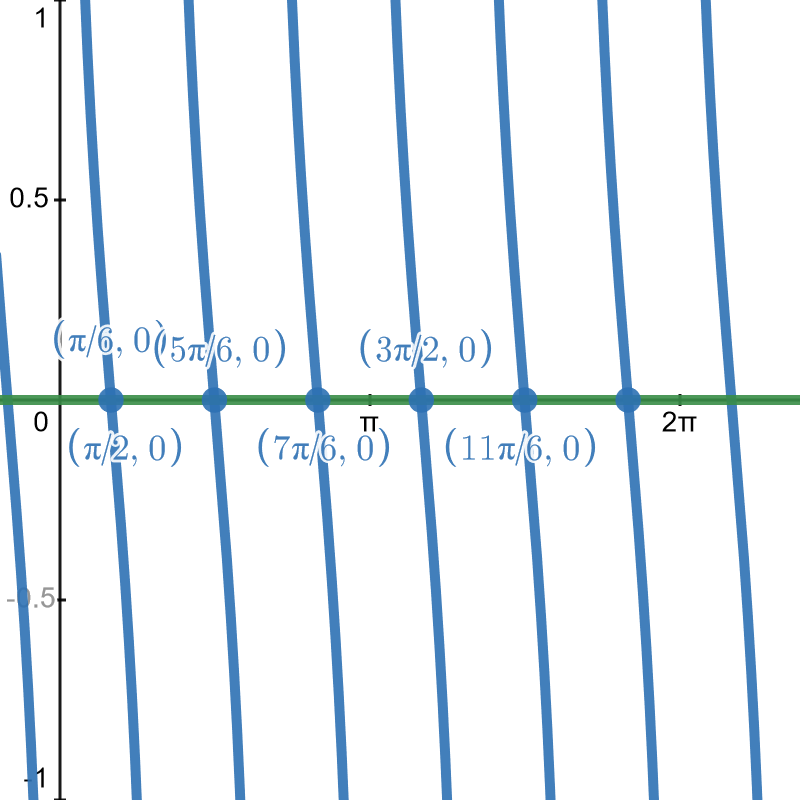

   

   ---

4. The complication in solving an equation like \(\sec^{2}(x) = 4\) comes not from the argument of secant, which is just \(x\), but rather, the fact the secant is being squared. We extract square roots to get \(\sec(x) = \pm 2\). Converting to cosines, we have \(\cos(x) = \pm \frac{1}{2}\). We know from our special triangles that \(  \hat{x} = \frac{\pi}{3} \). Furthermore, the fact that the cosine can be positive or negative means we are going to look at solutions in all quadrants.\[ \begin{array}{lrclclcl}
   \text{Solutions associated with QI: } & x & = & \hat{x} + 2\pi k & = & \frac{\pi}{3} + 2 \pi k & & \\
   \text{Solutions associated with QII: } & x & = & \pi - \hat{x} + 2\pi k & = & \pi - \frac{\pi}{3} + 2 \pi k & = & \frac{2 \pi}{3} + 2 \pi k \\
   \text{Solutions associated with QIII: } & x & = & \pi + \hat{x} + 2\pi k & = & \pi + \frac{\pi}{3} + 2 \pi k & = & \frac{4 \pi}{3} + 2 \pi k \\
   \text{Solutions associated with QIV: } & x & = & 2 \pi - \hat{x} + 2\pi k & = & 2 \pi - \frac{\pi}{3} + 2 \pi k & = & \frac{5 \pi}{3} + 2 \pi k \\
   \end{array} \nonumber \]for \( k \in \mathbb{Z} \). Writing our solutions this way is overkill. Notice that \( \frac{\pi}{3} \) and \( \frac{4 \pi}{3} \) differ by \( \pi \). The same can be said for \( \frac{2 \pi}{3} \) and \( \frac{5 \pi}{3} \). Hence, we can clean up our solutions as follows:\[ \begin{array}{lrcl}
   \text{Solutions associated with QI and QIII: } & x & = & \frac{\pi}{3} + \pi k \\
   \text{Solutions associated with QII and QIV: } & x & = & \frac{2 \pi}{3} + \pi k \\
   \end{array} \nonumber \]To check the first family of solutions, we note that, depending on the integer \(k\), \(\sec\left(\frac{\pi}{3} + \pi k\right)\) doesn’t always equal \(\sec\left(\frac{\pi}{3}\right)\). However, it is true that for all integers \(k\), \(\sec\left(\frac{\pi}{3} + \pi k\right) = \pm \sec\left(\frac{\pi}{3}\right) = \pm 2\). (Can you show this?) As a result,\[\begin{array}{rclr}
   \sec^{2}\left(\frac{\pi}{3} + \pi k\right) & = & \left( \pm \sec\left(\frac{\pi}{3}\right)\right)^2 & \\
   & = & (\pm 2)^2 & \\
   & = & 4 & \\
   \end{array}\nonumber\]The same holds for the family \(x =\frac{2\pi}{3} + \pi k\). The solutions which lie in \([0,2\pi)\) come from the values \(k = 0\) and \(k=1\), namely \(x = \frac{\pi}{3}\), \(\frac{2\pi}{3}\), \(\frac{4\pi}{3}\) and \(\frac{5\pi}{3}\). To confirm graphically, we use a reciprocal identity to rewrite the secant as cosine. The \(x\)-coordinates of the intersection points of \(y = \frac{1}{(\cos(x))^2}\) and \(y = 4\) verify our answers.

   

   ---

5. The equation \(\tan\left(\frac{x}{2}\right) = -3\) has the form \(\tan(u) = -3\), where \( u = \frac{x}{2} \). We have reached a case where the ratio in question is not from a special triangle nor does it represent the result of \( u \) being an axial angle. How do we proceed? If \( \hat{u} \) is the reference angle, then \( \tan(\hat{u}) = |-3| = 3 \).⁵ Therefore, \[\hat{u} = \arctan(3).\nonumber\]Since \( \tan(u) \) is negative, we will restrict our search for solutions to quadrants II and IV (where the tangent is negative). \[ \begin{array}{lrclcl}
   \text{Solutions associated with QII: } & u & = & \pi - \hat{u} + 2\pi k & = & \pi - \arctan(3) + \pi k \\
   \text{Solutions associated with QIV: } & u & = & 2 \pi - \hat{u} + 2\pi k & = & 2 \pi - \arctan(3) + \pi k, \\
   \end{array} \nonumber \]for \( k \in \mathbb{Z} \). Notice that we added \( \pi k \) instead of \( 2 \pi k \). This is because the tangent function (and the cotangent function, for that matter) repeat their behavior every \( \pi \) radians. Looking closely at these solutions, we can see that writing both is a bit overkill because when \( k = 1 \), the first solution becomes identical to the second solution at \( k = 0 \). Hence, we compress the equations into\[ \begin{array}{lrclcl}
   \text{Solutions associated with QII and QIV: } & u & = & \pi - \arctan(3) + \pi k. \\
   \end{array} \nonumber \]An oddity occurs here that represents our need to not fall asleep at the proverbial mathematical wheel. The terms \( \pi \) and \(  \pi k\) can be grouped to become \( \pi + \pi k = \pi (1 + k) \). Since \( k \) is any integer, we can replace \( 1 + k \) with \( j \), where \( j \in \mathbb{Z} \). Hence, \[ \begin{array}{lrclcl}
   \text{Solutions associated with QII and QIV: } & u & = & - \arctan(3) + \pi j, \\
   \end{array} \nonumber \]where \( j \in \mathbb{Z} \). Resubstituting \( \frac{x}{2} = u \), we get\[ \begin{array}{lrclcl}
   \text{Solutions associated with QII and QIV: } & \frac{x}{2} & = & - \arctan(3) + \pi j. \\
   \end{array} \nonumber \]Multiplying both sides of this equation by \( 2 \), we finally arrive at\[ \begin{array}{lrclcl}
   \text{Solutions associated with QII and QIV: } & x & = & - 2\arctan(3) + 2\pi j. \\
   \end{array} \nonumber \]To check our solutions, we note \[\begin{array}{rclr}
   \tan\left(\frac{-2\arctan(3) + 2\pi j}{2}\right) & = & \tan\left( -\arctan(3) + \pi j \right) & \\
   & = & \tan\left(-\arctan(3) \right) & (\text{the period of tangent is }\pi) \\
   & = & -\tan\left(\arctan(3) \right) & (\text{Even/Odd Identities}) \\
   & = & -3 & (\text{See Theorem 10.6.2}) \\
   \end{array}\nonumber\]To determine which of our answers lie in the interval \([0,2\pi)\), we first need to get an idea of the value of \(-2\arctan(3)\). While we could easily find an approximation using a calculator,⁶ we proceed analytically. Since \(3 \gt 0\), it follows that \[0 \lt \arctan(3) \lt \frac{\pi}{2}.\nonumber\]Multiplying through by \(-2\) gives \[0 \gt -2\arctan(3) \gt -\pi.\nonumber\]We are now in a position to argue which of the solutions \(x = -2\arctan(3) + 2\pi j\) lie in \([0,2\pi)\). For \(j = 0\), we get \(x = -2\arctan(3) \lt 0\), so we discard this answer and all answers \(x = -2\arctan(3) + 2\pi j\) where \(j \lt 0\). Next, we turn our attention to \(j = 1\) and get \(x = -2\arctan(3) + 2\pi\). Starting with the inequality \(-\pi \lt -2\arctan(3) \lt 0\), we add \(2\pi\) and get \(\pi < -2\arctan(3) +2\pi < 2\pi\). This means \(x = -2\arctan(3) + 2\pi\) lies in \([0,2\pi)\). Advancing \(j\) to \(2\) produces \(x = -2\arctan(3) + 4\pi\). Once again, we get from \(-\pi < -2\arctan(3) < 0\) that \(3\pi < -2\arctan(3) + 4\pi < 4\pi\). Since this is outside the interval \([0,2\pi)\), we discard \(x = -2\arctan(3) + 4\pi\) and all solutions of the form \(x = -2\arctan(3) + 2\pi j\) for \(j > 2\). Graphically, we see \(y = \tan\left(\frac{x}{2}\right)\) and \(y = -3\) intersect only once on \([0,2\pi)\) at \(x = -2\arctan(3) + 2\pi\approx 3.7851\).

   ---

6. We start, as usual, by letting \( u = 2x \). To solve \(\sin(u) = 0.87\), we note that the reference angle is \( \hat{u} = \arcsin(0.87) \) and, since \( \sin(u) \) is positive, we restrict our search to QI and QII. \[ \begin{array}{lrclclcl}
   \text{Solutions associated with QI: } & u & = & \hat{u} + 2\pi k & = & \arcsin(0.87) + 2 \pi k & & \\
   \text{Solutions associated with QII: } & u & = & \pi - \hat{u} + 2\pi k & = & \pi - \arcsin(0.87) + 2 \pi k & = & -\arcsin(0.87) + \pi (2 k + 1), \\
   \end{array} \nonumber \]where \( k \in \mathbb{Z} \). Again, keeping ourselves mentally sharp, we notice that \( 2 k \) is always even (if \( k \) is an integer). Therefore, \( 2k + 1 \) is always odd. Resubstituting \( 2x = u \), we get\[ \begin{array}{lrcl}
   \text{Solutions associated with QI: } & 2x & = & \arcsin(0.87) + 2 \pi k \\
   \text{Solutions associated with QII: } & 2x & = & -\arcsin(0.87) + \pi (2 k + 1). \\
   \end{array} \nonumber \]Dividing both sides of each equation by \( 2 \), we arrive at\[ \begin{array}{lrcl}
   \text{Solutions associated with QI: } & x & = & \frac{1}{2}\arcsin(0.87) + \pi k \\
   \text{Solutions associated with QII: } & 2x & = & -\frac{1}{2} \arcsin(0.87) + \frac{2 k + 1}{2} \pi. \\
   \end{array} \nonumber \]To check the first solution, \[\begin{array}{rclr}
   \sin\left(2\left[\frac{1}{2} \arcsin(0.87) + \pi k\right]\right) & = & \sin\left(\arcsin(0.87) + 2\pi k\right) & \\
    & = & \sin\left(\arcsin(0.87)\right) & \left( \text{the period of sine is }2\pi \right) \\
    & = & 0.87& (\text{See Theorem 10.6.1}) \\
   \end{array}\nonumber\]For the second solution, we get \[\begin{array}{rclr}
   \sin\left(2\left[- \frac{1}{2} \arcsin(0.87) + \frac{2k + 1}{2} \pi \right]\right) & = & \sin\left(- \arcsin(0.87) + (2k + 1)\pi \right) & \\
   & = & \sin\left(- \arcsin(0.87) + \pi + 2 \pi k \right) & \\
   & = & \sin\left(\pi - \arcsin(0.87)\right) & (\text{the period of sine is }2 \pi) \\
   & = & \sin\left(\arcsin(0.87)\right) & (\sin(\pi - t) = \sin(t)) \\
   & = & 0.87& (\text{See Theorem 10.6.1}) \\
   \end{array}\nonumber\]To determine which of these solutions lie in \([0,2\pi)\), we first need to get an idea of the value of \(x=\frac{1}{2} \arcsin(0.87)\) (where \( k = 0 \). Once again, we could use the calculator, but we adopt an analytic route here. By definition, \(0 < \arcsin(0.87) < \frac{\pi}{2}\) so that multiplying through by \(\frac{1}{2}\) gives us \(0 < \frac{1}{2} \arcsin(0.87) < \frac{\pi}{4}\). Starting with the family of solutions \(x = \frac{1}{2} \arcsin(0.87) + \pi k\), we use the same kind of arguments as in our solution to number 5 above and find only the solutions corresponding to \(k =0\) and \(k=1\) lie in \([0,2\pi)\): \(x = \frac{1}{2} \arcsin(0.87)\) and \(x = \frac{1}{2} \arcsin(0.87) + \pi\).
   Next, we move to the family \(x = -\frac{1}{2}\arcsin(0.87) + \frac{2k + 1}{2} \pi\) for integers \(k\). Again, starting with \( k = 0 \), we need to get a better estimate of \(\frac{\pi}{2} - \frac{1}{2} \arcsin(0.87)\). From the inequality \(0 < \frac{1}{2}\arcsin(0.87) < \frac{\pi}{4}\), we first multiply through by \(-1\) and then add \(\frac{\pi}{2}\) to get \(\frac{\pi}{2} > \frac{\pi}{2} -\frac{1}{2} \arcsin(0.87) > \frac{\pi}{4}\), or \(\frac{\pi}{4} < \frac{\pi}{2} -\frac{1}{2} \arcsin(0.87) < \frac{\pi}{2}\). Proceeding with the usual arguments, we find the only solutions which lie in \([0,2\pi)\) correspond to \(k = 0\) and \(k=1\), namely \(x =\frac{\pi}{2} - \frac{1}{2}\arcsin(0.87)\) and \(x = \frac{3\pi}{2} - \frac{1}{2}\arcsin(0.87)\). All told, we have found four solutions to \(\sin(2x) = 0.87\) in \([0,2\pi)\): \(x =\frac{1}{2} \arcsin(0.87)\), \(x=\frac{1}{2} \arcsin(0.87) + \pi\), \(x =\frac{\pi}{2} - \frac{1}{2}\arcsin(0.87)\) and \(x = \frac{3\pi}{2} - \frac{1}{2}\arcsin(0.87)\). By graphing \(y = \sin(2x)\) and \(y = 0.87\), we confirm our results.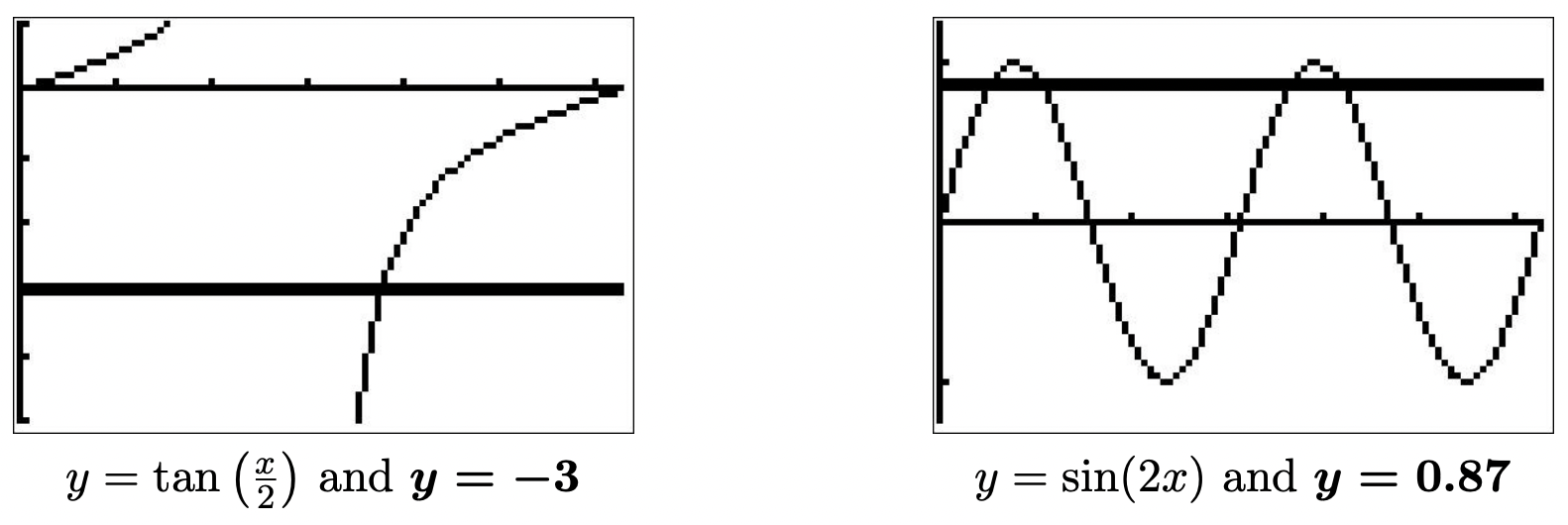

   

Subsection Footnotes

¹ As has already been mentioned, understanding how impactful reference angles and quadrants are in Trigonometry will allow you to easily master the subject.

² Don’t forget to divide \(2 \pi k\) by 3 as well!

³ Do you see why?

⁴ The reader is encouraged to see what happens if we had chosen the reciprocal identity \(\cot (3 x)=\frac{1}{\tan (3 x)}\) instead. The graph on the calculator appears identical, but what happens when you try to find the intersection points?

⁵ Reference angles are always between \( 0 \) and \( \frac{\pi}{2} \) radians (inclusive). Therefore, any trigonometric function evaluated at a reference angle will be positive!

⁶ Your instructor will let you know if you should abandon the analytic route at this point and use your calculator. But seriously, what fun would that be?

---

Solving Equations Involving Different Trigonometric Functions Having the Same Angular Frequencies

Each of the problems in Example \( \PageIndex{1} \) was ideal in that it featured one trigonometric function. If, for example, we were faced with solving \[\sec^{2}(x) = \tan(x) + 3,\nonumber\]what would we do? If our ultimate goal is to refine a given trigonometric equation to the form of Equation \( \ref{trigeqn} \), how can we do this if the equation involves different trigonometric functions?

The answer to these questions comes from a mixture of trigonometric identities and algebraic manipulations. In this section, we see (via example) that, given an equation involving two different trigonometric functions with the same angular frequency,⁷ we will need to use trigonometric identities and Algebra to simplify the equation to a form involving either a single trigonometric function or the product of different trigonometric functions equaling zero.

Example \( \PageIndex{2} \)

Solve the following equations and list the solutions which lie in the interval \([0,2\pi)\) and verify them analytically (i.e., by hand) or by using graphing technology.

1. \(3\cos(x) \sin^{2}(x) = \sin^{2}(x)\)
2. \(\sec^{2}(x) = \tan(x) + 3\)

Solution

1. We resist the temptation to divide both sides of \(3\cos(x)\sin^{2}(x) = \sin^{2}(x)\) by \(\sin^{2}(x)\) (recall, we have stated repeatedly that dividing by a variable expression implies you are assuming the expression is nonzero, which might not be the case) and instead gather all of the terms to one side of the equation and factor.\[\begin{array}{rclr}
   3\cos(x) \sin^{2}(x) & = & \sin^{2}(x) & \\
   3\cos(x) \sin^{2}(x) - \sin^{2}(x) & = & 0 & \\
   \sin^{2}(x) (3 \cos(x) - 1) & = & 0 & \left( \text{Factor out }\sin^{2}(x)\text{ from both terms}\right) \\
   \end{array}\nonumber\]We get \[\sin^{2}(x) = 0 \qquad \text{or} \qquad 3\cos(x) - 1 = 0.\nonumber\]Solving each, we find \[\sin(x) = 0 \qquad \text{or} \qquad \cos(x) = \frac{1}{3}.\nonumber\]These equations are both of the form of Equation \( \ref{trigeqn} \) so solving them will not be too bad.
   The right side of \( \sin(x) = 0 \) implies an axial angle. The solution to this equation is \(x = \pi k\), with \(x = 0\) and \(x = \pi\) being the two solutions which lie in \([0,2\pi)\).
   To solve \(\cos(x) = \frac{1}{3}\), we note that the reference angle is \(\hat{x} = \arccos\left(\frac{1}{3}\right)\). Since the cosine is positive, we know that the quadrants in question are QI and QIV. Hence, the two families of solutions are \[ \begin{array}{lrclclcl}
   \text{Solutions associated with QI: } & x & = & \hat{x} + 2\pi k & = & \arccos\left(\frac{1}{3}\right) + 2 \pi k & & \\
   \text{Solutions associated with QIV: } & x & = & 2\pi - \hat{x} + 2\pi k & = & 2\pi - \arccos\left(\frac{1}{3}\right) + 2 \pi k & = & -\arccos\left(\frac{1}{3}\right) + 2 \pi j, \\
   \end{array} \nonumber \]where \( j, k \in \mathbb{Z} \). Note that I have, yet again, rewritten \( 2 \pi + 2 \pi k = 2 \pi ( 1 + k) = 2 \pi j\).
   We find the two solutions here which lie in \([0,2\pi)\) to be \(x = \arccos\left(\frac{1}{3}\right)\) and \(x = 2\pi - \arccos\left(\frac{1}{3}\right)\). We leave it to the reader to check these solutions graphically.
   Thus, the solutions to the original equation on the interval \( [0, 2 \pi) \) are \[ x = 0, \arccos\left(\frac{1}{3}\right), \pi, \text{ and } 2\pi - \arccos\left(\frac{1}{3}\right). \nonumber \]

   ---

2. The \( \sec^2(x) \) in an equation with \( \tan(x) \) screams "Pythagorean Identity!" \[\begin{array}{rclr}
   \sec^{2}(x) & = & \tan(x) + 3 & \\
   1 + \tan^{2}(x) & = & \tan(x) + 3 & \left( \text{Pythagorean Identity} \right) \\
   \tan^{2}(x) - \tan(x) -2 & = & 0 & \\
   u^2 - u - 2 & = & 0 & \left( u-\text{substitution} \right) \\
   (u + 1)(u - 2) & = & 0 & \\
   \end{array}\nonumber\]This gives \(u = -1\) or \(u = 2\). Since \(u = \tan(x)\), we have \(\tan(x) = -1\) or \(\tan(x) = 2\).
   Considering \(\tan(x) = -1\), we recognize the reference angle to be \( \frac{\pi}{4} \) and the quadrants to be QII and QIV.\[ \begin{array}{lrclclcl}
   \text{Solutions associated with QII and QIV: } & x & = & \pi - \hat{x} + \pi k & = & \pi - \frac{\pi}{4} + \pi k & = & - \frac{\pi}{4} + \pi j \\
   \end{array} \nonumber \]where \( j = k + 1 \) and \( k \in \mathbb{Z} \). Instead of checking these solutions immediately, let's restrict our potential solutions to the interval \( [0 , 2 \pi) \).⁸ For \( j = 0 \), we get \( x = -\frac{\pi}{4} \), which will not work. Moving on to \( j = 1 \) and \( j = 2 \), we get \( x = \frac{3 \pi}{4} \) and \( x = \frac{7 \pi}{4} \), respectively. Any further, and our values for \( x \) will go beyond the requested interval. 
   Checking these refined solutions, we get\[ \begin{array}{lrcl}
   \text{For }x = \frac{3 \pi}{4} & & & \\
   & \sec^2{\left( \frac{3 \pi}{4} \right)} & \overset{\text{?}}{=} & \tan{ \left( \frac{3 \pi}{4} \right) } + 3 \\
   \implies & \left( -\sqrt{2} \right)^2 & \overset{\text{?}}{=} & -1 + 3 \\
   \implies & 2 & \overset{\text{?}}{=} & 2 \\
   \end{array} \nonumber \]Thus, we can see \( x = \frac{3 \pi}{4} \) works.\[ \begin{array}{lrcl}
   \text{For }x = \frac{7 \pi}{4} & & & \\
   & \sec^2{\left( \frac{7 \pi}{4} \right)} & \overset{\text{?}}{=} & \tan{ \left( \frac{7 \pi}{4} \right) } + 3 \\
   \implies & \left( \sqrt{2} \right)^2 & \overset{\text{?}}{=} & -1 + 3 \\
   \implies & 2 & \overset{\text{?}}{=} & 2 \\
   \end{array} \nonumber \]We see that \( x = \frac{7 \pi}{4} \) works as well.
   Now we look at \(\tan(x) = 2\). We should immediately recognize the right-hand side is not a special ratio for the tangent function. Therefore, we set the reference angle to \( \hat{x} = \arctan(|2|) = \arctan(2) \). Since the tangent function is positive in this case, the quadrants of interest are QI and QIII.\[ \begin{array}{lrclcl}
   \text{Solutions associated with QI and QIII: } & x & = & \hat{x} + \pi k & = & \arctan(2) + \pi k \\
   \end{array} \nonumber \]where \( k \in \mathbb{Z} \). On \( \left[ 0, 2\pi \right) \), \( x = \arctan(2) \) and \( x = \arctan(2) + \pi \) are candidate solutions. Checking, we get\[ \begin{array}{lrcl}
   \text{For }x = \arctan(2) & & & \\
   & \sec^2{\left( \arctan(2) \right)} & \overset{\text{?}}{=} & \tan{ \left( \arctan(2) \right) } + 3 \\
   \end{array} \nonumber \]We need to reach back to Section 10.6 to help us with both the left- and right-hand sides of this equation. The right-hand side quickly simplifies to \( 2 + 3 = 5 \); however, the left-hand side requires us to let \( \hat{x} = \arctan(2) \implies \tan(\hat{x}) = 2 \). Luckily, \[ \sec^2{ \left( \arctan(2) \right) } = \sec^2{(\hat{x})} =  1 + \tan^2{(\hat{x})} = 1 + 2^2 = 5 \nonumber \]Therefore, the two sides are, in fact, equivalent.\[ \begin{array}{lrclr}
   \text{For }x = \arctan(2) + \pi & & & & \\
   & \sec^2{\left( \arctan(2) + \pi \right)} & \overset{\text{?}}{=} & \tan{ \left( \arctan(2) + \pi \right) } + 3 & \\
   \implies & 1 + \tan^2{\left( \arctan(2) + \pi \right)} & \overset{\text{?}}{=} & \tan{ \left( \arctan(2) \right) } + 3 & \left( \text{the period of tangent is }\pi \text{ and Pythagorean Identity} \right) \\
   \implies & 1 + \tan^2{\left( \arctan(2) \right) } & \overset{\text{?}}{=} & 5 & \left( \text{Reciprocal Identity and the period of tangent is }\pi \right) \\
   \implies & 1 + 2^2 & \overset{\text{?}}{=} & 5 &  \\
   \end{array} \nonumber \]Thus, \( x = \arctan(2) + \pi \) works as well. Hence, the solution set to the original equation on the interval \( \left[ 0, 2 \pi \right) \) is \[ x = \arctan(2), \frac{3 \pi}{4}, \arctan(2) + \pi, \text{ and } \frac{7 \pi}{4}. \nonumber \]

Subsection Footnotes

⁷ Recall from Section 10.5 that the angular frequency of a sinusoidal function is the coefficient of \( x \). That is, the angular frequency of \( f(x) = -2 \sin{(3x + 1)} - 4 \) is \( 3 \). In this section, we are slightly abusing the language "angular frequency" by allowing ourselves to include the non-sinusoidal trigonometric functions in this discussion.
⁸ I find it much better to get my "families of solutions" first, restrict them to the requested interval, then check solutions. It's a personal preference that, at times, can be inefficient; however, it avoids mistakes in the long run.

---

Solving Equations Involving Trigonometric Functions Having Different Angular Frequencies

If an equation contains more than one trigonometric function (whether the same or not) but with different angular frequencies, we will need to use the Double-Angle Identities (or, in rare cases, the Sum-to-Product or Product-to-Sum Formulas) and Algebra to simplify the equation to simpler equations of the form of Equation \( \ref{trigeqn} \).

Example \(\PageIndex{3}\)

Solve the following equations and list the solutions which lie in the interval \([0,2\pi)\). Verify your solutions on \([0,2\pi)\) graphically.

1. \(\cos(2x) = 3\cos(x) - 2\)
2. \(\cos(3x) = 2- \cos(x)\)
3. \(\cos(3x) = \cos(5x)\)
4. \(\sin(2x) =\sqrt{3} \cos(x)\)
5. \(\sin(x)\cos\left(\frac{x}{2}\right) + \cos(x)\sin\left(\frac{x}{2}\right) = 1\)

Solution

1. In the equation \(\cos(2x) = 3\cos(x) - 2\), we have the same circular function, namely cosine, on both sides but the arguments differ. Using the Double-Angle Identity \[\cos(2x) = 2\cos^{2}(x) - 1,\nonumber\]we obtain a "quadratic in disguise" and proceed as we have done in the past.\[\begin{array}{rclr}
   \cos(2x) & = & 3\cos(x) - 2 & \\
   2\cos^{2}(x) -1 & = & 3\cos(x) -2 & \left( \text{Double-Angle Identity} \right) \\
   2\cos^{2}(x) - 3\cos(x) +1 & = & 0 & \\
   2 u^2 - 3 u + 1 & = & 0 & \left( u-\text{Substitution} \right) \\
   (2u - 1)(u - 1) & = & 0 & \\
   \end{array}\nonumber\]This gives \(u = \frac{1}{2}\) or \(u = 1\). Since \(u = \cos(x)\), we get \(\cos(x) = \frac{1}{2}\) or \(\cos(x) = 1\).
   Solving \(\cos(x) = \frac{1}{2}\), we get \(\hat{x} = \frac{\pi}{3}\), and \( x \) is in QI or QIV.\[ \begin{array}{lrclclcl}
   \text{Solutions associated with QI: } & x & = & \hat{x} + 2\pi k & = & \frac{\pi}{3} + 2 \pi k & & \\
   \text{Solutions associated with QIV: } & x & = & 2\pi - \hat{x} + 2\pi k & = & 2\pi - \frac{\pi}{3} + 2 \pi k & = & \frac{5 \pi}{3} + 2 \pi k, \\
   \end{array} \nonumber \]where \( k \in \mathbb{Z} \).
   Solving \( \cos(x) = 1 \), we get \( x = 0 + 2 \pi k = 2 \pi k \).
   The answers which lie in \([0,2\pi)\) are \(x =0\), \(\frac{\pi}{3}\), and \(\frac{5\pi}{3}\). Graphing \(y = \cos(2x)\) and \(y = 3\cos(x) - 2\), we find, after a little extra effort, that the curves intersect in three places on \([0,2\pi)\), and the \(x\)-coordinates of these points confirm our results.

   ---

2. Most readers would stare at this problem in consternation; however, we have encountered something similar to this in the past. To solve \(\cos(3x) = 2- \cos(x)\), we need to get those angular frequencies to be the same. From Example 10.4.2, number 4, we know that \(\cos(3x) = 4\cos^{3}(x) - 3\cos(x)\). This transforms the equation into a polynomial in terms of \(\cos(x)\).\[\begin{array}{rrclr}
   & \cos(3x) & = & 2 - \cos(x) & \\
   \implies & 4\cos^{3}(x) - 3\cos(x) & = & 2- \cos(x) & \left( \text{Sum and Difference Identities to expand} \right) \\
   \implies & 2\cos^{3}(x) - 2\cos(x) -2 & = & 0 & \\
   \implies & 4 u^3 - 2 u -2 & = & 0 & \left( u-\text{Substition} \right) \\
   \end{array}\nonumber\]To solve \(4u^3-2u-2=0\), we need the techniques in Chapter 3 to factor \(4u^3-2u-2\) into \((u-1)\left(4u^2+4u+2\right)\). We get either \(u-1 = 0\) or \(4u^2+2u+2=0\), and since the discriminant of the latter is negative, the only real solution to \(4u^3-2u-2=0\) is \(u = 1\). Since \(u = \cos(x)\), we get \(\cos(x) = 1\), so \(x = 2\pi k\) for integers \(k\). The only solution which lies in \([0,2\pi)\) is \(x = 0\). Graphing \(y = \cos(3x)\) and \(y = 2- \cos(x)\) on the same set of axes over \([0,2\pi)\) shows that the graphs intersect at what appears to be \((0,1)\), as required.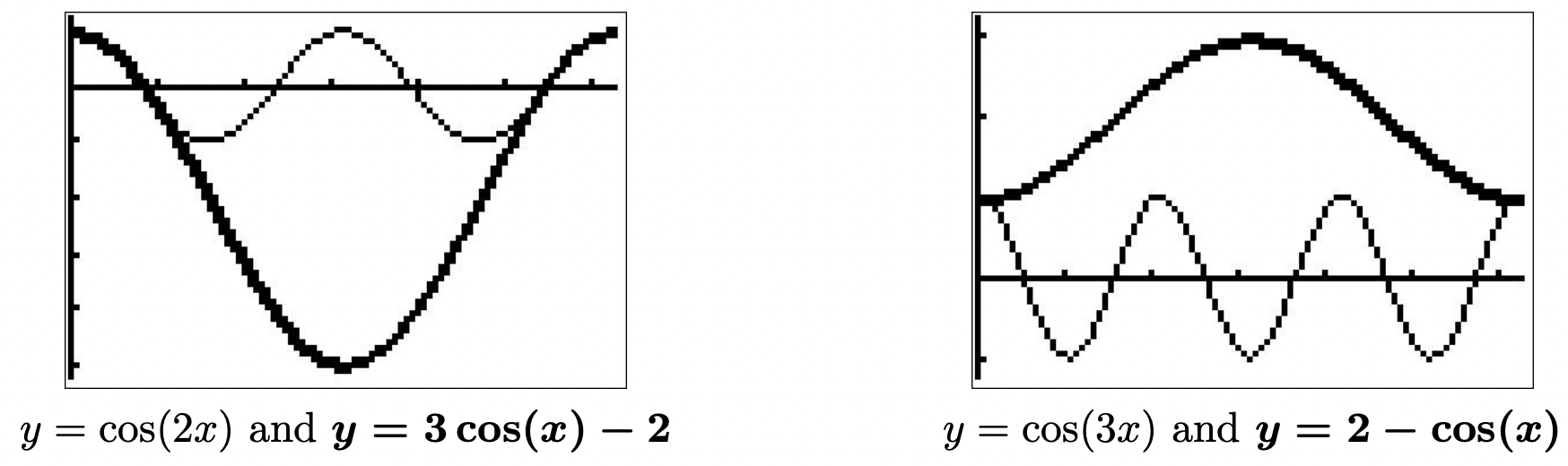

   

   ---

3. While we could approach \(\cos(3x) = \cos(5x)\) in the same manner as we did the previous problem, we choose instead to showcase the utility of the Sum-to-Product Formulas. From \(\cos(3x) = \cos(5x)\), we get \(\cos(5x) - \cos(3x) = 0\), and it is the presence of \(0\) on the right hand side that indicates a switch to a product would be a good move.⁹ Using the Sum-to-Product Formulas, we have that \[\cos(5x) - \cos(3x) = - 2 \sin\left( \frac{5x + 3x}{2}\right)\sin\left( \frac{5x - 3x}{2}\right) = -2 \sin(4x)\sin(x).\nonumber\]Hence, the equation \(\cos(5x) = \cos(3x)\) is equivalent to \(-2 \sin(4x) \sin(x) = 0\). From this, we get \(\sin(4x) = 0\) or \(\sin(x)\) = 0. Solving \(\sin(4x) = 0\) gives \(x = \frac{\pi}{4} k\) for integers \(k\) (notice how we are starting to speed up?), and the solution to \(\sin(x) = 0\) is \(x = \pi k\) for integers \(k\). The second set of solutions is contained in the first set of solutions,¹⁰ so our final solution to \(\cos(5x) = \cos(3x)\) is \(x = \frac{\pi}{4} k\) for integers \(k\). There are eight of these answers which lie in \([0,2\pi)\): \(x = 0\), \(\frac{\pi}{4}\), \(\frac{\pi}{2}\), \(\frac{3\pi}{4}\), \(\pi\), \(\frac{5\pi}{4}\), \(\frac{3\pi}{2}\) and \(\frac{7\pi}{4}\). Our plot of the graphs of \(y = \cos(3x)\) and \(y = \cos(5x)\) below (after some careful zooming) bears this out.

   ---

4. In examining the equation \(\sin(2x) =\sqrt{3} \cos(x)\), not only do we have different angular frequencies, we also have different circular functions to contend with. Using the identity \(\sin(2x) = 2 \sin(x) \cos(x)\) makes all of the arguments the same and we proceed as we would solving any nonlinear equation – gather all of the nonzero terms on one side of the equation and factor.\[\begin{array}{rclr}
   \sin(2x) & = & \sqrt{3} \cos(x) & \\
   2 \sin(x) \cos(x) & = & \sqrt{3} \cos(x) & \left( \text{Double-Angle Identity} \right) \\
   2\sin(x) \cos(x) - \sqrt{3} \cos(x) & = & 0 & \\
   \cos(x) (2 \sin(x) - \sqrt{3}) & = & 0 & \\
   \end{array}\nonumber\]from which we get \(\cos(x) = 0\) or \(\sin(x) = \frac{\sqrt{3}}{2}\). From \(\cos(x) = 0\), we obtain \(x = \frac{\pi}{2} + \pi k\) for integers \(k\). From \(\sin(x) = \frac{\sqrt{3}}{2}\), we get \(x = \frac{\pi}{3} + 2\pi k\) or \(x = \frac{2\pi}{3} + 2\pi k\) for integers \(k\). The answers which lie in \([0,2\pi)\) are \(x = \frac{\pi}{2}\), \(\frac{3\pi}{2}\), \(\frac{\pi}{3}\) and \(\frac{2\pi}{3}\). We graph \(y = \sin(2x)\) and \(y = \sqrt{3} \cos(x)\) and, after some careful zooming, verify our answers.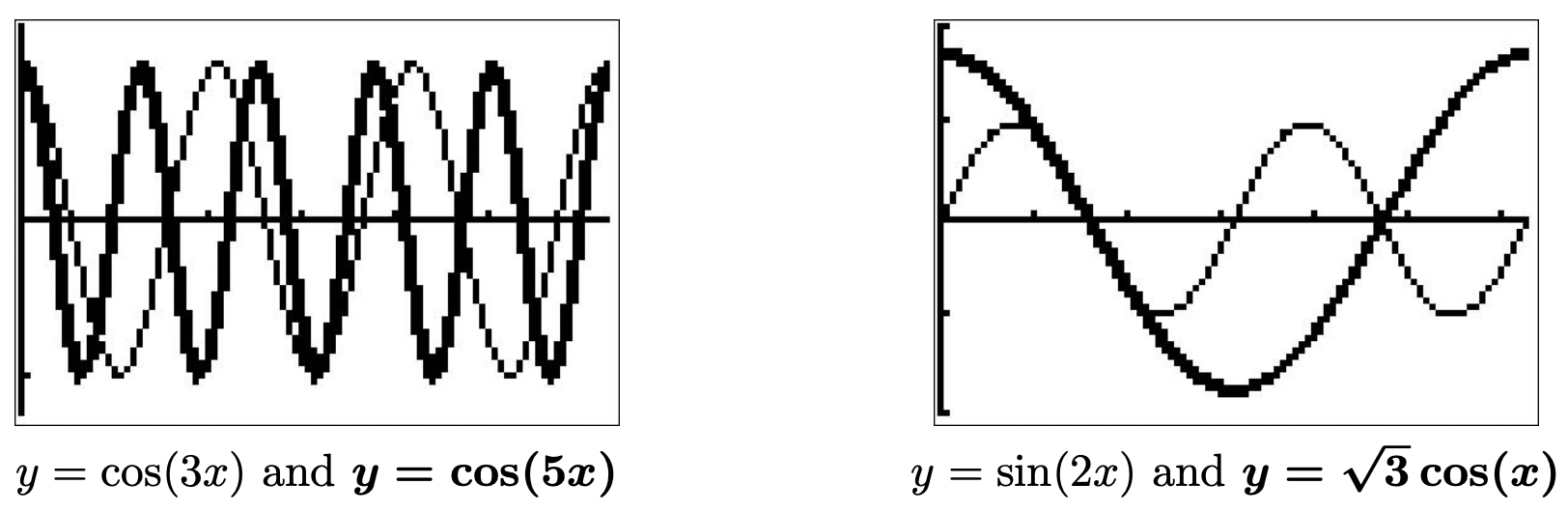

   

   ---

5. Unlike the previous problem, there seems to be no quick way to get the circular functions or their arguments to match in the equation \(\sin(x)\cos\left(\frac{x}{2}\right) + \cos(x)\sin\left(\frac{x}{2}\right) = 1\). If we stare at it long enough, however, we realize that the left-hand side is the expanded form of the Sum Identity for \(\sin\left(x + \frac{x}{2}\right)\). Hence, our original equation is equivalent to \(\sin\left(\frac{3}{2} x\right) = 1\). Solving, we find \(x = \frac{\pi}{3} + \frac{4\pi}{3} k\) for integers \(k\). Two of these solutions lie in \([0,2\pi)\): \(x = \frac{\pi}{3}\) and \(x = \frac{5\pi}{3}\). We leave it to the reader to verify the solution by graphing \(y = \sin(x)\cos\left(\frac{x}{2}\right) + \cos(x)\sin\left(\frac{x}{2}\right)\) and \(y = 1\).

Subsection Footnotes

⁹ As always, experience is the greatest teacher here!

¹⁰ As always, when in doubt, write it out!

---

Solving Other Trigonometric Equations

Just as we stated when solving systems of nonlinear equations in Section 9.3 - when it comes to solving equations involving the trigonometric functions, it helps to just try something. There is no way to cover all possible "oddball" cases, but the next example covers two styles that come up often enough.

Example \(\PageIndex{4}\)

Solve the equations and list the solutions which lie in the interval \([0,2\pi)\).

1. \(\cos(x) = \sin(x)\)
2. \(\cos(x) - \sqrt{3} \sin(x) = 2\)

Solution

1. This style of problem (along with the next one) often throws students off. The angular frequencies are the same, but the circular functions are different. This has not been an issue up to this point because all the previous examples involving two different circular functions had at least one of these functions being squared. Squares of trigonometric functions are blessings in disguise as we can always try to change them using the Pythagorean Identities. In this case, there are no squares. So what do we do? Since we would like squares, why don't we just square both sides?¹¹\[ \begin{array}{lrclr}
   & \cos(x) & = & \sin(x) & \\
   \implies & \cos^2(x) & = & \sin^2(x) & \left( \text{Square both sides} \right) \\
   \implies & 1 - \sin^2(x) & = & \sin^2(x) & \left( \text{Pythagorean Identity} \right) \\
   \implies & 1 & = & 2 \sin^2(x) &  \\
   \implies & \frac{1}{2} & = & \sin^2(x) &  \\
   \implies & \pm \frac{1}{\sqrt{2}} & = & \sin(x) &  \\
   \end{array} \nonumber \]Therefore, \( \hat{x} = \frac{\pi}{4} \) and we need to check all quadrants.\[ \begin{array}{lrclclcl}
   \text{Solutions associated with QI: } & x & = & \hat{x} + 2\pi k & = & \frac{\pi}{4} + 2 \pi k & & \\
   \text{Solutions associated with QII: } & x & = & \pi - \hat{x} + 2\pi k & = & \pi - \frac{\pi}{4} + 2 \pi k & = & \frac{3 \pi}{4} + 2 \pi k \\
   \text{Solutions associated with QIII: } & x & = & \pi + \hat{x} + 2\pi k & = & \pi + \frac{\pi}{4} + 2 \pi k & = & \frac{5 \pi}{4} + 2 \pi k \\
   \text{Solutions associated with QIV: } & x & = & 2\pi - \hat{x} + 2\pi k & = & 2\pi - \frac{\pi}{4} + 2 \pi k & = & \frac{7 \pi}{4} + 2 \pi k \\
   \end{array} \nonumber \]where \( k \in \mathbb{Z} \). This is a case where, rather than compressing these families of solutions into two families (which we could do), it's easier to just check the four possibilities separately. In all four cases, the reference angles are \( \hat{x} = \frac{\pi}{4} \). Therefore, the sine and cosine functions become \( \pm \frac{1}{\sqrt{2}} \). We just require the signs of these to be the same.
   In QI, \( \cos{\left( \frac{\pi}{4} \right)} = \frac{1}{\sqrt{2}} = \sin{\left( \frac{\pi}{4} \right)} \). In QII, \( \cos{\left( \frac{5\pi}{4} \right)} = -\frac{1}{\sqrt{2}} = \sin{\left( \frac{5\pi}{4} \right)} \); however, we can throw out the other two possibilities because the signs of the functions are opposite in both QII and QIV. Thus, the solution set on the interval \( \left[ 0, 2\pi \right) \) is \( x = \frac{\pi}{4} \text{ and } \frac{5 \pi}{4} \).

   ---

2. With the absence of double angles or squares, there doesn’t seem to be much we can do. However, since the arguments of the cosine and sine are the same, we can rewrite the left hand side of this equation as a sinusoid.¹² To fit \(f(x) = \cos(x) - \sqrt{3} \sin(x)\) to the form \(A\sin(B t + C) + D\), we use what we learned in Example 10.5.3 and find \(A = 2\), \(D = 0\), \(B = 1\) and \(C = \frac{5\pi}{6}\). Hence, we can rewrite the equation \(\cos(x) - \sqrt{3} \sin(x) = 2\) as \(2 \sin\left(x + \frac{5\pi}{6}\right) = 2\), or \(\sin\left(x + \frac{5\pi}{6}\right) = 1\). Solving the latter, we get \(x = - \frac{\pi}{3} + 2\pi k\) for integers \(k\). Only one of these solutions, \(x = \frac{5\pi}{3}\), which corresponds to \(k=1\), lies in \([0,2\pi)\).

Subsection Footnotes

¹¹ As you should recall from Algebra, when you square both sides of an equation, you run the risk of introducing extraneous solutions. Therefore, you must always check your solutions when you perform this action.

¹² We are essentially "undoing" the Sum and Difference Identity for cosine or sine, depending on which form we use, so this problem is actually closely related to Example \( \PageIndex{3} \) Part e!

---

Solving Trigonometric Inequalities

Next, we focus on solving inequalities involving the trigonometric functions. Since these functions are continuous on their domains, we may use the sign diagram technique we’ve used in the past to solve the inequalities.¹³

Example \( \PageIndex{5} \)

Solve the following inequalities on \([0,2\pi)\). Express your answers using interval notation and verify your answers graphically.

1. \(2\sin(x) \leq 1\)
2. \(\sin(2x) > \cos(x)\)
3. \(\tan(x) \geq 3\)

Solution

1. We begin solving \(2\sin(x) \leq 1\) by collecting all of the terms on one side of the equation and zero on the other to get \(2\sin(x) - 1 \leq 0\). Next, we let \(f(x) = 2\sin(x) - 1\) and note that our original inequality is equivalent to solving \(f(x) \leq 0\). We now look to see where, if ever, \(f\) is undefined and where \(f(x) = 0\). Since the domain of \(f\) is all real numbers, we can immediately set about finding the zeros of \(f\). Solving \(f(x) = 0\), we have \(2\sin(x) - 1=0\) or \(\sin(x) = \frac{1}{2}\). The solutions here are \(x = \frac{\pi}{6} + 2\pi k\) and \(x = \frac{5\pi}{6} + 2\pi k\) for integers \(k\). Since we are restricting our attention to \([0,2\pi)\), only \(x = \frac{\pi}{6}\) and \(x = \frac{5\pi}{6}\) are of concern to us. Next, we choose test values in \([0,2\pi)\) other than the zeros and determine if \(f\) is positive or negative there. For \(x = 0\) we have \(f(0) = -1\), for \(x = \frac{\pi}{2}\) we get \(f\left(\frac{\pi}{2}\right) = 1\) and for \(x = \pi\) we get \(f(\pi) = -1\). Since our original inequality is equivalent to \(f(x) \leq 0\), we are looking for where the function is negative \((-)\) or \(0\), and we get the intervals \(\left[0, \frac{\pi}{6}\right] \cup \left[\frac{5\pi}{6}, 2\pi \right)\). We can confirm our answer graphically by seeing where the graph of \(y = 2\sin(x)\) crosses or is below the graph of \(y = 1\).

   

   ---

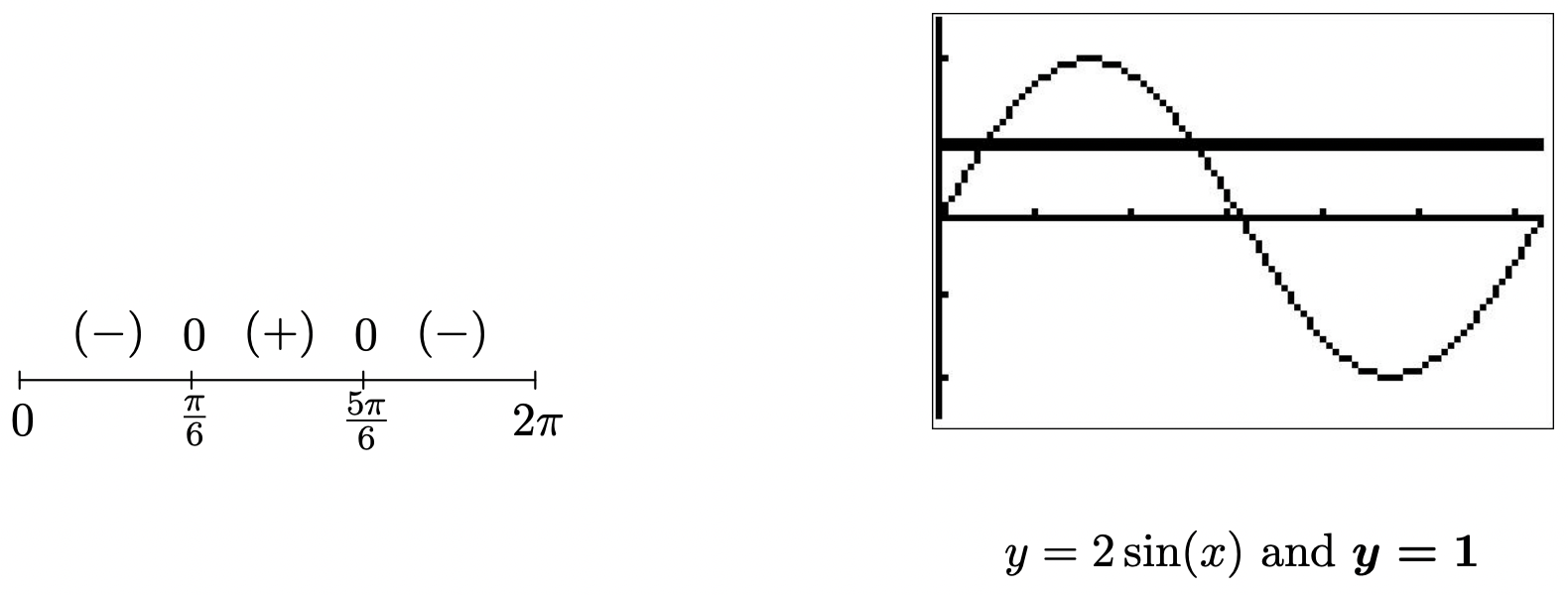
2. We first rewrite \(\sin(2x) > \cos(x)\) as \(\sin(2x) - \cos(x) > 0\) and let \(f(x) = \sin(2x) - \cos(x)\). Our original inequality is thus equivalent to \(f(x) > 0\). The domain of \(f\) is all real numbers, so we can advance to finding the zeros of \(f\). Setting \(f(x) = 0\) yields \(\sin(2x) - \cos(x) = 0\), which, by way of the Double-Angle Identity for sine, becomes \(2\sin(x)\cos(x) - \cos(x) = 0\) or \(\cos(x) (2\sin(x) - 1) = 0\). From \(\cos(x) = 0\), we get \(x = \frac{\pi}{2} + \pi k\) for integers \(k\) of which only \(x = \frac{\pi}{2}\) and \(x = \frac{3\pi}{2}\) lie in \([0,2\pi)\). For \(2\sin(x) - 1 = 0\), we get \(\sin(x) = \frac{1}{2}\) which gives \(x = \frac{\pi}{6} + 2\pi k\) or \(x = \frac{5\pi}{6} + 2\pi k\) for integers \(k\). Of those, only \(x = \frac{\pi}{6}\) and \(x = \frac{5\pi}{6}\) lie in \([0,2\pi)\). Next, we choose our test values. For \(x =0\) we find \(f(0) = -1\); when \(x = \frac{\pi}{4}\) we get \(f\left(\frac{\pi}{4}\right) =1 - \frac{\sqrt{2}}{2} = \frac{2 - \sqrt{2}}{2}\); for \(x = \frac{3\pi}{4}\) we get \(f\left(\frac{3\pi}{4}\right) =-1 + \frac{\sqrt{2}}{2} = \frac{\sqrt{2} - 2}{2}\); when \(x=\pi\) we have \(f(\pi) = 1\), and lastly, for \(x = \frac{7\pi}{4}\) we get \(f\left(\frac{7\pi}{4}\right) = -1 - \frac{\sqrt{2}}{2} = \frac{-2 - \sqrt{2}}{2}\). We see \(f(x) > 0\) on \(\left(\frac{\pi}{6}, \frac{\pi}{2}\right) \cup \left(\frac{5\pi}{6}, \frac{3\pi}{2}\right)\), so this is our answer. We can use the calculator to check that the graph of \(y = \sin(2x)\) is indeed above the graph of \(y = \cos(x)\) on those intervals.

   

   ---

3. Proceeding as in the last two problems, we rewrite \(\tan(x) \geq 3\) as \(\tan(x) - 3 \geq 0\) and let \(f(x) = \tan(x) - 3\). We note that on \([0,2\pi)\), \(f\) is undefined at \(x =\frac{\pi}{2}\) and \(\frac{3\pi}{2}\), so those values will need the usual disclaimer on the sign diagram.¹⁴ Moving along to zeros, solving \(f(x) = \tan(x) - 3 = 0\) requires the arctangent function. We find \(x = \arctan(3) + \pi k\) for integers \(k\) and of these, only \(x = \arctan(3)\) and \(x = \arctan(3) + \pi\) lie in \([0,2\pi)\). Since \(3 > 0\), we know \(0 < \arctan(3) < \frac{\pi}{2}\) which allows us to position these zeros correctly on the sign diagram. To choose test values, we begin with \(x=0\) and find \(f(0) = -3\). Finding a convenient test value in the interval \(\left(\arctan(3), \frac{\pi}{2}\right)\) is a bit more challenging. Keep in mind that the arctangent function is increasing and is bounded above by \(\frac{\pi}{2}\). This means that the number \(x = \arctan(117)\) is guaranteed¹⁵ to lie between \(\arctan(3)\) and \(\frac{\pi}{2}\). We see that \(f(\arctan(117)) = \tan(\arctan(117)) - 3 = 114\). For our next test value, we take \(x = \pi\) and find \(f(\pi) = -3\). To find our next test value, we note that since \(\arctan(3) < \arctan(117) < \frac{\pi}{2}\), it follows¹⁶ that \(\arctan(3) + \pi < \arctan(117) + \pi < \frac{3\pi}{2}\). Evaluating \(f\) at \(x = \arctan(117) + \pi\) yields \(f(\arctan(117)+\pi) = \tan(\arctan(117) + \pi) -3 = \tan(\arctan(117)) - 3 = 114\). We choose our last test value to be \(x = \frac{7\pi}{4}\) and find \(f\left(\frac{7\pi}{4}\right) = -4\). Since we want \(f(x) \geq 0\), we see that our answer is \(\left[ \arctan(3), \frac{\pi}{2}\right) \cup \left[\arctan(3)+\pi, \frac{3\pi}{2}\right)\). Using the graphs of \(y = \tan(x)\) and \(y = 3\), we see when the graph of the former is above (or meets) the graph of the latter.

   

Subsection Footnotes

¹³ See Example 3.1.5, Example 6.3.2, and Example 6.4.2 for discussion of this technique.

¹⁴ See Section 3.1 for a discussion of the non-standard character known as the interrobang.

¹⁵ We could have chosen any value \(\arctan (t)\) where \(t>3\).

¹⁶ ...by adding \(\pi\) through the inequality...

---

Computing Domains of Nonstandard Trigonometric Functions

We now provide an example that puts solving equations and inequalities to good use – finding domains of functions.

Example \( \PageIndex{6} \)

Express the domain of the following functions using extended interval notation.¹⁷

1. \(f(x) = \csc\left(2x + \frac{\pi}{3}\right)\)
2. \(f(x) = \dfrac{\sin(x)}{2\cos(x) - 1}\)
3. \(f(x) = \sqrt{1 - \cot(x)}\)

Solution

1. To find the domain of \(f(x) = \csc\left(2x + \frac{\pi}{3}\right)\), we rewrite \(f\) in terms of sine as \(f(x) = \frac{1}{\sin\left(2x + \frac{\pi}{3}\right)}\). Since the sine function is defined everywhere, our only concern comes from zeros in the denominator. Solving \(\sin\left(2x + \frac{\pi}{3}\right) = 0\), we get \(x = -\frac{\pi}{6} + \frac{\pi}{2} k\), where \(k \in \mathbb{Z}\). In set-builder notation, our domain is \(\left\{x: x \neq-\frac{\pi}{6}+\frac{\pi}{2} k \text {, where } k \in \mathbb{Z}\right\}\).
   To help visualize the domain, we follow the old mantra "When in doubt, write it out!" We get \(\left\{x: x \neq-\frac{\pi}{6}, \frac{2 \pi}{6},-\frac{4 \pi}{6}, \frac{5 \pi}{6},-\frac{7 \pi}{6}, \frac{8 \pi}{6}, \ldots\right\}\), where we have kept the denominators \(6\) throughout to help see the pattern. Graphing the situation on a numberline, we have

   

   Proceeding as we did in Section 10.3, we let \(x_{k}\) denote the \(k\)th number excluded from the domain and we have \(x_{k} = -\frac{\pi}{6} + \frac{\pi}{2} k = \frac{(3k-1)\pi}{6}\) for \(k \in \mathbb{Z}\). The intervals which comprise the domain are of the form \(\left(x_{k}, x_{k+1} \right) = \left(\frac{(3k-1)\pi}{6}, \frac{(3k+2)\pi}{6} \right)\) as \(k\) runs through the integers. Using extended interval notation, we have that the domain is\[\bigcup_{k = -\infty}^{\infty} \left(\dfrac{(3k-1)\pi}{6}, \dfrac{(3k+2)\pi}{6} \right)\nonumber\]We can check our answer by substituting in values of \(k\) to see that it matches our diagram.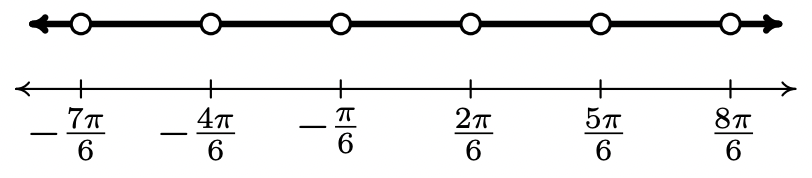

   ---

2. Since the domains of \(\sin(x)\) and \(\cos(x)\) are all real numbers, the only concern when finding the domain of \(f(x) = \frac{\sin(x)}{2\cos(x) - 1}\) is division by zero so we set the denominator equal to zero and solve. From \(2\cos(x) - 1 = 0\) we get \(\cos(x) = \frac{1}{2}\) so that \(x = \frac{\pi}{3} + 2\pi k\) or \(x = \frac{5\pi}{3} + 2\pi k\) for integers \(k\). Using set-builder notation, the domain is \(\left\{x: x \neq \frac{\pi}{3}+2 \pi k \text { and } x \neq \frac{5 \pi}{3}+2 \pi k \text {, where } k \in \mathbb{Z}\right\}\), or \(\left\{ x : x \neq \pm \frac{\pi}{3}, \pm \frac{5\pi}{3}, \pm \frac{7\pi}{3}, \pm \frac{11\pi}{3}, \ldots \right\}\), so we have

   

   Unlike the previous example, we have two different families of points to consider, and we present two ways of dealing with this kind of situation. One way is to generalize what we did in the previous example and use the formulas we found in our domain work to describe the intervals. To that end, we let \(a_{k} = \frac{\pi}{3} + 2\pi k = \frac{(6k+1)\pi}{3}\) and \(b_{k} = \frac{5\pi}{3} + 2\pi k = \frac{(6k+5) \pi}{3}\) for integers \(k\). The goal now is to write the domain in terms of the \(a\)’s an \(b\)’s. We find \(a_0 = \frac{\pi}{3}\), \(a_{1} = \frac{7\pi}{3}\), \(a_{-1} = -\frac{5\pi}{3}\), \(a_{2} = \frac{13\pi}{3}\), \(a_{-2} = -\frac{11\pi}{3}\), \(b_0 = \frac{5\pi}{3}\), \(b_{1} = \frac{11\pi}{3}\), \(b_{-1} = -\frac{\pi}{3}\), \(b_{2} = \frac{17\pi}{3}\) and \(b_{-2} = -\frac{7\pi}{3}\). Hence, in terms of the \(a\)’s and \(b\)’s, our domain is\[\ldots\left(a_{-2}, b_{-2}\right) \cup\left(b_{-2}, a_{-1}\right) \cup\left(a_{-1}, b_{-1}\right) \cup\left(b_{-1}, a_{0}\right) \cup\left(a_{0}, b_{0}\right) \cup\left(b_{0}, a_{1}\right) \cup\left(a_{1}, b_{1}\right) \cup \ldots\nonumber\]If we group these intervals in pairs, \(\left(a_{-2}, b_{-2} \right) \cup \left(b_{-2}, a_{-1} \right)\), \(\left(a_{-1}, b_{-1} \right)\cup \left(b_{-1}, a_0 \right)\), \(\left(a_0, b_0 \right)\cup \left(b_0, a_{1} \right)\) and so forth, we see a pattern emerge of the form \(\left(a_{k}, b_{k} \right)\cup \left(b_{k}, a_{k+1} \right)\) for integers \(k\) so that our domain can be written as\[\bigcup_{k=-\infty}^{\infty}\left(a_{k}, b_{k}\right) \cup\left(b_{k}, a_{k+1}\right)=\bigcup_{k=-\infty}^{\infty}\left(\frac{(6 k+1) \pi}{3}, \frac{(6 k+5) \pi}{3}\right) \cup\left(\frac{(6 k+5) \pi}{3}, \frac{(6 k+7) \pi}{3}\right)\nonumber\]A second approach to the problem exploits the periodic nature of \(f\). Since \(\cos(x)\) and \(\sin(x)\) have period \(2\pi\), it’s not too difficult to show the function \(f\) repeats itself every \(2\pi\) units.¹⁸ This means if we can find a formula for the domain on an interval of length \(2\pi\), we can express the entire domain by translating our answer left and right on the \(x\)-axis by adding integer multiples of \(2\pi\). One such interval that arises from our domain work is \(\left[\frac{\pi}{3}, \frac{7\pi}{3}\right]\). The portion of the domain here is \(\left(\frac{\pi}{3}, \frac{5\pi}{3}\right) \cup \left(\frac{5\pi}{3}, \frac{7\pi}{3}\right)\). Adding integer multiples of \(2\pi\), we get the family of intervals \(\left(\frac{\pi}{3} + 2\pi k, \frac{5\pi}{3} + 2\pi k \right) \cup \left(\frac{5\pi}{3} + 2\pi k, \frac{7\pi}{3} + 2\pi k\right)\) for integers \(k\). We leave it to the reader to show that getting common denominators leads to our previous answer.

   ---

3. To find the domain of \(f(x) = \sqrt{1-\cot(x)}\), we first note that, due to the presence of the \(\cot(x)\) term, \(x \neq \pi k\) for integers \(k\). Next, we recall that for the square root to be defined, we need \(1 - \cot(x) \geq 0\). Unlike the inequalities we solved in Example \( \PageIndex{5} \), we are not restricted here to a given interval. Our strategy is to solve this inequality over \((0,\pi)\) (the same interval which generates a fundamental cycle of cotangent) and then add integer multiples of the period, in this case, \(\pi\). We let \(g(x) = 1 - \cot(x)\) and set about making a sign diagram for \(g\) over the interval \((0,\pi)\) to find where \(g(x) \geq 0\). We note that \(g\) is undefined for \(x = \pi k\) for integers \(k\), in particular, at the endpoints of our interval \(x = 0\) and \(x = \pi\). Next, we look for the zeros of \(g\). Solving \(g(x) = 0\), we get \(\cot(x) = 1\) or \(x = \frac{\pi}{4} + \pi k\) for integers \(k\) and only one of these, \(x = \frac{\pi}{4}\), lies in \((0,\pi)\). Choosing the test values \(x = \frac{\pi}{6}\) and \(x = \frac{\pi}{2}\), we get \(g\left(\frac{\pi}{6}\right) = 1 - \sqrt{3}\), and \(g\left(\frac{\pi}{2}\right) = 1\).

   

   We find \(g(x) \geq 0\) on \(\left[\frac{\pi}{4}, \pi \right)\). Adding multiples of the period we get our solution to consist of the intervals \(\left[\frac{\pi}{4} + \pi k, \pi + \pi k \right) = \left[\frac{(4k+1)\pi}{4}, (k+1)\pi \right)\). Using extended interval notation, we express our final answer as\[\bigcup_{k = -\infty}^{\infty} \left[\dfrac{(4k+1)\pi}{4}, (k+1)\pi \right)\nonumber\]

Subsection Footnotes

¹⁷ See Section 10.3 for details about this notation.

¹⁸ This doesn’t necessarily mean the period of \(f\) is \(2 \pi\). The tangent function is comprised of \(\cos (x)\) and \(\sin (x)\), but its period is half theirs. The reader is invited to investigate the period of \(f\).

---

Solving Equations and Inequalities Involving Inverse Trigonometric Functions

We close this section with an example which demonstrates how to solve equations and inequalities involving the inverse trigonometric functions.

Example \( \PageIndex{7} \)

Solve the following equations and inequalities analytically. Check your answers using a graphing utility.

1. \(\arcsin (2 x)=\frac{\pi}{3}\)
2. \(4 \arccos (x)-3 \pi=0\)
3. \(3 \operatorname{arcsec}(2 x-1)+\pi=2 \pi\)
4. \(4 \arctan ^{2}(x)-3 \pi \arctan (x)-\pi^{2}=0\)
5. \(\pi^{2}-4 \arccos ^{2}(x)<0\)
6. \(4 \operatorname{arccot}(3 x)>\pi\)

Solution

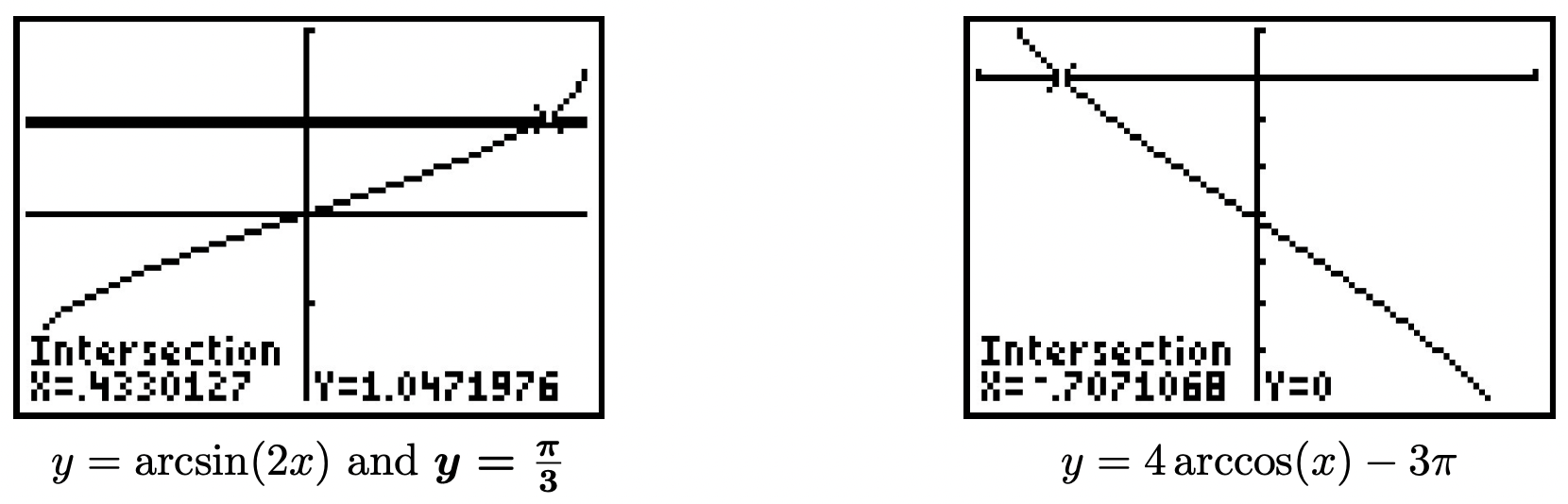
1. To solve \(\arcsin (2 x)=\frac{\pi}{3}\), we first note that \(\frac{\pi}{3}\) is in the range of the arcsine function (so a solution exists!) Next, we exploit the inverse property of sine and arcsine from Theorem 10.6.1 \[\begin{aligned} \arcsin (2 x) &=\frac{\pi}{3} \\ \sin (\arcsin (2 x)) &=\sin \left(\frac{\pi}{3}\right) \\ 2 x &=\frac{\sqrt{3}}{2} \quad \text { Since } \sin (\arcsin (u))=u \\ x &=\frac{\sqrt{3}}{4} \end{aligned}\nonumber\] Graphing \(y=\arcsin (2 x)\) and the horizontal line \(y=\frac{\pi}{3}\), we see they intersect at \(\frac{\sqrt{3}}{4} \approx 0.4430\).

   ---

2. Our first step in solving \(4 \arccos (x)-3 \pi=0\) is to isolate the arccosine. Doing so, we get \(\arccos (x)=\frac{3 \pi}{4}\). Since \(\frac{3 \pi}{4}\) is in the range of arccosine, we may apply Theorem 10.6.1 \[\begin{aligned} \arccos (x) &=\frac{3 \pi}{4} \\ \cos (\arccos (x)) &=\cos \left(\frac{3 \pi}{4}\right) \\ x &=-\frac{\sqrt{2}}{2} \quad \text { Since } \cos (\arccos (u))=u \end{aligned}\nonumber\] The calculator confirms \(y=4 \arccos (x)-3 \pi\) crosses \(y=0\) (the x-axis) at \(-\frac{\sqrt{2}}{2} \approx-0.7071\).

   

   ---

3. From \(3 \operatorname{arcsec}(2 x-1)+\pi=2 \pi\), we get \(\operatorname{arcsec}(2 x-1)=\frac{\pi}{3}\). As we saw in Section 10.6, there are two possible ranges for the arcsecant function. Fortunately, both ranges contain \(\frac{\pi}{3}\). Applying Theorem 10.6.4, we get \[\begin{aligned} \operatorname{arcsec}(2 x-1) &=\frac{\pi}{3} \\ \sec (\operatorname{arcsec}(2 x-1)) &=\sec \left(\frac{\pi}{3}\right) \\ 2 x-1 &=2 \quad \text { Since } \sec (\operatorname{arcsec}(u))=u \\ x &=\frac{3}{2} \end{aligned}\nonumber\]To check using our calculator, we need to graph \(y=3 \operatorname{arcsec}(2 x-1)+\pi\). To do so, we make use of the identity \(\operatorname{arcsec}(u)=\arccos \left(\frac{1}{u}\right)\) from Theorem 10.6.4.¹⁹ We see the graph of \(y=3 \arccos \left(\frac{1}{2 x-1}\right)+\pi\) and the horizontal line \(y=2 \pi\) intersect at \(\frac{3}{2}=1.5\).

   ---

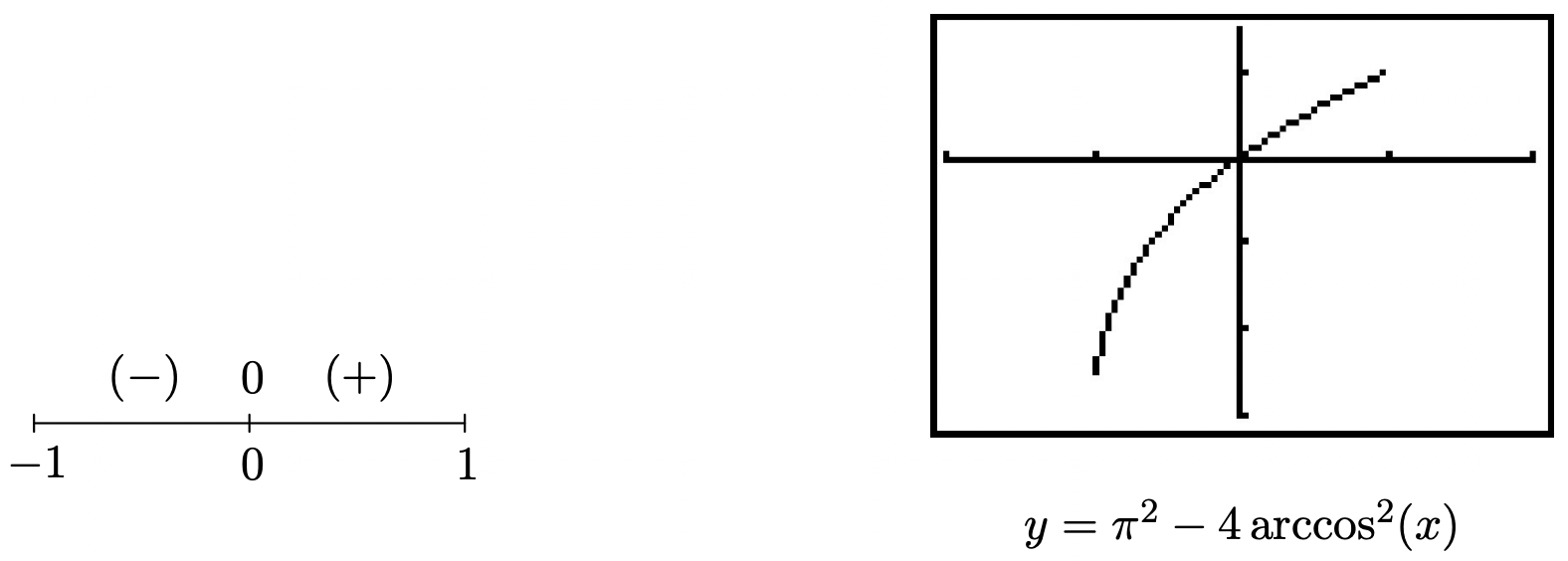
4. With the presence of both \(\arctan ^{2}(x)\left(=(\arctan (x))^{2}\right)\) and \(\arctan (x)\), we substitute \(u=\arctan (x)\). The equation \(4 \arctan ^{2}(x)-3 \pi \arctan (x)-\pi^{2}=0\) becomes \(4 u^{2}-3 \pi u-\pi^{2}=0\). Factoring,²⁰ we get \((4 u+\pi)(u-\pi)=0\), so \(u=\arctan (x)=-\frac{\pi}{4}\) or \(u=\arctan (x)=\pi\). Since \(-\frac{\pi}{4}\) is in the range of arctangent, but \(\pi\) is not, we only get solutions from the first equation. Using Theorem 10.6.2, we get \[\begin{aligned} \arctan (x) &=-\frac{\pi}{4} \\ \tan (\arctan (x)) &=\tan \left(-\frac{\pi}{4}\right) \\
   x &=-1 \quad \text { Since } \tan (\arctan (u))=u \end{aligned}\nonumber\] The calculator verifies our result.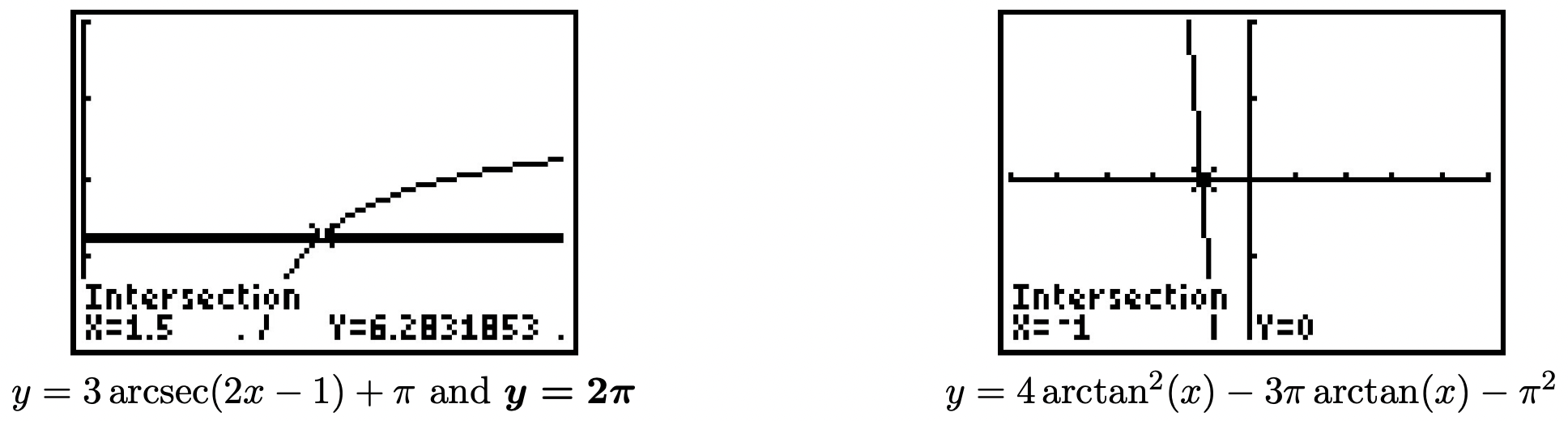

   

   ---

5. Since the inverse trigonometric functions are continuous on their domains, we can solve inequalities featuring these functions using sign diagrams. Since all of the nonzero terms of \(\pi^{2}-4 \arccos ^{2}(x)<0\) are on one side of the inequality, we let \(f(x)=\pi^{2}-4 \arccos ^{2}(x)\) and note the domain of \(f\) is limited by the \(\arccos (x)\) to [−1, 1]. Next, we find the zeros of \(f\) by setting \(f(x)=\pi^{2}-4 \arccos ^{2}(x)=0\). We get \(\arccos (x)=\pm \frac{\pi}{2}\), and since the range of arccosine is \([0, \pi]\), we focus our attention on \(\arccos (x)=\frac{\pi}{2}\). Using Theorem 10.6.1, we get \(x=\cos \left(\frac{\pi}{2}\right)=0\) as our only zero. Hence, we have two test intervals, [−1, 0) and (0, 1]. Choosing test values \(x=\pm 1\), we get \(f(-1)=-3 \pi^{2}<0\) and \(f(1)=\pi^{2}>0\). Since we are looking for where \(f(x)=\pi^{2}-4 \arccos ^{2}(x)<0\), our answer is [−1, 0). The calculator confirms that for these values of \(x\), the graph of \(y=\pi^{2}-4 \arccos ^{2}(x)\) is below \(y=0\) (the x-axis).

   

   ---

6. To begin, we rewrite \(4 \operatorname{arccot}(3 x)>\pi \text { as } 4 \operatorname{arccot}(3 x)-\pi>0\). We let \(f(x)=4 \operatorname{arccot}(3 x)-\pi\), and note the domain of \(f\) is all real numbers, \((-\infty, \infty)\). To find the zeros of \(f\), we set \(f(x)=4 \operatorname{arccot}(3 x)-\pi=0\) and solve. We get \(\operatorname{arccot}(3 x)=\frac{\pi}{4}\), and since \(\frac{\pi}{4}\) is in the range of arccotangent, we may apply Theorem 10.6.2 and solve \[\begin{aligned} \operatorname{arccot}(3 x) &=\frac{\pi}{4} \\ \cot (\operatorname{arccot}(3 x)) &=\cot \left(\frac{\pi}{4}\right) \\ 3 x &=1 \quad \text { Since } \cot (\operatorname{arccot}(u))=u . \\ x &=\frac{1}{3} \end{aligned}\nonumber\]Next, we make a sign diagram for \(f\). Since the domain of \(f\) is all real numbers, and there is only one zero of \(f\), \(x=\frac{1}{3}\), we have two test intervals, \(\left(-\infty, \frac{1}{3}\right)\) and \(\left(\frac{1}{3}, \infty\right)\). Ideally, we wish to find test values \(x\) in these intervals so that \(\operatorname{arccot}(4 x)\) corresponds to one of our oft-used ‘common’ angles. After a bit of computation,²¹ we choose \(x = 0\) for \(x<\frac{1}{3}\) and for \(x>\frac{1}{3}\), we choose \(x=\frac{\sqrt{3}}{3}\). We find \(f(0)=\pi>0\) and \(f\left(\frac{\sqrt{3}}{3}\right)=-\frac{\pi}{3}<0\). Since we are looking for where \(f(x)=4 \operatorname{arccot}(3 x)-\pi>0\), we get our answer \(\left(-\infty, \frac{1}{3}\right)\). To check graphically, we use the technique in number 2c of Example 10.6.5 in Section 10.6 to graph \(y=4 \operatorname{arccot}(3 x)\) and we see it is above the horizontal line \(y=\pi \text { on }\left(-\infty, \frac{1}{3}\right)=(-\infty, 0 . \overline{3})\).

   

Subsection Footnotes

¹⁹ Since we are checking for solutions where arcsecant is positive, we know \(u=2 x-1 \geq 1\), and so the identity applies in both cases.

²⁰ It’s not as bad as it looks... don’t let the \(\pi\) throw you!

²¹ Set \(3x\) equal to the cotangents of the "common angles" and choose accordingly.