10.5: Graphs of the Trigonometric Functions

In this section, we return to our discussion of the circular (trigonometric) functions as functions of real numbers and pick up where we left off in Sections 10.2 and 10.3. As usual, we begin our study with the functions \(f(t) = \cos(t)\) and \(g(t) = \sin(t)\).

---

Base Graphs of the Cosine and Sine Functions

From Theorem 10.2.7 in Section 10.2, we know that the domain of \(f(t) = \cos(t)\) and of \(g(t) = \sin(t)\) is all real numbers, \((-\infty, \infty),\) and the range of both functions is \([-1,1]\). The Even / Odd Identities in Theorem 10.4.1 tell us \(\cos(-t) = \cos(t)\) for all real numbers \(t\) and \(\sin(-t) = -\sin(t)\) for all real numbers \(t\). This means \(f(t) = \cos(t)\) is an even function, while \(g(t) = \sin(t)\) is an odd function.¹ Another important property of these functions is that for coterminal angles \(\alpha\) and \(\beta\), \(\cos(\alpha) = \cos(\beta)\) and \(\sin(\alpha) = \sin(\beta)\). Said differently, \(\cos(t + 2\pi k) = \cos(t)\) and \(\sin(t + 2\pi k) = \sin(t)\) for all real numbers \(t\) and any integer \(k\). This last property is given a special name.

Definition: Periodic Function

A function \(f\) is said to be periodic if there is a real number \(c\) so that \(f(t+c) = f(t)\) for all real numbers \(t\) in the domain of \(f\). The smallest positive number \(p\) for which \(f(t+p) = f(t)\) for all real numbers \(t\) in the domain of \(f\), if it exists, is called the period of \(f\).

We have already seen a family of periodic functions in Section 2.1: the constant functions. However, despite being periodic, a constant function has no period. (We’ll leave that odd gem as an exercise for you.)

Returning to the circular functions, we see that by the definition of a periodic function, \(f(t) = \cos(t)\) is periodic, since \(\cos(t + 2\pi k) = \cos(t)\) for any integer \(k\). To determine the period of \(f\), we need to find the smallest real number \(p\) so that \(f(t+p) = f(t)\) for all real numbers \(t\) or, said differently, the smallest positive real number \(p\) such that \(\cos(t+p) = \cos(t)\) for all real numbers \(t\). We know that \(\cos(t + 2\pi) = \cos(t)\) for all real numbers \(t\) but the question remains if any smaller real number will do the trick. Suppose \(p>0\) and \(\cos(t + p) = \cos(t)\) for all real numbers \(t\). Then, in particular, \(\cos(0+p) = \cos(0)\) so that \(\cos(p) = 1\). From this we know \(p\) is a multiple of \(2\pi\) and, since the smallest positive multiple of \(2\pi\) is \(2\pi\) itself, we have the result. Similarly, we can show \(g(t) = \sin(t)\) is also periodic with \(2\pi\) as its period.² Having period \(2\pi\) essentially means that we can completely understand everything about the functions \(f(t) = \cos(t)\) and \(g(t) = \sin(t)\) by studying one interval of length \(2\pi\), say \([0,2\pi]\).³

One last property of the functions \(f(t) = \cos(t)\) and \(g(t) = \sin(t)\) is worth pointing out: both of these functions are continuous and smooth. Recall from Section 3.1 that geometrically this means the graphs of the cosine and sine functions have no jumps, gaps, holes in the graph, asymptotes, corners or cusps. As we shall see, the graphs of both \(f(t) = \cos(t)\) and \(g(t) = \sin(t)\) meander nicely and don’t cause any trouble. We summarize these facts in the following theorem.

Theorem \(\PageIndex{1}\): Properties of the Cosine and Sine Functions

The function \(f(x) = \cos(x)\) has domain \((-\infty, \infty)\) has range \([-1,1]\) is continuous and smooth is even has period \(2\pi\)

The function \(g(x) = \sin(x)\) has domain \((-\infty, \infty)\) has range \([-1,1]\) is continuous and smooth is odd has period \(2\pi\)

In Theorem \( \PageIndex{1} \), we followed the convention established in Section 1.6 and used \(x\) as the independent variable and \(y\) as the dependent variable.⁴ This allows us to turn our attention to graphing the cosine and sine functions in the Cartesian Plane.

To graph \(y = \cos(x)\), we make a table as we did in Section 1.6 using some of the "common values" of \(x\) in the interval \([0,2\pi]\). This generates a portion of the cosine graph, which we call the "fundamental cycle" of \(y = \cos(x)\).

Figure \( \PageIndex{1} \): The fundamental cycle of \( y = \cos{(x)} \).

A few things about the graph above are worth mentioning. First, Figure \( \PageIndex{1} \) represents only part of the graph of \(y = \cos(x)\). To get the entire graph, we imagine "copying and pasting" this graph end to end infinitely in both directions (left and right) on the \(x\)-axis. Secondly, the vertical scale in Figure \( \PageIndex{1} \) has been greatly exaggerated for clarity and aesthetics. Below is an accurate-to-scale graph of \(y = \cos(x)\) showing several cycles with the "fundamental cycle" plotted thicker than the others. The graph of \(y=\cos(x)\) is usually described as "wavelike" – indeed, many of the applications involving the cosine and sine functions feature modeling wavelike phenomena.

Figure \( \PageIndex{2} \): An accurately scaled graph of \(y=\cos (x)\).

We can plot the fundamental cycle of the graph of \(y = \sin(x)\) similarly, with similar results.

Figure \( \PageIndex{3} \): The fundamental cycle of \( y = \sin{(x)} \).

As with the graph of \(y=\cos(x)\), we provide an accurately scaled graph of \(y = \sin(x)\) below with the fundamental cycle highlighted.

Figure \( \PageIndex{4} \): An accurately scaled graph \(y=\sin (x)\).

It is no accident that the graphs of \(y = \cos(x)\) and \(y = \sin(x)\) are so similar. Using a Cofunction Identity along with the Even Property of cosine, we have

\[\sin(x) = \cos\left(\dfrac{\pi}{2} - x\right) = \cos\left(-\left(x - \dfrac{\pi}{2}\right)\right) = \cos\left(x - \dfrac{\pi}{2}\right).\nonumber\]

Recalling Section 1.7, we see from this formula that the graph of \(y=\sin(x)\) in Figure \( \PageIndex{3} \) is the result of shifting the graph of \(y = \cos(x)\) from Figure \( \PageIndex{1} \) to the right \(\frac{\pi}{2}\) units. A visual inspection confirms this.

Subsection Footnotes

¹ See Section 1.6 for a review of these concepts.

² Alternatively, we can use the Cofunction Identities in Theorem 10.4.3 to show that \(g(t)=\sin (t)\) is periodic with period \(2 \pi\) since \(g(t)=\sin (t)=\cos \left(\frac{\pi}{2}-t\right)=f\left(\frac{\pi}{2}-t\right)\).

³ Technically, we should study the interval \([0,2 \pi)\), since whatever happens at \(t=2 \pi\) is the same as what happens at \(t = 0\). As we will see shortly, \(t=2 \pi\) gives us an extra "check" when we go to graph these functions. In some advanced texts, the interval of choice is \([-\pi, \pi)\).

⁴ The use of \(x\) and \(y\) in this context is not to be confused with the \(x\)- and \(y\)-coordinates of points on the Unit Circle which define cosine and sine. Using the term "trigonometric function" as opposed to "circular function" can help with that, but one could then ask, "Hey, where’s the triangle?"

---

Transformations of the Cosine and Sine Functions

It's natural to want to graph transformations of the cosine and sine functions once you have their "base graphs." These transformations get the special name "sinusoids." Roughly speaking, a sinusoidal function is the result of taking the basic graph of \(f(x) = \cos(x)\) (Figure \( \PageIndex{1} \)) or \(g(x) = \sin(x)\) (Figure \( \PageIndex{2} \)) and performing any of the transformations⁵ mentioned in Section 1.7. 

Before we step too deeply into the graphing theory of sinusoidal functions, let's recall some information from Section 1.7. Suppose we need to graph the function\[ h(x) = A f(Bx + C) + D. \nonumber\]Let's further suppose that \( B \gt 0 \). This is a requirement for our graphing conversation surrounding trigonometric functions. We can always force \( B \gt 0 \) by using the Even/Odd Properties of the trigonometric functions. Finally, to get to the proper form from Section 1.7 we factor the argument⁶ to arrive at \[h(x) = A f\left( B \left(x + \dfrac{C}{B} \right) \right) + D, \label{trans1} \]again, where \( B \gt 0 \). To help us transition to a "trigonometric graphing" mindset, the table below lists our previous knowledge about the effects of the values of \( A \), \( B \), \( C \),⁷ and \( D \) on the graph of the transformation of \( f \) along with language will will be using from this point forward concerning those same concepts or values.

\[ \begin{array}{|c|c|l|c|}
\hline \text{Parameter} & \text{Condition} & \text{General Effect on any Function} & \text{Related Concept(s) in Trigonometry} \\
\hline & |A| \gt 1 & \text{vertical stretch by a factor of }|A| & \text{Amplitude} \\
A & 0 \lt |A| \lt 1 & \text{vertical compression by a factor of }|A| & \text{and} \\
 & A \lt 0 & \text{reflection (vertically) about the }x\text{-axis} & \text{Reflection} \\
\hline & |B| \gt 1 & \text{horizontal compression by a factor of }\frac{1}{|B|} & \text{Period} \\
B & 0 \lt |B| \lt 1 & \text{horizontal stretch by a factor of }\frac{1}{|B|} & \text{and} \\
 & B \lt 0 & \text{reflection (horizontally) about the }y\text{-axis} & \text{Step Size} \\
\hline & \frac{B}{C} \lt 0 & \text{horizontal shift to the right by }\left|\frac{B}{C}\right|\text{ units} & \text{Phase Shift} \\
\frac{B}{C} & & & \text{and} \\
& \frac{B}{C} \gt 0 & \text{horizontal shift to the left by }\frac{B}{C}\text{ units} & \text{Reflection} \\
\hline & D \lt 0 & \text{vertical shift down by }\left|D\right|\text{ units} & \\
D & & & \text{Midline Shift} \\
& D \gt 0 & \text{vertical shift up by }D\text{ units} & \\
\hline \end{array} \nonumber \]

So what are "amplitude," "period", "step size," "phase shift," and "midline shift?"

The amplitude of the sinusoid is a measure of how "tall" the wave is, as indicated in Figure \( \PageIndex{3} \) below. The amplitude of the standard cosine and sine functions is \(1\), but vertical scalings can alter this - this is why amplitude is associated with the value of \( A \). In fact, the amplitude is defined to be \( |A| \). From Figure \( \PageIndex{3} \), you can see the amplitude is the distance between the midline (to be defined shortly) and the local extrema of the sinusoidal function.

Figure \( \PageIndex{3} \): An illustration of the baseline (or "midline") of a sinusoidal function, the amplitude, and the period.

We have already discussed the fact that the period is how long it takes for the sinusoid to complete one cycle. The standard period of both \(f(x) = \cos(x)\) and \(g(x) = \sin(x)\) is \(2\pi\). That is, both \( f(x) = \cos{(x)} \) and \( g(x) = \sin{(x)} \) go through one full cycle, or one fundamental cycle, on the interval \( 0 \leq x \leq 2\pi \). What happens if there is a horizontal scaling? Consider \( f_1(x) = \cos{(Bx)} \) and \( g_1(x) = \sin{(Bx)} \) (remember, it's assumed we used the Even / Odd Properties to force \( B \) to be positive). The arguments of these functions must meander from \( 0 \) to \( 2\pi \) in order for these functions to go through one fundamental cycle. That is, these functions go through one fundamental cycle on the interval \( 0 \leq Bx \leq 2 \pi \). Solving for \( x \), we get \( 0 \leq x \leq \frac{2\pi}{B} \). Hence, the period of a sinusoidal function with horizontal scaling \( B \gt 0 \) is \( \frac{2 \pi}{B} \).

We now arrive at the step size. A very nice feature of sinusoidal functions (as seen in Figures \( \PageIndex{1} \) and \( \PageIndex{2} \)) is the fact that they have five key points that help us graph. For "untransformed" sinusoidal functions, these occur at the values at \(x = 0\), \(\frac{\pi}{2}\), \(\pi\), \(\frac{3\pi}{2}\) and \(2\pi\). These "quarter marks" correspond to quadrantal angles, and as such, mark the location of the zeros and the local extrema of these functions over exactly one period. Since we know the standard period of the cosine and sine functions is \( 2 \pi \), the "quarter marks" partition the interval \( [0, 2\pi] \) into five equally-spaced subintervals.⁸ The length of each subinterval is called the step size and its value is\[ \text{Step Size} = \dfrac{\text{Period}}{4}. \nonumber \]If there is no horizontal scaling, then this value is just\[ \text{Step Size} = \dfrac{\text{Period}}{4} = \dfrac{2 \pi}{4} = \dfrac{\pi}{2}. \nonumber \]Having such characteristics as period and a standard step size to get to the key points makes graphing the cosine and sine functions a little easier than what we encountered in Section 1.7.

The phase shift of the sinusoid is a fancy name for the horizontal shift experienced by the fundamental cycle. We have seen that a phase (horizontal) shift of \(\frac{\pi}{2}\) to the right takes \(f(x) = \cos(x)\) to \(g(x) = \sin(x)\) since \(\cos\left(x - \frac{\pi}{2}\right) = \sin(x)\). As the reader can verify, a phase shift of \(\frac{\pi}{2}\) to the left takes \(g(x) = \sin(x)\) to \(f(x)= \cos(x)\). The phase shift tells us where to start graphing our fundamental cycle.

Finally, the midline shift of a sinusoid is exactly the same as the vertical shift in Section 1.7. Recall from the function \( g(x) = \sec{(x)} \) in Section 1.7, we graphed a "midline" for \( g \) and shifted this midline up and down whenever we had a vertical shift. This will also be the case for graphs of sinusoidal functions (see Figure \( \PageIndex{3} \) above, where the midline is sadly labeled "baseline").

To summarize:

Theorem \(\PageIndex{2}\)

Given a sinusoidal function of the form\[ C(x) = A \cos{(Bx + C)} + D = A \cos{\left( B \left(x + \dfrac{C}{B} \right) \right)} + D \nonumber \]or\[ S(x) = A \sin{(Bx + C)} + D = A \sin{\left( B \left(x + \dfrac{C}{B} \right) \right)} + D, \nonumber \]where \( B \gt 0 \), the Amplitude, Period, Step Size, Phase Shift, and Midline Shift are found via the following formulas:\[ \begin{array}{rcl}
\text{Amplitude} & = & |A| \\
\text{Period} & = & \dfrac{\text{Standard Period}}{B} \\
\text{Step Size} & = & \dfrac{\text{Period}}{4} \\
\text{Phase Shift} & = & -\dfrac{C}{B} \\
\text{Midline Shift} & = & D \\
\end{array} \nonumber \]

We have gone this entire time without dipping into an example. It's time that we solidify all this language with some graphing.

Example \( \PageIndex{1} \)

Graph one cycle of the following functions. State the period of each.

1. \(f(x) = 3 \cos\left(\frac{\pi x - \pi}{2}\right) + 1\)
2. \(g(x) = \frac{1}{2} \sin(\pi - 2x) + \frac{3}{2}\)

Solution

1. Just as we did in Equation \( \ref{trans1} \), we start by rewriting the given function in the form\[ f(x) = A \cos{\left(B \left(x + \dfrac{B}{C} \right) \right)} + D,  \nonumber \]where \( B \gt 0 \). In this case, we have\[ f(x) = 3 \cos{\left( \dfrac{\pi}{2} \left( x - 1 \right)\right)} + 1. \nonumber \]Reading from left-to-right, and using our new language,\[ \begin{array}{rcccl}
   \text{Amplitude} & = & |A| & = & |3| = 3 \\
   \text{Period} & = & \dfrac{\text{Standard Period}}{B} & = & \dfrac{2 \pi}{\pi/2} = 4 \\
   \text{Step Size} & = & \dfrac{\text{Period}}{4} & = & \dfrac{4}{4} = 1 \\
   \text{Phase Shift} & = & -\dfrac{C}{B} & = & -(-1) = 1 \\
   \text{Midline Shift} & = & D & = & 1 \\
   \end{array} \nonumber \]To graph a fundamental cycle of this cosine function, we start by recognizing the coefficient, \( 3 \), is positive, so there is not a vertical reflection. We then go through our list in reverse order. We first graph the Midline.

   

   We then cleanly sketch a "rightside up" cosine function, using our Midline as a "phantom axis."

   

   At this point, we need to plot the five key points. This is as simple as marking the endpoints of the fundamental cycle, the center point, and the center points of the two remaining subintervals.

   

   The first of these points occurs at the Phase Shift (\( x = 1 \)). We get to the second point by adding the Step Size, the third by adding the Step Size again, and so on.

   

   Now that we know the \( x \)-values for those key points, we can accurately place the \( y \)-axis.

   

   Using the Amplitude, we can say the maximum occurs at \( y = 1 + 3 = 4 \) and the minimum occurs at \( y = 1 - 3 = -2 \). Labeling these values on the \( y \)-axis allows us to properly place the \( x \)-axis.

   

2. Proceeding as above, we start by placing \( g \) in the proper form.\[ g(x) = \dfrac{1}{2} \sin{(-2(x - \pi))} + \dfrac{3}{2} = -\dfrac{1}{2} \sin{(2(x - \pi))} +\dfrac{3}{2}. \nonumber \]Note that we used the Even / Odd Properties to force \( B \gt 0 \). From this form, we get the following information:\[ \begin{array}{rcccl}
   \text{Amplitude} & = & |A| & = & \left| -\frac{1}{2} \right| = \frac{1}{2} \\
   \text{Period} & = & \dfrac{\text{Standard Period}}{B} & = & \dfrac{2 \pi}{2} = \pi \\
   \text{Step Size} & = & \dfrac{\text{Period}}{4} & = & \dfrac{\pi}{4} \\
   \text{Phase Shift} & = & -\dfrac{C}{B} & = & -(-\pi) = \pi \\
   \text{Midline Shift} & = & D & = & \frac{3}{2} \\
   \end{array} \nonumber \]To graph a fundamental cycle of this sine function, we start by recognizing the coefficient, \( -\frac{1}{2} \), is negative. This means that once we have to graph the sine curve, we will be reflecting it about our Midline. We then go through our list in reverse order. We first graph the Midline.

   

   We then cleanly sketch an "upside down" sine function, using our Midline as a "phantom axis."

   

   At this point, we need to plot the five key points.

   

   To label the key points, we start (on the left) by labeling the first as the Phase Shift and move by the Step Size to get to each subsequent key point.

   

   Let's pause for a moment to notice that, when plotting the key points, we wrote the Phase Shift and the Step Size in the same denominator and we didn't bother simplifying the fractions. I find that students grasp the idea of graphing trigonometric functions and plotting key points much better when such trivial things as reducing fractions via their prerequisite fractional arithmetic is allowed to be ignored. We now accurately place the \( y \)-axis. To do so, we will need to zoom out a little bit.

   

   Finally, using the Amplitude, we can say the maximum occurs at \( y = \frac{3}{2} + \frac{1}{2} = 2 \) and the minimum occurs at \( y = \frac{3}{2} - \frac{1}{2} = 1 \). Labeling these values on the \( y \)-axis allows us to properly place the \( x \)-axis.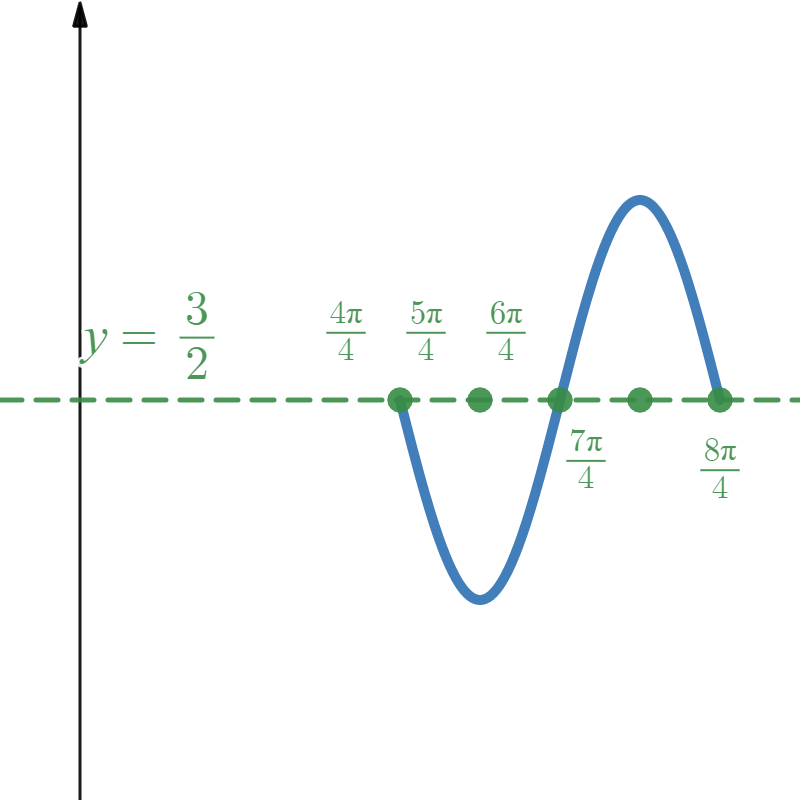

   

In scientific circles, the parameter \(B\), which is stipulated to be positive, is called the (angular) frequency of the sinusoid and is the number of cycles the sinusoid completes over a \(2\pi\) interval. As stated several times already, we can always ensure \(B \gt 0\) using the Even/Odd Identities. For instance, in Example \( \PageIndex{1} \) part b, the angular frequency is \( B = 2 \). That is, the sinusoidal function goes through \( 2 \) full fundamental cycles on any interval of length \( 2 \pi \).

Example \( \PageIndex{2} \)

Below is the graph of one complete cycle of a sinusoid \(y=f(x)\).

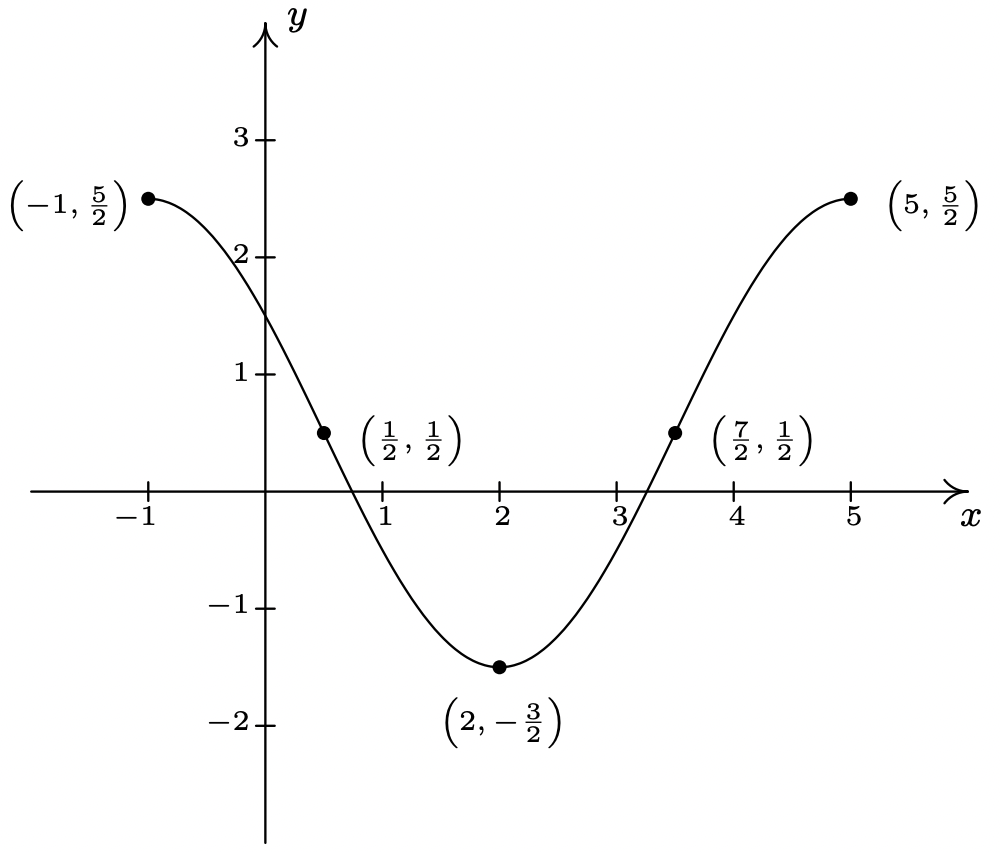
One cycle of \(y=f(x)\).

1. Find a cosine function whose graph matches the graph of \(y = f(x)\).
2. Find a sine function whose graph matches the graph of \(y = f(x)\).

Solution

1. We fit the data to a function of the form \(C(x) = A \cos(B x + C) + D\). Since one cycle is graphed over the interval \([-1,5]\), its period is \(5-(-1) = 6\). Therefore, according to Theorem \( \PageIndex{2} \), \(\text{Period} = 6 = \frac{2\pi}{B}\), so that \(B = \frac{\pi}{3}\). Next, we see that the phase shift is \(-1\), so we have \(\text{Phase Shift} = -\frac{C}{B} = -1\), or \(C = B = \frac{\pi}{3}\). To find the amplitude, note that the range of the sinusoid is \(\left[ -\frac{3}{2}, \frac{5}{2}\right]\). As a result, the amplitude \(A = \frac{1}{2}\left[ \frac{5}{2} - \left(-\frac{3}{2}\right)\right] = \frac{1}{2} (4) = 2.\) Finally, to determine the vertical shift, we average the endpoints of the range to find \(D = \frac{1}{2}\left[ \frac{5}{2} + \left(-\frac{3}{2}\right)\right] = \frac{1}{2}(1) = \frac{1}{2}\). Our final answer is \(C(x) = 2 \cos\left(\frac{\pi}{3} x + \frac{\pi}{3} \right) + \frac{1}{2}\).
2. Most of the work to fit the data to a function of the form \(S(x) = A \sin(B x + C) + D\) is done. The period, amplitude and vertical shift are the same as before with \(B = \frac{\pi}{3}\), \(A = 2\) and \(D = \frac{1}{2}\). The trickier part is finding the phase shift. To that end, we imagine extending the graph of the given sinusoid as in the figure below so that we can identify a cycle beginning at \(\left(\frac{7}{2}, \frac{1}{2}\right)\). Taking the phase shift to be \(\frac{7}{2}\), we get \(-\frac{C}{B} = \frac{7}{2}\), or \(C = -\frac{7}{2} B = -\frac{7}{2}\left(\frac{\pi}{3}\right) = -\frac{7\pi}{6}\). Hence, our answer is \(S(x) = 2 \sin\left(\frac{\pi}{3} x - \frac{7\pi}{6}\right) + \frac{1}{2}\).

Extending the graph of \(y=f(x)\).

Note that each of the answers given in Example \( \PageIndex{2} \) is one choice out of many possible answers. For example, when fitting a sine function to the data, we could have chosen to start at \(\left(\frac{1}{2}, \frac{1}{2}\right)\) taking \(A = -2\). In this case, the phase shift is \(\frac{1}{2}\) so \(C = -\frac{\pi}{6}\) for an answer of \(S(x) = -2 \sin\left(\frac{\pi}{3} x - \frac{\pi}{6}\right) + \frac{1}{2}\). Alternatively, we could have extended the graph of \(y=f(x)\) to the left and considered a sine function starting at \(\left(-\frac{5}{2}, \frac{1}{2}\right)\), and so on. Each of these formulas determine the same sinusoid curve and their formulas are all equivalent using identities.

---

Finding a Sinusoidal Function from the Sum of Sines and Cosines

Connecting Concepts - Differential Equations

In differential equations (as well as in signal analysis and physics), it will become important to rewrite functions of the form\[ f(x) = A \cos(Bx) + B \sin(Bx) \nonumber \]as a single sine (or cosine) function. I discuss how to do this below.

If we use the sum identity for cosine, we can expand the formula to yield \[C(x) = A \cos(B x + C) + D = A\cos(B x) \cos(C) - A \sin(B x)\sin(C) + D.\nonumber\] Similarly, using the sum identity for sine, we get \[S(x) = A \sin(B x + C) + B = A\sin(B x) \cos(C) + A \cos(B x)\sin(C) + D.\nonumber\] Making these observations allows us to recognize (and graph) functions as sinusoids which, at first glance, don’t appear to fit the forms of either \(C(x)\) or \(S(x)\).

Example \( \PageIndex{3} \)

Consider the function \(f(x) = \cos(2x) - \sqrt{3} \sin(2x)\). Find a formula for \(f(x)\):

1. in the form \(C(x) = A \cos(B x + C) + D\) for \(B > 0\)
2. in the form \(S(x) = A \sin(B x + C) + D\) for \(B > 0\)

Check your answers analytically using identities and graphically using a calculator.

Solution

1. The key to this problem is to use the expanded forms of the sinusoid formulas and match up corresponding coefficients. Equating \(f(x) = \cos(2x) - \sqrt{3} \sin(2x)\) with the expanded form of \(C(x) = A \cos(B x + C) + D\), we get\[\cos(2x) - \sqrt{3} \sin(2x) = A\cos(B x) \cos(C) - A \sin(B x)\sin(C) + D\nonumber\]It should be clear that we can take \(B = 2\) and \(D = 0\) to get\[\cos(2x) - \sqrt{3} \sin(2x) = A\cos(2x) \cos(C) - A \sin(2x)\sin(C)\nonumber\]To determine \(A\) and \(C\), a bit more work is involved. We get started by equating the coefficients of the trigonometric functions on either side of the equation. On the left hand side, the coefficient of \(\cos(2x)\) is \(1\), while on the right hand side, it is \(A \cos(C)\). Since this equation is to hold for all real numbers, we must have that \(A \cos(C) = 1\). Similarly, we find by equating the coefficients of \(\sin(2x)\) that \(A \sin(C) = \sqrt{3}\). What we have here is a system of nonlinear equations! We can temporarily eliminate the dependence on \(C\) by using the Pythagorean Identity. We know \(\cos^{2}(C) + \sin^{2}(C) = 1\), so multiplying this by \(A^2\) gives \(A^2\cos^{2}(C) + A^2\sin^{2}(C) = A^2\). Since \(A \cos(C) = 1\) and \(A \sin(C) = \sqrt{3}\), we get \(A^2 = 1^2 + (\sqrt{3})^2 = 4\) or \(A = \pm 2\). Choosing \(A = 2\), we have \(2\cos(C) = 1\) and \(2 \sin(C) = \sqrt{3}\) or, after some rearrangement, \(\cos(C) = \frac{1}{2}\) and \(\sin(C) = \frac{\sqrt{3}}{2}\). One such angle \(C\) which satisfies this criteria is \(C = \frac{\pi}{3}\). Hence, one way to write \(f(x)\) as a sinusoid is \(f(x) = 2 \cos\left(2x + \frac{\pi}{3}\right)\). We can easily check our answer using the sum formula for cosine \[\begin{array}{rcl}
   f(x) & = & 2 \cos\left(2x + \dfrac{\pi}{3}\right) \\
   & = & 2 \left[ \cos(2x) \cos\left(\dfrac{\pi}{3}\right) - \sin(2x) \sin\left(\dfrac{\pi}{3}\right) \right] \\
   & = & 2 \left[ \cos(2x) \left(\dfrac{1}{2}\right) - \sin(2x) \left(\dfrac{\sqrt{3}}{2}\right)\right] \\
   & = & \cos(2x) - \sqrt{3} \sin(2x) \\
   \end{array}\nonumber\]
2. Proceeding as before, we equate \(f(x) = \cos(2x) - \sqrt{3} \sin(2x)\) with the expanded form of \(S(x) = A \sin(B x + C) + D\) to get\[\cos(2x) - \sqrt{3} \sin(2x) = A\sin(B x) \cos(C) + A \cos(B x)\sin(C) + D\nonumber\]Once again, we may take \(B = 2\) and \(D = 0\) so that\[\cos(2x) - \sqrt{3} \sin(2x) = A\sin(2x) \cos(C) + A \cos(2x)\sin(C)\nonumber\]We equate the coefficients of \(\cos(2x)\) on either side and get \(A\sin(C) = 1\) and \(A\cos(C) = -\sqrt{3}\). Using \(A^2\cos^{2}(C) + A^2\sin^{2}(C) = A^2\) as before, we get \(A = \pm 2\), and again we choose \(A = 2\). This means \(2 \sin(C) = 1\), or \(\sin(C) = \frac{1}{2}\), and \(2\cos(C) = -\sqrt{3}\), which means \(\cos(C) = -\frac{\sqrt{3}}{2}\). One such angle which meets these criteria is \(C = \frac{5\pi}{6}\). Hence, we have \(f(x) = 2 \sin\left(2x + \frac{5\pi}{6}\right)\). Checking our work analytically, we have \[\begin{array}{rcl}
   f(x) & = & 2 \sin\left(2x + \dfrac{5\pi}{6}\right) \\
   & = & 2 \left[ \sin(2x) \cos\left(\dfrac{5\pi}{6}\right) + \cos(2x) \sin\left(\dfrac{5\pi}{6}\right) \right] \\
   & = & 2 \left[ \sin(2x) \left(-\dfrac{\sqrt{3}}{2}\right) + \cos(2x) \left(\dfrac{1}{2}\right)\right] \\
   & = & \cos(2x) - \sqrt{3} \sin(2x) \\
   \end{array}\nonumber\]Graphing the three formulas for \(f(x)\) result in the identical curve, verifying our analytic work.

   

It is important to note that in order for the technique presented in Example \( \PageIndex{3} \) to fit a function into one of the forms in Theorem \( \PageIndex{2} \), the arguments of the cosine and sine function must match. That is, while \(f(x) = \cos(2x) - \sqrt{3} \sin(2x)\) is a sinusoid, \(g(x) = \cos(2x) - \sqrt{3} \sin(3x)\) is not.⁹ It is also worth mentioning that, had we chosen \(A = -2\) instead of \(A = 2\) as we worked through Example \( \PageIndex{3} \), our final answers would have looked different. The reader is encouraged to rework Example \( \PageIndex{3} \) using \(A = -2\) to see what these differences are, and then for a challenging exercise, use identities to show that the formulas are all equivalent. The general equations to fit a function of the form \(f(x) = a \, \cos(B x) + b \, \sin(B x) + D\) into one of the forms in Theorem \( \PageIndex{2} \) are explored in the Exercises.

Subsection Footnotes

⁵ We have already seen how the Even/Odd and Cofunction Identities can be used to rewrite \(g(x)=\sin (x)\) as a transformed version of \(f(x)=\cos (x)\), so of course, the reverse is true: \(f(x)=\cos (x)\) can be written as a transformed version of \(g(x)=\sin (x)\). The authors have seen some instances where sinusoids are always converted to cosine functions while in other disciplines, the sinusoids are always written in terms of sine functions. We will discuss the applications of sinusoids in greater detail in Chapter 11. Until then, we will keep our options open.

⁶ Loosely stated, the argument of a trigonometric function is the expression "inside" the function.

⁷ In some scientific and engineering circles, the quantity \(C\) mentioned in Equation \( \ref{trans1} \) is called the phase of the sinusoid; however, we will not be using that language here.

⁸ The idea of "partitioning" an interval into subintervals is a critical concept in Calculus.

⁹ This graph does, however, exhibit sinusoid-like characteristics! Check it out!

---

Base Graphs of the Secant and Cosecant Functions

We now turn our attention to graphing \(y = \sec(x)\). Since \(\sec(x) = \frac{1}{\cos(x)}\), we can use our table of values for the graph of \(y = \cos(x)\) and take reciprocals. We know from Section 10.3 that the domain of \(F(x) = \sec(x)\) excludes all odd multiples of \(\frac{\pi}{2}\), and sure enough, we run into trouble at \(x = \frac{\pi}{2}\) and \(x = \frac{3\pi}{2}\) since \(\cos(x) = 0\) at these values. Using the notation introduced in Section 4.2, we have that as \(x \to \frac{\pi}{2}^{-}\), \(\cos(x) \to 0^{+}\), so \(\sec(x) \to \infty\). (See Section 10.3 for a more detailed analysis.) Similarly, we find that as \(x \to \frac{\pi}{2}^{+}\), \(\sec(x) \to -\infty\); as \(x \to \frac{3\pi}{2}^{-}\), \(\sec(x) \to -\infty\); and as \(x \to \frac{3\pi}{2}^{+}\), \(\sec(x) \to \infty\). This means we have a pair of vertical asymptotes to the graph of \(y = \sec(x)\), \(x = \frac{\pi}{2}\) and \(x = \frac{3\pi}{2}\). Since \(\cos(x)\) is periodic with period \(2\pi\), it follows that \(\sec(x)\) is as well.¹⁰ Below we graph a fundamental cycle of \(y = \sec(x)\) along with a more complete graph obtained by the usual "copying and pasting."¹¹

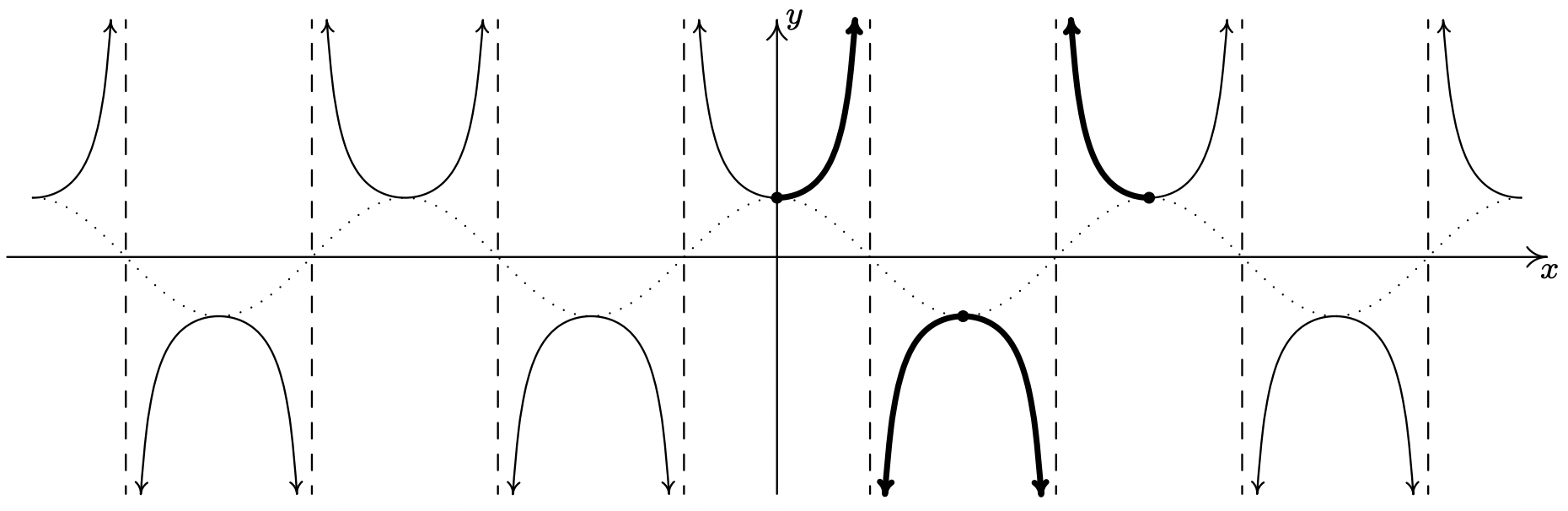
The graph of \(y=\sec (x)\).

As one would expect, to graph \(y = \csc(x)\) we begin with \(y = \sin(x)\) and take reciprocals of the corresponding \(y\)-values. Here, we encounter issues at \(x = 0\), \(x = \pi\) and \(x = 2\pi\). Proceeding with the usual analysis, we graph the fundamental cycle of \(y = \csc(x)\) below along with the dotted graph of \(y=\sin(x)\) for reference. Since \(y = \sin(x)\) and \(y = \cos(x)\) are merely phase shifts of each other, so too are \(y = \csc(x)\) and \(y = \sec(x)\).

The 'fundamental cycle' of \(y=\csc (x)\).

Once again, our domain and range work in Section 10.3 is verified geometrically in the graph of \(y = G(x) = \csc(x)\).

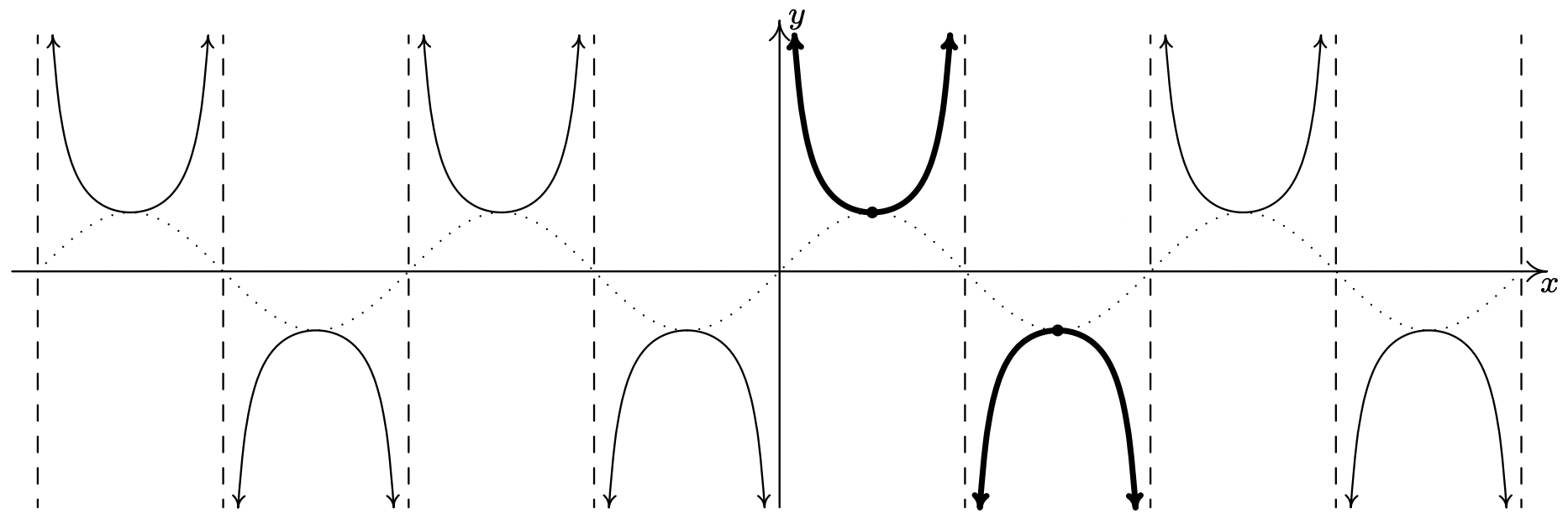
The graph of \(y=\csc (x)\).

Note that, on the intervals between the vertical asymptotes, both \(F(x) = \sec(x)\) and \(G(x) = \csc(x)\) are continuous and smooth. In other words, they are continuous and smooth on their domains.¹² The following theorem summarizes the properties of the secant and cosecant functions. Note that all of these properties are direct results of them being reciprocals of the cosine and sine functions, respectively.

Theorem \(\PageIndex{3}\): Properties of the Secant and Cosecant Functions

• The function \(F(x) = \sec(x)\)
  • has domain \(\left\{x: x \neq \frac{\pi}{2}+\pi k, k \text { is an integer }\right\}=\bigcup_{k=-\infty}^{\infty}\left(\frac{(2 k+1) \pi}{2}, \frac{(2 k+3) \pi}{2}\right)\)
  • has range \(\{ y : |y| \geq 1 \} = (-\infty, -1] \cup [1, \infty)\)
  • is continuous and smooth on its domain
  • is even
  • has period \(2\pi\)
• The function \(G(x) = \csc(x)\)
  • has domain \(\{x: x \neq \pi k, k \text { is an integer }\}=\bigcup_{k=-\infty}^{\infty}(k \pi,(k+1) \pi)\)
  • has range \(\{ y : |y| \geq 1 \} = (-\infty, -1] \cup [1, \infty)\)
  • is continuous and smooth on its domain
  • is odd
  • has period \(2\pi\)

Subsection Footnotes

¹⁰ Provided \(\sec (\alpha)\) and \(\sec (\beta)\) are defined, \(\sec (\alpha)=\sec (\beta)\) if and only if \(\cos (\alpha)=\cos (\beta)\). Hence, \(\sec (x)\) inherits its period from \(\cos (x)\).

¹¹ In Section 10.3, we argued the range of \(F(x)=\sec (x)\) is \((-\infty,-1] \cup[1, \infty)\). We can now see this graphically.

¹² Just like the rational functions in Chapter 4 are continuous and smooth on their domains because polynomials are continuous and smooth everywhere, the secant and cosecant functions are continuous and smooth on their domains since the cosine and sine functions are continuous and smooth everywhere.

---

Transformations of the Secant and Cosecant Functions

In the next example, we discuss graphing more general secant and cosecant curves.

Example \( \PageIndex{4} \)

Graph one cycle of the following functions. State the period of each.

1. \(f(x) = 1 - 2 \sec(2x)\)
2. \(g(x) = \dfrac{\csc(\pi - \pi x) - 5}{3}\)

Solution

1. To graph \(y = 1 - 2 \sec(2x)\), we place it in the form \( h(x) = A f\left( B \left( x + \frac{C}{B} \right) \right) + D \), as we have done with every other example in this section. We get\[ y = -2 \sec{(2 x)} + 1. \nonumber \]We follow the same procedure as in Example \( \PageIndex{1} \) with two modifications. First, we focus on graphing the reciprocal function of the secant, which is the cosine. Once we have graphed \( y = -2 \cos{(2 x)} + 1 \), we note that wherever the cosine curve crosses the midline, the cosine will be zero. As such, the secant will have a vertical asymptote at this same \( x \)-value. Reading \( y = -2 \cos{(2 x)} + 1 \) from left-to-right, we find the following:\[ \begin{array}{rcccl}
   \text{Amplitude} & = & |A| & = & |-2| = 2 \\
   \text{Period} & = & \dfrac{\text{Standard Period}}{B} & = & \dfrac{2 \pi}{2} = \pi \\
   \text{Step Size} & = & \dfrac{\text{Period}}{4} & = & \dfrac{\pi}{4} \\
   \text{Phase Shift} & = & -\dfrac{C}{B} & = & 0 \\
   \text{Midline Shift} & = & D & = & 1 \\
   \end{array} \nonumber \]Graphing the Midline and then cleanly sketching an "upside down" (because \( A = -2 \lt 0 \)) cosine curve, we get

     

   
   Plotting five key points (equally-spaced on the fundamental cycle), labeling the first as the Phase Shift, computing the remaining key points via the Step Size, and finally placing the axes appropriately, we get

     

   Notice that, unlike our previous examples, we decided to "extend" our sketch beyond a single fundamental cycle. This is so you, the reader, can see the secant curve form. Wherever the cosine function crosses the Midline, the value of the cosine will be zero. Therefore, our vertical asymptotes for the secant curve occur exactly at these values of \( x \).

   

   As the cosine function (the blue curve) approaches the line \( y = 1 \) from above, the secant function will tend to infinity. As the cosine function approaches \( y = 1 \) from below, the secant tends to negative infinity. Hence, we get our final curve (shown in black).

   

2. Rather than being descriptive here, we are just going to go through the process as you would on an exam.\[ \begin{array}{rclr}
   g(x) & = & \dfrac{\csc(\pi - \pi x) - 5}{3} & \\
   & = & \dfrac{1}{3} \csc{\left( -\pi \left(x - 1 \right) \right)} - \dfrac{5}{3} & \\
   & = & - \dfrac{1}{3} \csc{\left( \pi \left(x - 1 \right) \right)} - \dfrac{5}{3} & \left( \text{Even/Odd Properties} \right) \\
   \end{array} \nonumber \]Therefore,\[ \begin{array}{rcccl}
   \text{Amplitude} & = & |A| & = & \left| -\dfrac{1}{3} \right| = \dfrac{1}{3} \\
   \text{Period} & = & \dfrac{\text{Standard Period}}{B} & = & \dfrac{2 \pi}{\pi} = 2 \\
   \text{Step Size} & = & \dfrac{\text{Period}}{4} & = & \dfrac{2}{4} = \dfrac{1}{2} \\
   \text{Phase Shift} & = & -\dfrac{C}{B} & = & 1 \\
   \text{Midline Shift} & = & D & = & -\dfrac{5}{3} \\
   \end{array} \nonumber \]
   Graphing the Midline and the "upside down" sine curve, and plotting the five key points, we get

   

   Labeling the first as the Phase Shift and using the Step Size to label the rest, we get

   

   We now use the scale of our Midline to place the \( y \)-axis, label it, and use that to place the \( x \)-axis.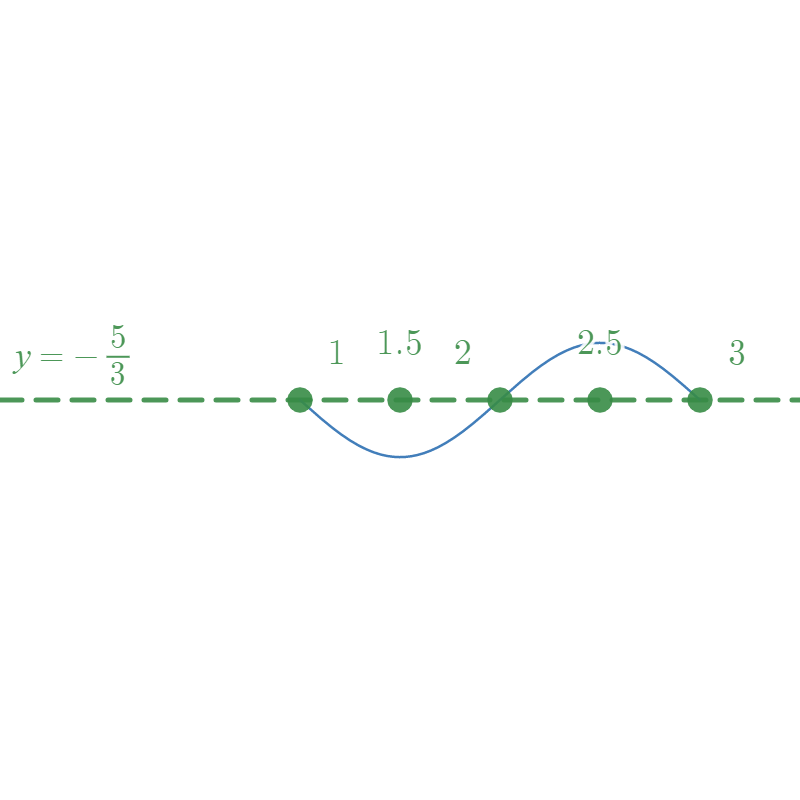

   

   Placing vertical asymptotes wherever the sine curve crosses the Midline, and then graphing the reciprocal of the sine curve, we get

   

Before moving on, it is important to clarify - the only trigonometric functions that have an amplitude are the cosine and the sine. That is, the secant and cosecant do not have amplitudes! However, we use the graphs of the cosine and sine to help us graph the secant and cosecant, respectively. As such, we still mention amplitude when graph the cosine and sine functions.

Another critical observation is that we always graph the vertical asymptotes when graphing the secant and the cosecant. Not doing so is an abomination. Finally, notice that we graphed more than a fundamental cycle in part a of Example \( \PageIndex{4} \), but only graphed a single fundamental cycle in part b. In general, you will only need to graph a single fundamental cycle. The only reason we graphed more than that in part a was to illustrate the periodic behavior of the secant function for the reader.

---

Base Graphs of the Tangent and Cotangent Functions

Finally, we turn our attention to the graphs of the tangent and cotangent functions. When constructing a table of values for the tangent function, we see that \(J(x) = \tan(x)\) is undefined at \(x = \frac{\pi}{2}\) and \(x = \frac{3\pi}{2}\), in accordance with our findings in Section 10.3. As \(x \to \frac{\pi}{2}^{-}\), \(\sin(x) \to 1^{-}\) and \(\cos(x) \to 0^{+}\), so that \(\tan(x) = \frac{\sin(x)}{\cos(x)}\to \infty\) producing a vertical asymptote at \(x = \frac{\pi}{2}\). Using a similar analysis, we get that as \(x \to \frac{\pi}{2}^{+}\), \(\tan(x) \to -\infty\); as \(x \to \frac{3\pi}{2}^{-}\), \(\tan(x) \to \infty\); and as \(x \to \frac{3\pi}{2}^{+}\), \(\tan(x) \to -\infty\). Plotting this information and performing the usual "copy and paste" produces:

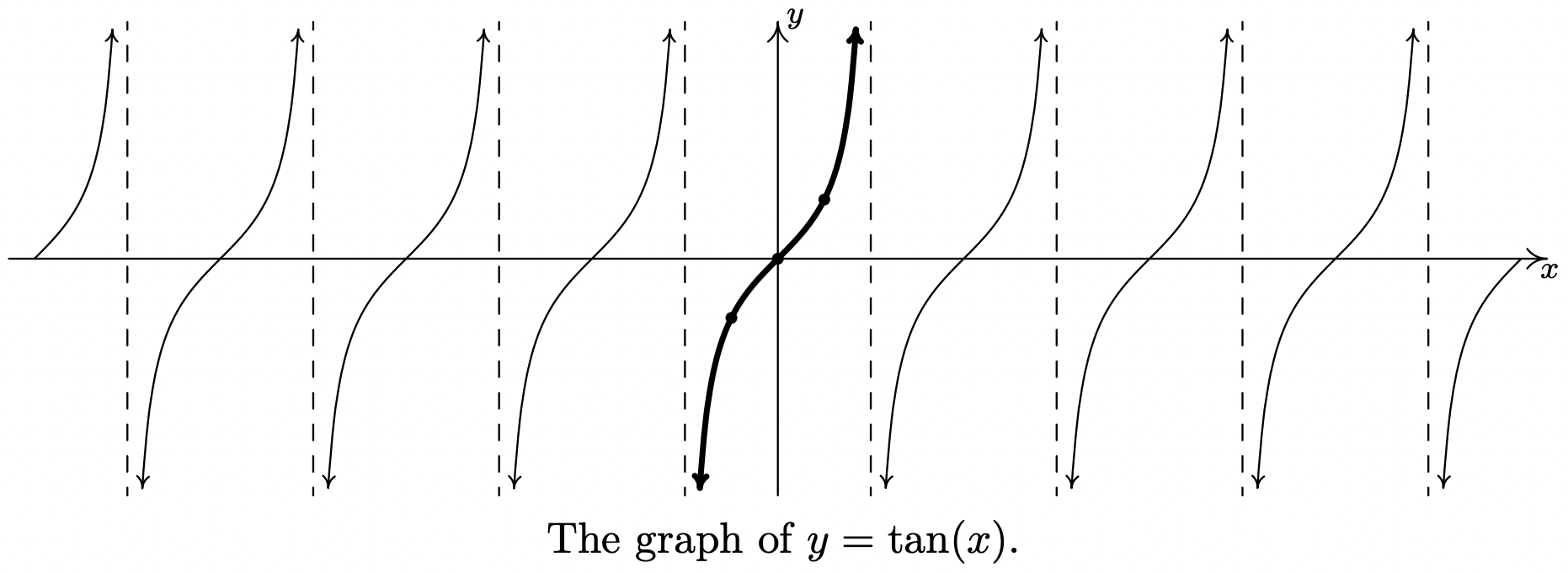
From the graph, it appears as if the tangent function is periodic with period \(\pi\). To prove that this is the case, we appeal to the sum formula for tangents. We have: \[\tan(x+\pi) = \dfrac{\tan(x) + \tan(\pi)}{1 - \tan(x) \tan(\pi)} = \dfrac{\tan(x) + 0}{1 - (\tan(x) )(0)} = \tan(x),\nonumber\]which tells us the period of \(\tan(x)\) is at most \(\pi\). To show that it is exactly \(\pi\), suppose \(p\) is a positive real number so that \(\tan(x+p) = \tan(x)\) for all real numbers \(x\). For \(x=0\), we have \(\tan(p) = \tan(0+p) = \tan(0) = 0\), which means \(p\) is a multiple of \(\pi\). The smallest positive multiple of \(\pi\) is \(\pi\) itself, so we have established the result. We take as our fundamental cycle for \(y=\tan(x)\) the interval \(\left[0, \pi \right] \), and use as our "quarter marks" \(x = 0\), \(\frac{\pi}{4}\), \(\frac{\pi}{2}\), \(\frac{3\pi}{4}\) and \(\pi\). Despite the tangent not being continuous over the interval, it is incredibly helpful for us to consider the fundamental cycle for the tangent function to be \( \left[ 0, \pi \right] \). From the graph, we see confirmation of our domain and range work in Section 10.3.

It should be no surprise that \(K(x) = \cot(x)\) behaves similarly to \(J(x) = \tan(x)\). Plotting \(\cot(x)\) over the interval \([0,2\pi]\) results in the graph below.

 

From these data, it clearly appears as if the period of \(\cot(x)\) is \(\pi\), and we leave it to the reader to prove this.¹³ We take as one fundamental cycle the interval \((0,\pi)\) with quarter marks: \(x= 0\), \(\frac{\pi}{4}\), \(\frac{\pi}{2}\), \(\frac{3\pi}{4}\) and \(\pi\). A more complete graph of \(y=\cot(x)\) is below, along with the fundamental cycle highlighted as usual. Once again, we see the domain and range of \(K(x) = \cot(x)\) as read from the graph matches with what we found analytically in Section 10.3.

The graph of \(y=\cot (x)\).

The properties of the tangent and cotangent functions are summarized below. Each of the results below can be traced back to properties of the cosine and sine functions and the definition of the tangent and cotangent functions as quotients thereof.

Theorem \(\PageIndex{4}\): Properties of the Tangent and Cotangent Functions

• The function \(J(x) = \tan(x)\)
  • has domain \(\left\{x: x \neq \frac{\pi}{2}+\pi k, k \text { is an integer }\right\}=\bigcup_{k=-\infty}^{\infty}\left(\frac{(2 k+1) \pi}{2}, \frac{(2 k+3) \pi}{2}\right)\)
  • has range \((-\infty, \infty)\)
  • is continuous and smooth on its domain
  • is odd
  • has period \(\pi\)
• The function \(K(x) = \cot(x)\)
  • has domain \(\{x: x \neq \pi k, k \text { is an integer }\}=\bigcup_{k=-\infty}^{\infty}(k \pi,(k+1) \pi)\)
  • has range \((-\infty, \infty)\)
  • is continuous and smooth on its domain
  • is odd
  • has period \(\pi\)

Subsection Footnotes

¹³ Certainly, mimicking the proof that the period of \(\tan (x)\) is an option; for another approach, consider transforming \(\tan (x)\) to \(\cot (x)\) using identities.

---

Transformations of the Tangent and Cotangent Functions

Before we dive into a set of examples showing how to graph transformations of the tangent and cotangent functions, it would be nice to know whether or not we can use Theorem \( \PageIndex{2} \). As mentioned previously (in the paragraph following Example \( \PageIndex{4} \)), only sinusoidal functions (i.e., the cosine and sine functions) have amplitude. Therefore, that aspect of Theorem \( \PageIndex{2} \) can be thrown out when graphing the tangent and cotangent functions. The period in Theorem \( \PageIndex{2} \) was compute as \[ \text{Period} = \dfrac{\text{Standard Period}}{B}, \nonumber \]and this formula still holds. You just have to remember that the standard period of both the tangent and cotangent is \( \pi \). Finally, when we compute the Step Size, we are going to evaluate the given tangent or cotangent function at the second and fourth points. This can be seen in the following example.

Example \( \PageIndex{5} \)

Graph one cycle of the following functions. Find the period.

1. \(f(x) = 1 - \tan\left(\frac{x}{2}\right)\).
2. \(g(x) = 2\cot\left(\frac{\pi}{2} x + \pi\right) + 1\).

Solution

1. We proceed as we have in all of the previous graphing examples by getting \( f(x) \) into a more "graphing-friendly" form:\[ f(x) = 1 - \tan{\left( \frac{x}{2} \right) } = - \tan{\left( \frac{1}{2} x \right)} + 1. \nonumber \]Reading this from left-to-right, we see the graph of the tangent will be reflected about the \( x\)-axis. Then we list all the other important information.\[ \begin{array}{rcccl}
   \text{Period} & = & \dfrac{\text{Standard Period}}{B} & = & \dfrac{\pi}{1/2} = 2\pi \\
   \text{Step Size} & = & \dfrac{\text{Period}}{4} & = & \dfrac{2\pi}{4} = \dfrac{\pi}{2} \\
   \text{Phase Shift} & = & -\dfrac{C}{B} & = & 0 \\
   \text{Midline Shift} & = & D & = & 1 \\
   \end{array} \nonumber \]As you can see, the process is almost the same as all the other examples in this section with the exception that the standard period of the tangent is \( \pi \) and the tangent does not have an amplitude. As per usual, we start by graphing the Midline.

   

   We then cleanly graph a fundamental cycle of an "upside down" tangent function.

   

   We now break our Midline into four equally-spaced subsections, starting at the beginning of the fundamental cycle and ending at the, well, end of the fundamental cycle.

   

   The first of these points is the Phase Shift. We label this and use the Step Size to label the other points.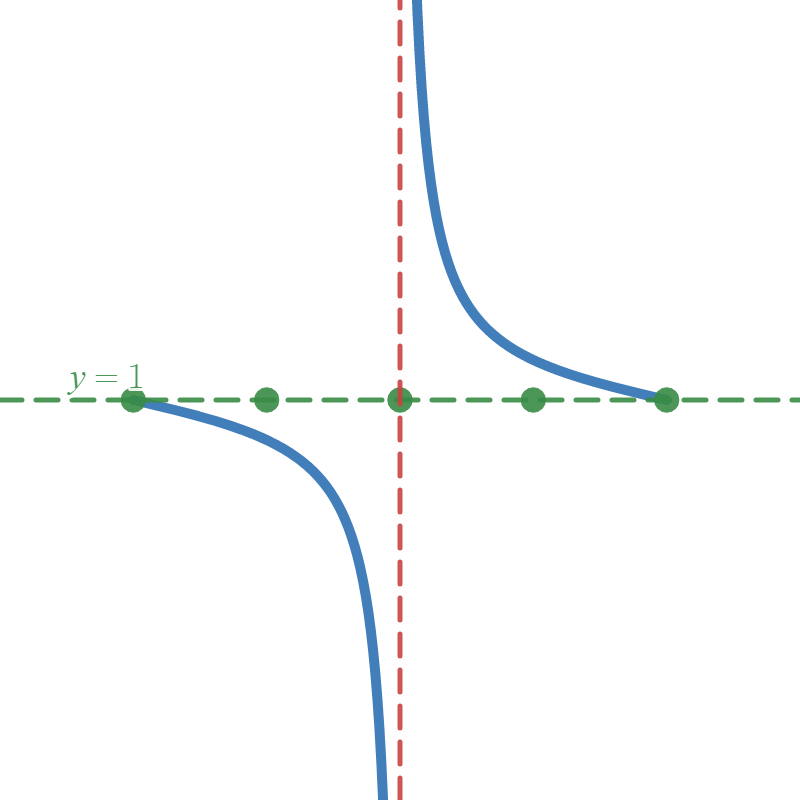

   

   We now have enough information to place the \( y \)-axis appropriately.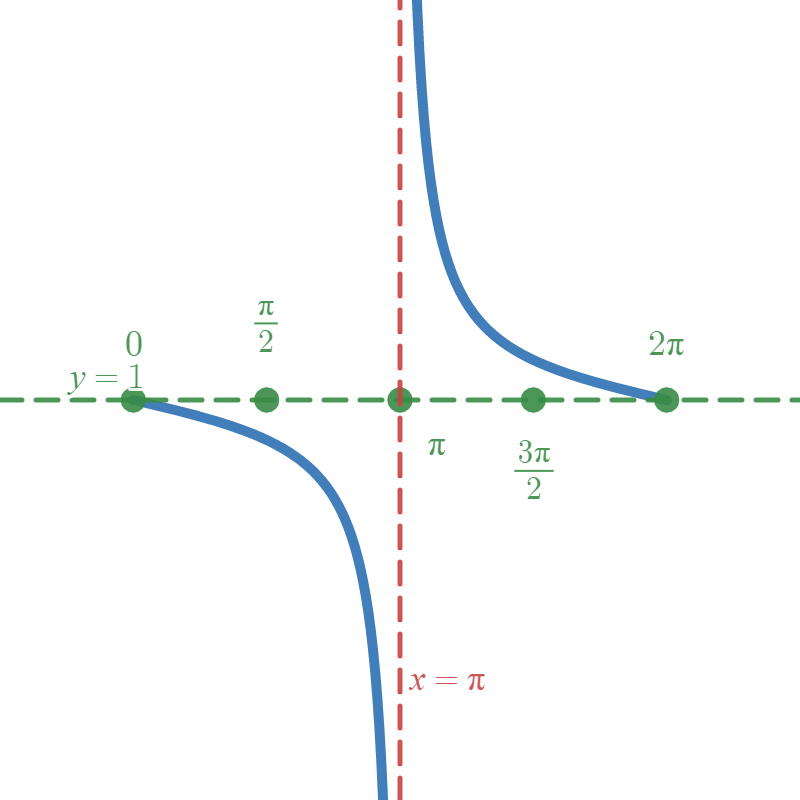

   

   Following that placement, we draw in the \( x \)-axis.

   

   A final "nice" step to perform is to label the function values for the second and fourth key points. This is very instructor-dependent, but I find it's a fast step and gives a little more detail for your graph. The second key point is at \( x = \frac{\pi}{2}\) and the fourth is at \( \frac{3 \pi}{2} \). Evaluating \(f\) at these values, we get \( f\left( \frac{\pi}{2} \right) = - \tan{\left( \frac{\pi}{4} \right)} + 1 = -1 + 1 = 0 \) and \( f\left( \frac{3\pi}{2} \right) = - \tan{\left( \frac{3\pi}{4} \right)} + 1 = -(-1) + 1 = 2 \).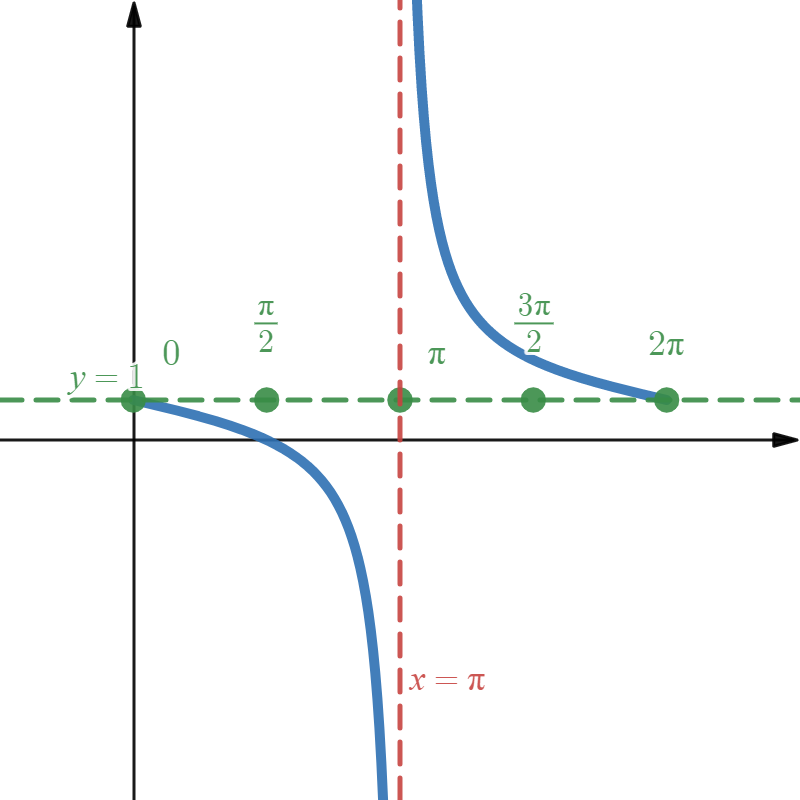

   

2. This time, we are going to put our "foot on the gas" and remove our step-by-step discussion.\[ g(x) = 2\cot\left(\frac{\pi}{2} x + \pi\right) + 1 = 2 \cot{\left(\frac{\pi}{2} \left(x + 2 \right) \right)} + 1 \nonumber \]\[ \begin{array}{rcccl}
   \text{Period} & = & \dfrac{\text{Standard Period}}{B} & = & \dfrac{\pi}{\pi/2} = 2 \\
   \text{Step Size} & = & \dfrac{\text{Period}}{4} & = & \dfrac{2}{4} = \dfrac{1}{2} \\
   \text{Phase Shift} & = & -\dfrac{C}{B} & = & -2 \\
   \text{Midline Shift} & = & D & = & 1 \\
   \end{array} \nonumber \]

        

   Placing the axes and evaluating \( g(-1.5) = 2 \cot{\left(\frac{\pi}{4}\right)} + 1 = 2 + 1 = 3 \) and \( g(-0.5) = 2 \cot{\left(\frac{3\pi}{4}\right)} + 1 = -2 + 1 = -1 \), we get