11.9E: Exercises

In Exercises 1 - 20, plot the set of parametric equations by hand. Be sure to indicate the orientation imparted on the curve by the parametrization.

1. $\left\{\begin{array}{l} x=4 t-3 \\ y=6 t-2 \end{array} \text { for } 0 \leq t \leq 1\right.$
2. $\left\{\begin{array}{l} x=4 t-1 \\ y=3-4 t \end{array} \text { for } 0 \leq t \leq 1\right.$
3. $\left\{\begin{array}{l} x=2 t \\ y=t^{2} \end{array} \text { for }-1 \leq t \leq 2\right.$
4. $\left\{\begin{array}{l} x=t-1 \\ y=3+2 t-t^{2} \end{array} \quad \text { for } 0 \leq t \leq 3\right.$
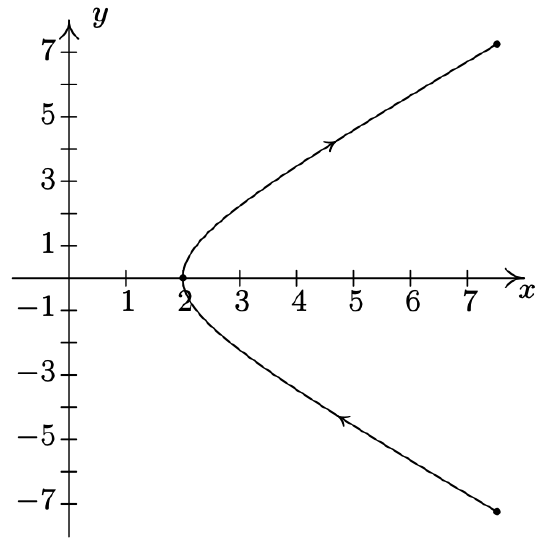
5. $\left\{\begin{array}{l} x=t^{2}+2 t+1 \\ y=t+1 \end{array} \text { for } t \leq 1\right.$
6. $\begin{cases}x=\frac{1}{9}\left(18-t^{2}\right) & \text { for } t \geq-3 \\ y=\frac{1}{3} t & \end{cases}$
7. $\left\{\begin{array}{l} x=t \\ y=t^{3} \end{array} \text { for }-\infty<t<\infty\right.$
8. $\left\{\begin{array}{l} x=t^{3} \\ y=t \end{array} \text { for }-\infty<t<\infty\right.$
9. $\left\{\begin{array}{l} x=\cos (t) \\ y=\sin (t) \end{array} \text { for }-\frac{\pi}{2} \leq t \leq \frac{\pi}{2}\right.$
10. $\left\{\begin{array}{l} x=3 \cos (t) \\ y=3 \sin (t) \end{array} \text { for } 0 \leq t \leq \pi\right.$
11. $\left\{\begin{array}{l} x=-1+3 \cos (t) \\ y=4 \sin (t) \end{array} \quad \text { for } 0 \leq t \leq 2 \pi\right.$
12. $\left\{\begin{array}{l} x=3 \cos (t) \\ y=2 \sin (t)+1 \end{array} \text { for } \frac{\pi}{2} \leq t \leq 2 \pi\right.$
13. $\left\{\begin{array}{l} x=2 \cos (t) \\ y=\sec (t) \end{array} \text { for } 0 \leq t<\frac{\pi}{2}\right.$
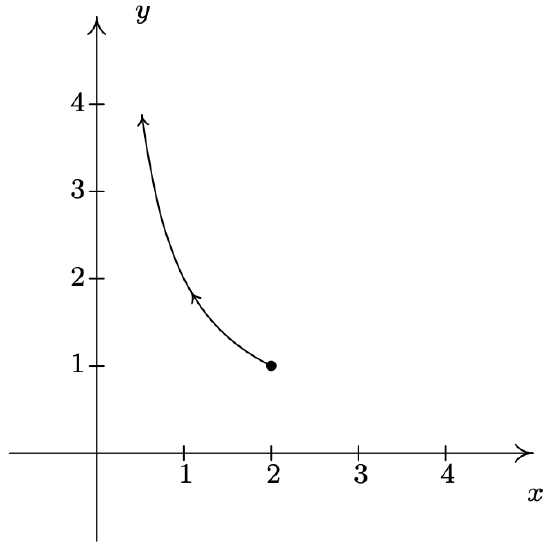
14. $\left\{\begin{array}{l} x=2 \tan (t) \\ y=\cot (t) \end{array} \text { for } 0<t<\frac{\pi}{2}\right.$
15. $\left\{\begin{array}{l} x=\sec (t) \\ y=\tan (t) \end{array} \text { for }-\frac{\pi}{2}<t<\frac{\pi}{2}\right.$
16. $\left\{\begin{array}{l} x=\sec (t) \\ y=\tan (t) \end{array} \text { for } \frac{\pi}{2}<t<\frac{3 \pi}{2}\right.$
17. $\left\{\begin{array}{l} x=\tan (t) \\ y=2 \sec (t) \end{array} \text { for }-\frac{\pi}{2}<t<\frac{\pi}{2}\right.$
18. $\left\{\begin{array}{l} x=\tan (t) \\ y=2 \sec (t) \end{array} \text { for } \frac{\pi}{2}<t<\frac{3 \pi}{2}\right.$
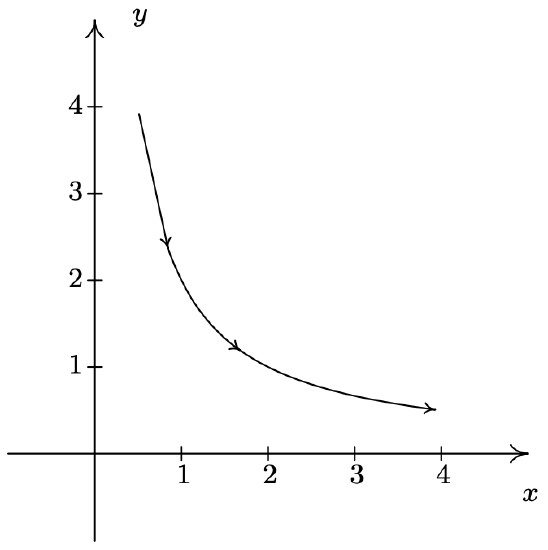
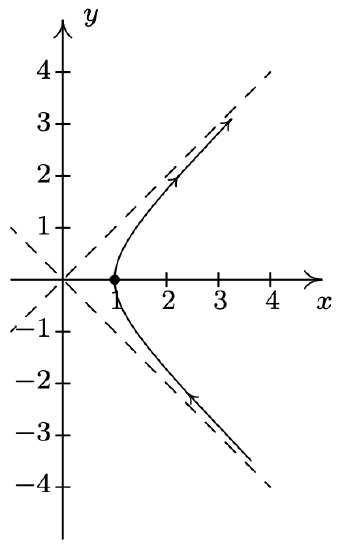
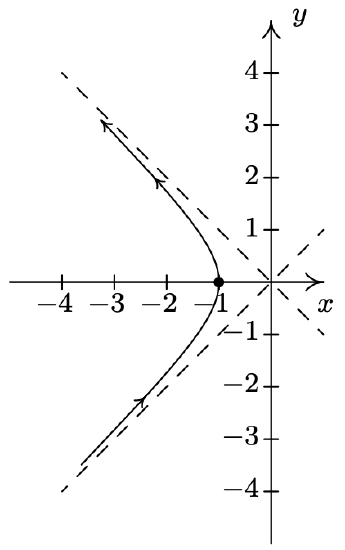
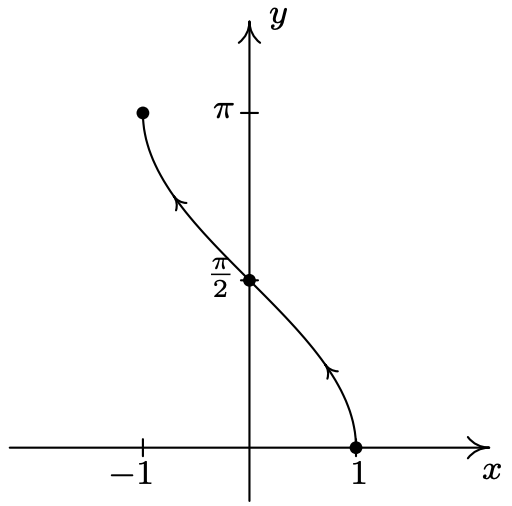
19. $\left\{\begin{array}{l} x=\cos (t) \\ y=t \end{array} \quad \text { for } 0 \leq t \leq \pi\right.$
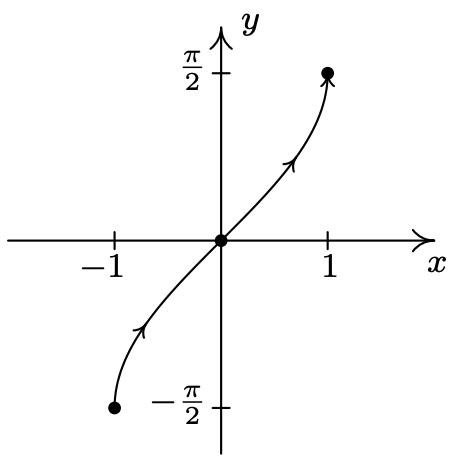
20. $\left\{\begin{array}{l} x=\sin (t) \\ y=t \end{array} \text { for }-\frac{\pi}{2} \leq t \leq \frac{\pi}{2}\right.$

In Exercises 21 - 24, plot the set of parametric equations with the help of a graphing utility. Be sure to indicate the orientation imparted on the curve by the parametrization.

21. $\left\{\begin{array}{l} x=t^{3}-3 t \\ y=t^{2}-4 \end{array} \text { for }-2 \leq t \leq 2\right.$
22. $\left\{\begin{array}{l} x=4 \cos ^{3}(t) \\ y=4 \sin ^{3}(t) \end{array} \text { for } 0 \leq t \leq 2 \pi\right.$
23. $\left\{\begin{array}{l} x=e^{t}+e^{-t} \\ y=e^{t}-e^{-t} \end{array} \text { for }-2 \leq t \leq 2\right.$
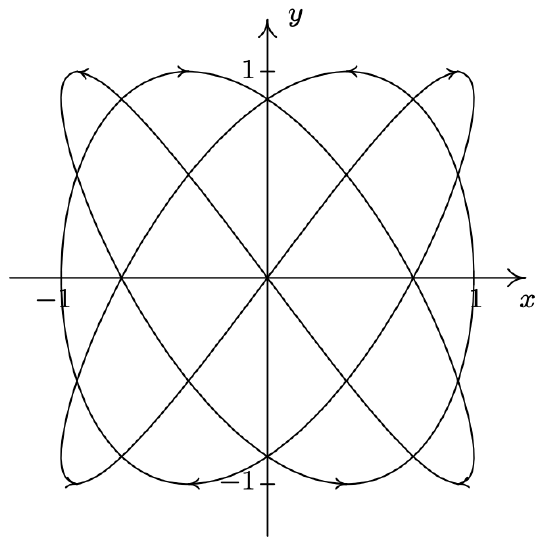
24. $\left\{\begin{array}{l} x=\cos (3 t) \\ y=\sin (4 t) \end{array} \text { for } 0 \leq t \leq 2 \pi\right.$

In Exercises 25 - 39, find a parametric description for the given oriented curve.

25. the directed line segment from (3, −5) to (−2, 2)
26. the directed line segment from (−2, −1) to (3, −4)
27. the curve $y=4-x^{2}$ from (−2, 0) to (2, 0).
28. the curve $y=4-x^{2}$ from (−2, 0) to (2, 0) (Shift the parameter so $t = 0$ corresponds to (−2, 0).)
29. the curve $x=y^{2}-9$ from (−5, −2) to (0, 3).
30. the curve $x=y^{2}-9$ from (0, 3) to (−5, −2). (Shift the parameter so $t = 0$ corresponds to (0, 3).)
31. the circle $x^{2}+y^{2}=25$, oriented counter-clockwise
32. the circle $(x-1)^{2}+y^{2}=4$, oriented counter-clockwise
33. the circle $x^{2}+y^{2}-6 y=0$, oriented counter-clockwise
34. the circle $x^{2}+y^{2}-6 y=0$, oriented clockwise

    (Shift the parameter so t begins at 0.)

35. the circle $(x-3)^{2}+(y+1)^{2}=117$, oriented counter-clockwise
36. the ellipse $(x-1)^{2}+9 y^{2}=9$, oriented counter-clockwise
37. the ellipse $9 x^{2}+4 y^{2}+24 y=0$, oriented counter-clockwise
38. the ellipse $9 x^{2}+4 y^{2}+24 y=0$, oriented clockwise (Shift the parameter so $t = 0$ corresponds to (0, 0).)
39. the triangle with vertices (0, 0), (3, 0), (0, 4), oriented counter-clockwise (Shift the parameter so t = 0 corresponds to (0, 0).)
40. Use parametric equations and a graphing utility to graph the inverse of $f(x)=x^{3}+3 x-4$.
41. Every polar curve $r=f(\theta)$ can be translated to a system of parametric equations with parameter $\theta$ by $\{x=r \cos (\theta)=f(\theta) \cos (\theta), y=r \sin (\theta)=f(\theta) \sin (\theta)$. Convert $r=6 \cos (2 \theta)$ to a system of parametric equations. Check your answer by graphing $r=6 \cos (2 \theta)$ by hand using the techniques presented in Section 11.5 and then graphing the parametric equations you found using a graphing utility.
42. Use your results from Exercises 3 and 4 in Section 11.1 to find the parametric equations which model a passenger’s position as they ride the London Eye.

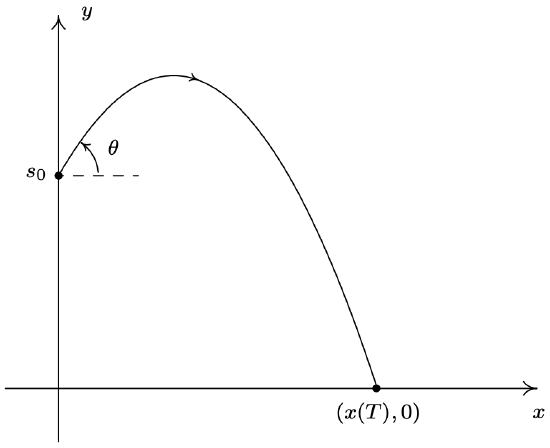
Suppose an object, called a projectile, is launched into the air. Ignoring everything except the force gravity, the path of the projectile is given by¹⁵

$$\left\{\begin{array}{l} x=v_{0} \cos (\theta) t \\ y=-\frac{1}{2} g t^{2}+v_{0} \sin (\theta) t+s_{0} \end{array} \quad \text { for } 0 \leq t \leq T\right.\nonumber$$

where $v_{0}$ is the initial speed of the object, $\theta$ is the angle from the horizontal at which the projectile is launched,¹⁶ $g$ is the acceleration due to gravity, $\mathcal{s}_{0}$ is the initial height of the projectile above the ground and $T$ is the time when the object returns to the ground. (See the figure below.)

43. Carl’s friend Jason competes in Highland Games Competitions across the country. In one event, the ‘hammer throw’, he throws a 56 pound weight for distance. If the weight is released 6 feet above the ground at an angle of $42^{\circ}$ with respect to the horizontal with an initial speed of 33 feet per second, find the parametric equations for the flight of the hammer. (Here, use $g=32 \frac{\mathrm{ft.}}{s^{2}}.$) When will the hammer hit the ground? How far away will it hit the ground? Check your answer using a graphing utility.
44. Eliminate the parameter in the equations for projectile motion to show that the path of the projectile follows the curve $$y=-\frac{g \sec ^{2}(\theta)}{2 v_{0}^{2}} x^{2}+\tan (\theta) x+s_{0}\nonumber$$ Use the vertex formula (Equation 2.4) to show the maximum height of the projectile is $$y=\frac{v_{0}^{2} \sin ^{2}(\theta)}{2 g}+s_{0} \quad \text { when } \quad x=\frac{v_{0}^{2} \sin (2 \theta)}{2 g}\nonumber$$
45. In another event, the ‘sheaf toss’, Jason throws a 20 pound weight for height. If the weight is released 5 feet above the ground at an angle of $85^{\circ}$ with respect to the horizontal and the sheaf reaches a maximum height of 31.5 feet, use your results from part 44 to determine how fast the sheaf was launched into the air. (Once again, use $g=32 \frac{\mathrm{ft.}}{s^{2}}.$)
46. Suppose $\theta=\frac{\pi}{2}$. (The projectile was launched vertically.) Simplify the general parametric formula given for $y(t)$ above using $g=9.8 \frac{\mathrm{m}}{\mathrm{s}^{2}}$ and compare that to the formula for $s(t)$ given in Exercise 25 in Section 2.3. What is $x(t)$ in this case?

In Exercises 47 - 52, we explore the hyperbolic cosine function, denoted $\cosh (t)$, and the hyperbolic sine function, denoted $\sinh(t)$, defined below:

$$\cosh (t)=\frac{e^{t}+e^{-t}}{2} \quad \text { and } \quad \sinh (t)=\frac{e^{t}-e^{-t}}{2}\nonumber$$

47. Using a graphing utility as needed, verify that the domain of $\cosh(t)$ is $(-\infty, \infty)$ and the range of $\cosh(t)$ is $[1, \infty)$.
48. Using a graphing utility as needed, verify that the domain and range of $\sinh(t)$ are both $(-\infty, \infty)$.
49. Show that $\{x(t)=\cosh (t), y(t)=\sinh (t)$ parametrize the right half of the ‘unit’ hyperbola $x^{2}-y^{2}=1$. (Hence the use of the adjective ‘hyperbolic.’)
50. Compare the definitions of $\cosh(t)$ and $\sinh(t)$ to the formulas for $\cos(t)$ and $\sin(t)$ given in Exercise 83f in Section 11.7.
51. Four other hyperbolic functions are waiting to be defined: the hyperbolic secant $\operatorname{sech}(t)$, the hyperbolic cosecant $\operatorname{csch}(t)$, the hyperbolic tangent $\tanh (t)$ and the hyperbolic cotangent $\operatorname{coth}(t)$. Define these functions in terms of $\cosh (t)$ and $\sinh (t)$, then convert them to formulas involving $e^{t}$ and $e^{-t}$. Consult a suitable reference (a Calculus book, or this entry on the hyperbolic functions) and spend some time reliving the thrills of trigonometry with these ‘hyperbolic’ functions.
52. If these functions look familiar, they should. Enjoy some nostalgia and revisit Exercise 35 in Section 6.5, Exercise 47 in Section 6.3 and the answer to Exercise 38 in Section 6.4.

11.10.2 Answers

1. $\left\{\begin{array}{l} x=4 t-3 \\ y=6 t-2 \end{array} \text { for } 0 \leq t \leq 1\right.$

   

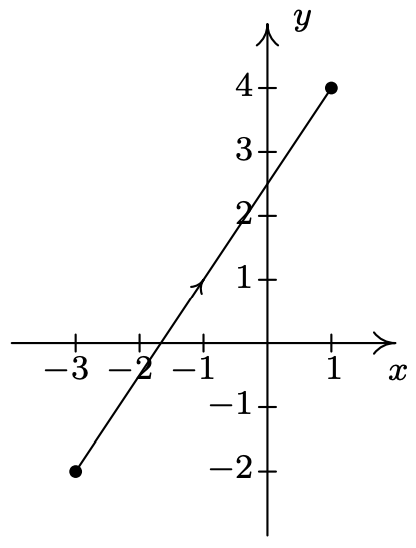
2. $\left\{\begin{array}{l} x=4 t-1 \\ y=3-4 t \end{array} \text { for } 0 \leq t \leq 1\right.$

   

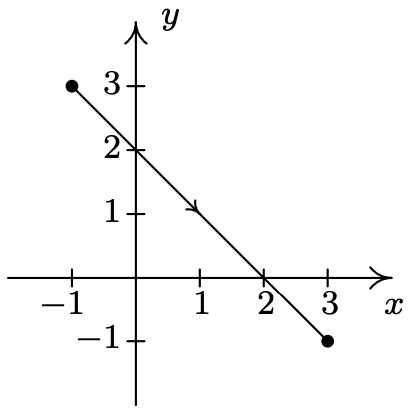
3. $\left\{\begin{array}{l} x=2 t \\ y=t^{2} \end{array} \text { for }-1 \leq t \leq 2\right.$

   

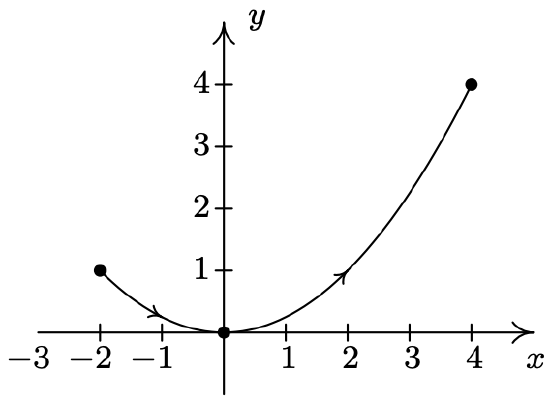
4. $\left\{\begin{array}{l} x=t-1 \\ y=3+2 t-t^{2} \end{array} \quad \text { for } 0 \leq t \leq 3\right.$

   

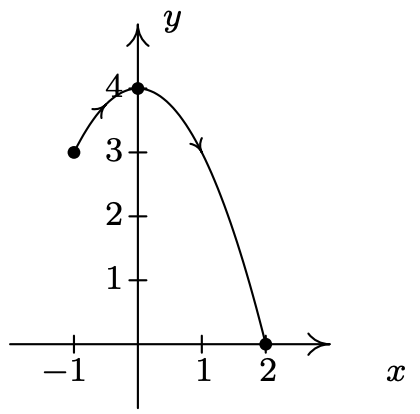
5. $\left\{\begin{array}{l} x=t^{2}+2 t+1 \\ y=t+1 \end{array} \text { for } t \leq 1\right.$

   

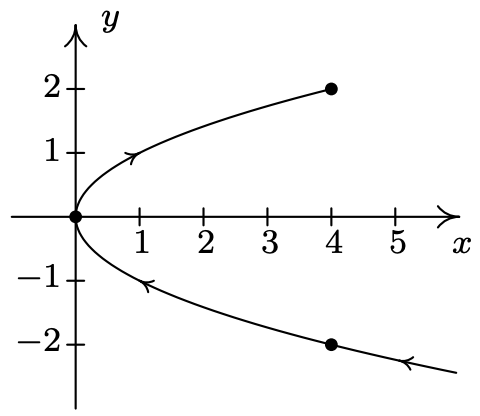
6. $\left\{\begin{array}{l} x=\frac{1}{9}\left(18-t^{2}\right) \\ y=\frac{1}{3} t \end{array} \text { for } t \geq-3\right.$

   

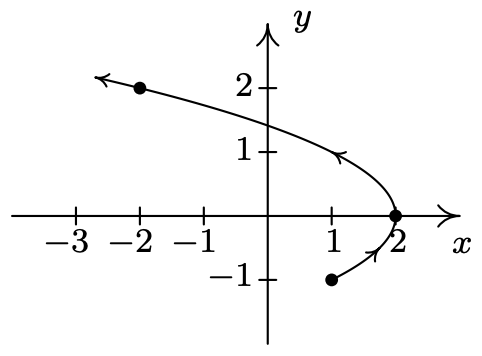
7. $\left\{\begin{array}{l} x=t \\ y=t^{3} \end{array} \text { for }-\infty<t<\infty\right.$

   

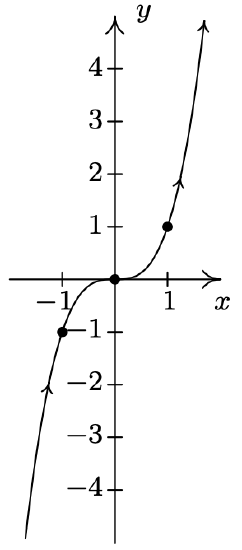
8. $\left\{\begin{array}{l} x=t^{3} \\ y=t \end{array} \quad \text { for }-\infty<t<\infty\right.$

   

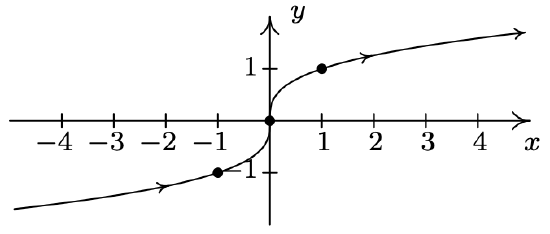
9. $\left\{\begin{array}{l} x=\cos (t) \\ y=\sin (t) \end{array} \text { for }-\frac{\pi}{2} \leq t \leq \frac{\pi}{2}\right.$

   

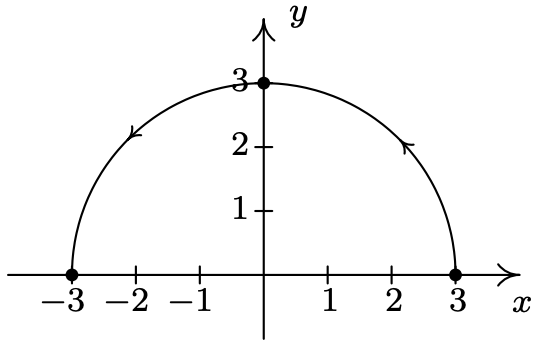
10. $\left\{\begin{array}{l} x=3 \cos (t) \\ y=3 \sin (t) \end{array} \text { for } 0 \leq t \leq \pi\right.$

    

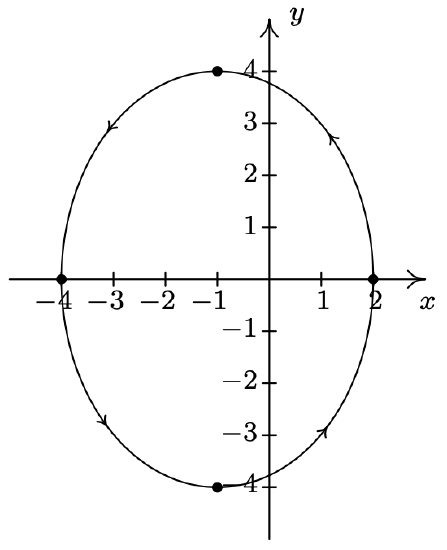
11. $\left\{\begin{array}{l} x=-1+3 \cos (t) \\ y=4 \sin (t) \end{array} \quad \text { for } 0 \leq t \leq 2 \pi\right.$

    

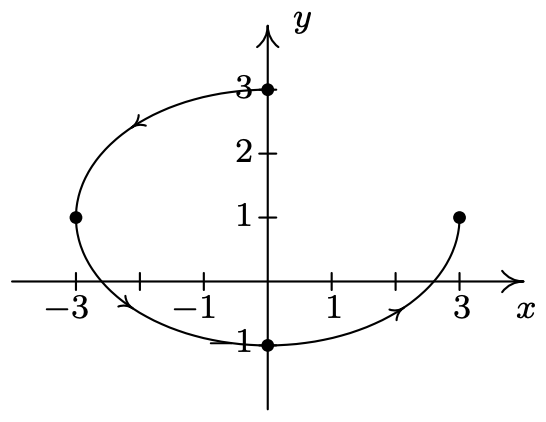
12. $\left\{\begin{array}{l} x=3 \cos (t) \\ y=2 \sin (t)+1 \end{array} \text { for } \frac{\pi}{2} \leq t \leq 2 \pi\right.$

    

13. $\left\{\begin{array}{l} x=2 \cos (t) \\ y=\sec (t) \end{array} \text { for } 0 \leq t<\frac{\pi}{2}\right.$

    

14. $\left\{\begin{array}{l} x=2 \tan (t) \\ y=\cot (t) \end{array} \text { for } 0<t<\frac{\pi}{2}\right.$

    

15. $\left\{\begin{array}{l} x=\sec (t) \\ y=\tan (t) \end{array} \text { for }-\frac{\pi}{2}<t<\frac{\pi}{2}\right.$

    

16. $\left\{\begin{array}{l} x=\sec (t) \\ y=\tan (t) \end{array} \text { for } \frac{\pi}{2}<t<\frac{3 \pi}{2}\right.$

    

17. $\left\{\begin{array}{l} x=\tan (t) \\ y=2 \sec (t) \end{array} \text { for }-\frac{\pi}{2}<t<\frac{\pi}{2}\right.$

    

18. $\left\{\begin{array}{l} x=\tan (t) \\ y=2 \sec (t) \end{array} \text { for } \frac{\pi}{2}<t<\frac{3 \pi}{2}\right.$

    

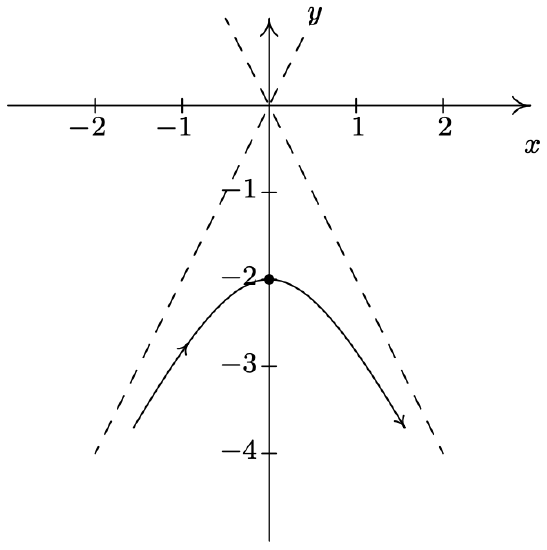
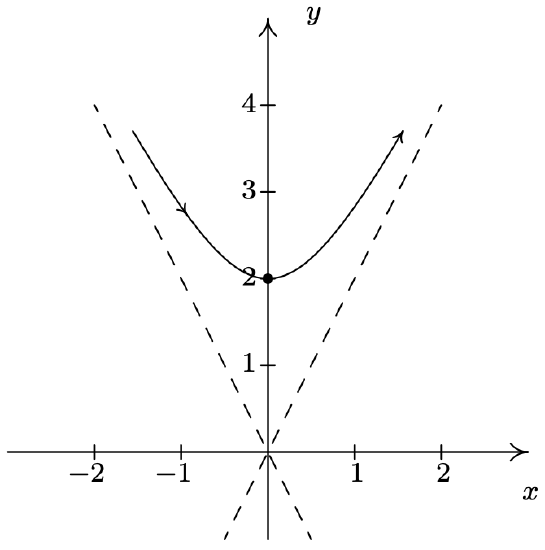
19. $\left\{\begin{array}{l} x=\cos (t) \\ y=t \end{array} \text { for } 0<t<\pi\right.$

    

20. $\left\{\begin{array}{l} x=\sin (t) \\ y=t \end{array} \text { for }-\frac{\pi}{2}<t<\frac{\pi}{2}\right.$

    

21. $\left\{\begin{array}{l} x=t^{3}-3 t \\ y=t^{2}-4 \end{array} \text { for }-2 \leq t \leq 2\right.$

    

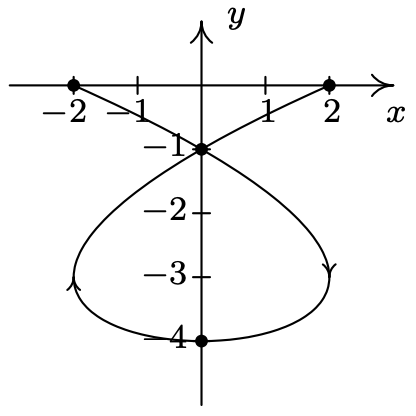
22. $\left\{\begin{array}{l} x=4 \cos ^{3}(t) \\ y=4 \sin ^{3}(t) \end{array} \text { for } 0 \leq t \leq 2 \pi\right.$

    

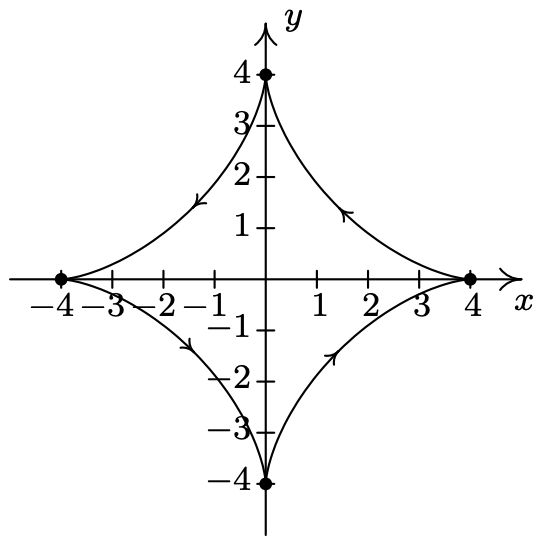
23. $\left\{\begin{array}{l} x=e^{t}+e^{-t} \\ y=e^{t}-e^{-t} \end{array} \quad \text { for }-2 \leq t \leq 2\right.$

    

24. $\left\{\begin{array}{l} x=\cos (3 t) \\ y=\sin (4 t) \end{array} \text { for } 0 \leq t \leq 2 \pi\right.$

    

25. $\left\{\begin{array}{l} x=3-5 t \\ y=-5+7 t \end{array} \text { for } 0 \leq t \leq 1\right.$
26. $\left\{\begin{array}{l} x=5 t-2 \\ y=-1-3 t \end{array} \text { for } 0 \leq t \leq 1\right.$
27. $\left\{\begin{array}{l} x=t \\ y=4-t^{2} \end{array} \text { for }-2 \leq t \leq 2\right.$
28. $\left\{\begin{array}{l} x=t-2 \\ y=4 t-t^{2} \end{array} \text { for } 0 \leq t \leq 4\right.$
29. $\left\{\begin{array}{l} x=t^{2}-9 \\ y=t \end{array} \text { for }-2 \leq t \leq 3\right.$
30. $\left\{\begin{array}{l} x=t^{2}-6 t \\ y=3-t \end{array} \quad \text { for } 0 \leq t \leq 5\right.$
31. $\left\{\begin{array}{l} x=5 \cos (t) \\ y=5 \sin (t) \end{array} \text { for } 0 \leq t<2 \pi\right.$
32. $\left\{\begin{array}{l} x=1+2 \cos (t) \\ y=2 \sin (t) \end{array} \text { for } 0 \leq t<2 \pi\right.$
33. $\left\{\begin{array}{l} x=3 \cos (t) \\ y=3+3 \sin (t) \end{array} \quad \text { for } 0 \leq t<2 \pi\right.$
34. $\left\{\begin{array}{l} x=3 \cos (t) \\ y=3-3 \sin (t) \end{array} \quad \text { for } 0 \leq t<2 \pi\right.$
35. $\left\{\begin{array}{l} x=3+\sqrt{117} \cos (t) \\ y=-1+\sqrt{117} \sin (t) \end{array} \text { for } 0 \leq t<2 \pi\right.$
36. $\left\{\begin{array}{l} x=1+3 \cos (t) \\ y=\sin (t) \end{array} \text { for } 0 \leq t<2 \pi\right.$
37. $\left\{\begin{array}{l} x=2 \cos (t) \\ y=3 \sin (t)-3 \end{array} \quad \text { for } 0 \leq t<2 \pi\right.$
38. $\left\{\begin{array}{l} x=2 \cos \left(t-\frac{\pi}{2}\right)=2 \sin (t) \\ y=-3-3 \sin \left(t-\frac{\pi}{2}\right)=-3+3 \cos (t) \end{array} \quad \text { for } 0 \leq t<2 \pi\right.$
39. $\{x(t), y(t) \text { where: }$ $$x(t)=\left\{\begin{array}{rl} 3 t, & 0 \leq t \leq 1 \\ 6-3 t, & 1 \leq t \leq 2 \\ 0, & 2 \leq t \leq 3 \end{array} \quad y(t)=\left\{\begin{aligned} 0, & 0 \leq t \leq 1 \\ 4 t-4, & 1 \leq t \leq 2 \\ 12-4 t, & 2 \leq t \leq 3 \end{aligned}\right.\right.\nonumber$$
40. The parametric equations for the inverse are $\left\{\begin{array}{l} x=t^{3}+3 t-4 \\ y=t \end{array} \text { for }-\infty<t<\infty\right.$
41. $r=6 \cos (2 \theta)$ translates to $\left\{\begin{array}{l} x=6 \cos (2 \theta) \cos (\theta) \\ y=6 \cos (2 \theta) \sin (\theta) \end{array} \text { for } 0 \leq \theta<2 \pi\right.$
42. The parametric equations which describe the locations of passengers on the London Eye are $$\left\{\begin{array}{l} x=67.5 \cos \left(\frac{\pi}{15} t-\frac{\pi}{2}\right)=67.5 \sin \left(\frac{\pi}{15} t\right) \\ y=67.5 \sin \left(\frac{\pi}{15} t-\frac{\pi}{2}\right)+67.5=67.5-67.5 \cos \left(\frac{\pi}{15} t\right) \end{array} \text { for }-\infty<t<\infty\right.\nonumber$$
43. The parametric equations for the hammer throw are $\left\{\begin{array}{l} x=33 \cos \left(42^{\circ}\right) t \\ y=-16 t^{2}+33 \sin \left(42^{\circ}\right) t+6 \end{array}\right.$ for $t \geq 0$. To find when the hammer hits the ground, we solve $y(t)=0$ and get $t \approx-0.23$ or 1.61. Since $t \geq 0$, the hammer hits the ground after approximately $t = 1.61$ seconds after it was launched into the air. To find how far away the hammer hits the ground, we find $x(1.61) \approx 39.48$ feet from where it was thrown into the air.
44. We solve $y=\frac{v_{0}^{2} \sin ^{2}(\theta)}{2 g}+s_{0}=\frac{v_{0}^{2} \sin ^{2}\left(85^{\circ}\right)}{2(32)}+5=31.5$ to get $v_{0}=\pm 41.34$. The initial speed of the sheaf was approximately 41.34 feet per second.