2.10: Prime Factorization and the Least Common Multiple (Part 2)
- Page ID
- 21676
( \newcommand{\kernel}{\mathrm{null}\,}\)
Find the Least Common Multiple (LCM) of Two Numbers
One of the reasons we look at multiples and primes is to use these techniques to find the least common multiple of two numbers. This will be useful when we add and subtract fractions with different denominators.
Listing Multiples Method
A common multiple of two numbers is a number that is a multiple of both numbers. Suppose we want to find common multiples of 10 and 25. We can list the first several multiples of each number. Then we look for multiples that are common to both lists—these are the common multiples.
10:10,20,30,40,50,60,70,80,90,100,110,…25:25,50,75,100,125,…
We see that 50 and 100 appear in both lists. They are common multiples of 10 and 25. We would find more common multiples if we continued the list of multiples for each.
The smallest number that is a multiple of two numbers is called the least common multiple (LCM). So the least LCM of 10 and 25 is 50.
HOW TO: FIND THE LEAST COMMON MULTIPLE (LCM) OF TWO NUMBERS BY LISTING MULTIPLES
Step 1. List the first several multiples of each number.
Step 2. Look for multiples common to both lists. If there are no common multiples in the lists, write out additional multiples for each number.
Step 3. Look for the smallest number that is common to both lists.
Step 4. This number is the LCM.
Example 2.10.5: lcm
Find the LCM of 15 and 20 by listing multiples.
Solution
List the first several multiples of 15 and of 20. Identify the first common multiple.
15:15,30,45,60,75,90,105,12020:20,40,60,80,100,120,140,160
The smallest number to appear on both lists is 60, so 60 is the least common multiple of 15 and 20. Notice that 120 is on both lists, too. It is a common multiple, but it is not the least common multiple.
Exercise 2.10.9
Find the least common multiple (LCM) of the given numbers: 9 and 12
- Answer
-
36
Exercise 2.10.10
Find the least common multiple (LCM) of the given numbers: 18 and 24
- Answer
-
72
Prime Factors Method
Another way to find the least common multiple of two numbers is to use their prime factors. We’ll use this method to find the LCM of 12 and 18.
We start by finding the prime factorization of each number.
12=2⋅2⋅318=2⋅3⋅3
Then we write each number as a product of primes, matching primes vertically when possible.
12=2⋅2⋅318=2⋅3⋅3
Now we bring down the primes in each column. The LCM is the product of these factors.
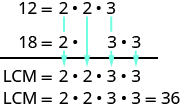
Notice that the prime factors of 12 and the prime factors of 18 are included in the LCM. By matching up the common primes, each common prime factor is used only once. This ensures that 36 is the least common multiple.
HOW TO: FIND THE LCM USING THE PRIME FACTORS METHOD
Step 1. Find the prime factorization of each number.
Step 2. Write each number as a product of primes, matching primes vertically when possible.
Step 3. Bring down the primes in each column.
Step 4. Multiply the factors to get the LCM.
Example 2.10.6: lcm
Find the LCM of 15 and 18 using the prime factors method.
Solution
| Write each number as a product of primes. | 15=3⋅518=2⋅3⋅3 |
| Write each number as a product of primes, matching primes vertically when possible. | 15=3⋅518=2⋅3⋅3 |
| Bring down the primes in each column. | 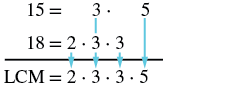 |
| Multiply the factors to get the LCM. |
LCM = 2 • 3 • 3 • 5 The LCM of 15 and 18 is 90. |
Exercise 2.10.11
Find the LCM using the prime factors method: 15 and 20
- Answer
-
60
Exercise 2.10.12
Find the LCM using the prime factors method: 15 and 35
- Answer
-
105
Example 2.10.7: lcm
Find the LCM of 50 and 100 using the prime factors method.
Solution
| Write the prime factorization of each number. | 50=2⋅5⋅5100=2⋅2⋅5⋅5 |
| Write each number as a product of primes, matching primes vertically when possible. | 50=2⋅5⋅5100=2⋅2⋅5⋅5 |
| Bring down the primes in each column. | 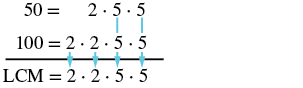 |
| Multiply the factors to get the LCM. |
LCM = 2 • 2 • 5 • 5 The LCM of 50 and 100 is 100. |
Exercise 2.10.13
Find the LCM using the prime factors method: 55,88
- Answer
-
440
Exercise 2.10.14
Find the LCM using the prime factors method: 60,72
- Answer
-
360
Access Additional Online Resources
- Ex 1: Prime Factorization
- Ex 2: Prime Factorization
- Ex 3: Prime Factorization
- Ex 1: Prime Factorization Using Stacked Division
- Ex 2: Prime Factorization Using Stacked Division
- The Least Common Multiple
- Example: Determining the Least Common Multiple Using a List of Multiples
- Example: Determining the Least Common Multiple Using Prime Factorization
Key Concepts
- Find the prime factorization of a composite number using the tree method.
- Find any factor pair of the given number, and use these numbers to create two branches.
- If a factor is prime, that branch is complete. Circle the prime.
- If a factor is not prime, write it as the product of a factor pair and continue the process.
- Write the composite number as the product of all the circled primes.
- Find the prime factorization of a composite number using the ladder method.
- Divide the number by the smallest prime.
- Continue dividing by that prime until it no longer divides evenly.
- Divide by the next prime until it no longer divides evenly.
- Continue until the quotient is a prime.
- Write the composite number as the product of all the primes on the sides and top of the ladder.
- Find the LCM by listing multiples.
- List the first several multiples of each number.
- Look for multiples common to both lists. If there are no common multiples in the lists, write out additional multiples for each number.
- Look for the smallest number that is common to both lists.
- This number is the LCM.
- Find the LCM using the prime factors method.
- Find the prime factorization of each number.
- Write each number as a product of primes, matching primes vertically when possible.
- Bring down the primes in each column.
- Multiply the factors to get the LCM.
Glossary
- least common multiple
-
The smallest number that is a multiple of two numbers is called the least common multiple (LCM).
- prime factorization
-
The prime factorization of a number is the product of prime numbers that equals the number.
Practice Makes Perfect
Find the Prime Factorization of a Composite Number
In the following exercises, find the prime factorization of each number using the factor tree method.
- 86
- 78
- 132
- 455
- 693
- 420
- 115
- 225
- 2475
- 1560
In the following exercises, find the prime factorization of each number using the ladder method.
- 56
- 72
- 168
- 252
- 391
- 400
- 432
- 627
- 2160
- 2520
In the following exercises, find the prime factorization of each number using any method.
- 150
- 180
- 525
- 444
- 36
- 50
- 350
- 144
Find the Least Common Multiple (LCM) of Two Numbers
In the following exercises, find the least common multiple (LCM) by listing multiples.
- 8, 12
- 4, 3
- 6, 15
- 12, 16
- 30, 40
- 20, 30
- 60, 75
- 44, 55
In the following exercises, find the least common multiple (LCM) by using the prime factors method.
- 8, 12
- 12, 16
- 24, 30
- 28, 40
- 70, 84
- 84, 90
In the following exercises, find the least common multiple (LCM) using any method.
- 6, 21
- 9, 15
- 24, 30
- 32, 40
Everyday Math
- Grocery shopping Hot dogs are sold in packages of ten, but hot dog buns come in packs of eight. What is the smallest number of hot dogs and buns that can be purchased if you want to have the same number of hot dogs and buns? (Hint: it is the LCM!)
- Grocery shopping Paper plates are sold in packages of 12 and party cups come in packs of 8. What is the smallest number of plates and cups you can purchase if you want to have the same number of each? (Hint: it is the LCM!)
Writing Exercises
- Do you prefer to find the prime factorization of a composite number by using the factor tree method or the ladder method? Why?
- Do you prefer to find the LCM by listing multiples or by using the prime factors method? Why?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


