3.1: Introduction to Integers (Part 1)
- Last updated
- Jul 2, 2019
- Save as PDF
- Page ID
- 21680
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Locate positive and negative numbers on the number line
- Order positive and negative numbers
- Find opposites
- Simplify expressions with absolute value
- Translate word phrases to expressions with integers
be prepared!
Before you get started, take this readiness quiz.
- Plot 0, 1, and 3 on a number line. If you missed this problem, review Example 1.1.1.
- Fill in the appropriate symbol: (=, <, or > ): 2___4 If you missed this problem, review Example 2.1.2.
Locate Positive and Negative Numbers on the Number Line
Do you live in a place that has very cold winters? Have you ever experienced a temperature below zero? If so, you are already familiar with negative numbers. A negative number is a number that is less than 0. Very cold temperatures are measured in degrees below zero and can be described by negative numbers. For example, −1∘ F (read as “negative one degree Fahrenheit”) is 1 degree below 0. A minus sign is shown before a number to indicate that it is negative. Figure 3.1.1 shows −20∘ F, which is 20 degrees below 0.

Figure 3.1.1: Temperatures below zero are described by negative numbers.
Temperatures are not the only negative numbers. A bank overdraft is another example of a negative number. If a person writes a check for more than he has in his account, his balance will be negative.
Elevations can also be represented by negative numbers. The elevation at sea level is 0 feet. Elevations above sea level are positive and elevations below sea level are negative. The elevation of the Dead Sea, which borders Israel and Jordan, is about 1,302 feet below sea level, so the elevation of the Dead Sea can be represented as −1,302 feet. See Figure 3.1.2.
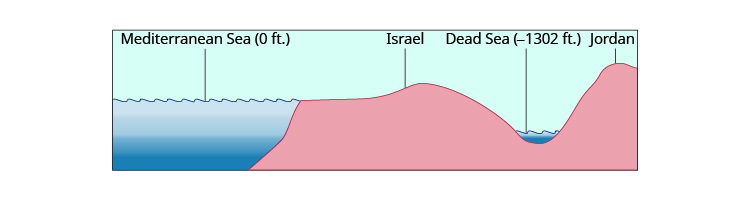
Figure 3.1.2: The surface of the Mediterranean Sea has an elevation of 0 ft. The diagram shows that nearby mountains have higher (positive) elevations whereas the Dead Sea has a lower (negative) elevation.
Depths below the ocean surface are also described by negative numbers. A submarine, for example, might descend to a depth of 500 feet. Its position would then be −500 feet as labeled in Figure 3.1.3.
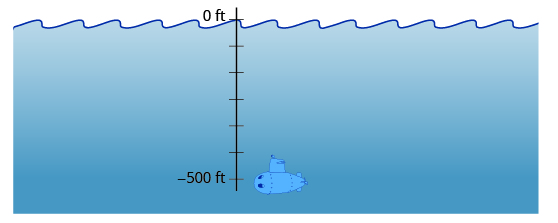
Figure 3.1.3: Depths below sea level are described by negative numbers. A submarine 500 ft below sea level is at −500 ft.
Both positive and negative numbers can be represented on a number line. Recall that the number line created in Add Whole Numbers started at 0 and showed the counting numbers increasing to the right as shown in Figure 3.1.4. The counting numbers (1,2,3,…) on the number line are all positive. We could write a plus sign, +, before a positive number such as +2 or +3, but it is customary to omit the plus sign and write only the number. If there is no sign, the number is assumed to be positive.

Figure 3.1.4
Now we need to extend the number line to include negative numbers. We mark several units to the left of zero, keeping the intervals the same width as those on the positive side. We label the marks with negative numbers, starting with −1 at the first mark to the left of 0,−2 at the next mark, and so on. See Figure 3.1.5.
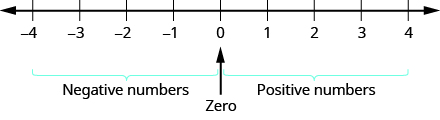
Figure 3.1.5: On a number line, positive numbers are to the right of zero. Negative numbers are to the left of zero. What about zero? Zero is neither positive nor negative.
The arrows at either end of the line indicate that the number line extends forever in each direction. There is no greatest positive number and there is no smallest negative number.
Example 3.1.1: plot on the number line
Plot the numbers on a number line:
- 3
- −3
- −2
Solution
Draw a number line. Mark 0 in the center and label several units to the left and right.
- To plot 3, start at 0 and count three units to the right. Place a point as shown in Figure 3.1.6.

Figure 3.1.6
- To plot −3, start at 0 and count three units to the left. Place a point as shown in Figure 3.1.7.

Figure 3.1.7
- To plot −2, start at 0 and count two units to the left. Place a point as shown in Figure 3.1.8.

Figure 3.1.8
Exercise 3.1.1
Plot the numbers on a number line.
1, −1, −4
- Answer
-
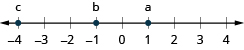
Exercise 3.1.2
Plot the numbers on a number line.
−4, 4, −1
- Answer
-
Order Positive and Negative Numbers
We can use the number line to compare and order positive and negative numbers. Going from left to right, numbers increase in value. Going from right to left, numbers decrease in value. See Figure 3.1.9.
Figure 3.1.9
Just as we did with positive numbers, we can use inequality symbols to show the ordering of positive and negative numbers. Remember that we use the notation a<b (read a is less than b) when a is to the left of b on the number line. We write a>b (read a is greater than b) when a is to the right of b on the number line. This is shown for the numbers 3 and 5 in Figure 3.1.10.
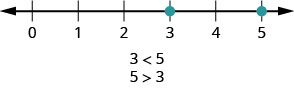
Figure 3.1.10: The number 3 is to the left of 5 on the number line. So 3 is less than 5, and 5 is greater than 3.
The numbers lines to follow show a few more examples.
4 is to the right of 1 on the number line, so 4>1. 1 is to the left of 4 on the number line, so 1<4.
−2 is to the left of 1 on the number line, so −2<1. 1 is to the right of −2 on the number line, so 1>−2.
−1 is to the right of −3 on the number line, so −1>−3. −3 is to the left of −1 on the number line, so −3<−1.
Example 3.1.2: order the pairs
Order each of the following pairs of numbers using < or >:
- 14___6
- −1___9
- −1___−4
- 2___−20
Solution
Begin by plotting the numbers on a number line as shown in Figure 3.1.11.

Figure 3.1.11
| Compare 14 and 6. | 14___6 |
| 14 is to the right of 6 on the number line. | 14 > 6 |
| Compare −1 and 9. | −1___9 |
| −1 is to the left of 9 on the number line. | −1 < 9 |
| Compare −1 and −4. | −1___−4 |
| −1 is to the right of −4 on the number line. | −1 > −4 |
| Compare 2 and −20. | 2___−20 |
| 2 is to the right of −20 on the number line. | 2 > −20 |
Exercise 3.1.3
Order each of the following pairs of numbers using < or >.
- 15___7
- −2___5
- −3___−7
- 5___−17
- Answer a
-
>
- Answer b
-
<
- Answer c
-
>
- Answer d
-
>
Exercise 3.1.4
Order each of the following pairs of numbers using < or >.
- 8___13
- 3___−4
- −5___−2
- 9___−21
- Answer a
-
<
- Answer b
-
>
- Answer c
-
<
- Answer d
-
>
Find Opposites
On the number line, the negative numbers are a mirror image of the positive numbers with zero in the middle. Because the numbers 2 and −2 are the same distance from zero, they are called opposites. The opposite of 2 is −2, and the opposite of −2 is 2 as shown in Figure 3.1.12a. Similarly, 3 and −3 are opposites as shown in Figure 3.1.12b.
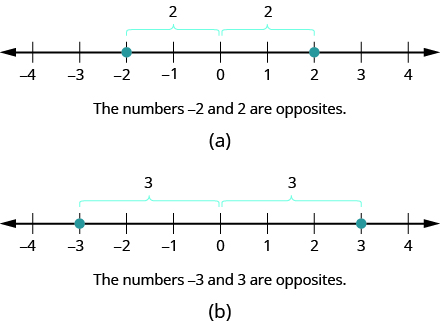
Figure 3.1.12
Definition: opposite
The opposite of a number is the number that is the same distance from zero on the number line, but on the opposite side of zero.
Example 3.1.3:
Find the opposite of each number:
- 7
- −10
Solution
- The number −7 is the same distance from 0 as 7, but on the opposite side of 0. So −7 is the opposite of 7 as shown in Figure 3.1.13.

Figure 3.1.13
- The number 10 is the same distance from 0 as −10, but on the opposite side of 0. So 10 is the opposite of −10 as shown in Figure 3.1.14.

Figure 3.1.14
Exercise 3.1.5
Find the opposite of each number:
- 4
- −3
- Answer a
-
−4
- Answer b
-
3
Exercise 3.1.6
Find the opposite of each number:
- 8
- −5
- Answer a
-
−8
- Answer b
-
5
Opposite Notation
Just as the same word in English can have different meanings, the same symbol in algebra can have different meanings.
The specific meaning becomes clear by looking at how it is used. You have seen the symbol “−”, in three different ways.
| 10 - 4 |
Between two numbers, the symbol indicates the operation of subtraction. We read 10 − 4 as 10 minus 4. |
| -8 |
In front of a number, the symbol indicates a negative number. We read −8 as negative eight. |
| -x |
In front of a variable or a number, it indicates the opposite. We read −x as the opposite of x . |
| − (−2) |
Here we have two signs. The sign in the parentheses indicates that the number is negative 2. The sign outside the parentheses indicates the opposite. We read − (−2) as the opposite of −2. |
Definition: Opposite Notation
−a means the opposite of the number a.
The notation −a is read the opposite of a.
Example 3.1.4: simplify
Simplify: −(−6).
Solution
| −(−6) | |
| The opposite of −6 is 6. | 6 |
Exercise 3.1.7
Simplify: −(−1)
- Answer
-
1
Exercise 3.1.8
Simplify: −(−5)
- Answer
-
5
Integers
The set of counting numbers, their opposites, and 0 is the set of integers.
Definition: integers
Integers are counting numbers, their opposites, and zero.
…−3,−2,−1,0,1,2,3…
We must be very careful with the signs when evaluating the opposite of a variable.
Example 3.1.5: evaluate
Evaluate −x:
- when x=8
- when x=−8
Solution
| To evaluate −x when x = 8, substitute 8 for x. | −x |
| Substitute 8 for x. | −(8) |
| Simplify. | −8 |
| To evaluate −x when x = −8, substitute 8 for x. | −x |
| Substitute −8 for x. | −(−8) |
| Simplify. | −8 |
Exercise 3.1.9
Evaluate −n:
- when n=4
- when n=−4
- Answer a
-
−4
- Answer b
-
4
Exercise 3.1.10
Evaluate −m:
- when m=11
- when m=−11
- Answer a
-
−11
- Answer b
-
11
Simplify Expressions with Absolute Value
We saw that numbers such as 5 and −5 are opposites because they are the same distance from 0 on the number line. They are both five units from 0. The distance between 0 and any number on the number line is called the absolute value of that number. Because distance is never negative, the absolute value of any number is never negative. The symbol for absolute value is two vertical lines on either side of a number. So the absolute value of 5 is written as |5|, and the absolute value of −5 is written as |−5| as shown in Figure 3.1.15.
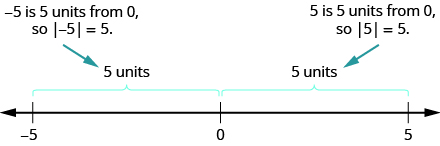
Figure 3.1.15
Definition: Absolute Value
The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number n is written as |n|.
|n|≥0forallnumbers
Example 3.6:
Simplify:
- |3|
- |−44|
- |0|
Solution
| |3| | |
| 3 is 3 units from zero. | 3 |
| |-44| | |
| -44 is 44 units from zero. | 44 |
| |0| | |
| 0 is already at zero. | 0 |
Exercise 3.1.11
Simplify:
- |12|
- −|−28|
- Answer a
-
12
- Answer b
-
−28
Exercise 3.12:
Simplify:
- |9|
- −|37|
- Answer a
-
9
- Answer b
-
−37
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.





