5.6: Decimals and Fractions (Part 2)
- Last updated
- Jul 2, 2019
- Save as PDF
- Page ID
- 21714
( \newcommand{\kernel}{\mathrm{null}\,}\)
Find the Circumference and Area of Circles
The properties of circles have been studied for over 2,000 years. All circles have exactly the same shape, but their sizes are affected by the length of the radius, a line segment from the center to any point on the circle. A line segment that passes through a circle’s center connecting two points on the circle is called a diameter. The diameter is twice as long as the radius. See Figure 5.6.1.
The size of a circle can be measured in two ways. The distance around a circle is called its circumference.
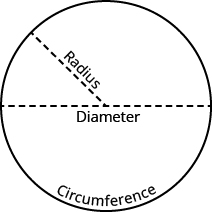
Figure 5.6.1
Archimedes discovered that for circles of all different sizes, dividing the circumference by the diameter always gives the same number. The value of this number is pi, symbolized by Greek letter π (pronounced pie). However, the exact value of π cannot be calculated since the decimal never ends or repeats (we will learn more about numbers like this in The Properties of Real Numbers.)
If we want the exact circumference or area of a circle, we leave the symbol π in the answer. We can get an approximate answer by substituting 3.14 as the value of π. We use the symbol ≈ to show that the result is approximate, not exact.
Note: Properties of Circles
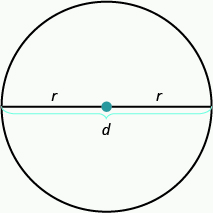
r is the length of the radius.
d is the length of the diameter.
The circumference is 2πr.C=2πr
The area is πr2.A=πr2
Since the diameter is twice the radius, another way to find the circumference is to use the formula C = πd.
Suppose we want to find the exact area of a circle of radius 10 inches. To calculate the area, we would evaluate the formula for the area when r = 10 inches and leave the answer in terms of π.
A=πr2A=π(102)A=π⋅100
We write π after the 100. So the exact value of the area is A = 100π square inches. To approximate the area, we would substitute π ≈ 3.14.
A=100π≈100⋅3.14≈314squareinches
Remember to use square units, such as square inches, when you calculate the area.
Example 5.6.10:
A circle has radius 10 centimeters. Approximate its (a) circumference and (b) area.
Solution
(a) Find the circumference when r = 10.
| Write the formula for circumference. | C = 2πr |
| Substitute 3.14 for π and 10 for r. | C ≈ 2(3.14)(10) |
| Multiply. | C ≈ 62.8 centimeters |
(b) Find the area when r = 10.
| Write the formula for area. | A = πr2 |
| Substitute 3.14 for π and 10 for r. | A ≈ (3.14)(10)2 |
| Multiply. | A ≈ 314 square centimeters |
Exercise 5.6.19:
A circle has radius 50 inches. Approximate its (a) circumference and (b) area.
- Answer a
-
314 in.
- Answer b
-
7850 sq. in.
Exercise 5.6.20:
A circle has radius 100 feet. Approximate its (a) circumference and (b) area.
- Answer a
-
628 ft.
- Answer b
-
31,400 sq. ft.
Example 5.6.11:
A circle has radius 42.5 centimeters. Approximate its (a) circumference and (b) area.
Solution
(a) Find the circumference when r = 42.5.
| Write the formula for circumference. | C = 2πr |
| Substitute 3.14 for π and 42.5 for r. | C ≈ 2(3.14)(42.5) |
| Multiply. | C ≈ 266.9 centimeters |
(b) Find the area when r = 42.5.
| Write the formula for area. | A = πr2 |
| Substitute 3.14 for π and 42.5 for r. | A ≈ (3.14)(42.5)2 |
| Multiply. | A ≈ 5671.625 square centimeters |
Exercise 5.6.21:
A circle has radius 51.8 centimeters. Approximate its (a) circumference and (b) area.
- Answer a
-
325.304 cm
- Answer b
-
8425.3736 sq. cm
Exercise 5.6.22:
A circle has radius 26.4 meters. Approximate its (a) circumference and (b) area.
- Answer a
-
165.792 m
- Answer b
-
2188.4544 sq. m
Approximate π with a Fraction
Convert the fraction 227 to a decimal. If you use your calculator, the decimal number will fill up the display and show 3.14285714. But if we round that number to two decimal places, we get 3.14, the decimal approximation of π. When we have a circle with radius given as a fraction, we can substitute 227 for π instead of 3.14. And, since 227 is also an approximation of π, we will use the ≈ symbol to show we have an approximate value.
Example 5.6.12:
A circle has radius 1415 meter. Approximate its (a) circumference and (b) area.
Solution
(a) Find the circumference when r = 1415
| Write the formula for circumference. | C = 2πr |
| Substitute 227 for π and 1415 for r . | C≈2(227)(1415) |
| Multiply. | C ≈ 8815 meters |
.(b) Find the area when r = 1415.
| Write the formula for area. | A = πr2 |
| Substitute 227 for π and 1415 for r. | A≈(227)(1415)2 |
| Multiply. | A ≈ 616225 square meters |
Exercise 5.6.23:
A circle has radius 521 meters. Approximate its (a) circumference and (b) area.
- Answer a
-
220147 m
- Answer b
- 5503087 sq. m
Exercise 5.6.24:
A circle has radius 1033 inches. Approximate its (a) circumference and (b) area.
- Answer a
-
4021 in.
- Answer b
- 200693 sq. in.
ACCESS ADDITIONAL ONLINE RESOURCES
Converting a Fraction to a Decimal - Part 2
Convert a Fraction to a Decimal (repeating)
Compare Fractions and Decimals using Inequality Symbols
Determine the Area of a Circle
Determine the Circumference of a Circle
Practice Makes Perfect
Convert Fractions to Decimals
In the following exercises, convert each fraction to a decimal.
- 25
- 45
- −38
- −58
- 1720
- 1320
- 114
- 174
- −31025
- −28425
- 59
- 29
- 1511
- 1811
- 15111
- 25111
In the following exercises, simplify the expression.
- 12 + 6.5
- 14 + 10.75
- 2.4 + 58
- 3.9 + 920
- 9.73 + 1720
- 6.29 + 2140
Order Decimals and Fractions
In the following exercises, order each pair of numbers, using < or >.
- 18___0.8
- 14___0.4
- 25___0.25
- 35___0.35
- 0.725___34
- 0.92___78
- 0.66___23
- 0.83___56
- −0.75___−45
- −0.44___−920
- −34___−0.925
- −23___−0.632
In the following exercises, write each set of numbers in order from least to greatest.
- 35,916, 0.55
- 38,720, 0.36
- 0.702, 1320,58
- 0.15, 316,15
- −0.3, −13,−720
- −0.2, −320,−16
- −34,−79, −0.7
- −89,−45, −0.9
Simplify Expressions Using the Order of Operations
In the following exercises, simplify.
- 10(25.1 − 43.8)
- 30(18.1 − 32.5)
- 62(9.75 − 4.99)
- 42(8.45 − 5.97)
- 34(12.4 − 4.2)
- 45(8.6 + 3.9)
- 512(30.58 + 17.9)
- 916(21.96 − 9.8)
- 10 ÷ 0.1 + (1.8)4 − (0.3)2
- 5 ÷ 0.5 + (3.9)6 − (0.7)2
- (37.1 + 52.7) ÷ (12.5 ÷ 62.5)
- (11.4 + 16.2) ÷ (18 ÷ 60)
- (15)2 + (1.4)(6.5)
- (12)2 + (2.1)(8.3)
- −910⋅815 + 0.25
- −38⋅1415 + 0.72
Mixed Practice
In the following exercises, simplify. Give the answer as a decimal.
- 314 − 6.5
- 525 − 8.75
- 10.86 ÷ 23
- 5.79 ÷ 34
- 78(103.48) + 112(361)
- 516(117.6) + 213(699)
- 3.6(98−2.72)
- 5.1(125−3.91)
Find the Circumference and Area of Circles
In the following exercises, approximate the (a) circumference and (b) area of each circle. If measurements are given in fractions, leave answers in fraction form.
- radius = 5 in.
- radius = 20 in.
- radius = 9 ft.
- radius = 4 ft.
- radius = 46 cm
- radius = 38 cm
- radius = 18.6 m
- radius = 57.3 m
- radius = 710 mile
- radius = 711 mile
- radius = 38 yard
- radius = 512 yard
- diameter = 56 m
- diameter = 34 m
Everyday Math
- Kelly wants to buy a pair of boots that are on sale for 23 of the original price. The original price of the boots is $84.99. What is the sale price of the shoes?
- An architect is planning to put a circular mosaic in the entry of a new building. The mosaic will be in the shape of a circle with radius of 6 feet. How many square feet of tile will be needed for the mosaic? (Round your answer up to the next whole number.)
Writing Exercises
- Is it easier for you to convert a decimal to a fraction or a fraction to a decimal? Explain.
- Describe a situation in your life in which you might need to find the area or circumference of a circle.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section
(b) What does this checklist tell you about your mastery of this section? What steps will you take to improve?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


