9.1: Use a Problem Solving Strategy (Part 1)
- Page ID
- 21753
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Approach word problems with a positive attitude
- Use a problem solving strategy for word problems
- Solve number problems
Before you get started, take this readiness quiz.
- Translate “6 less than twice x” into an algebraic expression. If you missed this problem, review Example 2.4.13.
- Solve: \(\dfrac{2}{3}\)x = 24. If you missed this problem, review Example 8.3.4.
- Solve: 3x + 8 = 14. If you missed this problem, review Example 8.4.1.
Approach Word Problems with a Positive Attitude
The world is full of word problems. How much money do I need to fill the car with gas? How much should I tip the server at a restaurant? How many socks should I pack for vacation? How big a turkey do I need to buy for Thanksgiving dinner, and what time do I need to put it in the oven? If my sister and I buy our mother a present, how much will each of us pay?
Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student in Figure \(\PageIndex{1}\)?
Figure \(\PageIndex{1}\) - Negative thoughts about word problems can be barriers to success.
When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.
Start with a fresh slate and begin to think positive thoughts like the student in Figure \(\PageIndex{2}\). Read the positive thoughts and say them out loud.
Figure \(\PageIndex{2}\) - When it comes to word problems, a positive attitude is a big step toward success.
If we take control and believe we can be successful, we will be able to master word problems.
Think of something that you can do now but couldn't do three years ago. Whether it's driving a car, snowboarding, cooking a gourmet meal, or speaking a new language, you have been able to learn and master a new skill. Word problems are no different. Even if you have struggled with word problems in the past, you have acquired many new math skills that will help you succeed now!
Use a Problem-solving Strategy for Word Problems
In earlier chapters, you translated word phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. Since then you've increased your math vocabulary as you learned about more algebraic procedures, and you've had more practice translating from words into algebra.
You have also translated word sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. You had to restate the situation in one sentence, assign a variable, and then write an equation to solve. This method works as long as the situation is familiar to you and the math is not too complicated.
Now we'll develop a strategy you can use to solve any word problem. This strategy will help you become successful with word problems. We'll demonstrate the strategy as we solve the following problem.
Pete bought a shirt on sale for $18, which is one-half the original price. What was the original price of the shirt?
Solution
Step 1. Read the problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don't understand, look them up in a dictionary or on the Internet.
- In this problem, do you understand what is being discussed? Do you understand every word?
Step 2. Identify what you are looking for. It's hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!
- In this problem, the words “what was the original price of the shirt” tell you that what you are looking for: the original price of the shirt.
Step 3. Name what you are looking for. Choose a variable to represent that quantity. You can use any letter for the variable, but it may help to choose one that helps you remember what it represents.
- Let p = the original price of the shirt.
Step 4. Translate into an equation. It may help to first restate the problem in one sentence, with all the important information. Then translate the sentence into an equation.
Step 5. Solve the equation using good algebra techniques. Even if you know the answer right away, using algebra will better prepare you to solve problems that do not have obvious answers.
| Write the equation. | \(18 = \dfrac{1}{2} p\) |
| Multiply both sides by 2. | \(\textcolor{red}{2} \cdot 18 = \textcolor{red}{2} \cdot \dfrac{1}{2} p\) |
| Simplify. | \(36 = p\) |
Step 6. Check the answer in the problem and make sure it makes sense.
- We found that p = 36, which means the original price was $36. Does $36 make sense in the problem? Yes, because 18 is one-half of 36, and the shirt was on sale at half the original price.
Step 7. Answer the question with a complete sentence.
- The problem asked “What was the original price of the shirt?” The answer to the question is: “The original price of the shirt was $36.”
If this were a homework exercise, our work might look like this:
| Let p = the original price. | 18 is one-half the original price.$$\begin{split} 18 &= \dfrac{1}{2} p \\ 2 \cdot 18 &= 2 \cdot \dfrac{1}{2} p \\ 36 &= p \end{split}$$ |
|
Check: Is $36 a reasonable price for a shirt? Yes. Is 18 one-half of 36? Yes. |
The original price of the shirt was $36. |
Joaquin bought a bookcase on sale for $120, which was two-thirds the original price. What was the original price of the bookcase?
- Answer
-
$180
Two-fifths of the people in the senior center dining room are men. If there are 16 men, what is the total number of people in the dining room?
- Answer
-
40
We list the steps we took to solve the previous example.
- Step 1. Read the word problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don't understand, look them up in a dictionary or on the internet.
- Step 2. Identify what you are looking for.
- Step 3. Name what you are looking for. Choose a variable to represent that quantity.
- Step 4. Translate into an equation. It may be helpful to first restate the problem in one sentence before translating.
- Step 5. Solve the equation using good algebra techniques.
- Step 6. Check the answer in the problem. Make sure it makes sense.
- Step 7. Answer the question with a complete sentence.
Let's use this approach with another example.
Yash brought apples and bananas to a picnic. The number of apples was three more than twice the number of bananas. Yash brought 11 apples to the picnic. How many bananas did he bring?
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | How many bananas did he bring? |
| Step 3. Name what you are looking for. Choose a variable to represent the number of bananas. | Let b = number of bananas |
| Step 4. Translate. Restate the problem in one sentence with all the important information. Translate into an equation. |
|
| Step 5. Solve the equation. | $$11 = 3b + 3$$ |
| Subtract 3 from each side. | \(11 \textcolor{red}{-3} = 2b + 3 \textcolor{red}{-3}\) |
| Simplify. | \(8 = 2b\) |
| Divide each side by 2. | \(\dfrac{8}{\textcolor{red}{2}} = \dfrac{2b}{\textcolor{red}{2}}\) |
| Simplify. | \(4 = b\) |
| Step 6. Check: First, is our answer reasonable? Yes, bringing four bananas to a picnic seems reasonable. The problem says the number of apples was three more than twice the number of bananas. If there are four bananas, does that make eleven apples? Twice 4 bananas is 8. Three more than 8 is 11. | |
| Step 7. Answer the question. | Yash brought 4 bananas to the picnic. |
Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was 3 more than the number of notebooks. He bought 5 textbooks. How many notebooks did he buy?
- Answer
-
2
Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is seven more than the number of crossword puzzles. He completed 14 Sudoku puzzles. How many crossword puzzles did he complete?
- Answer
-
7
In Solve Sales Tax, Commission, and Discount Applications, we learned how to translate and solve basic percent equations and used them to solve sales tax and commission applications. In the next example, we will apply our Problem Solving Strategy to more applications of percent.
Nga's car insurance premium increased by $60, which was 8% of the original cost. What was the original cost of the premium?
Solution
| Step 1. Read the problem. Remember, if there are words you don't understand, look them up. | |
| Step 2. Identify what you are looking for. | the original cost of the premium |
| Step 3. Name. Choose a variable to represent the original cost of premium. | Let c = the original cost |
| Step 4. Translate. Restate as one sentence. Translate into an equation. |  |
| Step 5. Solve the equation. | $$60 = 0.08c$$ |
| Divide both sides by 0.08. | $$\dfrac{60}{\textcolor{red}{0.08}} = \dfrac{0.08c}{\textcolor{red}{0.08}}$$ |
| Simplify. | $$c = 750$$ |
| Step 6. Check: Is our answer reasonable? Yes, a $750 premium on auto insurance is reasonable. Now let's check our algebra. Is 8% of 750 equal to 60? | $$\begin{split} 750 &= c \\ 0.08(750) &= 60 \\ 60 &= 60\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The original cost of Nga's premium was $750. |
Pilar's rent increased by 4%. The increase was $38. What was the original amount of Pilar's rent?
- Answer
-
$950
Steve saves 12% of his paycheck each month. If he saved $504 last month, how much was his paycheck?
- Answer
-
$4200
Solve Number Problems
Now we will translate and solve number problems. In number problems, you are given some clues about one or more numbers, and you use these clues to build an equation. Number problems don't usually arise on an everyday basis, but they provide a good introduction to practicing the Problem Solving Strategy. Remember to look for clue words such as difference, of, and and.
The difference of a number and six is 13. Find the number.
Solution
| Step 1. Read the problem. Do you understand all the words? | |
| Step 2. Identify what you are looking for. | the number |
| Step 3. Name. Choose a variable to represent the number. | Let n = the number |
| Step 4. Translate. Restate as one sentence. Translate into an equation. |  |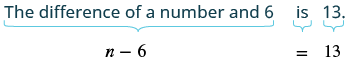
| Step 5. Solve the equation. Add 6 to both sides. Simplify. | $$\begin{split} n - 6 &= 13 \\ n - \textcolor{red}{+6} &= 13 \textcolor{red}{+6} \\ n &= 19 \end{split}$$ |
| Step 6. Check: The difference of 19 and 6 is 13. It checks. | |
| Step 7. Answer the question. | The number is 19. |
The difference of a number and eight is 17. Find the number.
- Answer
-
25
The difference of a number and eleven is −7. Find the number.
- Answer
-
4
The sum of twice a number and seven is 15. Find the number.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the number |
| Step 3. Name. Choose a variable to represent the number. | Let n = the number |
| Step 4. Translate. Restate the problem as one sentence. Translate into an equation. |  |
| Step 5. Solve the equation. | $$2n + 7 = 15$$ |
| Subtract 7 from each side and simplify. | $$2n = 8$$ |
| Divide each side by 2 and simplify. | $$n = 4$$ |
| Step 6. Check: is the sum of twice 4 and 7 equal to 15? | $$\begin{split} 2 \cdot 4 + 7 &= 15 \\ 8 + 7 &= 15 \\ 15 &= 15\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The number is 4. |
The sum of four times a number and two is 14. Find the number.
- Answer
-
3
The sum of three times a number and seven is 25. Find the number.
- Answer
-
6
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."