9.10: Solve Geometry Applications: Volume and Surface Area (Part 2)

Last updated
Save as PDF

Page ID: 21762

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Find the Volume and Surface Area of Spheres

A sphere is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below.

Showing where these formulas come from, like we did for a rectangular solid, is beyond the scope of this course. We will approximate $\pi$ with 3.14.

Definition: Volume and Surface Area of a Sphere

For a sphere with radius r:

$An image of a sphere is shown. The radius is labeled r. Beside this is Volume: V equals four-thirds times pi times r cubed. Below that is Surface Area: S equals 4 times pi times r squared.$

Example $\PageIndex{5}$:

A sphere has a radius 6 inches. Find its (a) volume and (b) surface area.

Solution

Step 1 is the same for both (a) and (b), so we will show it just once.

Step 1. Read the problem. Draw the figure and label it with the given information.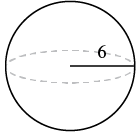

$CNX_BMath_Figure_09_06_042_img-01.png$

(a)

Step 2. Identify what you are looking for.	the volume of the sphere
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula.	$$V = \dfrac{4}{3} \pi r^{3} \tag{9.6.12}$$
Step 5. Solve.	$$\begin{split} V &\approx \dfrac{4}{3} (3.14) 6^{3} \\ V &\approx 904.32\; cubic\; inches \end{split}$$
Step 6. Check.	Double-check your math on a calculator.
Step 7. Answer the question.	The volume is approximately 904.32 cubic inches.

(b)

Step 2. Identify what you are looking for.	the surface area of the cube
Step 3. Name. Choose a variable to represent it.	let S = surface area
Step 4. Translate. Write the appropriate formula.	$$S = 4 \pi r^{2} \tag{9.6.13}$$
Step 5. Solve.	$$\begin{split} S &\approx 4 (3.14) 6^{2} \\ S &\approx 452.16\; sq.\; inches \end{split}$$
Step 6. Check.	Double-check your math on a calculator.
Step 7. Answer the question.	The surface area is approximately 452.16 square inches.

Exercise $\PageIndex{9}$:

Find the (a) volume and (b) surface area of a sphere with radius 3 centimeters.

Answer a: 113.04 cu. cm

Answer b: 113.04 sq. cm

Exercise $\PageIndex{10}$:

Find the (a) volume and (b) surface area of each sphere with a radius of 1 foot

Answer a: 4.19 cu. ft

Answer b: 12.56 sq. ft

Example $\PageIndex{6}$:

A globe of Earth is in the shape of a sphere with radius 14 centimeters. Find its (a) volume and (b) surface area. Round the answer to the nearest hundredth.

Step 1. Read the problem. Draw the figure and label it with the given information.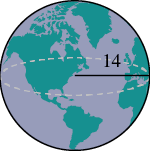

$CNX_BMath_Figure_09_06_043_img-01.png$

(a)

Step 2. Identify what you are looking for.	the volume of the sphere
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula. Substitute. (Use 3.14 for $\pi$)	$$\begin{split} V &= \dfrac{4}{3} \pi r^{3} \\ V &\approx \dfrac{4}{3} (3.14) 14^{3} \end{split}$$
Step 5. Solve.	$$V \approx 11,488.21 \tag{9.6.14}$$
Step 6. Check.	We leave it to you to check your calculations.
Step 7. Answer the question.	The volume is approximately 11,488.21 cubic inches.

(b)

Step 2. Identify what you are looking for.	the surface area of the sphere
Step 3. Name. Choose a variable to represent it.	let S = surface area
Step 4. Translate. Write the appropriate formula.	$$\begin{split} S &= 4 \pi r^{2} \\ S &\approx 4(3.14) 14^{2} \end{split}$$
Step 5. Solve.	$$S \approx 2461.76 \tag{9.6.15}$$
Step 6. Check.	We leave it to you to check your calculations.
Step 7. Answer the question.	The surface area is approximately 2461.76 square inches.

Exercise $\PageIndex{11}$:

A beach ball is in the shape of a sphere with radius of 9 inches. Find its (a) volume and (b) surface area.

Answer a: 3052.08 cu. in

Answer b: 1017.36 sq. in.

Exercise $\PageIndex{12}$:

A Roman statue depicts Atlas holding a globe with radius of 1.5 feet. Find the (a) volume and (b) surface area of the globe.

Answer a: 14.13 cu. ft

Answer b: 28.26 sq. ft

Find the Volume and Surface Area of a Cylinder

If you have ever seen a can of soda, you know what a cylinder looks like. A cylinder is a solid figure with two parallel circles of the same size at the top and bottom. The top and bottom of a cylinder are called the bases. The height h of a cylinder is the distance between the two bases. For all the cylinders we will work with here, the sides and the height, h, will be perpendicular to the bases.

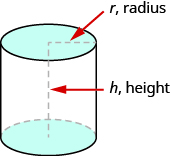
$An image of a cylinder is shown. There is a red arrow pointing to the radius of the top labeling it r, radius. There is a red arrow pointing to the height of the cylinder labeling it h, height.$

Figure $\PageIndex{5}$ - A cylinder has two circular bases of equal size. The height is the distance between the bases.

Rectangular solids and cylinders are somewhat similar because they both have two bases and a height. The formula for the volume of a rectangular solid, V = Bh, can also be used to find the volume of a cylinder.

For the rectangular solid, the area of the base, B, is the area of the rectangular base, length × width. For a cylinder, the area of the base, B, is the area of its circular base, $\pi$r². Figure $\PageIndex{6}$ compares how the formula V = Bh is used for rectangular solids and cylinders.

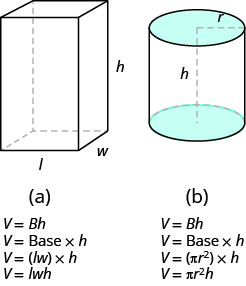
$In (a), a rectangular solid is shown. The sides are labeled L, W, and H. Below this is V equals capital Bh, then V equals Base times h, then V equals parentheses lw times h, then V equals lwh. In (b), a cylinder is shown. The radius of the top is labeled r, the height is labeled h. Below this is V equals capital Bh, then V equals Base times h, then V equals parentheses pi r squared times h, then V equals pi times r squared times h.$

Figure $\PageIndex{6}$ - Seeing how a cylinder is similar to a rectangular solid may make it easier to understand the formula for the volume of a cylinder.

To understand the formula for the surface area of a cylinder, think of a can of vegetables. It has three surfaces: the top, the bottom, and the piece that forms the sides of the can. If you carefully cut the label off the side of the can and unroll it, you will see that it is a rectangle. See Figure $\PageIndex{7}$.

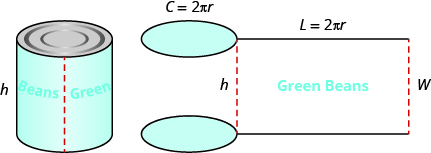
$A cylindrical can of green beans is shown. The height is labeled h. Beside this are pictures of circles for the top and bottom of the can and a rectangle for the other portion of the can. Above the circles is C equals 2 times pi times r. The top of the rectangle says l equals 2 times pi times r. The left side of the rectangle is labeled h, the right side is labeled w.$

Figure $\PageIndex{7}$ - By cutting and unrolling the label of a can of vegetables, we can see that the surface of a cylinder is a rectangle. The length of the rectangle is the circumference of the cylinder’s base, and the width is the height of the cylinder.

The distance around the edge of the can is the circumference of the cylinder’s base it is also the length L of the rectangular label. The height of the cylinder is the width W of the rectangular label. So the area of the label can be represented as

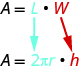
$The top line says A equals l times red w. Below the l is 2 times pi times r. Below the w is a red h.$

To find the total surface area of the cylinder, we add the areas of the two circles to the area of the rectangle.

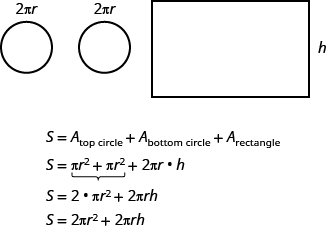
$A rectangle is shown with circles coming off the top and bottom.$

The surface area of a cylinder with radius r and height h, is

\[S = 2 \pi r^{2} + 2 \pi rh \tag{9.6.16}\]

Definition: Volume and Surface Area of a Cylinder

For a cylinder with radius r and height h:

$A cylinder is shown. The height is labeled h and the radius of the top is labeled r. Beside it is Volume: V equals pi times r squared times h or V equals capital B times h. Below this is Surface Area: S equals 2 times pi times r squared plus 2 times pi times r times h.$

Example $\PageIndex{7}$:

A cylinder has height 5 centimeters and radius 3 centimeters. Find the (a) volume and (b) surface area.

Solution

Step 1. Read the problem. Draw the figure and label it with the given information.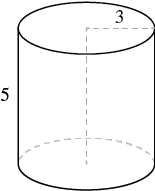

$CNX_BMath_Figure_09_06_046_img-01.png$

(a)

Step 2. Identify what you are looking for.	the volume of the cylinder
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula. Substitute. (Use 3.14 for $\pi$)	$$\begin{split} V &= \pi r^{2} h \\ V &\approx (3.14) 3^{2} \cdot 5 \end{split}$$
Step 5. Solve.	$$V \approx 141.3 \tag{9.6.17}$$
Step 6. Check.	We leave it to you to check your calculations.
Step 7. Answer the question.	The volume is approximately 141.3 cubic inches.

(b)

Step 2. Identify what you are looking for.	the surface area of the cylinder
Step 3. Name. Choose a variable to represent it.	let S = surface area
Step 4. Translate. Write the appropriate formula.	$$\begin{split} S &= 2 \pi r^{2} + 2 \pi rh \\ S &\approx 2(3.14)3^{2} + 2(3.14)(3)5 \end{split}$$
Step 5. Solve.	$$S \approx 150.72 \tag{9.6.18}$$
Step 6. Check.	We leave it to you to check your calculations.
Step 7. Answer the question.	The surface area is approximately 150.72 square inches.

Exercise $\PageIndex{13}$:

Find the (a) volume and (b) surface area of the cylinder with radius 4 cm and height 7 cm.

Answer a: 351.68 cu. cm

Answer b: 276.32 sq. ft

Exercise $\PageIndex{14}$:

Find the (a) volume and (b) surface area of the cylinder with given radius 2 ft and height 8 ft.

Answer a: 100.48 cu. ft

Answer b: 125.6 sq. ft

Example $\PageIndex{8}$:

Find the (a) volume and (b) surface area of a can of soda. The radius of the base is 4 centimeters and the height is 13 centimeters. Assume the can is shaped exactly like a cylinder.

Solution

Step 1. Read the problem. Draw the figure and label it with the given information.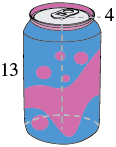

$CNX_BMath_Figure_09_06_047_img-01.png$

(a)

Step 2. Identify what you are looking for.	the volume of the cylinder
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula. Substitute. (Use 3.14 for $\pi$)	$$\begin{split} V &= \pi r^{2} h \\ V &\approx (3.14) 4^{2} \cdot 13 \end{split}$$
Step 5. Solve.	$$V \approx 653.12 \tag{9.6.19}$$
Step 6. Check.	We leave it to you to check.
Step 7. Answer the question.	The volume is approximately 653.12 cubic centimeters.

(b)

Step 2. Identify what you are looking for.	the surface area of the cylinder
Step 3. Name. Choose a variable to represent it.	let S = surface area
Step 4. Translate. Write the appropriate formula.	$$\begin{split} S &= 2 \pi r^{2} + 2 \pi rh \\ S &\approx 2(3.14)4^{2} + 2(3.14)(4)13 \end{split}$$
Step 5. Solve.	$$S \approx 427.04 \tag{9.6.20}$$
Step 6. Check.	We leave it to you to check your calculations.
Step 7. Answer the question.	The surface area is approximately 427.04 square centimeters.

Exercise $\PageIndex{15}$:

Find the (a) volume and (b) surface area of a can of paint with radius 8 centimeters and height 19 centimeters. Assume the can is shaped exactly like a cylinder.

Answer a: 3,818.24 cu. cm

Answer b: 1,356.48 sq. cm

Exercise $\PageIndex{16}$:

Find the (a) volume and (b) surface area of a cylindrical drum with radius 2.7 feet and height 4 feet. Assume the drum is shaped exactly like a cylinder.

Answer a: 91.5624 cu. ft

Answer b: 113.6052 sq. ft

Find the Volume of Cones

The first image that many of us have when we hear the word ‘cone’ is an ice cream cone. There are many other applications of cones (but most are not as tasty as ice cream cones). In this section, we will see how to find the volume of a cone.

In geometry, a cone is a solid figure with one circular base and a vertex. The height of a cone is the distance between its base and the vertex.The cones that we will look at in this section will always have the height perpendicular to the base. See Figure $\PageIndex{8}$.

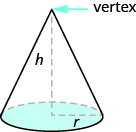
$An image of a cone is shown. The top is labeled vertex. The height is labeled h. The radius of the base is labeled r.$

Figure $\PageIndex{8}$ - The height of a cone is the distance between its base and the vertex.

Earlier in this section, we saw that the volume of a cylinder is V = $\pi$r²h. We can think of a cone as part of a cylinder. Figure $\PageIndex{9}$ shows a cone placed inside a cylinder with the same height and same base. If we compare the volume of the cone and the cylinder, we can see that the volume of the cone is less than that of the cylinder.

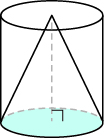
$An image of a cone is shown. There is a cylinder drawn around it.$

Figure $\PageIndex{9}$ - The volume of a cone is less than the volume of a cylinder with the same base and height.

In fact, the volume of a cone is exactly one-third of the volume of a cylinder with the same base and height. The volume of a cone is

\[V = \dfrac{1}{3} \textcolor{blue}{B} h \tag{9.6.21}\]

Since the base of a cone is a circle, we can substitute the formula of area of a circle, $\pi$r², for B to get the formula for volume of a cone.

\[V = \dfrac{1}{3} \textcolor{blue}{\pi r^{2}} h \tag{9.6.22}\]

In this book, we will only find the volume of a cone, and not its surface area.

Definition: Volume of a Cone

For a cone with radius r and height h .

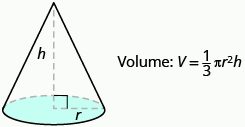
$An image of a cone is shown. The height is labeled h, the radius of the base is labeled r. Beside this is Volume: V equals one-third times pi times r squared times h.$

Example $\PageIndex{9}$:

Find the volume of a cone with height 6 inches and radius of its base 2 inches.

Solution

Step 1. Read the problem. Draw the figure and label it with the given information.	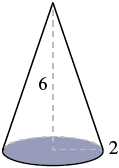$CNX_BMath_Figure_09_06_048_img-01.png$
Step 2. Identify what you are looking for.	the volume of the cone
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula. Substitute. (Use 3.14 for $\pi$)	$$\begin{split} V &= \dfrac{1}{3} \pi r^{2} h \\ V &\approx \dfrac{1}{3} (3.14)(2)^{2} (6) \end{split}$$
Step 5. Solve.	$$V \approx 25.12 \tag{9.6.23}$$
Step 6. Check.	We leave it to you to check your calculations.
Step 7. Answer the question.	The volume is approximately 25.12 cubic inches.

Exercise $\PageIndex{17}$:

Find the volume of a cone with height 7 inches and radius 3 inches

Answer: 65.94 cu. in.

Exercise $\PageIndex{18}$:

Find the volume of a cone with height 9 centimeters and radius 5 centimeters

Answer: 235.5 cu. cm

Example $\PageIndex{10}$:

Marty’s favorite gastro pub serves French fries in a paper wrap shaped like a cone. What is the volume of a conic wrap that is 8 inches tall and 5 inches in diameter? Round the answer to the nearest hundredth.

Solution

Step 1. Read the problem. Draw the figure and label it with the given information.	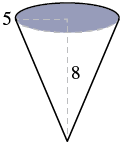$CNX_BMath_Figure_09_06_049_img-01.png$
Step 2. Identify what you are looking for.	the volume of the cone
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula. Substitute. (Use 3.14 for $\pi$, and notice that we were given the distance across the circle, which is its diameter. The radius is 2.5 inches.)	$$\begin{split} V &= \dfrac{1}{3} \pi r^{2} h \\ V &\approx \dfrac{1}{3} (3.14)(2.5)^{2} (8) \end{split}$$
Step 5. Solve.	$$V \approx 52.33 \tag{9.6.24}$$
Step 6. Check.	We leave it to you to check your calculations.
Step 7. Answer the question.	The volume of the wrap is approximately 52.33 cubic inches.

Exercise $\PageIndex{19}$:

How many cubic inches of candy will fit in a cone-shaped piñata that is 18 inches long and 12 inches across its base? Round the answer to the nearest hundredth.

Answer: 678.24 cu. in.

Exercise $\PageIndex{20}$:

What is the volume of a cone-shaped party hat that is 10 inches tall and 7 inches across at the base? Round the answer to the nearest hundredth.

Answer: 128.2 cu. in.

Summary of Geometry Formulas

The following charts summarize all of the formulas covered in this chapter.

$A table is shown that summarizes all of the formulas in the chapter. The first cell is for Supplementary and Complementary Angles, and says that the measure of angle A plus the measure of angle B equals 180 degrees for supplementary angles A and B and the measure of angle C plus the measure of angle D equals 90 degrees for complementary angles C and D. There is an image of two angles A and B that together form a straight line and two angles C and D that together form a right angle. The next cell says Rectangular Solid and shows the formulas Volume equals LWH and Surface Area equals 2LH plus 2LW plus 2WH. An image of a rectangular solid with sides L, W, and H is shown. The next cell says Triangle. An image of a triangle is shown with sides a, b, and c, vertices A, B, and C, and height h. It says, “For triangle ABC, angle measures measure of angle A plus measure of angle B plus measure of angle C equal 180 degrees. Below this is Perimeter, P equals a plus b plus c. Below this is Area, A equals one-half bh. The next cell says Cube and shows an image of a cube with sides s. It says Volume V equals s cubed and Surface Area S equals 6 times s squared. The next cell says Similar Triangles. It shows two similar triangles ABC and XYZ. It says if triangle ABC is similar to triangle XYZ, then measure of angle A equals measure of angle X, measure of angle B equals measure of angle Y, and measure of angle C equals measure of angle Z. It then says a over x equals b over y equal c over z. The next cell says Sphere and shows an image of a sphere with radius r. It says volume V equals four-thirds times pi times r and Surface Area S equals 4 times pi times r squared. The next cell says Circle. There is an image with two radii labeled r and the diameter labeled d. It says Circumference C equals 2 pi times r and C equals pi times d. It says Area equals pi times r squared. The next cell says Cylinder and shows an image of a cylinder with height h and radius of the base r. It says Volume V equals pi times r squared times h. Below this is V equals Bh. Below that is Surface Area S equals 2 times pi times r squared plus 2 times pi times rh. The next cell says Rectangle and shows an image of a rectangle with sides W and L. It says Perimeter P equals 2L plus 2W, then Area A equals LW. The next cell says Cone and shows an image of a cone with height h and radius of the base r. It says Volume V equals one-third times pi times r squared times h. The last cell says Trapezoid and shows an image of a trapezoid with bases little b and capital B, and height h. It says Area A equals one-half times h times parentheses little b plus capital B.$

ACCESS ADDITIONAL ONLINE RESOURCES

Volume of a Cone

Practice Makes Perfect

Find Volume and Surface Area of Rectangular Solids

In the following exercises, find (a) the volume and (b) the surface area of the rectangular solid with the given dimensions.

length 2 meters, width 1.5 meters, height 3 meters
length 5 feet, width 8 feet, height 2.5 feet
length 3.5 yards, width 2.1 yards, height 2.4 yards
length 8.8 centimeters, width 6.5 centimeters, height 4.2 centimeters

In the following exercises, solve.

Moving van A rectangular moving van has length 16 feet, width 8 feet, and height 8 feet. Find its (a) volume and (b) surface area.
Gift box A rectangular gift box has length 26 inches, width 16 inches, and height 4 inches. Find its (a) volume and (b) surface area.
Carton A rectangular carton has length 21.3 cm, width 24.2 cm, and height 6.5 cm. Find its (a) volume and (b) surface area.
Shipping container A rectangular shipping container has length 22.8 feet, width 8.5 feet, and height 8.2 feet. Find its (a) volume and (b) surface area.

In the following exercises, find (a) the volume and (b) the surface area of the cube with the given side length.

5 centimeters
6 inches
10.4 feet
12.5 meters

In the following exercises, solve.

Science center Each side of the cube at the Discovery Science Center in Santa Ana is 64 feet long. Find its (a) volume and (b) surface area.
Museum A cube-shaped museum has sides 45 meters long. Find its (a) volume and (b) surface area.
Base of statue The base of a statue is a cube with sides 2.8 meters long. Find its (a) volume and (b) surface area.
Tissue box A box of tissues is a cube with sides 4.5 inches long. Find its (a) volume and (b) surface area.

Find the Volume and Surface Area of Spheres

In the following exercises, find (a) the volume and (b) the surface area of the sphere with the given radius. Round answers to the nearest hundredth.

3 centimeters
9 inches
7.5 feet
2.1 yards

In the following exercises, solve. Round answers to the nearest hundredth.

Exercise ball An exercise ball has a radius of 15 inches. Find its (a) volume and (b) surface area.
Balloon ride The Great Park Balloon is a big orange sphere with a radius of 36 feet . Find its (a) volume and (b) surface area.
Golf ball A golf ball has a radius of 4.5 centimeters. Find its (a) volume and (b) surface area.
Baseball A baseball has a radius of 2.9 inches. Find its (a) volume and (b) surface area.

Find the Volume and Surface Area of a Cylinder

In the following exercises, find (a) the volume and (b) the surface area of the cylinder with the given radius and height. Round answers to the nearest hundredth.

radius 3 feet, height 9 feet
radius 5 centimeters, height 15 centimeters
radius 1.5 meters, height 4.2 meters
radius 1.3 yards, height 2.8 yards

In the following exercises, solve. Round answers to the nearest hundredth.

Coffee can A can of coffee has a radius of 5 cm and a height of 13 cm. Find its (a) volume and (b) surface area.
Snack pack A snack pack of cookies is shaped like a cylinder with radius 4 cm and height 3 cm. Find its (a) volume and (b) surface area.
Barber shop pole A cylindrical barber shop pole has a diameter of 6 inches and height of 24 inches. Find its (a) volume and (b) surface area.
Architecture A cylindrical column has a diameter of 8 feet and a height of 28 feet. Find its (a) volume and (b) surface area.

Find the Volume of Cones

In the following exercises, find the volume of the cone with the given dimensions. Round answers to the nearest hundredth.

height 9 feet and radius 2 feet
height 8 inches and radius 6 inches
height 12.4 centimeters and radius 5 cm
height 15.2 meters and radius 4 meters

In the following exercises, solve. Round answers to the nearest hundredth.

Teepee What is the volume of a cone-shaped teepee tent that is 10 feet tall and 10 feet across at the base?
Popcorn cup What is the volume of a cone-shaped popcorn cup that is 8 inches tall and 6 inches across at the base?
Silo What is the volume of a cone-shaped silo that is 50 feet tall and 70 feet across at the base?
Sand pile What is the volume of a cone-shaped pile of sand that is 12 meters tall and 30 meters across at the base?

Everyday Math

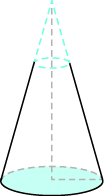
Street light post The post of a street light is shaped like a truncated cone, as shown in the picture below. It is a large cone minus a smaller top cone. The large cone is 30 feet tall with base radius 1 foot. The smaller cone is 10 feet tall with base radius of 0.5 feet. To the nearest tenth, (a) find the volume of the large cone. (b) find the volume of the small cone. (c) find the volume of the post by subtracting the volume of the small cone from the volume of the large cone.

$An image of a cone is shown. There is a dark dotted line at the top indicating a smaller cone.$

Ice cream cones A regular ice cream cone is 4 inches tall and has a diameter of 2.5 inches. A waffle cone is 7 inches tall and has a diameter of 3.25 inches. To the nearest hundredth, (a) find the volume of the regular ice cream cone. (b) find the volume of the waffle cone. (c) how much more ice cream fits in the waffle cone compared to the regular cone?

Writing Exercises

The formulas for the volume of a cylinder and a cone are similar. Explain how you can remember which formula goes with which shape.
Which has a larger volume, a cube of sides of 8 feet or a sphere with a diameter of 8 feet? Explain your reasoning.

Self Check

(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$CNX_BMath_Figure_AppB_056.jpg$

(b) After reviewing this checklist, what will you do to become confident for all objectives?

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."

Search

Text Color

Text Size

Margin Size

Font Type

Find the Volume and Surface Area of Spheres

Definition: Volume and Surface Area of a Sphere

Example \(\PageIndex{5}\):

Exercise \(\PageIndex{9}\):

Exercise \(\PageIndex{10}\):

Example \(\PageIndex{6}\):

Exercise \(\PageIndex{11}\):

Exercise \(\PageIndex{12}\):

Find the Volume and Surface Area of a Cylinder

Definition: Volume and Surface Area of a Cylinder

Example \(\PageIndex{7}\):

Exercise \(\PageIndex{13}\):

Exercise \(\PageIndex{14}\):

Example \(\PageIndex{8}\):

Exercise \(\PageIndex{15}\):

Exercise \(\PageIndex{16}\):

Find the Volume of Cones

Definition: Volume of a Cone

Example \(\PageIndex{9}\):

Exercise \(\PageIndex{17}\):

Exercise \(\PageIndex{18}\):

Example \(\PageIndex{10}\):

Exercise \(\PageIndex{19}\):

Exercise \(\PageIndex{20}\):

Summary of Geometry Formulas

ACCESS ADDITIONAL ONLINE RESOURCES

Practice Makes Perfect

Find Volume and Surface Area of Rectangular Solids

Find the Volume and Surface Area of Spheres

Find the Volume and Surface Area of a Cylinder

Find the Volume of Cones

Everyday Math

Writing Exercises

Self Check

Contributors and Attributions