9.11: Solve a Formula for a Specific Variable

Last updated
Save as PDF

Page ID: 21763

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Learning Objectives

Use the distance, rate, and time formula
Solve a formula for a specific variable

Be Prepared!

Before you get started, take this readiness quiz.

Write 35 miles per gallon as a unit rate. If you missed this problem, review Example 5.11.8.
Solve 6x + 24 = 96. If you missed this problem, review Example 8.4.1.
Find the simple interest earned after 5 years on $1,000 at an interest rate of 4%. If you missed this problem, review Example 6.4.1.

Use the Distance, Rate, and Time Formula

One formula you’ll use often in algebra and in everyday life is the formula for distance traveled by an object moving at a constant speed. The basic idea is probably already familiar to you. Do you know what distance you travel if you drove at a steady rate of 60 miles per hour for 2 hours? (This might happen if you use your car’s cruise control while driving on the Interstate.) If you said 120 miles, you already know how to use this formula!

The math to calculate the distance might look like this:

\[\begin{split} distance &= \left(\dfrac{60\; miles}{1\; hour}\right) (2\; hours) \\ distance &= 120\; miles \end{split}\]

In general, the formula relating distance, rate, and time is

\[distance = rate \cdot time\]

Definition: Distance, Rate and Time

For an object moving in at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula

\[d = rt\]

where d = distance, r = rate, and t = time.

Notice that the units we used above for the rate were miles per hour, which we can write as a ratio $\dfrac{miles}{hour}$. Then when we multiplied by the time, in hours, the common units ‘hour’ divided out. The answer was in miles.

Example $\PageIndex{1}$:

Jamal rides his bike at a uniform rate of 12 miles per hour for $3 \dfrac{1}{2}$ hours. How much distance has he traveled?

Solution

Step 1. Read the problem. You may want to create a mini-chart to summarize the information in the problem.	$$\begin{split} d &=\; ? \\ r &= 12\; mph \\ t &= 3 \dfrac{1}{2}\; hours \end{split}$$
Step 2. Identify what you are looking for.	distance traveled
Step 3. Name. Choose a variable to represent it.	let d = distance
Step 4. Translate. Write the appropriate formula for the situation. Substitute in the given information.	$$\begin{split} d &= rt \\ d &= 12 \cdot 3 \dfrac{1}{2} \end{split}$$
Step 5. Solve the equation.	d = 42 miles
Step 6. Check: Does 42 miles make sense?	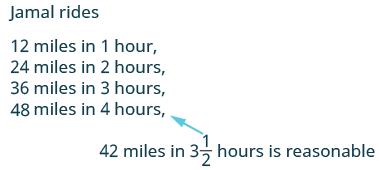$CNX_BMath_Figure_09_07_009_img-01.png$
Step 7. Answer the question with a complete sentence.	Jamal rode 42 miles.

Exercise $\PageIndex{1}$:

Lindsay drove for $5 \dfrac{1}{2}$ hours at 60 miles per hour. How much distance did she travel?

Answer: 330 mi

Exercise $\PageIndex{2}$:

Trinh walked for $2 \dfrac{1}{3}$ hours at 3 miles per hour. How far did she walk?

Answer: 7 mi

Example $\PageIndex{2}$:

Rey is planning to drive from his house in San Diego to visit his grandmother in Sacramento, a distance of 520 miles. If he can drive at a steady rate of 65 miles per hour, how many hours will the trip take?

Solution

Step 1. Read the problem. Summarize the information in the problem.	$$\begin{split} d &= 520\; miles \\ r &= 65\; mph \\ t &=\; ? \end{split}$$
Step 2. Identify what you are looking for.	how many hours (time)
Step 3. Name. Choose a variable to represent it.	let t = time
Step 4. Translate. Write the appropriate formula for the situation. Substitute in the given information.	$$\begin{split} d &= rt \\ 520 &= 65t \end{split}$$
Step 5. Solve the equation.	t = 8
Step 6. Check: Substitute the numbers into the formula and make sure the result is a true statement.	$$\begin{split} d &= rt \\ 520 &\stackrel{?}{=} 65 \cdot 8 \\ 520 &= 520\; \checkmark \end{split}$$
Step 7. Answer the question with a complete sentence. We know the units of time will be hours because we divided miles by miles per hour.	Rey's trip will take 8 hours.

Exercise $\PageIndex{3}$:

Lee wants to drive from Phoenix to his brother’s apartment in San Francisco, a distance of 770 miles. If he drives at a steady rate of 70 miles per hour, how many hours will the trip take?

Answer: 11 hours

Exercise $\PageIndex{4}$:

Yesenia is 168 miles from Chicago. If she needs to be in Chicago in 3 hours, at what rate does she need to drive?

Answer: 56 mph

Solve a Formula for a Specific Variable

In this chapter, you became familiar with some formulas used in geometry. Formulas are also very useful in the sciences and social sciences—fields such as chemistry, physics, biology, psychology, sociology, and criminal justice. Healthcare workers use formulas, too, even for something as routine as dispensing medicine. The widely used spreadsheet program Microsoft Excel^TM relies on formulas to do its calculations. Many teachers use spreadsheets to apply formulas to compute student grades. It is important to be familiar with formulas and be able to manipulate them easily.

In Example 9.57 and Example 9.58, we used the formula d = rt. This formula gives the value of d when you substitute in the values of r and t. But in Example 9.58, we had to find the value of t. We substituted in values of d and r and then used algebra to solve to t. If you had to do this often, you might wonder why there isn’t a formula that gives the value of t when you substitute in the values of d and r. We can get a formula like this by solving the formula d = rt for t.

To solve a formula for a specific variable means to get that variable by itself with a coefficient of 1 on one side of the equation and all the other variables and constants on the other side. We will call this solving an equation for a specific variable in general. This process is also called solving a literal equation. The result is another formula, made up only of variables. The formula contains letters, or literals.

Let’s try a few examples, starting with the distance, rate, and time formula we used above.

Example $\PageIndex{3}$:

Solve the formula d = rt for t: (a) when d = 520 and r = 65 (b) in general.

Solution

We’ll write the solutions side-by-side so you can see that solving a formula in general uses the same steps as when we have numbers to substitute.

	(a) when d = 520 and r = 65	(b) in general
Write the formula.	d = rt	d = rt
Substitute any given values.	520 = 65t
Divide to isolate t.	$$\dfrac{520}{65} = \dfrac{65t}{65}$$	$$\dfrac{d}{r} = \dfrac{rt}{r}$$
Simplify.	$$\begin{split} 8 &= t \\ t &= 8 \end{split}$$	$$\begin{split} \dfrac{d}{r} &= t \\ t &= \dfrac{d}{r} \end{split}$$

Notice that the solution for (a) is the same as that in Example 9.58. We say the formula t = $\dfrac{d}{r}$ is solved for t. We can use this version of the formula anytime we are given the distance and rate and need to find the time.

Exercise $\PageIndex{5}$:

Solve the formula d = rt for r: (a) when d = 180 and t = 4 (b) in general

Answer a: $r = 45$

Answer b: $r = \frac{d}{t}$

Exercise $\PageIndex{6}$:

Solve the formula d = rt for r: (a) when d = 780 and t = 12 (b) in general

Answer a: $r = 65$

Answer b: $r = \frac{d}{t}$

We used the formula A = $\dfrac{1}{2}$bh in Use Properties of Rectangles, Triangles, and Trapezoids to find the area of a triangle when we were given the base and height. In the next example, we will solve this formula for the height.

Example $\PageIndex{4}$:

The formula for area of a triangle is A = $\dfrac{1}{2}$bh. Solve this formula for h: (a) when A = 90 and b = 15 (b) in general

Solution

	(a) when A = 90 and b = 15	(b) in general
Write the formula.	A = $\dfrac{1}{2}$bh	A = $\dfrac{1}{2}$bh
Substitute any given values.	$$90 = \dfrac{1}{2} \cdot 15 \cdot h$$
Clear the fractions.	$$\textcolor{red}{2} \cdot 90 = \textcolor{red}{2} \cdot \dfrac{1}{2} \cdot 15 \cdot h$$	$$\textcolor{red}{2} \cdot A = \textcolor{red}{2} \cdot \dfrac{1}{2} \cdot b \cdot h$$
Simplify.	180 = 15h	2A = bh
Solve for h.	12 = h	$\dfrac{2A}{b}$ = h

We can now find the height of a triangle, if we know the area and the base, by using the formula

\[h = \dfrac{2A}{b}\]

Exercise $\PageIndex{7}$:

Use the formula A = $\dfrac{1}{2}$bh to solve for h: (a) when A = 170 and b = 17 (b) in general

Answer a: $h = 20$

Answer b: $h = \frac{2A}{b}$

Exercise $\PageIndex{8}$:

Use the formula A = $\dfrac{1}{2}$bh to solve for b: (a) when A = 62 and h = 31 (b) in general

Answer a: $b = 4$

Answer b: $b = \frac{2A}{h}$

In Solve Simple Interest Applications, we used the formula I = Prt to calculate simple interest, where I is interest, P is principal, r is rate as a decimal, and t is time in years.

Example $\PageIndex{5}$:

Solve the formula I = Prt to find the principal, P: (a) when I = $5,600, r = 4%, t = 7 years (b) in general

Solution

	(a) when I = $5,600, r = 4%, t = 7 years	(b) in general
Write the forumla.	I = Prt	I = Prt
Substitute any given values.	5600 = P(0.04)(7)	I = Prt
Multiply r • t.	5600 = P(0.28)	I = P(rt)
Divide to isolate P.	$$\dfrac{5600}{\textcolor{red}{0.28}} = \dfrac{P(0.28)}{\textcolor{red}{0.28}}$$	$$\dfrac{I}{\textcolor{red}{rt}} = \dfrac{P(rt)}{\textcolor{red}{rt}}$$
Simplify.	20,000 = P	$\dfrac{I}{rt}$ = P
State the answer.	The principal is $20,000.	$$P = \dfrac{I}{rt}$$

Exercise $\PageIndex{9}$:

Use the formula I = Prt. Find t: (a) when I = $2,160, r = 6%, P = $12,000; (b) in general

Answer a: $t = 3$ years

Answer b: $t = \frac{I}{Pr}$

Exercise $\PageIndex{10}$:

Use the formula I = Prt. Find r: (a) when I = $5,400, P = $9,000, t = 5 years; (b) in general

Answer a: $r = 0.12 = 12\%$

Answer b: $t = \frac{I}{Pt}$

Later in this course, and in future algebra classes, you’ll encounter equations that relate two variables, usually x and y. You might be given an equation that is solved for y and need to solve it for x, or vice versa. In the following example, we’re given an equation with both x and y on the same side and we’ll solve it for y. To do this, we will follow the same steps that we used to solve a formula for a specific variable.

Example $\PageIndex{6}$:

Solve the formula 3x + 2y = 18 for y: (a) when x = 4 (b) in general

Solution

	(a) when x = 4	(b) in general
Write the equation.	3x + 2y = 18	3x + 2y = 18
Substitute any given values.	3(4) + 2y = 18	3x + 2y = 18
Simplify if possible.	12 + 2y = 18	3x + 2y = 18
Subtract to isolate the y-term.	$$12 \textcolor{red}{-12} + 2y = 18 \textcolor{red}{-12}$$	$$3x \textcolor{red}{-3x}+ 2y = 18 \textcolor{red}{-3x}$$
Simplify.	2y = 6	2y = 18 - 3x
Divide.	$$\dfrac{2y}{\textcolor{red}{2}} = \dfrac{6}{\textcolor{red}{2}}$$	$$\dfrac{2y}{\textcolor{red}{2}} = \dfrac{18 - 3x}{\textcolor{red}{2}}$$
Simplify.	y = 3	$$y = \dfrac{18 - 3x}{2}$$

Exercise $\PageIndex{11}$:

Solve the formula 3x + 4y = 10 for y: (a) when x = 2 (b) in general

Answer a: $y = 1$

Answer b: $y = \frac{10-3x}{4}$

Exercise $\PageIndex{12}$:

Solve the formula 5x + 2y = 18 for y: (a) when x = 4 (b) in general

Answer a: $y = -1$

Answer b: $y = \frac{18-5x}{2}$

In the previous examples, we used the numbers in part (a) as a guide to solving in general in part (b). Do you think you’re ready to solve a formula in general without using numbers as a guide?

Example $\PageIndex{7}$:

Solve the formula P = a + b + c for a.

Solution

We will isolate a on one side of the equation.

We will isolate a on one side of the equation.
Write the equation.	P = a + b + c
Subtract b and c from both sides to isolate a.	$$P \textcolor{red}{-b -c} = a + b + c \textcolor{red}{-b -c}$$
Simplify.	P − b − c = a

So, a = P − b − c.

Exercise $\PageIndex{13}$:

Solve the formula P = a + b + c for b.

Answer: b = P - a - c

Exercise $\PageIndex{14}$:

Solve the formula P = a + b + c for c.

Answer: c = P - a - b

Example $\PageIndex{8}$:

Solve the equation 3x + y = 10 for y.

Solution

We will isolate y on one side of the equation.

We will isolate y on one side of the equation.
Write the equation.	3x + y = 10
Subtract 3x from both sides to isolate y.	$$3x \textcolor{red}{-3x} + y= 10 \textcolor{red}{-3x}$$
Simplify.	y = 10 - 3x

Exercise $\PageIndex{15}$:

Solve the formula 7x + y = 11 for y

Answer: y = 11 - 7x

Exercise $\PageIndex{16}$:

Solve the formula 11x + y = 8 for y.

Answer: y = 8 - 11x

Example $\PageIndex{9}$:

Solve the equation 6x + 5y = 13 for y.

Solution

We will isolate y on one side of the equation.

We will isolate y on one side of the equation.
Write the equation.	6x + 5y = 13
Subtract to isolate the term with y.	$$6x + 5y \textcolor{red}{-6x} = 13 \textcolor{red}{-6x}$$
Simplify.	5y = 13 - 6x
Divide 5 to make the coefficient 1.	$$\dfrac{5y}{\textcolor{red}{5}} = \dfrac{13 - 6x}{\textcolor{red}{5}}$$
Simplify.	$$y = \dfrac{13 - 6x}{5}$$

Exercise $\PageIndex{17}$:

Solve the formula 4x + 7y = 9 for y.

Answer: $y = \frac{9-4x}{7}$

Exercise $\PageIndex{18}$:

Solve the formula 5x + 8y = 1 for y.

Answer: $y = \frac{1-5x}{8}$

ACCESS ADDITIONAL ONLINE RESOURCES

Distance = Rate x Time

Distance, Rate, Time

Simple Interest

Solving a Formula for a Specific Variable

Practice Makes Perfect

Use the Distance, Rate, and Time Formula

In the following exercises, solve.

Steve drove for $8 \dfrac{1}{2}$ hours at 72 miles per hour. How much distance did he travel?
Socorro drove for $4 \dfrac{5}{6}$ hours at 60 miles per hour. How much distance did she travel?
Yuki walked for $1 \dfrac{3}{4}$ hours at 4 miles per hour. How far did she walk?
Francie rode her bike for $2 \dfrac{1}{2}$ hours at 12 miles per hour. How far did she ride?
Connor wants to drive from Tucson to the Grand Canyon, a distance of 338 miles. If he drives at a steady rate of 52 miles per hour, how many hours will the trip take?
Megan is taking the bus from New York City to Montreal. The distance is 384 miles and the bus travels at a steady rate of 64 miles per hour. How long will the bus ride be?
Aurelia is driving from Miami to Orlando at a rate of 65 miles per hour. The distance is 235 miles. To the nearest tenth of an hour, how long will the trip take?
Kareem wants to ride his bike from St. Louis, Missouri to Champaign, Illinois. The distance is 180 miles. If he rides at a steady rate of 16 miles per hour, how many hours will the trip take?
Javier is driving to Bangor, Maine, which is 240 miles away from his current location. If he needs to be in Bangor in 4 hours, at what rate does he need to drive?
Alejandra is driving to Cincinnati, Ohio, 450 miles away. If she wants to be there in 6 hours, at what rate does she need to drive?
Aisha took the train from Spokane to Seattle. The distance is 280 miles, and the trip took 3.5 hours. What was the speed of the train?
Philip got a ride with a friend from Denver to Las Vegas, a distance of 750 miles. If the trip took 10 hours, how fast was the friend driving?

Solve a Formula for a Specific Variable

In the following exercises, use the formula. d = rt.

Solve for t: (a) when d = 350 and r = 70 (b) in general
Solve for t: (a) when d = 240 and r = 60 (b) in general
Solve for t: (a) when d = 510 and r = 60 (b) in general
Solve for t: (a) when d = 175 and r = 50 (b) in general
Solve for r: (a) when d = 204 and t = 3 (b) in general
Solve for r: (a) when d = 420 and t = 6 (b) in general
Solve for r: (a) when d = 160 and t = 2.5 (b) in general
Solve for r: (a) when d = 180 and t = 4.5 (b) in general.

In the following exercises, use the formula A = $\dfrac{1}{2}$bh.

Solve for b: (a) when A = 126 and h = 18 (b) in general
Solve for h: (a) when A = 176 and b = 22 (b) in general
Solve for h: (a) when A = 375 and b = 25 (b) in general
Solve for b: (a) when A = 65 and h = 13 (b) in general

In the following exercises, use the formula I = Prt.

Solve for the principal, P for: (a) I = $5,480, r = 4%, t = 7 years (b) in general
Solve for the principal, P for: (a) I = $3,950, r = 6%, t = 5 years (b) in general
Solve for the time, t for: (a) I = $2,376, P = $9,000, r = 4.4% (b) in general
Solve for the time, t for: (a) I = $624, P = $6,000, r = 5.2% (b) in general

In the following exercises, solve.

Solve the formula 2x + 3y = 12 for y: (a) when x = 3 (b) in general
Solve the formula 5x + 2y = 10 for y: (a) when x = 4 (b) in general
Solve the formula 3x + y = 7 for y: (a) when x = −2 (b) in general
Solve the formula 4x + y = 5 for y: (a) when x = −3 (b) in general
Solve a + b = 90 for b.
Solve a + b = 90 for a.
Solve 180 = a + b + c for a.
Solve 180 = a + b + c for c.
Solve the formula 8x + y = 15 for y.
Solve the formula 9x + y = 13 for y.
Solve the formula −4x + y = −6 for y.
Solve the formula −5x + y = −1 for y.
Solve the formula 4x + 3y = 7 for y.
Solve the formula 3x + 2y = 11 for y.
Solve the formula x − y = −4 for y.
Solve the formula x − y = −3 for y.
Solve the formula P = 2L + 2W for L.
Solve the formula P = 2L + 2W for W.
Solve the formula C = $\pi$d for d.
Solve the formula C = $\pi$d for $\pi$.
Solve the formula V = LWH for L.
Solve the formula V = LWH for H.

Everyday Math

Converting temperature While on a tour in Greece, Tatyana saw that the temperature was 40° Celsius. Solve for F in the formula C = $\dfrac{5}{9}$(F − 32) to find the temperature in Fahrenheit.
Converting temperature Yon was visiting the United States and he saw that the temperature in Seattle was 50° Fahrenheit. Solve for C in the formula F = $\dfrac{9}{5}$C + 32 to find the temperature in Celsius.

Writing Exercises

Solve the equation 2x + 3y = 6 for y: (a) when x = −3 (b) in general (c) Which solution is easier for you? Explain why.
Solve the equation 5x − 2y = 10 for x: (a) when y = 10 (b) in general (c) Which solution is easier for you? Explain why.

Self Check

(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$CNX_BMath_Figure_AppB_057.jpg$

(b) Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."

Learning Objectives

Be Prepared!

Use the Distance, Rate, and Time Formula

Definition: Distance, Rate and Time

Example \(\PageIndex{1}\):

Exercise \(\PageIndex{1}\):

Exercise \(\PageIndex{2}\):

Example \(\PageIndex{2}\):

Exercise \(\PageIndex{3}\):

Exercise \(\PageIndex{4}\):

Solve a Formula for a Specific Variable

Example \(\PageIndex{3}\):

Exercise \(\PageIndex{5}\):

Exercise \(\PageIndex{6}\):

Example \(\PageIndex{4}\):

Exercise \(\PageIndex{7}\):

Exercise \(\PageIndex{8}\):

Example \(\PageIndex{5}\):

Exercise \(\PageIndex{9}\):

Exercise \(\PageIndex{10}\):

Example \(\PageIndex{6}\):

Exercise \(\PageIndex{11}\):

Exercise \(\PageIndex{12}\):

Example \(\PageIndex{7}\):

Exercise \(\PageIndex{13}\):

Exercise \(\PageIndex{14}\):

Example \(\PageIndex{8}\):

Exercise \(\PageIndex{15}\):

Exercise \(\PageIndex{16}\):

Example \(\PageIndex{9}\):

Exercise \(\PageIndex{17}\):

Exercise \(\PageIndex{18}\):

ACCESS ADDITIONAL ONLINE RESOURCES

Practice Makes Perfect

Use the Distance, Rate, and Time Formula

Solve a Formula for a Specific Variable

Everyday Math

Writing Exercises

Self Check

Contributors and Attributions