9.12: Math Models and Geometry (Exercises)
- Last updated
- Jul 2, 2019
- Save as PDF
- Page ID
- 21764
( \newcommand{\kernel}{\mathrm{null}\,}\)
9.1 - Use a Problem Solving Strategy
Approach Word Problems with a Positive Attitude
In the following exercises, solve.
- How has your attitude towards solving word problems changed as a result of working through this chapter? Explain.
- Did the Problem Solving Strategy help you solve word problems in this chapter? Explain.
Use a Problem Solving Strategy for Word Problems
In the following exercises, solve using the problem-solving strategy for word problems. Remember to write a complete sentence to answer each question.
- Three-fourths of the people at a concert are children. If there are 87 children, what is the total number of people at the concert?
- There are 9 saxophone players in the band. The number of saxophone players is one less than twice the number of tuba players. Find the number of tuba players
- Reza was very sick and lost 15% of his original weight. He lost 27 pounds. What was his original weight?
- Dolores bought a crib on sale for $350. The sale price was 40% of the original price. What was the original price of the crib?
Solve Number Problems
In the following exercises, solve each number word problem.
- The sum of a number and three is forty-one. Find the number.
- Twice the difference of a number and ten is fifty-four. Find the number.
- One number is nine less than another. Their sum is twenty-seven. Find the numbers.
- The sum of two consecutive integers is −135. Find the numbers.
9.2 - Solve Money Applications
Solve Coin Word Problems
In the following exercises, solve each coin word problem.
- Francie has $4.35 in dimes and quarters. The number of dimes is 5 more than the number of quarters. How many of each coin does she have?
- Scott has $0.39 in pennies and nickels. The number of pennies is 8 times the number of nickels. How many of each coin does he have?
- Paulette has $140 in $5 and $10 bills. The number of $10 bills is one less than twice the number of $5 bills. How many of each does she have?
- Lenny has $3.69 in pennies, dimes, and quarters. The number of pennies is 3 more than the number of dimes. The number of quarters is twice the number of dimes. How many of each coin does he have?
Solve Ticket and Stamp Word Problems
In the following exercises, solve each ticket or stamp word problem.
- A church luncheon made $842. Adult tickets cost $10 each and children’s tickets cost $6 each. The number of children was 12 more than twice the number of adults. How many of each ticket were sold?
- Tickets for a basketball game cost $2 for students and $5 for adults. The number of students was 3 less than 10 times the number of adults. The total amount of money from ticket sales was $619. How many of each ticket were sold?
- Ana spent $4.06 buying stamps. The number of $0.41 stamps she bought was 5 more than the number of $0.26 stamps. How many of each did she buy?
- Yumi spent $34.15 buying stamps. The number of $0.56 stamps she bought was 10 less than 4 times the number of $0.41 stamps. How many of each did she buy?
9.3 - Use Properties of Angles, Triangles, and the Pythagorean Theorem
Use Properties of Angles
In the following exercises, solve using properties of angles.
- What is the supplement of a 48° angle?
- What is the complement of a 61° angle?
- Two angles are complementary. The smaller angle is 24° less than the larger angle. Find the measures of both angles.
- Two angles are supplementary. The larger angle is 45° more than the smaller angle. Find the measures of both angles.
Use Properties of Triangles
In the following exercises, solve using properties of triangles.
- The measures of two angles of a triangle are 22 and 85 degrees. Find the measure of the third angle.
- One angle of a right triangle measures 41.5 degrees. What is the measure of the other small angle?
- One angle of a triangle is 30° more than the smallest angle. The largest angle is the sum of the other angles. Find the measures of all three angles.
- One angle of a triangle is twice the measure of the smallest angle. The third angle is 60° more than the measure of the smallest angle. Find the measures of all three angles.
In the following exercises, ΔABC is similar to ΔXYZ. Find the length of the indicated side.
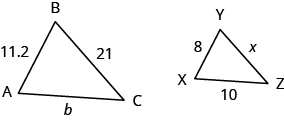
- side x
- side b
Use the Pythagorean Theorem
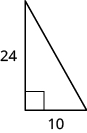
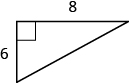
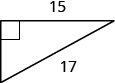
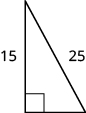
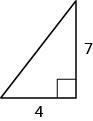
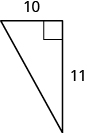
In the following exercises, use the Pythagorean Theorem to find the length of the missing side. Round to the nearest tenth, if necessary
In the following exercises, solve. Approximate to the nearest tenth, if necessary.
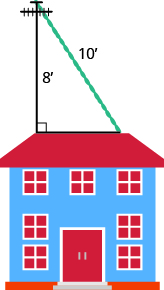
- Sergio needs to attach a wire to hold the antenna to the roof of his house, as shown in the figure. The antenna is 8 feet tall and Sergio has 10 feet of wire. How far from the base of the antenna can he attach the wire?
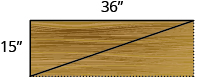
- Seong is building shelving in his garage. The shelves are 36 inches wide and 15 inches tall. He wants to put a diagonal brace across the back to stabilize the shelves, as shown. How long should the brace be?
9.4 - Use Properties of Rectangles, Triangles, and Trapezoids
Understand Linear, Square, Cubic Measure
In the following exercises, would you measure each item using linear, square, or cubic measure?
- amount of sand in a sandbag
- height of a tree
- size of a patio
- length of a highway
In the following exercises, find (a) the perimeter (b) the area of each figure
Use Properties of Rectangles
In the following exercises, find the (a) perimeter (b) area of each rectangle
- The length of a rectangle is 42 meters and the width is 28 meters.
- The length of a rectangle is 36 feet and the width is 19 feet.
- A sidewalk in front of Kathy’s house is in the shape of a rectangle 4 feet wide by 45 feet long.
- A rectangular room is 16 feet wide by 12 feet long.
In the following exercises, solve.
- Find the length of a rectangle with perimeter of 220 centimeters and width of 85 centimeters.
- Find the width of a rectangle with perimeter 39 and length 11.
- The area of a rectangle is 2356 square meters. The length is 38 meters. What is the width?
- The width of a rectangle is 45 centimeters. The area is 2700 square centimeters. What is the length?
- The length of a rectangle is 12 centimeters more than the width. The perimeter is 74 centimeters. Find the length and the width.
- The width of a rectangle is 3 more than twice the length. The perimeter is 96 inches. Find the length and the width.
Use Properties of Triangles
In the following exercises, solve using the properties of triangles.
- Find the area of a triangle with base 18 inches and height 15 inches.
- Find the area of a triangle with base 33 centimeters and height 21 centimeters.
- A triangular road sign has base 30 inches and height 40 inches. What is its area?
- If a triangular courtyard has sides 9 feet and 12 feet and the perimeter is 32 feet, how long is the third side?
- A tile in the shape of an isosceles triangle has a base of 6 inches. If the perimeter is 20 inches, find the length of each of the other sides.
- Find the length of each side of an equilateral triangle with perimeter of 81 yards.
- The perimeter of a triangle is 59 feet. One side of the triangle is 3 feet longer than the shortest side. The third side is 5 feet longer than the shortest side. Find the length of each side.
- One side of a triangle is three times the smallest side. The third side is 9 feet more than the shortest side. The perimeter is 39 feet. Find the lengths of all three sides.
Use Properties of Trapezoids
In the following exercises, solve using the properties of trapezoids.
- The height of a trapezoid is 8 feet and the bases are 11 and 14 feet. What is the area?
- The height of a trapezoid is 5 yards and the bases are 7 and 10 yards. What is the area?
- Find the area of the trapezoid with height 25 meters and bases 32.5 and 21.5 meters.
- A flag is shaped like a trapezoid with height 62 centimeters and the bases are 91.5 and 78.1 centimeters. What is the area of the flag?
9.5 - Solve Geometry Applications: Circles and Irregular Figures
Use Properties of Circle
s In the following exercises, solve using the properties of circles. Round answers to the nearest hundredth.
- A circular mosaic has radius 3 meters. Find the (a) circumference (b) area of the mosaic
- A circular fountain has radius 8 feet. Find the (a) circumference (b) area of the fountain
- Find the diameter of a circle with circumference 150.72 inches.
- Find the radius of a circle with circumference 345.4 centimeters
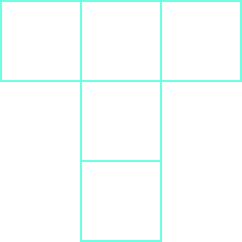
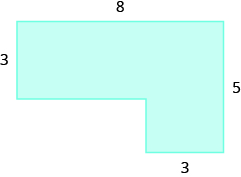
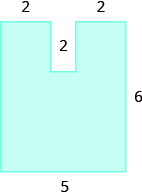
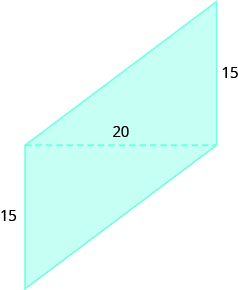
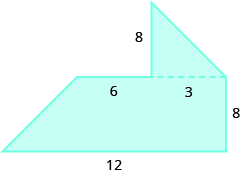
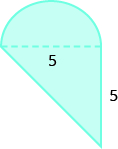
Find the Area of Irregular Figures
In the following exercises, find the area of each shaded region.
9.6 - Solve Geometry Applications: Volume and Surface Area
Find Volume and Surface Area of Rectangular Solids
In the following exercises, find the (a) volume (b) surface area of the rectangular solid
- a rectangular solid with length 14 centimeters, width 4.5 centimeters, and height 10 centimeters
- a cube with sides that are 3 feet long
- a cube of tofu with sides 2.5 inches
- a rectangular carton with length 32 inches, width 18 inches, and height 10 inches
Find Volume and Surface Area of Spheres
In the following exercises, find the (a) volume (b) surface area of the sphere.
- a sphere with radius 4 yards
- a sphere with radius 12 meters
- a baseball with radius 1.45 inches
- a soccer ball with radius 22 centimeters
Find Volume and Surface Area of Cylinders
In the following exercises, find the (a) volume (b) surface area of the cylinder
- a cylinder with radius 2 yards and height 6 yards
- a cylinder with diameter 18 inches and height 40 inches
- a juice can with diameter 8 centimeters and height 15 centimeters
- a cylindrical pylon with diameter 0.8 feet and height 2.5 feet
Find Volume of Cones
In the following exercises, find the volume of the cone.
- a cone with height 5 meters and radius 1 meter
- a cone with height 24 feet and radius 8 feet
- a cone-shaped water cup with diameter 2.6 inches and height 2.6 inches
- a cone-shaped pile of gravel with diameter 6 yards and height 5 yards
9.7 - Solve a Formula for a Specific Variable
Use the Distance, Rate, and Time Formula
In the following exercises, solve using the formula for distance, rate, and time.
- A plane flew 4 hours at 380 miles per hour. What distance was covered?
- Gus rode his bike for 112 hours at 8 miles per hour. How far did he ride?
- Jack is driving from Bangor to Portland at a rate of 68 miles per hour. The distance is 107 miles. To the nearest tenth of an hour, how long will the trip take?
- Jasmine took the bus from Pittsburgh to Philadelphia. The distance is 305 miles and the trip took 5 hours. What was the speed of the bus?
Solve a Formula for a Specific Variable
In the following exercises, use the formula d = rt.
- Solve for t: (a) when d = 403 and r = 65 (b) in general
- Solve for r: (a) when d = 750 and t = 15 (b) in general
In the following exercises, use the formula A = 12bh.
- Solve for b: (a) when A = 416 and h = 32 (b) in general
- Solve for h: (a) when A = 48 and b = 8 (b) in general
In the following exercises, use the formula I = Prt.
- Solve for the principal, P, for: (a) I = $720, r = 4%, t = 3 years (b) in general
- Solve for the time, t for: (a) I = $3630, P = $11,000, r = 5.5% (b) in general
In the following exercises, solve.
- Solve the formula 6x + 5y = 20 for y: (a) when x = 0 (b) in general
- Solve the formula 2x + y = 15 for y: (a) when x = −5 (b) in general
- Solve a + b = 90 for a.
- Solve 180 = a + b + c for a.
- Solve the formula 4x + y = 17 for y.
- Solve the formula −3x + y = −6 for y.
- Solve the formula P = 2L + 2W for W.
- Solve the formula V = LWH for H.
- Describe how you have used two topics from this chapter in your life outside of math class during the past month.
PRACTICE TEST
- Four-fifths of the people on a hike are children. If there are 12 children, what is the total number of people on the hike?
- The sum of 13 and twice a number is −19. Find the number.
- One number is 3 less than another number. Their sum is 65. Find the numbers.
- Bonita has $2.95 in dimes and quarters in her pocket. If she has 5 more dimes than quarters, how many of each coin does she have?
- At a concert, $1600 in tickets were sold. Adult tickets were $9 each and children’s tickets were $4 each. If the number of adult tickets was 30 fewer than twice the number of children’s tickets, how many of each kind were sold?
- Find the complement of a 52° angle.
- The measure of one angle of a triangle is twice the measure of the smallest angle. The measure of the third angle is 14 more than the measure of the smallest angle. Find the measures of all three angles.
- The perimeter of an equilateral triangle is 145 feet. Find the length of each side.
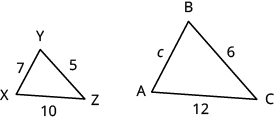
- ΔABC is similar to ΔXYZ. Find the length of side c.
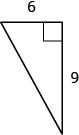
- Find the length of the missing side. Round to the nearest tenth, if necessary.
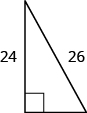
- Find the length of the missing side. Round to the nearest tenth, if necessary.
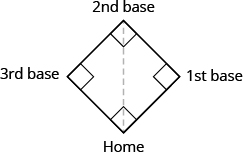
- A baseball diamond is shaped like a square with sides 90 feet long. How far is it from home plate to second base, as shown?
- The length of a rectangle is 2 feet more than five times the width. The perimeter is 40 feet. Find the dimensions of the rectangle.
- A triangular poster has base 80 centimeters and height 55 centimeters. Find the area of the poster.
- A trapezoid has height 14 inches and bases 20 inches and 23 inches. Find the area of the trapezoid.
- A circular pool has diameter 90 inches. What is its circumference? Round to the nearest tenth.
- Find the area of the shaded region. Round to the nearest tenth.
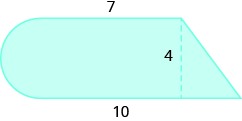
- Find the volume of a rectangular room with width 12 feet, length 15 feet, and height 8 feet.
- A coffee can is shaped like a cylinder with height 7 inches and radius 5 inches. Find (a) the surface area and (b) the volume of the can. Round to the nearest tenth.
- A traffic cone has height 75 centimeters. The radius of the base is 20 centimeters. Find the volume of the cone. Round to the nearest tenth.
- Leon drove from his house in Cincinnati to his sister’s house in Cleveland. He drove at a uniform rate of 63 miles per hour and the trip took 4 hours. What was the distance?
- The Catalina Express takes 112 hours to travel from Long Beach to Catalina Island, a distance of 22 miles. To the nearest tenth, what is the speed of the boat?
- Use the formula I = Prt to solve for the principal, P, for: (a) I = $1380, r = 5%, t = 3 years (b) in general
- Solve the formula A = 12bh for h: (a) when A = 1716 and b = 66 (b) in general
- Solve x + 5y = 14 for y.
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."