5.8: Applications
- Page ID
- 104867
Use Systems in Applications
Systems can be very useful for solving word problems involving several variables. Here is an example of a problem you will see in the near future.
1 pound of cereal A contains 6g of potassium and 2g of calcium. 1 pound of cereal B contains 7g of potassium and 4g of calcium. How many pounds of each cereal is needed to have a mixture of 51g of potassium and 22g of calcium?
Solution
| Write this word problem as a system of equations |
We have "a" pounds of cereal A and that contains \(6\cdot a\) grams of potassium. We have "b" pounds of cereal B and that contains \(7\cdot b\) grams of potassium. Combining these, we should get 51 g of potassium. So that's \(6a+7b=51\). Likewise, We have "a" pounds of cereal A and that contains \(2\cdot a\) grams of calcium. We have "b" pounds of cereal B and that contains \(4\cdot b\) grams of calcium. Combining these, we should get 22 g of potassium. So that's \(2a+4b=22\). \( \begin{align*} &6a+7b=51\\ &2a+4b=22 \end{align*}\) |
| Solve the system of equations using either substitution or elimination. We will be using elimination for this. |
\( \begin{align*} &6a+7b=51\\ &2a+4b=22 \Rightarrow 3(2a+4b)=3(22)\\ \\ &6a+7b=51\\ & 6a+12b=66\\ &\text{subtract the bottom from the top} \\ &5b=15\Rightarrow b=3\\ &2a+4(3)=22 \Rightarrow a=5 \end{align*}\) |
| State the answer | We need 5 pounds of cereal A and 3 pounds of cereal B. |
Let's do some more examples.
1 pound of cereal A contains 10g of potassium and 1g of calcium. 1 pound of cereal B contains 4g of potassium and 5g of calcium. How many pounds of each cereal is needed to have a mixture of 44g of potassium and 32g of calcium?
- Answer
-
We need 2 pounds of cereal A and 6 pounds of cereal B.
A pound of cereal A contains 14g of potassium and 3g of calcium. 1 pound of cereal B contains 7g of potassium and 4g of calcium. How many pounds of each cereal is needed to have a mixture of 70g of potassium and 25g of calcium?
- Answer
-
We need 3 pounds of cereal A and 4 pounds of cereal B.
A pound of cereal A contains 8g of potassium and 3g of calcium. 1 pound of cereal B contains 3g of potassium and 2g of calcium. How many pounds of each cereal is needed to have a mixture of 77g of potassium and 22g of calcium?
- Answer
-
We need 4 pounds of cereal A and 5 pounds of cereal B.
Rates in Applications
Suppose we have two people painting a house. Person A takes 2 hours to paint a house and Person B takes 3 hours to paint a house, how long will it take for them to paint a house working together? The solution to this isn't immediately obvious so lets try a simpler problem.
Say Person A and B both take 2 hours to paint a house. Intuitively, we want to say they take 1 hour to paint a house if they work together but why? Well both of them work at a rate of half a house per hour so if we give Person A and Person B "x" amount of hours, add their progress together, we should get 1 house. So \(x\dfrac{1}{2}+x\dfrac{1}{2}=1\). We can add fractions, so we see that the answer is x=1 hour.
Let's take another intuitive example. Say both are painting a shed and both take an hour working separately, what about together? Intuitively we want to say that they will be done in half an hour. Thinking about it in rates, we get \(x(1)+x(1)=1\Rightarrow 2x=1\Rightarrow x=\dfrac{1}{2}\).
Okay, we are ready to come back to the original problem.
Suppose we have two people painting a house. Person A takes 2 hours to paint a house and Person B takes 3 hours to paint a house, how long will it take for them to paint a house working together?
Solution
Person A works at a rate of \(\frac{1}{2}\) house per hour. Person B works at a rate of \(\frac{1}{3}\).
\(x\dfrac{1}{2}+x\dfrac{1}{3}=1\)
\(x\dfrac{3}{6}+x\dfrac{2}{6}=1\)
\(x\dfrac{5}{6}=1\)
\(x=\dfrac{6}{5}\)
So it will take \(\dfrac{6}{5}\) hours.
Let's try some more examples.
Suppose we have two people painting a house. Person A takes 5 hours to paint a house and Person B takes 3 hours to paint a house, how long will it take for them to paint a house working together?
- Answer
-
\(\dfrac{15}{8}\) hours
Suppose we have two people painting a house. Person A takes 5 hours to paint a house and Person B takes 4 hours to paint a house, how long will it take for them to paint a house working together?
- Answer
-
\(\dfrac{20}{9}\) hours
Suppose we have two people painting a house. Person A takes 6 hours to paint a house and Person B takes 3 hours to paint a house, how long will it take for them to paint a house working together?
- Answer
-
2 hours
Use Radicals in Applications
As you progress through your college courses, you’ll encounter formulas that include radicals in many disciplines. We will modify our Problem Solving Strategy for Geometry Applications slightly to give us a plan for solving applications with formulas from any discipline.
Use a Problem Solving Strategy for Applications With Formulas
- Read the problem and make sure all the words and ideas are understood. When appropriate, draw a figure and label it with the given information.
- Identify what we are looking for.
- Name what we are looking for by choosing a variable to represent it.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
One application of radicals has to do with the effect of gravity on falling objects. The formula allows us to determine how long it will take a fallen object to hit the gound.
Definition \(\PageIndex{2}\)
Falling Objects
On Earth, if an object is dropped from a height of \(h\) feet, the time in seconds it will take to reach the ground is found by using the formula
\(t=\frac{\sqrt{h}}{4}\)
For example, if an object is dropped from a height of \(64\) feet, we can find the time it takes to reach the ground by substituting \(h=64\) into the formula.
 |
|
 |
|
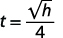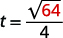| Take the square root of \(64\). |  |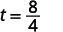
| Simplify the fraction. |  |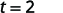
It would take \(2\) seconds for an object dropped from a height of \(64\) feet to reach the ground.
Marissa dropped her sunglasses from a bridge \(400\) feet above a river. Use the formula \(t=\frac{\sqrt{h}}{4}\) to find how many seconds it took for the sunglasses to reach the river.
Solution:
| Step 1: Read the problem. | |
| Step 2: Identify what we are looking. | The time it takes for the sunglasses to reach the river. |
| Step 3: Name what we are looking. | Let (t=\) time. |
| Step 4: Translate into an equation by writing the appropriate formula. Substitute in the given information. |  |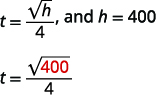
| Step 5: Solve the equation. |  |
 |
|
| Step 6: Check the answer in the problem and make sure it makes sense. |  |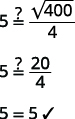
| Does \(5\) seconds seem like a reasonable length of time? | Yes. |
| Step 7: Answer the equation. | It will take \(5\) seconds for the sunglasses to reach the river. |
A helicopter dropped a rescue package from a height of \(1,296\) feet. Use the formula \(t=\frac{\sqrt{h}}{4}\) to find how many seconds it took for the package to reach the ground.
- Answer
-
\(9\) seconds
A window washer dropped a squeegee from a platform \(196\) feet above the sidewalk. Use the formula \(t=\frac{\sqrt{h}}{4}\) to find how many seconds it took for the squeegee to reach the sidewalk.
- Answer
-
\(3.5\) seconds
Police officers investigating car accidents measure the length of the skid marks on the pavement. Then they use square roots to determine the speed, in miles per hour, a car was going before applying the brakes.
Definition \(\PageIndex{3}\)
Skid Marks and Speed of a Car
If the length of the skid marks is \(d\) feet, then the speed, \(s\), of the car before the brakes were applied can be found by using the formula
\(s=\sqrt{24 d}\)
After a car accident, the skid marks for one car measured \(190\) feet. Use the formula \(s=\sqrt{24d}\) to find the speed of the car before the brakes were applied. Round your answer to the nearest tenth.
Solution:
| Step 1: Read the problem. | |
| Step 2: Identify what we are looking for. | The speed of a car. |
| Step 3: Name what we are looking for. | Let \(s=\) the speed. |
| Step 4: Translate into an equation by writing the appropriate formula. Substitute in the given information. |  |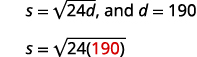
| Step 5: Solve the equation. |  |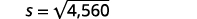
 |
|
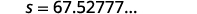| Round to \(1\) decimal place. |  |
 |
|
| The speed of the car before the brakes were applied was \(67.5\) miles per hour. |
An accident investigator measured the skid marks of the car. The length of the skid marks was \(76\) feet. Use the formula \(s=\sqrt{24d}\) to find the speed of the car before the brakes were applied. Round your answer to the nearest tenth.
- Answer
-
\(42.7\) feet
The skid marks of a vehicle involved in an accident were \(122\) feet long. Use the formula \(s=\sqrt{24d}\) to find the speed of the vehicle before the brakes were applied. Round your answer to the nearest tenth.
- Answer
-
\(54.1\) feet
Solve Maximum and Minimum Applications
Knowing that the vertex of a parabola is the lowest or highest point of the parabola gives us an easy way to determine the minimum or maximum value of a quadratic function. The y-coordinate of the vertex is the minimum value of a parabola that opens upward. It is the maximum value of a parabola that opens downward. See Figure 9.6.124.
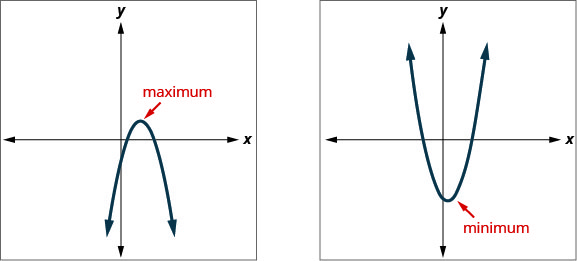
Minimum or Maximum Values of a Quadratic Function
The y-coordinate of the vertex of the graph of a quadratic function is the
- minimum value of the quadratic equation if the parabola opens upward.
- maximum value of the quadratic equation if the parabola opens downward.
Find the minimum or maximum value of the quadratic function \(f(x)=x^{2}+2 x-8\).
Solution:
| \(f(x)=x^{2}+2 x-8\) | |
| Since \(a\) is positive, the parabola opens upward. The quadratic equation has a minimum. | |
| Find the equation of the axis of symmetry. | \(x=-\frac{b}{2 a}\) |
| \(x=-\frac{2}{2 \times 1}\) | |
| \(x=-1\) | |
| The equation of the axis of symmetry is \(x=-1\). | |
| The vertex is on the line \(x=-1\). | \(f(x)=x^{2}+2 x-8\) |
| Find \(f(-1)\). |  |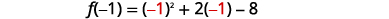
| \(f(-1)=1-2-8\) | |
| \(f(-1)=-9\) | |
| The vertex is \((-1,-9)\). | |
| Since the parabola has a minimum, the \(y\)-coordinate of the vertex is the minimum \(y\)-value of the quadratic equation. The minimum value of the quadratic is \(-9\) and it occurs when \(x=-1\). | |
 |
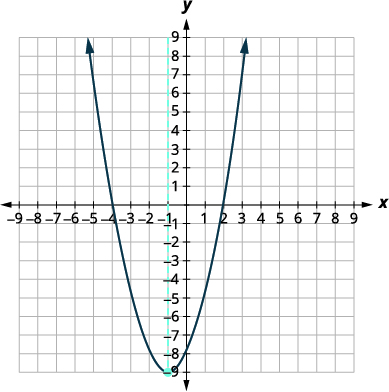Show the graph to verify the result.
Find the maximum or minimum value of the quadratic function \(f(x)=x^{2}-8 x+12\).
- Answer
-
The minimum value of the quadratic function is \(−4\) and it occurs when \(x=4\).
Find the maximum or minimum value of the quadratic function \(f(x)=-4 x^{2}+16 x-11\).
- Answer
-
The maximum value of the quadratic function is \(5\) and it occurs when \(x=2\).
We have used the formula
\(h(t)=-16 t^{2}+v_{0} t+h_{0}\)
to calculate the height in feet, \(h\), of an object shot upwards into the air with initial velocity, \(v_{0}\), after \(t\) seconds .
This formula is a quadratic function, so its graph is a parabola. By solving for the coordinates of the vertex \((t,h)\), we can find how long it will take the object to reach its maximum height. Then we can calculate the maximum height.
The quadratic equation \(h(t)=-16 t^{2}+176 t+4\) models the height of a volleyball hit straight upwards with velocity \(176\) feet per second from a height of \(4\) feet.
- How many seconds will it take the volleyball to reach its maximum height?
- Find the maximum height of the volleyball.
Solution:
\(h(t)=-16 t^{2}+176 t+4\)
Since \(a\) is negative, the parabola opens downward. The quadratic function has a maximum.
a. Find the equation of the axis of symmetry.
\(\begin{array}{l}{t=-\frac{b}{2 a}} \\ {t=-\frac{176}{2(-16)}} \\ {t=5.5}\end{array}\)
The equation of the axis of symmetry is \(t=5.5\).
The vertex is on the line \(t=5.5\).
The maximum occurs when \(t=5.5\) seconds.
b. Find \(h(5.5)\).
\(\begin{array}{l}{h(t)=-16 t^{2}+176 t+4} \\ {h(t)=-16(5.5)^{2}+176(5.5)+4}\end{array}\)
Use a calculator to simplify.
\(h(t)=488\)
The vertex is \((5.5,488)\).
Since the parabola has a maximum, the \(h\)-coordinate of the vertex is the maximum value of the quadratic function.
The maximum value of the quadratic is \(488\) feet and it occurs when \(t=5.5\) seconds.
After \(5.5\) seconds, the volleyball will reach its maximum height of \(488\) feet.
Solve, rounding answers to the nearest tenth.
The quadratic function \(h(t)=-16 t^{2}+128 t+32\) is used to find the height of a stone thrown upward from a height of \(32\) feet at a rate of \(128\) ft/sec. How long will it take for the stone to reach its maximum height? What is the maximum height?
- Answer
-
It will take \(4\) seconds for the stone to reach its maximum height of \(288\) feet.
A path of a toy rocket thrown upward from the ground at a rate of \(208\) ft/sec is modeled by the quadratic function of \(h(t)=-16 t^{2}+208 t\). When will the rocket reach its maximum height? What will be the maximum height?
- Answer
-
It will take \(6.5\) seconds for the rocket to reach its maximum height of \(676\) feet.