13.9.3: Add and Subtract Rational Expressions with a Common Denominator
- Last updated
- Aug 13, 2020
- Save as PDF
- Page ID
- 46300
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Add rational expressions with a common denominator
- Subtract rational expressions with a common denominator
- Add and subtract rational expressions whose denominators are opposites
Note
Before you get started, take this readiness quiz.
If you miss a problem, go back to the section listed and review the material.
- Add: y3+93.
If you missed this problem, review Exercise 1.7.1. - Subtract: 10x−2x.
If you missed this problem, review Exercise 1.7.7. - Factor completely: 8n5−20n3.
If you missed this problem, review Exercise 7.5.1. - Factor completely: 45a3−5ab2.
If you missed this problem, review Exercise 7.5.10.
Add Rational Expressions with a Common Denominator
What is the first step you take when you add numerical fractions? You check if they have a common denominator. If they do, you add the numerators and place the sum over the common denominator. If they do not have a common denominator, you find one before you add.
It is the same with rational expressions. To add rational expressions, they must have a common denominator. When the denominators are the same, you add the numerators and place the sum over the common denominator.
Definition: RATIONAL EXPRESSION ADDITION
If p, q, and r are polynomials where r≠0, then
pr+qr=p+qr
To add rational expressions with a common denominator, add the numerators and place the sum over the common denominator.
We will add two numerical fractions first, to remind us of how this is done.
Example 13.9.3.1
Add: 518+718.
- Answer
-
518+718 The fractions have a common denominator, so add the numerators and place the sum over the common denominator. 5+718 Add in the numerator. 1218 Factor the numerator and denominator to show the common factors. 6·26·3 Simplify. 23
Example 13.9.3.2
Add: 716+516.
- Answer
-
34
Example 13.9.3.3
Add: 310+110.
- Answer
-
25
Remember, we do not allow values that would make the denominator zero. What value of yy should be excluded in the next example?
Example 13.9.3.4
Add: 3y4y−3+74y−3.
- Answer
-
3y4y−3+74y−3. The fractions have a common denominator, so add the numerators and place the sum over the common denominator. 3y+74y−3 The numerator and denominator cannot be factored. The fraction is simplified.
Example 13.9.3.5
Add: 5x2x+3+22x+3.
- Answer
-
5x+22x+3.
Example 13.9.3.6
Add: xx−2+1x−2.
- Answer
-
x+1x−2
Example 13.9.3.7
Add: 7x+12x+3+x2x+3.
- Answer
-
7x+12x+3+x2x+3 The fractions have a common denominator, so add the numerators and place the sum over the common denominator. 7x+12+x2x+3 Write the degrees in descending order. x2+7x+12x+3 Factor the numerator. (x+3)(x+4)x+3 Simplify. x+4
Example 13.9.3.8
Add: 9x+14x+7+x2x+7.
- Answer
-
x+2
Example 13.9.3.9
Add: x2+8xx+5+15x+5.
- Answer
-
x+3
Subtract Rational Expressions with a Common Denominator
To subtract rational expressions, they must also have a common denominator. When the denominators are the same, you subtract the numerators and place the difference over the common denominator.
Definition: RATIONAL EXPRESSION SUBTRACTION
If p, q, and r are polynomials where r≠0
pr−qr=p−qr
To subtract rational expressions, subtract the numerators and place the difference over the common denominator.
We always simplify rational expressions. Be sure to factor, if possible, after you subtract the numerators so you can identify any common factors.
Example 13.9.3.10
Subtract: n2n−10−100n−10.
- Answer
-
n2n−10−100n−10 The fractions have a common denominator, so add the numerators and place the sum over the common denominator. n2−100n−10 Factor the numerator. (n−10)(n+10)n−10 Simplify. n+10
Example 13.9.3.11
Subtract: x2x+3−9x+3.
- Answer
-
x−3
Example 13.9.3.12
Subtract: 4x22x−5−252x−5.
- Answer
-
2x+5
Be careful of the signs when you subtract a binomial!
Example 13.9.3.13
Subtract: y2y−6−2y+24y−6.
- Answer
-
y2y−6−2y+24y−6 The fractions have a common denominator, so add the numerators and place the sum over the common denominator. y2−(2y+24)y−6 Distribute the sign in the numerator. y2−2y−24y−6 Factor the numerator. (y−6)(y+4)y−6 Simplify. y+4
Example 13.9.3.14
Subtract: n2n−4−n+12n−4.
- Answer
-
n+3
Example 13.9.3.15
Subtract: y2y−1−9y−8y−1.
- Answer
-
y−8
Example 13.9.3.16
Subtract: 5x2−7x+3x2−3x−18−4x2+x−9x2−3x−18.
- Answer
-
5x2−7x+3x2−3x+18−4x2+x−9x2−3x+18 The fractions have a common denominator, so add the numerators and place the sum over the common denominator. 5x2−7x+3−(4x2+x−9)x2−3x+18 Distribute the sign in the numerator. 5x2−7x+3−4x2−x+9x2−3x+18 Combine like terms. x2−8x+12x2−3x+18 Factor the numerator and the denominator. (x−2)(x−6)(x+3)(x−6) Simplify. x−2x+3
Example 13.9.3.17
Subtract: 4x2−11x+8x2−3x+2−3x2+x−3x2−3x+2.
- Answer
-
x−11x−2
Example 13.9.3.18
Subtract: 6x2−x+20x2−81−5x2+11x−7x2−81.
- Answer
-
x−3x+9
Add and Subtract Rational Expressions whose Denominators are Opposites
When the denominators of two rational expressions are opposites, it is easy to get a common denominator. We just have to multiply one of the fractions by −1−1
Let’s see how this works.
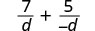 |
|
| Multiply the second fraction by −1−1. | 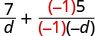 |
| The denominators are the same. | 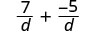 |
| Simplify. | 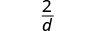 |
Example 13.9.3.19
Add: 4u−13u−1+u1−3u.
- Answer
-
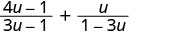
Multiply the second fraction by −1−1. 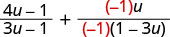
Simplify the second fraction. 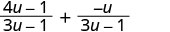
The denominators are the same. Add the numerators. 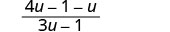
Simplify. 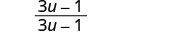
Simplify. 
Example 13.9.3.20
Add: 8x−152x−5+2x5−2x.
- Answer
-
3
Example 13.9.3.21
Add: 6y2+7y−104y−7+2y2+2y+117−4y.
- Answer
-
y+3
Example 13.9.3.22
Subtract: m2−6mm2−1−3m+21−m2.
- Answer
-
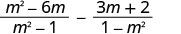
Multiply the second fraction by −1−1. 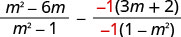
Simplify the second fraction. 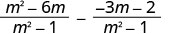
The denominators are the same. Subtract the numerators. 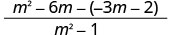
Distribute. m2−6m+3m+2m2−1 Combine like terms. 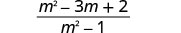
Factor the numerator and denominator. 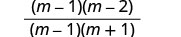
Simplify by removing common factors. 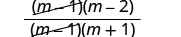
Simplify. 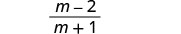
Example 13.9.3.23
Subtract: y2−5yy2−4−6y−64−y2.
- Answer
-
y+3y+2
Example 13.9.3.24
Subtract: 2n2+8n−1n2−1−n2−7n−11−n2.
- Answer
-
3n−2n−1
Key Concepts
- Rational Expression Addition
- If p, q, and r are polynomials where r≠0, then
pr+qr=p+qr
- To add rational expressions with a common denominator, add the numerators and place the sum over the common denominator.
- If p, q, and r are polynomials where r≠0, then
- Rational Expression Subtraction
- If p, q, and r are polynomials where r≠0
pr−qr=p−qr
- To subtract rational expressions, subtract the numerators and place the difference over the common denominator.
- If p, q, and r are polynomials where r≠0


