17.2: Simplify Expressions with Roots

Learning Objectives

By the end of this section, you will be able to:

• Simplify expressions with roots
• Estimate and approximate roots
• Simplify variable expressions with roots

Before you get started, take this readiness quiz.

1. Simplify: a. $(−9)^{2}$ b. $-9^{2}$ c. $(−9)^{3}$
   If you missed this problem, review Example 2.21.
2. Round $3.846$ to the nearest hundredth.
   If you missed this problem, review Example 1.34.
3. Simplify: a. $x^{3} \cdot x^{3}$ b. $y^{2} \cdot y^{2} \cdot y^{2}$ c. $z^{3} \cdot z^{3} \cdot z^{3} \cdot z^{3}$
   If you missed this problem, review Example 5.12.

Simplify Expressions with Roots

In Foundations, we briefly looked at square roots. Remember that when a real number $n$ is multiplied by itself, we write $n^{2}$ and read it '$n^{2}$ squared’. This number is called the square of $n$, and $n$ is called the square root. For example,

$13^{2}$ is read "$13$ squared"

$169$ is called the square of $13$, since $13^{2}=169$

$13$ is a square root of $169$

Definition $\PageIndex{1}$: Square and Square Root of a Number

Square

If $n^{2}=m$, then $m$ is the square of $n$.

Square Root

If $n^{2}=m$, then $n$ is a square root of $m$.

Notice $(−13)^{2} = 169$ also, so $−13$ is also a square root of $169$. Therefore, both $13$ and $−13$ are square roots of $169$.

So, every positive number has two square roots—one positive and one negative. What if we only wanted the positive square root of a positive number? We use a radical sign, and write, $\sqrt{m}$, which denotes the positive square root of $m$. The positive square root is also called the principal square root.

We also use the radical sign for the square root of zero. Because $0^{2}=0, \sqrt{0}=0$. Notice that zero has only one square root.

Definition $\PageIndex{2}$: Square Root Notation

$\sqrt{m}$ is read "the square root of $m$."

If $n^{2}=m$, then $n=\sqrt{m}$, for $n\geq 0$.

$$\color{cyan} \text{radical sign} \longrightarrow \color{black} \sqrt{m} \color{cyan} \longleftarrow \text{radicand} \nonumber$$

Figure 8.1.1

We know that every positive number has two square roots and the radical sign indicates the positive one. We write $\sqrt{169}=13$. If we want to find the negative square root of a number, we place a negative in front of the radical sign. For example, $-\sqrt{169}=-13$.

Example $\PageIndex{1}$

Simplify:

1. $\sqrt{144}$
2. $-\sqrt{289}$

Solution:

a.

$\sqrt{144}$

Since $12^{2}=144$.

$12$

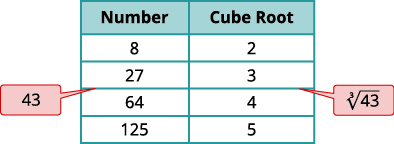
b.

$-\sqrt{289}$

Since $17^{2}=289$ and the negative is in front of the radical sign.

$-17$

Exercise $\PageIndex{1}$

Simplify:

1. $-\sqrt{64}$
2. $\sqrt{225}$

Answer

1. $-8$
2. $15$

Exercise $\PageIndex{2}$

Simplify:

1. $\sqrt{100}$
2. $-\sqrt{121}$

Answer

1. $10$
2. $-11$

Can we simplify $-\sqrt{49}$? Is there a number whose square is $-49$?

$($___$)^{2}=-49$

Any positive number squared is positive. Any negative number squared is positive. There is no real number equal to $\sqrt{-49}$. The square root of a negative number is not a real number.

Example $\PageIndex{2}$

Simplify:

1. $\sqrt{-196}$
2. $-\sqrt{64}$

Solution:

a.

$\sqrt{-196}$

There is no real number whose square is $-196$.

$\sqrt{-196}$ is not a real number.

b.

$-\sqrt{64}$

The negative is in front of the radical.

$-8$

Exercise $\PageIndex{3}$

Simplify:

1. $\sqrt{-169}$
2. $-\sqrt{81}$

Answer

1. not a real number
2. $-9$

Exercise $\PageIndex{4}$

Simplify:

1. $-\sqrt{49}$
2. $\sqrt{-121}$

Answer

1. $-7$
2. not a real number

So far we have only talked about squares and square roots. Let’s now extend our work to include higher powers and higher roots.

Let’s review some vocabulary first.

$\begin{array}{ll}{\text { We write: }} & {\text { We say: }} \\ {n^{2}} & {n \text { squared }} \\ {n^{3}} & {n \text { cubed }} \\ {n^{4}} & {n \text { to the fourth power }} \\ {n^{5}} & {n \text { to the fifth power }}\end{array}$

The terms ‘squared’ and ‘cubed’ come from the formulas for area of a square and volume of a cube.

It will be helpful to have a table of the powers of the integers from $−5$ to $5$. See Figure 8.1.2

Figure 8.1.2

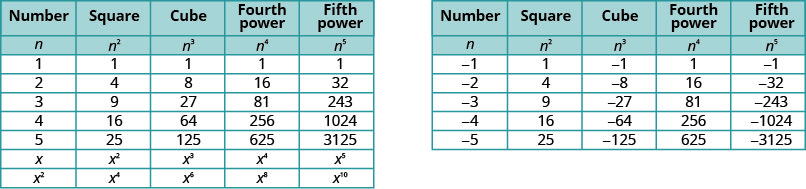
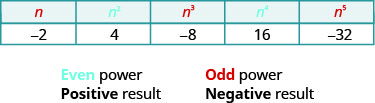
Notice the signs in the table. All powers of positive numbers are positive, of course. But when we have a negative number, the even powers are positive and the odd powers are negative. We’ll copy the row with the powers of $−2$ to help you see this.

Figure 8.1.3

We will now extend the square root definition to higher roots.

Definition $\PageIndex{3}$: N^th Root of a Number

If $b^{n}=a$, then $b$ is an $n^{th}$ root of $a$.

The principal $n^{th}$ root of $a$ is written $\sqrt[n]{a}$.

The $n$ is called the index of the radical.

Just like we use the word ‘cubed’ for $b^{3}$, we use the term ‘cube root’ for $\sqrt[3]{a}$.

We can refer to Figure 8.1.2 to help find higher roots.

$\begin{aligned} 4^{3} &=64 & \sqrt[3]{64}&=4 \\ 3^{4} &=81 & \sqrt[4]{81}&=3 \\(-2)^{5} &=-32 & \sqrt[5]{-32}&=-2 \end{aligned}$

Could we have an even root of a negative number? We know that the square root of a negative number is not a real number. The same is true for any even root. Even roots of negative numbers are not real numbers. Odd roots of negative numbers are real numbers.

Properties of $\sqrt[n]{a}$

When $n$ is an even number and

• $a \geq 0$, then $\sqrt[n]{a}$ is a real number.
• $a<0$, then $\sqrt[n]{a}$ is not a real number.

When $n$ is an odd number, $\sqrt[n]{a}$ is a real number for all the values of $a$.

We will apply these properties in the next two examples.

Example $\PageIndex{3}$

Simplify:

1. $\sqrt[3]{64}$
2. $\sqrt[4]{81}$
3. $\sqrt[5]{32}$

Solution:

a.

$\sqrt[3]{64}$

Since $4^{3}=64$.

$4$

b.

$\sqrt[4]{81}$

Since $(3)^{4}=81$.

$3$

c.

$\sqrt[5]{32}$

Since $(2)^{5}=32$.

$2$

Exercise $\PageIndex{5}$

Simplify:

1. $\sqrt[3]{27}$
2. $\sqrt[4]{256}$
3. $\sqrt[5]{243}$

Answer

1. $3$
2. $4$
3. $3$

Exercise $\PageIndex{6}$

Simplify:

1. $\sqrt[3]{1000}$
2. $\sqrt[4]{16}$
3. $\sqrt[5]{243}$

Answer

1. $10$
2. $2$
3. $3$

In this example be alert for the negative signs as well as even and odd powers.

Example $\PageIndex{4}$

Simplify:

1. $\sqrt[3]{-125}$
2. $\sqrt[4]{16}$
3. $\sqrt[5]{-243}$

Solution:

a.

$\sqrt[3]{-125}$

Since $(-5)^{3}=-125$.

$-5$

b.

$\sqrt[4]{16}$

Think, $(?)^{4}=-16$. No real number raised to the fourth power is negative.

Not a real number.

c.

$\sqrt[5]{-243}$

Since $(-3)^{5}=-243$.

$-3$

Exercise $\PageIndex{7}$

Simplify:

1. $\sqrt[3]{-27}$
2. $\sqrt[4]{-256}$
3. $\sqrt[5]{-32}$

Answer

1. $-3$
2. not real
3. $-2$

Exercise $\PageIndex{8}$

Simplify:

1. $\sqrt[3]{-216}$
2. $\sqrt[4]{-81}$
3. $\sqrt[5]{-1024}$

Answer

1. $-6$
2. not real
3. $-4$

Estimate and Approximate Roots

When we see a number with a radical sign, we often don’t think about its numerical value. While we probably know that the $\sqrt{4}=2$, what is the value of $\sqrt{21}$ or $\sqrt[3]{50}$? In some situations a quick estimate is meaningful and in others it is convenient to have a decimal approximation.

To get a numerical estimate of a square root, we look for perfect square numbers closest to the radicand. To find an estimate of $\sqrt{11}$, we see $11$ is between perfect square numbers $9$ and $16$, closer to $9$. Its square root then will be between $3$ and $4$, but closer to $3$.

Figure 8.1.4

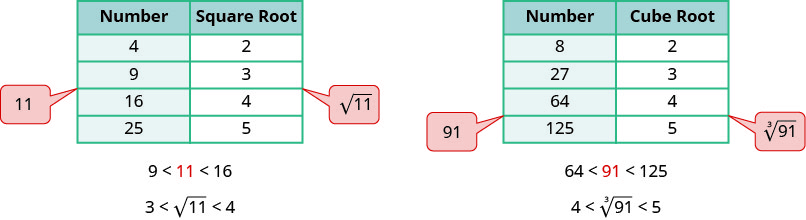
Similarly, to estimate $\sqrt[3]{91}$, we see $91$ is between perfect cube numbers $64$ and $125$. The cube root then will be between $4$ and $5$.

Example $\PageIndex{5}$

Estimate each root between two consecutive whole numbers:

1. $\sqrt{105}$
2. $\sqrt[3]{43}$

Solution:

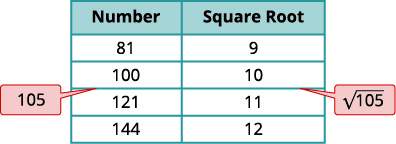
a. Think of the perfect square numbers closest to $105$. Make a small table of these perfect squares and their squares roots.

Table 8.1.1

	$\sqrt{105}$
Locate $105$ between two consecutive perfect squares.	$100<\color{red}105 \color{black} <121$
$\sqrt{105}$ is between their square roots.	$10< \color{red}\sqrt{105}< \color{black}11$

b. Similarly we locate $43$ between two perfect cube numbers.

Table 8.1.2

	$\sqrt[3]{43}$
Locate $43$ between two consecutive perfect cubes.
$\sqrt[3]{43}$ is between their cube roots.

Exercise $\PageIndex{9}$

Estimate each root between two consecutive whole numbers:

1. $\sqrt{38}$
2. $\sqrt[3]{93}$

Answer

1. $6<\sqrt{38}<7$
2. $4<\sqrt[3]{93}<5$

Exercise $\PageIndex{10}$

Estimate each root between two consecutive whole numbers:

1. $\sqrt{84}$
2. $\sqrt[3]{152}$

Answer

1. $9<\sqrt{84}<10$
2. $5<\sqrt[3]{152}<6$

There are mathematical methods to approximate square roots, but nowadays most people use a calculator to find square roots. To find a square root you will use the $\sqrt{x}$ key on your calculator. To find a cube root, or any root with higher index, you will use the $\sqrt[y]{x}$ key.

When you use these keys, you get an approximate value. It is an approximation, accurate to the number of digits shown on your calculator’s display. The symbol for an approximation is $≈$ and it is read ‘approximately’.

Suppose your calculator has a $10$ digit display. You would see that

$\sqrt{5} \approx 2.236067978$ rounded to two decimal places is $\sqrt{5} \approx 2.24$

$\sqrt[4]{93} \approx 3.105422799$ rounded to two decimal places is $\sqrt[4]{93} \approx 3.11$

How do we know these values are approximations and not the exact values? Look at what happens when we square them:

$\begin{aligned}(2.236067978)^{2} &=5.000000002 &(3.105422799)^{4}&=92.999999991 \\(2.24)^{2} &=5.0176 & (3.11)^{4}&=93.54951841 \end{aligned}$

Their squares are close to $5$, but are not exactly equal to $5$. The fourth powers are close to $93$, but not equal to $93$.

Example $\PageIndex{6}$

Round to two decimal places:

1. $\sqrt{17}$
2. $\sqrt[3]{49}$
3. $\sqrt[4]{51}$

Solution:

a.

$\sqrt{17}$

Use the calculator square root key.

$4.123105626 \dots$

Round to two decimal places.

$4.12$

$\sqrt{17} \approx 4.12$

b.

$\sqrt[3]{49}$

Use the calculator $\sqrt[y]{x}$ key.

$3.659305710 \ldots$

Round to two decimal places.

$3.66$

$\sqrt[3]{49} \approx 3.66$

c.

$\sqrt[4]{51}$

Use the calculator $\sqrt[y]{x}$ key.

$2.6723451177 \ldots$

Round to two decimal places.

$2.67$

$\sqrt[4]{51} \approx 2.67$

Exercise $\PageIndex{11}$

Round to two decimal places:

1. $\sqrt{11}$
2. $\sqrt[3]{71}$
3. $\sqrt[4]{127}$

Answer

1. $\approx 3.32$
2. $\approx 4.14$
3. $\approx 3.36$

Exercise $\PageIndex{12}$

Round to two decimal places:

1. $\sqrt{13}$
2. $\sqrt[3]{84}$
3. $\sqrt[4]{98}$

Answer

1. $\approx 3.61$
2. $\approx 4.38$
3. $\approx 3.15$

Simplify Variable Expressions with Roots

The odd root of a number can be either positive or negative. For example,

Figure 8.1.13

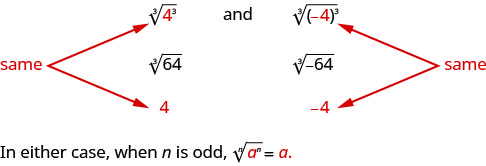
But what about an even root? We want the principal root, so $\sqrt[4]{625}=5$.

But notice,

Figure 8.1.14

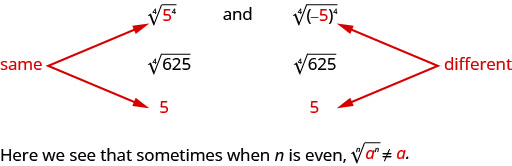
How can we make sure the fourth root of $−5$ raised to the fourth power is $5$? We can use the absolute value. $|−5|=5$. So we say that when $n$ is even $\sqrt[n]{a^{n}}=|a|$. This guarantees the principal root is positive.

Definition $\PageIndex{4}$: Simplifying Odd and Even Roots

For any integer $n\geq 2$,

when the index $n$ is odd $\sqrt[n]{a^{n}}=a$

when the index $n$ is even $\sqrt[n]{a^{n}}=|a|$

We must use the absolute value signs when we take an even root of an expression with a variable in the radical.

Example $\PageIndex{7}$

Simplify:

1. $\sqrt{x^{2}}$
2. $\sqrt[3]{n^{3}}$
3. $\sqrt[4]{p^{4}}$
4. $\sqrt[5]{y^{5}}$

Solution:

a. We use the absolute value to be sure to get the positive root.

$\sqrt{x^{2}}$

Since the index $n$ is even, $\sqrt[n]{a^{n}}=|a|$.

b. This is an odd indexed root so there is no need for an absolute value sign.

$\sqrt[3]{m^{3}}$

Since the index is $n$ is odd, $\sqrt[n]{a^{n}}=a$.

$m$

c.

$\sqrt[4]{p^{4}}$

Since the index $n$ is even $\sqrt[n]{a^{n}}=|a|$.

$|p|$

d.

$\sqrt[5]{y^{5}}$

Since the index $n$ is odd, $\sqrt[n]{a^{n}}=a$.

$y$

Exercise $\PageIndex{13}$

Simplify:

1. $\sqrt{b^{2}}$
2. $\sqrt[3]{w^{3}}$
3. $\sqrt[4]{m^{4}}$
4. $\sqrt[5]{q^{5}}$

Answer

1. $|b|$
2. $w$
3. $|m|$
4. $q$

Exercise $\PageIndex{14}$

Simplify:

1. $\sqrt{y^{2}}$
2. $\sqrt[3]{p^{3}}$
3. $\sqrt[4]{z^{4}}$
4. $\sqrt[5]{q^{5}}$

Answer

1. $|y|$
2. $p$
3. $|z|$
4. $q$

What about square roots of higher powers of variables? The Power Property of Exponents says $\left(a^{m}\right)^{n}=a^{m \cdot n}$. So if we square $a^{m}$, the exponent will become $2m$.

$\left(a^{m}\right)^{2}=a^{2 m}$

Looking now at the square root.

$\sqrt{a^{2 m}}$

Since $\left(a^{m}\right)^{2}=a^{2 m}$.

$\sqrt{\left(a^{m}\right)^{2}}$

Since $n$ is even $\sqrt[n]{a^{n}}=|a|$.

$\left|a^{m}\right|$

So $\sqrt{a^{2 m}}=\left|a^{m}\right|$.

We apply this concept in the next example.

Example $\PageIndex{8}$

Simplify:

1. $\sqrt{x^{6}}$
2. $\sqrt{y^{16}}$

Solution:

a.

$\sqrt{x^{6}}$

Since $\left(x^{3}\right)^{2}=x^{6}$.

$\sqrt{\left(x^{3}\right)^{2}}$

Since the index $n$ is even $\sqrt{a^{n}}=|a|$.

$\left|x^{3}\right|$

b.

$\sqrt{y^{16}}$

Since $\left(y^{8}\right)^{2}=y^{16}$.

$\sqrt{\left(y^{8}\right)^{2}}$

Since the index $n$ is even $\sqrt[n]{a^{n}}=|a|$.

$y^{8}$

In this case the absolute value sign is not needed as $y^{8}$ is positive.

Exercise $\PageIndex{15}$

Simplify:

1. $\sqrt{y^{18}}$
2. $\sqrt{z^{12}}$

Answer

1. $|y^{9}|$
2. $z^{6}$

Exercise $\PageIndex{16}$

Simplify:

1. $\sqrt{m^{4}}$
2. $\sqrt{b^{10}}$

Answer

1. $m^{2}$
2. $|b^{5}|$

The next example uses the same idea for higher roots.

Example $\PageIndex{9}$

Simplify:

1. $\sqrt[3]{y^{18}}$
2. $\sqrt[4]{z^{8}}$

Solution:

a.

$\sqrt[3]{y^{18}}$

Since $\left(y^{6}\right)^{3}=y^{18}$.

$\sqrt[3]{\left(y^{6}\right)^{3}}$

Since $n$ is odd, $\sqrt[n]{a^{n}}=a$.

$y^{6}$

b.

$\sqrt[4]{z^{8}}$

Since $\left(z^{2}\right)^{4}=z^{8}$.

$\sqrt[4]{\left(z^{2}\right)^{4}}$

Since $z^{2}$ is positive, we do not need an absolute value sign.

$z^{2}$

Exercise $\PageIndex{17}$

Simplify:

1. $\sqrt[4]{u^{12}}$
2. $\sqrt[3]{v^{15}}$

Answer

1. $|u^{3}|$
2. $v^{5}$

Exercise $\PageIndex{18}$

Simplify:

1. $\sqrt[5]{c^{20}}$
2. $\sqrt[6]{d^{24}}$

Answer

1. $c^{4}$
2. $d^{4}$

In the next example, we now have a coefficient in front of the variable. The concept $\sqrt{a^{2 m}}=\left|a^{m}\right|$ works in much the same way.

$\sqrt{16 r^{22}}=4\left|r^{11}\right|$ because $\left(4 r^{11}\right)^{2}=16 r^{22}$.

But notice $\sqrt{25 u^{8}}=5 u^{4}$ and no absolute value sign is needed as $u^{4}$ is always positive.

Example $\PageIndex{10}$

Simplify:

1. $\sqrt{16 n^{2}}$
2. $-\sqrt{81 c^{2}}$

Solution:

a.

$\sqrt{16 n^{2}}$

Since $(4 n)^{2}=16 n^{2}$.

$\sqrt{(4 n)^{2}}$

Since the index $n$ is even $\sqrt[n]{a^{n}}=|a|$.

$4|n|$

b.

$-\sqrt{81 c^{2}}$

Since $(9 c)^{2}=81 c^{2}$.

$-\sqrt{(9 c)^{2}}$

Since the index $n$ is even $\sqrt[n]{a^{n}}=|a|$.

$-9|c|$

Exercise $\PageIndex{19}$

Simplify:

1. $\sqrt{64 x^{2}}$
2. $-\sqrt{100 p^{2}}$

Answer

1. $8|x|$
2. $-10|p|$

Exercise $\PageIndex{20}$

Simplify:

1. $\sqrt{169 y^{2}}$
2. $-\sqrt{121 y^{2}}$

Answer

1. $13|y|$
2. $-11|y|$

This example just takes the idea farther as it has roots of higher index.

Example $\PageIndex{11}$

Simplify:

1. $\sqrt[3]{64 p^{6}}$
2. $\sqrt[4]{16 q^{12}}$

Solution:

a.

$\sqrt[3]{64 p^{6}}$

Rewrite $64p^{6}$ as $\left(4 p^{2}\right)^{3}$.

$\sqrt[3]{\left(4 p^{2}\right)^{3}}$

Take the cube root.

$4p^{2}$

b.

$\sqrt[4]{16 q^{12}}$

Rewrite the radicand as a fourth power.

$\sqrt[4]{\left(2 q^{3}\right)^{4}}$

Take the fourth root.

$2|q^{3}|$

Exercise $\PageIndex{21}$

Simplify:

1. $\sqrt[3]{27 x^{27}}$
2. $\sqrt[4]{81 q^{28}}$

Answer

1. $3x^{9}$
2. $3|q^{7}|$

Exercise $\PageIndex{22}$

Simplify:

1. $\sqrt[3]{125 q^{9}}$
2. $\sqrt[5]{243 q^{25}}$

Answer

1. $5p^{3}$
2. $3q^{5}$

The next examples have two variables.

Example $\PageIndex{12}$

Simplify:

1. $\sqrt{36 x^{2} y^{2}}$
2. $\sqrt{121 a^{6} b^{8}}$
3. $\sqrt[3]{64 p^{63} q^{9}}$

Solution:

a.

$\sqrt{36 x^{2} y^{2}}$

Since $(6 x y)^{2}=36 x^{2} y^{2}$

$\sqrt{(6 x y)^{2}}$

Take the square root.

$6|xy|$

b.

$\sqrt{121 a^{6} b^{8}}$

Since $\left(11 a^{3} b^{4}\right)^{2}=121 a^{6} b^{8}$

$\sqrt{\left(11 a^{3} b^{4}\right)^{2}}$

Take the square root.

$11\left|a^{3}\right| b^{4}$

c.

$\sqrt[3]{64 p^{63} q^{9}}$

Since $\left(4 p^{21} q^{3}\right)^{3}=64 p^{63} q^{9}$

$\sqrt[3]{\left(4 p^{21} q^{3}\right)^{3}}$

Take the cube root.

$4p^{21}q^{3}$

Exercise $\PageIndex{23}$

Simplify:

1. $\sqrt{100 a^{2} b^{2}}$
2. $\sqrt{144 p^{12} q^{20}}$
3. $\sqrt[3]{8 x^{30} y^{12}}$

Answer

1. $10|ab|$
2. $12p^{6}q^{10}$
3. $2x^{10}y^{4}$

Exercise $\PageIndex{24}$

Simplify:

1. $\sqrt{225 m^{2} n^{2}}$
2. $\sqrt{169 x^{10} y^{14}}$
3. $\sqrt[3]{27 w^{36} z^{15}}$

Answer

1. $15|mn|$
2. $13\left|x^{5} y^{7}\right|$
3. $3w^{12}z^{5}$

Access this online resource for additional instruction and practice with simplifying expressions with roots.

• Simplifying Variables Exponents with Roots using Absolute Values

Key Concepts

• Square Root Notation
  • $\sqrt{m}$ is read ‘the square root of $m$’
  • If $n^{2}=m$, then $n=\sqrt{m}$, for $n≥0$.
    
    Figure 8.1.1
  • The square root of $m$, $\sqrt{m}$, is a positive number whose square is $m$.
• n^th Root of a Number
  • If $b^{n}=a$, then $b$ is an $n^{th}$ root of $a$.
  • The principal $n^{th}$ root of $a$ is written $\sqrt[n]{a}$.
  • $n$ is called the index of the radical.
• Properties of $\sqrt[n]{a}$
  • When $n$ is an even number and
    • $a≥0$, then $\sqrt[n]{a}$ is a real number
    • $a<0$, then $\sqrt[n]{a}$ is not a real number
  • When $n$ is an odd number, $\sqrt[n]{a}$ is a real number for all values of $a$.
• Simplifying Odd and Even Roots
  • For any integer $n≥2$,
    • when $n$ is odd $\sqrt[n]{a^{n}}=a$
    • when $n$ is even $\sqrt[n]{a^{n}}=|a|$
  • We must use the absolute value signs when we take an even root of an expression with a variable in the radical.

Glossary

square of a number

If $n^{2}=m$, then $m$ is the square of $n$.

square root of a number

If $n^{2}=m$, then $n$ is a square root of $m$.