10.1: Use the Language of Algebra (Part 1)

Learning Objectives

• Use variables and algebraic symbols
• Identify expressions and equations
• Simplify expressions with exponents
• Simplify expressions using the order of operations

Be Prepared!

Before you get started, take this readiness quiz.

1. Add: $43 + 69$. If you missed this problem, review Example 1.2.8.
2. Multiply: $(896)201$. If you missed this problem, review Example 1.4.11.
3. Divide: $7,263 ÷ 9$. If you missed this problem, review Example 1.5.8.

Use Variables and Algebraic Symbols

Greg and Alex have the same birthday, but they were born in different years. This year Greg is $20$ years old and Alex is $23$, so Alex is $3$ years older than Greg. When Greg was $12$, Alex was $15$. When Greg is $35$, Alex will be $38$. No matter what Greg’s age is, Alex’s age will always be $3$ years more, right?

In the language of algebra, we say that Greg’s age and Alex’s age are variable and the three is a constant. The ages change, or vary, so age is a variable. The $3$ years between them always stays the same, so the age difference is the constant.

In algebra, letters of the alphabet are used to represent variables. Suppose we call Greg’s age $g$. Then we could use $g + 3$ to represent Alex’s age. See Table $\PageIndex{1}$.

Table $\PageIndex{1}$

Greg’s age	Alex’s age
12	15
20	23
35	38
g	g + 3

Letters are used to represent variables. Letters often used for variables are $x, y, a, b,$ and $c$.

Definition: Variables and Constants

A variable is a letter that represents a number or quantity whose value may change.

A constant is a number whose value always stays the same.

To write algebraically, we need some symbols as well as numbers and variables. There are several types of symbols we will be using. In Whole Numbers, we introduced the symbols for the four basic arithmetic operations: addition, subtraction, multiplication, and division. We will summarize them here, along with words we use for the operations and the result.

Table $\PageIndex{2}$

Operation	Notation	Say:	The result is...
Addition	a + b	a plus b	the sum of a and b
Subtraction	a − b	a minus b	the difference of a and b
Multiplication	a • b, (a)(b), (a)b, a(b)	a times b	the product of a and b
Division	a ÷ b, a / b, $\dfrac{a}{b}$, $b \overline{)a}$	a divided by b	the quotient of a and b

In algebra, the cross symbol, $×$, is not used to show multiplication because that symbol may cause confusion. Does $3xy$ mean $3 × y$ (three times $y$) or $3 • x • y$ (three times $x$ times $y$)? To make it clear, use $•$ or parentheses for multiplication.

We perform these operations on two numbers. When translating from symbolic form to words, or from words to symbolic form, pay attention to the words of or and to help you find the numbers.

The sum of $5$ and $3$ means add $5$ plus $3$, which we write as $5 + 3$.

The difference of $9$ and $2$ means subtract $9$ minus $2$, which we write as $9 − 2$.

The product of $4$ and $8$ means multiply $4$ times $8$, which we can write as $4 • 8$.

The quotient of $20$ and $5$ means divide $20$ by $5$, which we can write as $20 ÷ 5$.

Example $\PageIndex{1}$: translate to words

Translate from algebra to words:

1. $12 + 14$
2. $(30)(5)$
3. $64 ÷ 8$
4. $x − y$

Solution

12 + 14

12 plus 14

the sum of twelve and fourteen

(30)(5)

30 times 5

the product of thirty and five

64 ÷ 8

64 divided by 8

the quotient of sixty-four and eight

x − y

x minus y

the difference of x and y

exercise $\PageIndex{1}$

Translate from algebra to words.

1. $18 + 11$
2. $(27)(9)$
3. $84 ÷ 7$
4. $p − q$

Answer a

$18$ plus $11$; the sum of eighteen and eleven

Answer b

$27$ times $9$; the product of twenty-seven and nine

Answer c

$84$ divided by $7$; the quotient of eighty-four and seven

Answer d

$p$ minus $q$; the difference of $p$ and $q$

exercise $\PageIndex{2}$

Translate from algebra to words.

1. $47 − 19$
2. $72 ÷ 9$
3. $m + n$
4. $(13)(7)$

Answer a

$47$ minus $19$; the difference of forty-seven and nineteen

Answer b

$72$ divided by $9$; the quotient of seventy-two and nine

Answer c

$m$ plus $n$; the sum of $m$ and $n$

Answer d

$13$ times $7$; the product of thirteen and seven

When two quantities have the same value, we say they are equal and connect them with an equal sign.

Definition: Equality Symbol

$a = b$ is read $a$ is equal to $b$

The symbol $=$ is called the equal sign.

An inequality is used in algebra to compare two quantities that may have different values. The number line can help you understand inequalities. Remember that on the number line the numbers get larger as they go from left to right. So if we know that $b$ is greater than $a$, it means that $b$ is to the right of $a$ on the number line. We use the symbols "$<$" and "$>$" for inequalities.

Definition: Inequality

$a < b$ is read $a$ is less than $b$

$a$ is to the left of $b$ on the number line

$a > b$ is read $a$ is greater than $b$

$a$ is to the right of $b$ on the number line

The expressions $a < b$ and $a > b$ can be read from left-to-right or right-to-left, though in English we usually read from left-to-right. In general, $a < b$ is equivalent to $b > a$. For example, $7 < 11$ is equivalent to $11 > 7$. $a > b$ is equivalent to $b < a$. For example, $17 > 4$ is equivalent to $4 < 17$.

When we write an inequality symbol with a line under it, such as $a ≤ b$, it means $a < b$ or $a = b$. We read this $a$ is less than or equal to $b$. Also, if we put a slash through an equal sign, $≠$, it means not equal.

We summarize the symbols of equality and inequality in Table $\PageIndex{3}$.

Table $\PageIndex{3}$

Algebraic Notation	Say
a = b	a is equal to b
a ≠ b	a is not equal to b
a < b	a is less than b
a > b	a is greater than b
a ≤ b	a is less than or equal to b
a ≥ b	a is greater than or equal to b

Definition: Symbols $<$ and $>$

The symbols $<$ and $>$ each have a smaller side and a larger side.

smaller side $<$ larger side

larger side $>$ smaller side

The smaller side of the symbol faces the smaller number and the larger faces the larger number.

Example $\PageIndex{2}$: translate to words

Translate from algebra to words:

1. $20 ≤ 35$
2. $11 ≠ 15 − 3$
3. $9 > 10 ÷ 2$
4. $x + 2 < 10$

Solution

20 ≤ 35

20 is less than or equal to 35

11 ≠ 15 − 3

11 is not equal to 15 minus 3

9 > 10 ÷ 2

9 is greater than 10 divided by 2

x + 2 < 10

x plus 2 is less than 10

exercise $\PageIndex{3}$

Translate from algebra to words.

1. $14 ≤ 27$
2. $19 − 2 ≠ 8$
3. $12 > 4 ÷ 2$
4. $x − 7 < 1$

Answer a

fourteen is less than or equal to twenty-seven

Answer b

nineteen minus two is not equal to eight

Answer c

twelve is greater than four divided by two

Answer d

$x$ minus seven is less than one

exercise $\PageIndex{4}$

Translate from algebra to words.

1. $19 ≥ 15$
2. $7 = 12 − 5$
3. $15 ÷ 3 < 8$
4. $y - 3 > 6$

Answer a

nineteen is greater than or equal to fifteen

Answer b

seven is equal to twelve minus five

Answer c

fifteen divided by three is less than eight

Answer d

$y$ minus three is greater than six

Example $\PageIndex{3}$: translate

The information in Figure $\PageIndex{1}$ compares the fuel economy in miles-per-gallon (mpg) of several cars. Write the appropriate symbol =, in each expression to compare the fuel economy of the cars.

Figure $\PageIndex{1}$: (credit: modification of work by Bernard Goldbach, Wikimedia Commons)

1. MPG of Prius _____ MPG of Mini Cooper
2. MPG of Versa _____ MPG of Fit
3. MPG of Mini Cooper _____ MPG of Fit
4. MPG of Corolla _____ MPG of Versa
5. MPG of Corolla_____ MPG of Prius

Solution

	MPG of Prius____MPG of Mini Cooper
Find the values in the chart.	48____27
Compare.	48 > 27
	MPG of Prius > MPG of Mini Cooper

	MPG of Versa____MPG of Fit
Find the values in the chart.	26____27
Compare.	26 < 27
	MPG of Versa < MPG of Fit

	MPG of Mini Cooper____MPG of Fit
Find the values in the chart.	27____27
Compare.	27 = 27
	MPG of Mini Cooper = MPG of Fit

	MPG of Corolla____MPG of Versa
Find the values in the chart.	28____26
Compare.	28 > 26
	MPG of Corolla > MPG of Versa

	MPG of Corolla____MPG of Prius
Find the values in the chart.	28____48
Compare.	28 < 48
	MPG of Corolla < MPG of Prius

exercise $\PageIndex{5}$

Use Figure $\PageIndex{1}$ to fill in the appropriate symbol, $=$, $<$, or $>$.

1. MPG of Prius_____MPG of Versa
2. MPG of Mini Cooper_____ MPG of Corolla

Answer a

$>$

Answer b

$<$

exercise $\PageIndex{6}$

Use Figure $\PageIndex{1}$ to fill in the appropriate symbol, $=$, $<$, or $>$.

1. MPG of Fit_____ MPG of Prius
2. MPG of Corolla _____ MPG of Fit

Answer a

$<$

Answer b

$<$

Grouping symbols in algebra are much like the commas, colons, and other punctuation marks in written language. They indicate which expressions are to be kept together and separate from other expressions. Table $\PageIndex{4}$ lists three of the most commonly used grouping symbols in algebra.

Table $\PageIndex{4}$

Common Grouping Symbols
parentheses	( )
brackets	[ ]
braces	{ }

Here are some examples of expressions that include grouping symbols. We will simplify expressions like these later in this section.

$$8(14 - 8) \qquad 21 - 3[2 + 4(9 - 8)] \qquad 24 \div {13 - 2[1(6 - 5) + 4]} \nonumber$$

Identify Expressions and Equations

What is the difference in English between a phrase and a sentence? A phrase expresses a single thought that is incomplete by itself, but a sentence makes a complete statement. “Running very fast” is a phrase, but “The football player was running very fast” is a sentence. A sentence has a subject and a verb.

In algebra, we have expressions and equations. An expression is like a phrase. Here are some examples of expressions and how they relate to word phrases:

Table $\PageIndex{5}$

Expression	Words	Phrase
3 + 5	3 plus 5	the sum of three and five
n - 1	n minus one	the difference of n and one
6 • 7	6 times 7	the product of six and seven
$\dfrac{x}{y}$	x divided by y	the quotient of x and y

Notice that the phrases do not form a complete sentence because the phrase does not have a verb. An equation is two expressions linked with an equal sign. When you read the words the symbols represent in an equation, you have a complete sentence in English. The equal sign gives the verb. Here are some examples of equations:

Table $\PageIndex{6}$

Equation	Sentence
3 + 5 = 8	The sum of three and five is equal to eight.
n − 1 = 14	n minus one equals fourteen.
6 • 7 = 42	The product of six and seven is equal to forty-two.
x = 53	x is equal to fifty-three.
y + 9 = 2y − 3	y plus nine is equal to two y minus three.

Definition: Expressions and Equations

An expression is a number, a variable, or a combination of numbers and variables and operation symbols.

An equation is made up of two expressions connected by an equal sign.

Example $\PageIndex{4}$: expression or equation

Determine if each is an expression or an equation:

1. $16 − 6 = 10$
2. $4 • 2 + 1$
3. $x ÷ 25$
4. $y + 8 = 40$

Solution

(a) 16 − 6 = 10	This is an equation—two expressions are connected with an equal sign.
(b) 4 • 2 + 1	This is an expression—no equal sign.
(c) x ÷ 25	This is an expression—no equal sign.
(d) y + 8 = 40	This is an equation—two expressions are connected with an equal sign.

exercise $\PageIndex{7}$

Determine if each is an expression or an equation:

1. $23 + 6 = 29$
2. $7 • 3 − 7$

Answer a

equation

Answer b

expression

exercise $\PageIndex{8}$

Determine if each is an expression or an equation:

1. $y ÷ 14$
2. $x − 6 = 21$

Answer a

expression

Answer b

equation

Simplify Expressions with Exponents

To simplify a numerical expression means to do all the math possible. For example, to simplify $4 • 2 + 1$ we’d first multiply $4 • 2$ to get $8$ and then add the $1$ to get $9$. A good habit to develop is to work down the page, writing each step of the process below the previous step. The example just described would look like this:

$$\begin{split} 4 \cdot 2 + &1 \\ 8 + &1 \\ &9 \end{split}$$

Suppose we have the expression $2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2$. We could write this more compactly using exponential notation. Exponential notation is used in algebra to represent a quantity multiplied by itself several times. We write $2 • 2 • 2$ as $2^3$ and $2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2$ as $2^9$. In expressions such as $2^3$, the $2$ is called the base and the $3$ is called the exponent. The exponent tells us how many factors of the base we have to multiply.

means multiply three factors of $2$

We say $2^3$ is in exponential notation and $2 • 2 • 2$ is in expanded notation.

Definition: Exponential Notation

For any expression $a^n$, $a$ is a factor multiplied by itself $n$ times if $n$ is a positive integer.

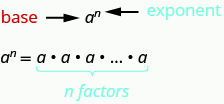
The expression $a^n$ is read $a$ to the $n^{th}$ power.

For powers of $n = 2$ and $n = 3$, we have special names. $a^2$ is read as "$a$ squared" $a^3$ is read as "$a$ cubed" Table $\PageIndex{7}$ lists some examples of expressions written in exponential notation.

Table $\PageIndex{7}$

Exponential Notation	In Words
$7^2$	7 to the second power, or 7 squared
$5^3$	5 to the third power, or 5 cubed
$9^4$	9 to the fourth power
$12^5$	12 to the fifth power

Example $\PageIndex{5}$: exponential form

Write each expression in exponential form:

1. $16 • 16 • 16 • 16 • 16 • 16 • 16$
2. $9 • 9 • 9 • 9 • 9$
3. $x • x • x • x$
4. $a • a • a • a • a • a • a • a$

Solution

(a) The base 16 is a factor 7 times.	$16^7$
(b) The base 9 is a factor 5 times.	$9^5$
(c) The base x is a factor 4 times.	$x^4$
(d) The base a is a factor 8 times.	$a^8$

exercise $\PageIndex{9}$

Write each expression in exponential form: $41 • 41 • 41 • 41 • 41$

Answer

$41^5$

exercise $\PageIndex{10}$

Write each expression in exponential form: $7 • 7 • 7 • 7 • 7 • 7 • 7 • 7 • 7$

Answer

$7^9$

Example $\PageIndex{6}$: expanded form

Write each exponential expression in expanded form:

1. $8^6$
2. $x^5$

Solution

1. The base is $8$ and the exponent is $6$, so $8^6$ means $8 • 8 • 8 • 8 • 8 • 8$
2. The base is $x$ and the exponent is $5$, so $x^5$ means $x • x • x • x • x$

exercise $\PageIndex{11}$

Write each exponential expression in expanded form:

1. $4^8$
2. $a^7$

Answer a

$4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4$

Answer b

$a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a$

exercise $\PageIndex{12}$

Write each exponential expression in expanded form:

1. $8^8$
2. $b^6$

Answer a

$8\cdot 8\cdot 8\cdot 8\cdot 8\cdot 8\cdot 8\cdot 8$

Answer b

$b\cdot b\cdot b\cdot b\cdot b\cdot b$

To simplify an exponential expression without using a calculator, we write it in expanded form and then multiply the factors.

Example $\PageIndex{7}$: simplify

Simplify: $3^4$.

Solution

Expand the expression.	3^4 = 3 • 3 • 3 • 3
Multiply left to right.	9 • 3 • 3 = 27 • 3
Multiply.	81

exercise $\PageIndex{13}$

Simplify:

1. $5^3$
2. $1^7$

Answer a

$125$

Answer b

$1$

exercise $\PageIndex{14}$

Simplify:

1. $7^2$
2. $0^5$

Answer a

$49$

Answer b

$0$

Contributors and Attributions

• Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.