Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

12.7E: Exercises for Cylindrical and Spherical Coordinates

  1. Last updated
  2. Save as PDF
  • Page ID
    20196

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

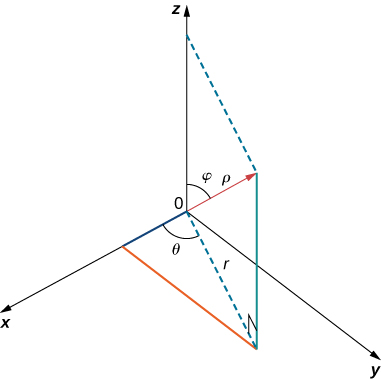
    Use the following figure as an aid in identifying the relationship between the rectangular, cylindrical, and spherical coordinate systems.

    For exercises 1 - 4, the cylindrical coordinates \( (r,θ,z)\) of a point are given. Find the rectangular coordinates \( (x,y,z)\) of the point.

    1) \( (4,\frac{π}{6},3)\)

    Answer:
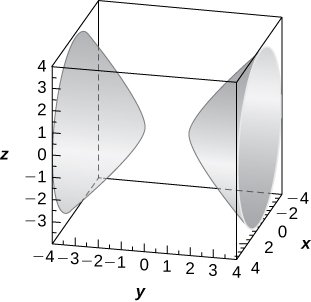
    \( (2\sqrt{3},2,3)\)

    2) \( (3,\frac{π}{3},5)\)

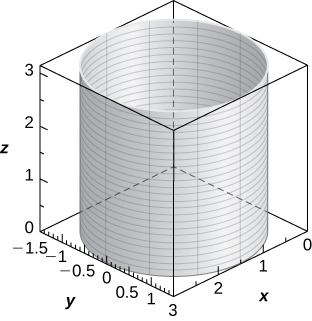
    3) \( (4,\frac{7π}{6},3)\)

    Answer:
    \( −2\sqrt{3},−2,3)\)

    4) \( (2,π,−4)\)

    For exercises 5 - 8, the rectangular coordinates \( (x,y,z)\) of a point are given. Find the cylindrical coordinates \( (r,θ,z)\)of the point.

    5) \( (1,\sqrt{3},2)\)

    Answer:
    \( (2,\frac{π}{3},2)\)

    6) \( (1,1,5)\)

    7) \( (3,−3,7)\)

    Answer:
    \( (3\sqrt{2},−\frac{π}{4},7)\)

    8) \( (−2\sqrt{2},2\sqrt{2},4)\)

    For exercises 9 - 16, the equation of a surface in cylindrical coordinates is given. Find the equation of the surface in rectangular coordinates. Identify and graph the surface.

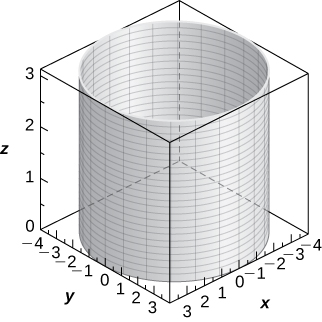
    9) [T] \( r=4\)

    Answer:

    A cylinder of equation \( x^2+y^2=16,\) with its center at the origin and rulings parallel to the \(z\)-axis,

    10) [T] \( z=r^2cos^2θ\)

    11) [T] \( r^2cos(2θ)+z^2+1=0\)

    Answer:

    Hyperboloid of two sheets of equation \( −x^2+y^2−z^2=1,\) with the y-axis as the axis of symmetry,

    12) [T] \( r=3sinθ\)

    13) [T] \( r=2cosθ\)

    Answer:

    Cylinder of equation \( x^2−2x+y^2=0,\) with a center at \( (1,0,0)\) and radius \( 1\), with rulings parallel to the z-axis,

    14) [T] \( r^2+z^2=5\)

    15) [T] \( r=2secθ\)

    Answer:

    Plane of equation \( x=2,\)

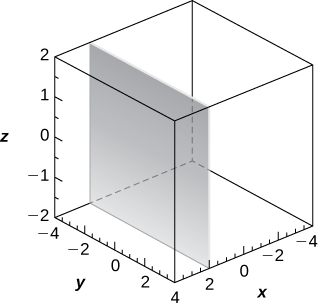
    16) [T] \( r=3cscθ\)

    For exercises 17 - 22, the equation of a surface in rectangular coordinates is given. Find the equation of the surface in cylindrical coordinates.

    17) \( z=3\)

    Answer:
    \( z=3\)

    18) \( x=6\)

    19) \( x^2+y^2+z^2=9\)

    Answer:
    \( r^2+z^2=9\)

    20) \( y=2x^2\)

    21) \( x^2+y^2−16x=0\)

    Answer:
    \( r=16\cos θ,r=0\)

    22) \( x^2+y^2−3\sqrt{x^2+y^2}+2=0\)

    For exercises 23 - 26, the spherical coordinates \( (ρ,θ,φ)\) of a point are given. Find the rectangular coordinates \( (x,y,z)\) of the point.

    23) \( (3,0,π)\)

    Answer:
    \( (0,0,−3)\)

    24) \( (1,\frac{π}{6},\frac{π}{6})\)

    25) \( (12,−\frac{π}{4},\frac{π}{4})\)

    Answer:
    \( (6,−6,\sqrt{2})\)

    26) \( (3,\frac{π}{4},\frac{π}{6})\)

    For exercises 27 - 30, the rectangular coordinates \( (x,y,z)\) of a point are given. Find the spherical coordinates \( (ρ,θ,φ)\) of the point. Express the measure of the angles in degrees rounded to the nearest integer.

    27) \( (4,0,0)\)

    Answer:
    \( (4,0,90°)\)

    28) \( (−1,2,1)\)

    29) \( (0,3,0)\)

    Answer:
    \( (3,90°,90°)\)

    30) \( (−2,2\sqrt{3},4)\)

    For exercises 31 - 36, the equation of a surface in spherical coordinates is given. Find the equation of the surface in rectangular coordinates. Identify and graph the surface.

    31) [T] \( ρ=3\)

    Answer:

    Sphere of equation \( x^2+y^2+z^2=9\) centered at the origin with radius \( 3\),

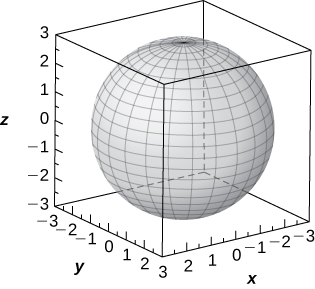
    32) [T] \( φ=\frac{π}{3}\)

    33) [T] \( ρ=2cosφ\)

    Answer:

    Sphere of equation \( x^2+y^2+(z−1)^2=1\) centered at \( (0,0,1)\) with radius \( 1\),

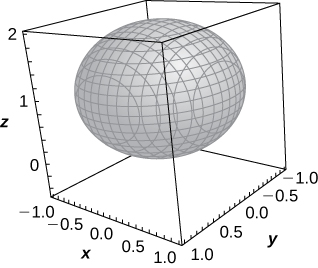
    34) [T] \( ρ=4cscφ\)

    35) [T] \( φ=\frac{π}{2}\)

    Answer:

    The \(xy\)-plane of equation \( z=0,\)

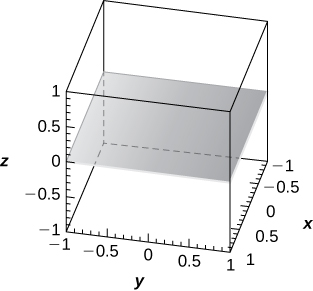
    36) [T] \( ρ=6cscφsecθ\)

    For exercises 37 - 40, the equation of a surface in rectangular coordinates is given. Find the equation of the surface in spherical coordinates. Identify the surface.

    37) \( x^2+y^2−3z^2=0, z≠0\)

    Answer:
    \( φ=\frac{π}{3}\) or \( φ=\frac{2π}{3};\) Elliptic cone

    38) \( x^2+y^2+z^2−4z=0\)

    39) \( z=6\)

    Answer:
    \( ρcosφ=6;\) Plane at \( z=6\)

    40) \( x^2+y^2=9\)

    For exercises 41 - 44, the cylindrical coordinates of a point are given. Find its associated spherical coordinates, with the measure of the angle φ in radians rounded to four decimal places.

    41) [T] \( (1,\frac{π}{4},3)\)

    Answer:
    \( (\sqrt{10},\frac{π}{4},0.3218)\)

    42) [T] \( (5,π,12)\)

    43) \( (3,\frac{π}{2},3)\)

    Answer:
    \( (3\sqrt{2},\frac{π}{2},\frac{π}{4})\)

    44) \( (3,−\frac{π}{6},3)\)

    For exercises 45 - 48, the spherical coordinates of a point are given. Find its associated cylindrical coordinates.

    45) \( (2,−\frac{π}{4},\frac{π}{2})\)

    Answer:
    \( (2,−\frac{π}{4},0)\)

    46) \( (4,\frac{π}{4},\frac{π}{6})\)

    47) \( (8,\frac{π}{3},\frac{π}{2})\)

    Answer:
    \( (8,\frac{π}{3},0)\)

    48) \( (9,−\frac{π}{6},\frac{π}{3})\)

    For exercises 49 - 52, find the most suitable system of coordinates to describe the solids.

    49) The solid situated in the first octant with a vertex at the origin and enclosed by a cube of edge length \( a\), where \( a>0\)

    Answer:
    Cartesian system, \( {(x,y,z)|0≤x≤a,0≤y≤a,0≤z≤a}\)

    50) A spherical shell determined by the region between two concentric spheres centered at the origin, of radii of \( a\) and \( b\), respectively, where \( b>a>0\)

    51) A solid inside sphere \( x^2+y^2+z^2=9\) and outside cylinder \( (x−\frac{3}{2})^2+y^2=\frac{9}{4}\)

    Answer:
    Cylindrical system, \( {(r,θ,z)∣r^2+z^2≤9,r≥3cosθ,0≤θ≤2π}\)

    52) A cylindrical shell of height \( 10\) determined by the region between two cylinders with the same center, parallel rulings, and radii of \( 2\) and \( 5\), respectively

    53) [T] Use a CAS or CalcPlot3D to graph in cylindrical coordinates the region between elliptic paraboloid \( z=x^2+y^2\) and cone \( x^2+y^2−z^2=0.\)

    Answer:

    The region is described by the set of points \( {(r,θ,z)∣∣0≤r≤1,0≤θ≤2π,r^2≤z≤r}.\)

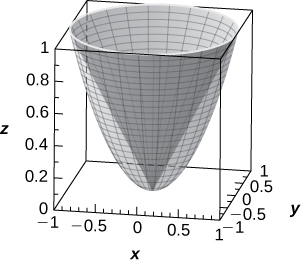
    54) [T] Use a CAS or CalcPlot3D to graph in spherical coordinates the “ice cream-cone region” situated above the xy-plane between sphere \( x^2+y^2+z^2=4\) and elliptical cone \( x^2+y^2−z^2=0.\)

    55) Washington, DC, is located at \( 39°\) N and \( 77°\) W (see the following figure). Assume the radius of Earth is \( 4000\) mi. Express the location of Washington, DC, in spherical coordinates.

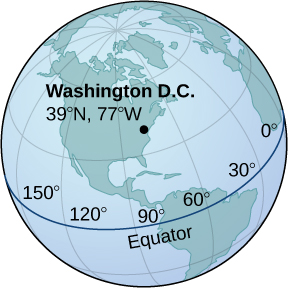
    Answer:
    \( (4000,−77°,51°)\)

    56) San Francisco is located at \( 37.78°N\) and \( 122.42°W.\) Assume the radius of Earth is \( 4000\)mi. Express the location of San Francisco in spherical coordinates.

    57) Find the latitude and longitude of Rio de Janeiro if its spherical coordinates are \( (4000,−43.17°,102.91°).\)

    Answer:
    \( 43.17°W, 22.91°S\)

    58) Find the latitude and longitude of Berlin if its spherical coordinates are \( (4000,13.38°,37.48°).\)

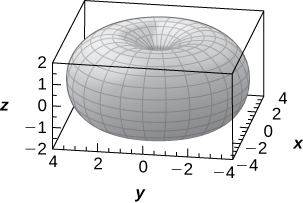
    59) [T] Consider the torus of equation \( (x^2+y^2+z^2+R^2−r^2)^2=4R^2(x^2+y^2),\) where \( R≥r>0.\)

    a. Write the equation of the torus in spherical coordinates.

    b. If \( R=r,\) the surface is called a horn torus. Show that the equation of a horn torus in spherical coordinates is \( ρ=2Rsinφ.\)

    c. Use a CAS or CalcPlot3D to graph the horn torus with \( R=r=2\) in spherical coordinates.

    Answer:

    a. \(ρ=0, ρ+R2−r2−2Rsinφ=0\)

    c.

    60) [T] The “bumpy sphere” with an equation in spherical coordinates is \( ρ=a+bcos(mθ)sin(nφ)\), with \( θ∈[0,2π]\) and \( φ∈[0,π]\), where \( a\) and \( b\) are positive numbers and \( m\) and \( n\) are positive integers, may be used in applied mathematics to model tumor growth.

    a. Show that the “bumpy sphere” is contained inside a sphere of equation \( ρ=a+b.\) Find the values of \( θ\) and \( φ\) at which the two surfaces intersect.

    b. Use a CAS or CalcPlot3D to graph the surface for \( a=14, b=2, m=4,\) and \( n=6\) along with sphere \( ρ=a+b.\)

    c. Find the equation of the intersection curve of the surface at b. with the cone \( φ=\frac{π}{12}\). Graph the intersection curve in the plane of intersection.

    Contributors

    Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

    Exercises and LaTeX edited by Paul Seeburger