Exercises for Limits and Continuity

Last updated
Save as PDF

Page ID: 21120

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

1) Use the limit laws for functions of two variables to evaluate each limit below, given that $\displaystyle \lim_{(x,y)→(a,b)}f(x,y) = 5$ and $\displaystyle \lim_{(x,y)→(a,b)}g(x,y) = 2$.

$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) + g(x,y)\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) g(x,y)\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[ \dfrac{7f(x,y)}{g(x,y)}\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[\dfrac{2f(x,y) - 4g(x,y)}{f(x,y) - g(x,y)}\right]$

Answer:

$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) + g(x,y)\right] = \displaystyle \lim_{(x,y)→(a,b)}f(x,y) + \displaystyle \lim_{(x,y)→(a,b)}g(x,y)= 5 + 2 = 7$
$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) g(x,y)\right] =\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right) \left(\displaystyle \lim_{(x,y)→(a,b)}g(x,y)\right) = 5(2) = 10$
$\displaystyle \lim_{(x,y)→(a,b)}\left[ \dfrac{7f(x,y)}{g(x,y)}\right] = \frac{7\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right)}{\displaystyle \lim_{(x,y)→(a,b)}g(x,y)}=\frac{7(5)}{2} = 17.5$
$\displaystyle \lim_{(x,y)→(a,b)}\left[\dfrac{2f(x,y) - 4g(x,y)}{f(x,y) - g(x,y)}\right] = \frac{2\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right) - 4 \left(\displaystyle \lim_{(x,y)→(a,b)}g(x,y)\right)}{\displaystyle \lim_{(x,y)→(a,b)}f(x,y) - \displaystyle \lim_{(x,y)→(a,b)}g(x,y)}= \frac{2(5) - 4(2)}{5 - 2} = \frac{2}{3}$

In exercises 2 - 4, find the limit of the function.

2) $\displaystyle \lim_{(x,y)→(1,2)}x$

3) $\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2}$

Answer:: $\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2} = 2$

4) Show that the limit $\displaystyle \lim_{(x,y)→(0,0)}\frac{5x^2y}{x^2+y^2}$ exists and is the same along the paths: $y$-axis and $x$-axis, and along $ y=x$.

In exercises 5 - 19, evaluate the limits at the indicated values of $x$ and $y$. If the limit does not exist, state this and explain why the limit does not exist.

5) $\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6}$

Answer:: $\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6} = \frac{2}{3} $

6) $\displaystyle \lim_{(x,y)→(11,13)}\sqrt{\frac{1}{xy}}$

7) $\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2\sin x}{x}$

Answer:: $\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2\sin x}{x} = 1$

8) $\displaystyle \lim_{(x,y)→(0,0)}\sin(\frac{x^8+y^7}{x−y+10})$

9) $\displaystyle \lim_{(x,y)→(π/4,1)}\frac{y\tan x}{y+1}$

Answer:: $\displaystyle \lim_{(x,y)→(π/4,1)}\frac{y\tan x}{y+1}=\frac{1}{2}$

10) $\displaystyle \lim_{(x,y)→(0,π/4)}\frac{\sec x+2}{3x−\tan y}$

11) $\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y})$

Answer:: $\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y}) = −\frac{1}{2}$

12) $\displaystyle \lim_{(x,y)→(4,4)}x\ln y$

13) $\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2}$

Answer:: $\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2} = e^{−32}$

14) $\displaystyle \lim_{(x,y)→(0,0)}\sqrt{9−x^2−y^2}$

15) $\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y)$

Answer:: $\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y) = 11$

16) $\displaystyle \lim_{(x,y)→(π,π)}x\sin(\frac{x+y}{4})$

17) $\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1}$

Answer:: $\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1} = 1$

18) $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2+y^2}{\sqrt{x^2+y^2+1}−1}$

19) $\displaystyle \lim_{(x,y)→(0,0)}\ln(x^2+y^2)$

Answer:: The limit does not exist because when $x$ and $y$ both approach zero, the function approaches $ \ln 0$, which is undefined (approaches negative infinity).

In exercises 20 - 21, complete the statement.

20) A point $ (x_0,y_0)$ in a plane region $ R$ is an interior point of $R$ if _________________.

21) A point $ (x_0,y_0)$ in a plane region $R$ is called a boundary point of $R$ if ___________.

Answer:: Every open disk centered at $ (x_0,y_0)$ contains points inside $ R$ and outside $ R$.

In exercises 22 - 25, use algebraic techniques to evaluate the limit.

22) $\displaystyle \lim_{(x,y)→(2,1)}\frac{x−y−1}{\sqrt{x−y}−1}$

23) $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2}$

Answer:: $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2} = 0$

24) $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^3−y^3}{x−y}$

25) $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}}$

Answer:: $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}} = 0$

In exercises 26 - 27, evaluate the limits of the functions of three variables.

26) $\displaystyle \lim_{(x,y,z)→(1,2,3)}\frac{xz^2−y^2z}{xyz−1}$

27) $\displaystyle \lim_{(x,y,z)→(0,0,0)}\frac{x^2−y^2−z^2}{x^2+y^2−z^2}$

Answer:: The limit does not exist.

In exercises 28 - 31, evaluate the limit of the function by determining the value the function approaches along the indicated paths. If the limit does not exist, explain why not.

28) $\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$

a. Along the $x$-axis $ (y=0)$

b. Along the $y$-axis $ (x=0)$

c. Along the path $y=2x$

29) Evaluate $\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$ using the results of previous problem.

Answer:: The limit does not exist. The function approaches two different values along different paths.

30) $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$

a. Along the $x$-axis $ (y=0)$

b. Along the $y$-axis $ (x=0)$

c. Along the path $y=x^2$

31) Evaluate $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$ using the results of previous problem.

Answer:: The limit does not exist because the function approaches two different values along the paths.

In exercises 32 - 35, discuss the continuity of each function. Find the largest region in the $xy$-plane in which each function is continuous.

32) $ f(x,y)=\sin(xy)$

33) $ f(x,y)=\ln(x+y)$

Answer:: The function $ f$ is continuous in the region $ y>−x.$

34) $ f(x,y)=e^{3xy}$

35) $ f(x,y)=\dfrac{1}{xy}$

Answer:: The function $f$ is continuous at all points in the $xy$-plane except at points on the $x$- and $y$-axes.

In exercises 36 - 38, determine the region in which the function is continuous. Explain your answer.

36) $ f(x,y)=\dfrac{x^2y}{x^2+y^2}$

37) $ f(x,y)=$$ \begin{cases}\dfrac{x^2y}{x^2+y^2} & if(x,y)≠(0,0)\\0 & if(x,y)=(0,0)\end{cases}$

Hint:: Show that the function approaches different values along two different paths.

Answer:: The function is continuous at $ (0,0)$ since the limit of the function at $ (0,0)$ is $ 0$, the same value of $ f(0,0).$

38) $ f(x,y)=\dfrac{\sin(x^2+y^2)}{x^2+y^2}$

39) Determine whether $ g(x,y)=\dfrac{x^2−y^2}{x^2+y^2}$ is continuous at $ (0,0)$.

Answer:: The function is discontinuous at $ (0,0).$ The limit at $ (0,0)$ fails to exist and $ g(0,0)$ does not exist.

40) Create a plot using graphing software to determine where the limit does not exist. Determine the region of the coordinate plane in which $ f(x,y)=\dfrac{1}{x^2−y}$ is continuous.

41) Determine the region of the $xy$-plane in which the composite function $ g(x,y)=\arctan(\frac{xy^2}{x+y})$ is continuous. Use technology to support your conclusion.

Answer:: Since the function $ \arctan x$ is continuous over $ (−∞,∞), g(x,y)=\arctan(\frac{xy^2}{x+y})$ is continuous where $ z=\dfrac{xy^2}{x+y}$ is continuous. The inner function $ z$ is continuous on all points of the $xy$-plane except where $ y=−x.$ Thus, $ g(x,y)=\arctan(\frac{xy^2}{x+y})$ is continuous on all points of the coordinate plane except at points at which $ y=−x.$

42) Determine the region of the $xy$-plane in which $ f(x,y)=\ln(x^2+y^2−1)$ is continuous. Use technology to support your conclusion. (Hint: Choose the range of values for $ x$ and $ y$ carefully!)

43) At what points in space is $ g(x,y,z)=x^2+y^2−2z^2$ continuous?

Answer:: All points $ P(x,y,z)$ in space

44) At what points in space is $ g(x,y,z)=\dfrac{1}{x^2+z^2−1}$ continuous?

45) Show that $\displaystyle \lim_{(x,y)→(0,0)}\frac{1}{x^2+y^2}$ does not exist at $ (0,0)$ by plotting the graph of the function.

Answer:

The graph increases without bound as $ x$ and $ y$ both approach zero.

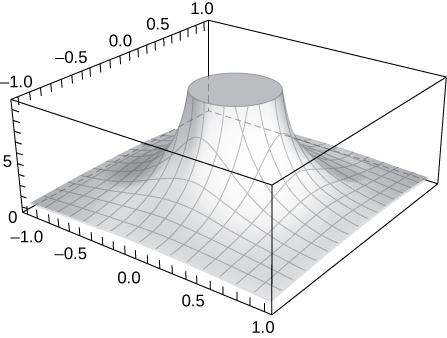
$The graph of a surface where the z-coordinate increases without bound as the input point (x, y) approaches the origin.$

46) [T] Evaluate $\displaystyle \lim_{(x,y)→(0,0)}\frac{−xy^2}{x^2+y^4}$ by plotting the function using a CAS. Determine analytically the limit along the path $ x=y^2.$

47) [T]

a. Use a CAS to draw a contour map of $ z=\sqrt{9−x^2−y^2}$.

b. What is the name of the geometric shape of the level curves?

c. Give the general equation of the level curves.

d. What is the maximum value of $ z$?

e. What is the domain of the function?

f. What is the range of the function?

Answer:

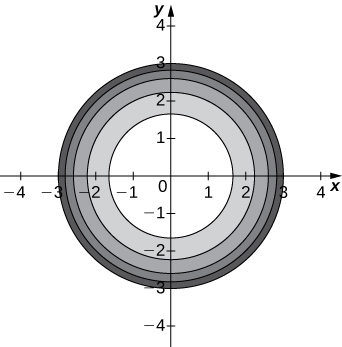
$Contour map of the function z=sqrt{9−x^2−y^2}$

b. The level curves are circles centered at $ (0,0)$ with radius $ 9−c$.
c. $ x^2+y^2=9−c$
d. $ z=3$
e. $ \{(x,y)∈R^2∣x^2+y^2≤9\}$
f. $ \{z|0≤z≤3\}$

48) True or False: If we evaluate $\displaystyle \lim_{(x,y)→(0,0)}f(x)$ along several paths and each time the limit is $ 1$, we can conclude that $\displaystyle \lim_{(x,y)→(0,0)}f(x)=1.$

49) Use polar coordinates to find $\displaystyle \lim_{(x,y)→(0,0)}\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}.$ You can also find the limit using L’Hôpital’s rule.

Answer:: $\displaystyle \lim_{(x,y)→(0,0)}\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}} = 1$

50) Use polar coordinates to find $\displaystyle \lim_{(x,y)→(0,0)}\cos(x^2+y^2).$

51) Discuss the continuity of $ f(g(x,y))$ where $ f(t)=1/t$ and $ g(x,y)=2x−5y.$

Answer:: $ f(g(x,y))$ is continuous at all points $ (x,y)$ that are not on the line $ 2x−5y=0.$

52) Given $ f(x,y)=x^2−4y,$ find $\displaystyle \lim_{h→0}\frac{f(x+h,y)−f(x,y)}{h}.$

53) Given $ f(x,y)=x^2−4y,$ find $\displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h}$.

Answer:: $ \displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h} = 2$

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Paul Seeburger (Monroe Community College) created problem 1.