1.1: Division Algorithm
- Page ID
- 131030
This page is a draft and is under active development.
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the proof of numerous theorems, we will utilize the well-ordering principle.
Every non-empty subset of \(\mathbb{N}\) has the smallest number.
Division Algorithm
Let \(a\) and \(b \ne 0\) be integers. Then there exist unique integers \(q\) and \(r\) such that \(a=bq+r, 0\leq r <|b|\), where \(q\) is the quotient and \(r\) is the remainder, and the absolute value of \(d\) is defined as:
\[|b|= \left\{ \begin{array}{c}
b, \mbox{if } b \geq 0\\
\\
-b, \mbox{if } b<0.
\end{array}
\right.\]
- Proof
-
We will show that \(q,r \in \mathbb{Z}\) exist and are unique.
Let \(a,b \in \mathbb{Z}\) s.t. \(b>0\).
Let \(S\) be a set defined by \(S=\{a-bm: a-bm \ge 0, m\in \mathbb{Z}\}\).
We will show existence by examining the possible cases.
Case 1: \( 0 \in S\)
If \(0 \in S\), then \(a-bm=0\) for some \(m \in \mathbb{Z}\).
Thus, \(a=bm\)
Since \(b|a\), \(q=m\) and \(r=0\).
Therefore existence has been proved.
Case 2: \(0 \notin S\).
Since \(0 \notin S\), we will show that \(S \ne \emptyset\) by examining the possible cases. Note: \(S \subseteq \mathbb{N}\).
Case a: \(a>0\).
Since \(a>0\), \(a=a-b(0)>0\).
Therefore \(a \in S\).
Case b: \(a<0\).
Consider \(a-bm\), where \(m=2a\).
Thus \(a-b(2a)=a(1-2b)\).
Consider \(1-2b\) is always negative since \(b>0, b \in \mathbb{N}\), thus greatest \(1-2b\) can be in \(-1\).
Therefore \(a(1-2b) \ge 0\) since \(b \ge 1\).
Note: The \(\ge\) could be > without loss of generality.
Since both case a & b are non-empty sets, \(S \ne \emptyset \subseteq \mathbb{N}\).
Thus \(S\) has the smallest element by the well-ordering principle, and lets call it \(r\).
That means \(r=a-bm\), for some \(m\in \mathbb{Z}\) where \(r \ge 0\).
Thus the non-empty set is \(r=a-bm \ge 0\).
We shall show that \(r < b\) by proceeding with a proof by contradiction.
Assume that \(r \ge b\).
Then \( a-b(m+1)=a-bm-b=r-b \ge 0\) for some \(m \in \mathbb{Z}\).
Then \(r-b \in S\) and \(r-b<r\). Note \((b>0)\)
This contradicts that \(r\) is the smallest element of \(S\).
Therefore \(r < b\).
Having examined all possible cases, \(a=bq+r, 0 \le r < b\) exists.
Next, we will show uniqueness.
Let \(r_1,r_2, q_1,q_2\) s.t. \(a=bq_1+r_1\) and \(a=bq_2+r_2\) with \( 0 \le r_1,r_2 < b\).
Consider \(bq_1+r_1=bq_2+r_2\), \(0 \le r_1<b\).
Further since \(b(q_1-q_2)=r_2-r_1\), \(b|(r_2-r_1)\), but \(b\) has to be \(\le r_1\).
Since, \(r_2-r_1 < b\), \(r_2-r_1=0\) and \(r_1=r_2\).
Hence \(q_1=q_2\).
Therefore uniqueness has been shown.
Example \(\PageIndex{1}\)
Find the \(q\) is the quotient and \(r\) is the remainder for the following values of \(n\) and \(d\).
- \(n=2018\) and \(d=343\).
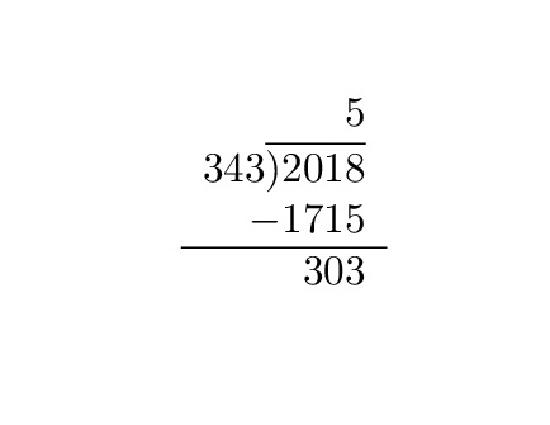
Thus \(2018=(5)(343)+303\).
2. \(n=-2018\) and \(d=343\).
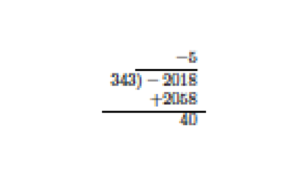
Thus \(-2018=(-6)(343)+40\).
3, . \(n=2018\) and \(d=-343\).
Thus \(2018=(6)(-343)+40\).
4.
\(n=-2018\) and \(d=-343\).
Thus \(-2018=(6)(-343)+ 40\).