1.3: Primes

Definition:

Prime Numbers - integers greater than $1$ with exactly $2$ positive divisors: $1$ and itself.
Let $n$ be a positive integer greater than $1$. Then $n$ is called a prime number if $n$ has exactly two positive divisors, $1$ and $n.$

Composite Numbers - integers greater than 1 which are not prime.

Note that: $1$ is neither prime nor composite.  

There are infinitely many primes, which was proved by Euclid in 100BC.

 

Example $\PageIndex{1}$: Method of Sieve of Eratosthenes

Examples of prime numbers are $2$ (this is the only even prime number), $3, 5, 7, 9, 11, 13, 17, \ldots$.

Method of Sieve of Eratosthenes:

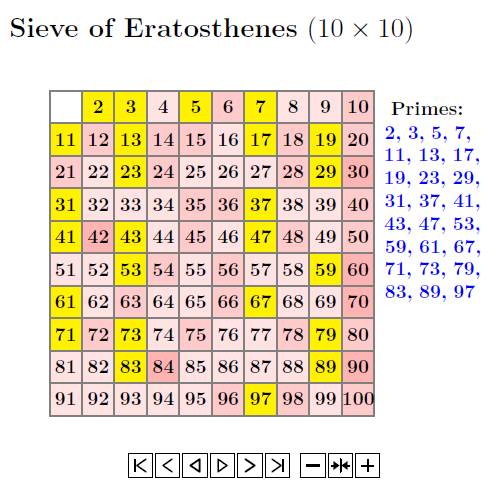
The following will provide us a way to decide given number is prime. 

Theorem $\PageIndex{1}$

Let $n$ be a composite number with exactly $3$ positive divisors. Then there exists a prime $p$ such that $n=p^2.$

Proof

Let $n$ be a positive integer with exactly $3$ positive divisors. Then two of the positive divisors are $1$ and $n.$
Let $d$ be the third positive divisor. Then $1 < d < n$ and the only positive divisors of $d$ are $1$ and $d.$
Therefore $d$ is prime.
Since $d \mid n$, $n=md, m \in\mathbb{Z_+}$.
Since $m \mid n$ and $1 <m<n, m=d, n=d^2.$
Thus, $d$ is prime. $\Box$

Theorem $\PageIndex{2}$

Every composite number $n$ has a prime divisor less than or equal to $\sqrt{n}$. If $p$ is a prime number and $p \mid n$, then $1<p \leq \sqrt{n}.$

Proof

Suppose $p$ be the smallest prime divisor of $n$. Then there exists an integer $m$ such that $n=pm$. Assume that $p > \sqrt{n}$. Then $m < \sqrt{n}.$

Let $q$ be any prime divisor of $m$. Then $q$ is also a prime divisor of $n$ and $q < m < \sqrt{n} < p.$ This is a contradiction.

 

Example $\PageIndex{2}$:

Is $223$ a prime number?

Solution:

The prime numbers $< \sqrt{223}$ are as follows: $2, 3, 5, 7, 11,$ and $13$. Note that $17^2 >223.$

Since $223$ is not divisible by any of the prime numbers identified above, $223$ is a prime number.

Exercise $\PageIndex{3}$

Is $2011$ a prime number?.

Answer

yes.

Theorem $\PageIndex{3}$: Prime divisibility theorem

Let $p$ be a prime number. If $p \mid ab, a,b \in \mathbb{Z},$ then $p\mid a$ or $p\mid b$.

Proof

Let $p$ be a prime number and let $a,b \in \mathbb{Z}.$  Assume that $p \mid ab$. If $p\mid a$, we are done. So we suppose that $p$ does not divide $a$. Thus $gcd(a,p)=1.$ Thus there exists $x,y \in \mathbb{Z}$ such that $1=ax+py$. Hence $b=abx+pby$. Since $p \mid ab$, $ab=pm, m\in \mathbb{Z}.$ Thus $b=pmx+pby=p(mx+by).$ Hence, $p\mid b.$

 

Theorem $\PageIndex{5}$

There are infinitely many primes.

Proof

Proof by contradiction.

Suppose there are finitely many primes $p_1, p_2, ...,p_n$, where $n$ is a positive integer. Consider the integer $Q$ such that

$$Q=p_1p_2...p_n+1.$$

Notice that $Q$ is not prime. Hence $Q$ has at least a prime divisor, say $q$. If we prove that $q$ is not one of the primes listed then we obtain a contradiction. Suppose now that $q=p_i$ for $1\leq i\leq n$. Thus $q$ divides $p_1p_2...p_n$ and as a result $q$ divides $Q-p_1p_2...p_n$. Therefore $q$ divides 1. But this is impossible since there is no prime that divides 1 and as a result $q$ is not one of the primes listed.

The following theorem explains the gaps between prime numbers:

Theorem $\PageIndex{5}$

Let $n$ be an integer. Then there exists $n$ consecutive composite integers.

Proof

Let $n$ be an integer. Consider the sequence of integers $$(n+1)!+2, (n+1)!+3,...,(n+1)!+n, (n+1)!+(n+1)$$

Notice that every integer in the above sequence is composite because $k$ divides $(n+1)!+k$ if $2\leq k\leq (n+1)$.

Example $\PageIndex{4}$:

Does there exist a block of $1000000$ consecutive integers without a prime number among them?

Solution

Use $1000001 !$ and consider $1000001 ! +2 , \ldots, 1000001!+1000001$

Example $\PageIndex{5}$:

Consider the formula $y=x^2+x+13$. Then

1. Find the values $y$ for $x=1, \cdots, 12$. How many of these values are prime?

2. Can we conclude that this formula always generates a prime number?

Definition: Twin primes

Two prime numbers are called twin primes if they differ by $2$.

Theorem $\PageIndex{6}$ Fundamental Theorem of Arithmetic (FTA)

Let $n \in\mathbb{Z_+}$, then n can be expressed as a product of primes in a unique way. This means

$n=p_1^{n_1} p_2^{n_2} \cdots p_k^{n_k}$, where $p_1 <p_2< ... <p_k$ are primes.

Neither the fundamental theorem nor the proof shows us how to find the prime factors. We can use tests for divisibility to find prime factors whenever possible.

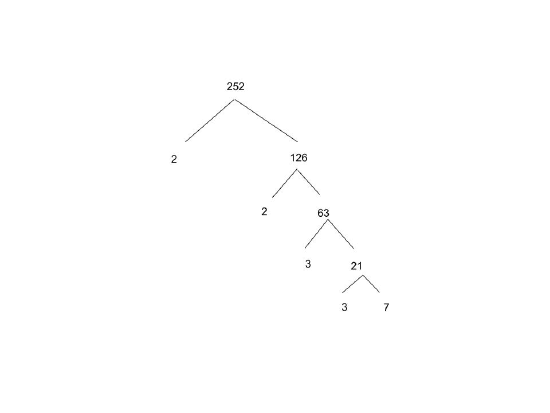
Example $\PageIndex{6}$:

Find the prime factorization of

1. $252$

2.$2018$.

3. $1000$

Solution

1. Using divisibility tests, we can find that $252= 2^2 3^2 7$

 

2. We can see that $2018$ is divisible by 2, and $2018= 2 \times 1009$. $1009$ is prime (why?).

3. $1000=10^3=((2)(5))^3=2^3 5^3$

Example $\PageIndex{7}$:

Find the prime factorization of $1000001$.

Solution

Consider $1000001=1000000+1= 10^6+1=(10^2)^3+1^3= (10^2+1^2) (10^4-10^2+1^2)= 101 \times 9901$. $101$ and $9901$ are prime (why?)

Example $\PageIndex{8}$

Determine $gcd( 2^6 \times 3^9, 2^4 \times 3^8 \times 5^2)$ and $lcm( 2^6 \times 3^9, 2^4 \times 3^8 \times 5^2)$.

Solution

$gcd( 2^6 \times 3^9, 2^4 \times 3^8 \times 5^2)= 2^4 \times 3^8$ (the lowest powers of all prime factors that appear in both factorizations) and $lcm( 2^6 \times 3^9, 2^4 \times 3^8 \times 5^2)= 2^6 \times 3^9 \times 5^2$ (the largest powers of each prime factors that appear in factorizations).

 

Note: Conjectures

Goldbach's Conjecture(1742)

Every even integer $n >2$ is the sum of two primes.

Goldbach's Ternary Conjecture:

Every odd integer $n \geq 5$ is the sum of at most three primes.

 Wilson's Theorem

Theorem $\PageIndex{7}$

Let $p$ be a prime number. Then $(p - 1)! + 1$ is divisible by $p$.

Proof:

Consider the product $P = 1 \cdot 2 \cdot 3 \cdots (p-1)$. Now, let's pair each number $k$ from $1$ to $p-1$ with its modular inverse $k^{-1}$ modulo $p$. 

We know that for every $k$ such that $1 \leq k \leq p-1$, there exists a unique $k^{-1}$ such that $kk^{-1} \equiv 1 \pmod{p}$. Moreover, these pairs will be distinct because if $kk^{-1} \equiv 1 \pmod{p}$ and $jj^{-1} \equiv 1 \pmod{p}$ for $k \neq j$, then $k = kj^{-1}$ and $j = jk^{-1}$, implying $k = j$, which contradicts the distinctness of the pairs. 

Thus, we can pair each $k$ with $k^{-1}$ such that the product of these pairs is congruent to $1 \pmod{p}$. Therefore, $P \equiv (p-1)! \equiv -1 \pmod{p}$. Adding $1$ to both sides gives $(p-1)! + 1 \equiv 0 \pmod{p}$, which means $(p-1)! + 1$ is divisible by $p$.

 

 

Fermat's Little Theorem

Theorem $\PageIndex{8}$

 For any prime number $p$ and any positive integer $a$ such that $p$ does not divide $a$, we have $a^{p-1} \equiv 1 \pmod{p}$.

Euler's Theorem

Theorem $\PageIndex{9}$

If $a$ and $n$ are relatively prime (i.e., $\gcd(a, n) = 1$), then $$a^{\phi(n)} \equiv 1 \pmod{n}$$

The following results will help us find Euler's totient function$\phi(n)$ for $n\in \mathbb{N}$.

Theorem $\PageIndex{10}$

 

1.  If $p$ is prime then $\phi(p)=p-1.$

2. If $p$ is prime and $k$ is a positive integer then $\phi(p^k)=p^k-p^{k-1}.$

3. If $m$ and $n$ are relatively prime, then $\phi(mn)=\phi(m)\phi(n).$

4.  $$\phi(n) = n \times \prod_{p|n} \left(1 - \frac{1}{p}\right)$$ where the product is taken over distinct prime factors $p$ of $n.$

 

Example $\PageIndex{9}$

Find $\phi(252)$.

Solution

Since $252= 2^2 3^2 7$, $\phi(252)=(2^2-2)(3^2-3)(7-1)=72$.