2.4: Cyclic groups

Order of group element

Definition: order of an element

Let $(G,\star)$ be a group.

Let $a \in G$, then the order of an element $a \in G$, denoted by $|a|$, be the smallest positive integer $n$ s.t. $a^n=e$.  If no such $n$ exists, we say that the order is infinite. 

Example $\PageIndex{1}$

Consider the group $\mathbb{Z}_{10}$ with addition modulo $10.$  What is the order of its elements?

Consider  $\mathbb{Z}_{10}=\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}$.   Note that $\{0\}$ is the identity and its order is $1.$ 

element	Order	Calculations
0	$|\langle 0 \rangle |=1$
1	$|\langle 1 \rangle |=10$	$1^{10}\equiv 0 \pmod{10}$
2	$|\langle 2 \rangle |=5$	$2^{1}\equiv 2\pmod{10}$, $2^2 \equiv 4 \pmod{10}$, $2^{3}\equiv 6 \pmod{10}$, $2^{4} \equiv 8 \pmod{10}$, and $2^{5}\equiv 0 \pmod{10}$.
3	$|\langle 3 \rangle |=10$	$3^1\equiv 3 \pmod{10}$, $3^2\equiv 6 \pmod{10}$ , $3^3\equiv 9 \pmod{10}$, $3^4\equiv 2 \pmod{10}$, $3^5\equiv 5 \pmod{10}$, $3^6\equiv 8 \pmod{10}$, $3^7\equiv 1 \pmod{10}$, $3^8\equiv 4 \pmod{10}$, $3^9\equiv 7 \pmod{10}$, and  $3^{10}\equiv 0 \pmod{10}$.
4	$|\langle 4 \rangle |=5$	$4^1 \equiv 4 \pmod{10}$, $4^2 \equiv 8 \pmod{10}$, $4^3 \equiv 2 \pmod{10}$, $4^4 \equiv 6 \pmod{10}$, and $4^5 \equiv 0 \pmod{10}$.
5	$|\langle 5 \rangle |=2$	$5^1 \equiv 5 \pmod{10}$, and $5^2 \equiv 0 \pmod{10}$.
6	$|\langle 6 \rangle |=5$	$6^1 \equiv 6 \pmod{10}$, $6^2 \equiv 2 \pmod{10}$, $6^3 \equiv 8 \pmod{10}$, $6^4 \equiv 4 \pmod{10}$ and $6^5 \equiv 0 \pmod{10}$.
7	$|\langle 7 \rangle |=10$	$7^1 \equiv 7 \pmod{10}$, $7^2 \equiv 4 \pmod{10}$, $7^3 \equiv 1 \pmod{10}$, $7^4 \equiv 8 \pmod{10}$, $7^5 \equiv 5 \pmod{10}$, $7^6 \equiv 2 \pmod{10}$, $7^7 \equiv 9 \pmod{10}$, $7^8 \equiv 6 \pmod{10}$, $7^9 \equiv 3 \pmod{10}$, and $7^{10} \equiv 0 \pmod{10}$.
8	$|\langle 8 \rangle |=5$	$8^1 \equiv 8 \pmod{10}$, $8^2 \equiv 6 \pmod{10}$, $8^3 \equiv 4 \pmod{10}$, $8^4 \equiv 2 \pmod{10}$, and  $8^5 \equiv 0 \pmod{10}$.
9	$|\langle 9 \rangle |=10$	$9^1 \equiv 9 \pmod{10}$, $9^2 \equiv 8 \pmod{10}$, $9^3 \equiv 7 \pmod{10}$, $9^4 \equiv 6 \pmod{10}$, $9^5 \equiv 5 \pmod{10}$, $9^6 \equiv 4 \pmod{10}$, $9^7 \equiv 3 \pmod{10}$, $9^8 \equiv 2 \pmod{10}$, $9^9 \equiv 1 \pmod{10}$,  and $9^{10} \equiv 0 \pmod{10}$.

Caution:Order

The order of a group is the number of elements in the group.

The order of an element $a \in G$, denoted by $|a|$, be the smallest positive integer $n$ s.t. $a^n=e$.

 

Definition: 

Let $(G,\star)$ be a group.

Let $X=\{x_1, x_2 \dots, x_n\}$ where $x_1, x_2 \dots, x_n \in G$, then the subset  of $G$ generated by $X$ denoted by $\langle X \rangle$ is

$\left\{x_1^{m_1} x_2^{m_2} \cdots x_n^{m_n} \mid m_1, m_2 \cdots, m_n \in \mathbb{Z} \right\}.$

 

Definition: 

Let $(G,\star)$ be a group.

Let $a \in G$, then define the set generated by $a$ denoted by $\langle a \rangle$ is $\{a^m|m\in \mathbb{Z}\}=\{\cdots, a^{-2}, a^{-1}, e, a, a^2, \cdots\}$.

Note: $a^0=e$.

Theorem $\PageIndex{1}$

Let $(G,\star)$ be a group.

Let $a \in G$, then $\langle a \rangle$ is the smallest subgroup  of $G$ that contains $a$.

Proof

Let $(G,\star)$ be a group. Let $a \in G$. If $a=e$ then $\langle a \rangle =\{e\}$ is the smallest subgroup  of $G$ that contains $e$.

Suppose $a \ne e.$ Clearly $e \in \langle a \rangle.$  Let  $g,h \in \langle a \rangle.$ Then $g=a^m$ for some $m\in \mathbb{Z}$ and $h=a^n$ for some $n \in \mathbb{Z}$. 

Consider $gh^{-1}=a^m \left(a^n\right)^{-1}=a^m a^{-n}=a^{m-n}.$ Since $m-n \in \mathbb{Z}$, $gh^{-1} \in \langle a \rangle.$

Thus, $\langle a \rangle \leq G.$ Suppose $H$ is a subgroup of G that contains $a$. Clearly, $\langle a \rangle  \leq H.$  $\square$

Note

Let $(G,\star)$ be a group.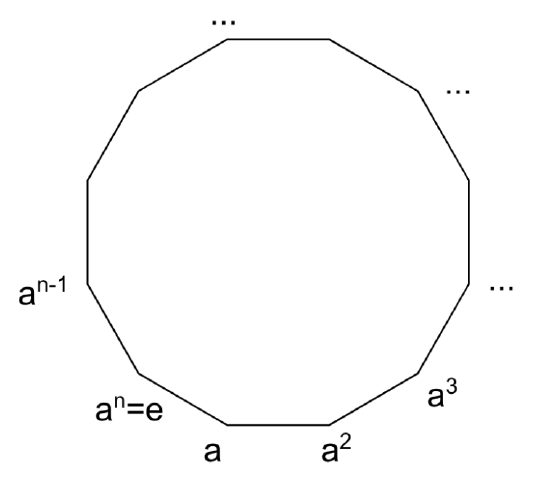

Let $a \in G$, then $\langle a \rangle$ is called cyclic subgroup of $G.$

 Cyclic group

Definition: Cyclic group

If  $G=\langle a \rangle$  for some $a \in G$, then $G$ is called a cyclic group.

Remember the definition of a unitary group:

Let $n$ be a positive integer.  Then define $U(n)=\{a \in \mathbb{Z}_+| \gcd(a,n)=1\}.$ Then $(U(n), \cdot \pmod n)$ is an abelian group. $U(n)$ is a unitary group of order $|\phi(n)|$ .

Example $\PageIndex{2}$

$U(15)=\{1,2,4,7,8,11,13,14\}$ and $\star= \cdot \pmod{15}$.

Let $a \in U(15)$ and $b \in U(15)$.

Then $a(x)+15(y)=1$ and $ab(x)+15by=b$  therefore $U(15)$ is closed.

Since $U(15)$ is a finite group, the order of the group is $|U(15)|=8$.

However, $U(15)$ is not a cyclic group. 

Proof: (by exhaustion)

Let $a \in U(15)$.

We will show that $\not \exists a \in U(15)$, s.t. $| \langle a \rangle |=8$.

$|\langle1 \rangle |=1$ since $1^1 \equiv 1 \pmod{15}$

$|\langle2 \rangle |=4$ since $2^4 \equiv 1 \pmod{15}$

$|\langle4 \rangle |=2$ since $4^2 \equiv 1 \pmod{15}$

$|\langle7 \rangle |=4$ since $7^4 \equiv 1 \pmod{15}$.

  $|\langle8 \rangle |=4$ since $8^4 \equiv 1 \pmod{15}$.

$|\langle11 \rangle |=2$ since $11^2 \equiv 1 \pmod{15}$.

$|\langle13 \rangle |=4$ since $13^4 \equiv 1 \pmod{15}$.

$|\langle14 \rangle |=2$ since $14^2 \equiv 1 \pmod{15}$.

Since $\not \exists a \in U(15)$, s.t. $|\langle a \rangle |=8$, $U(15)$ is not a cyclic group.◻

 

 

Example $\PageIndex{3}$

Prove that $(U(14),(\cdot \pmod{14}))$ is cyclic. 

Proof:

We will show that $\exists a \in U(14)$ s.t. $|\langle a \rangle |=|U(14)|$.

Consider  $U(14)=\{1,3,5,9,11,13\}$ where $|U(14)|=6$.

Consider $3^1\equiv 3 \pmod{14}$, $3^2\equiv 9 \pmod{14}$, $3^3 \equiv 13 \pmod{14}$,  $3^4\equiv 11 \pmod{14}$,  $3^5\equiv 5 \pmod{14}$ and $3^6 \equiv 1 \pmod{14}$.

$|\langle3 \rangle |=6$ since $3^6 \equiv 1 \pmod{14}$.

Thus $|\langle3 \rangle |=6$.

Therefore, $U(14)$ is cyclic and $3$ is a generator.◻

 

The following is an infinite cyclic group. Any infinite cyclic group is isomorphic to this group.

Example $\PageIndex{4}$

Is $(\mathbb{Z},+)$ cyclic group?  If so, what are the possible generators?

Yes, $(\mathbb{Z},+)$ is a cyclic group that is generated by $\pm 1$.

Proof of being a cyclic group:

Since the group generated by $1$ contains $1,$  the identity  $0,$  and the inverse of $1, (-1),$ as well as all multiples of $1$ and $(-1)$, $(\mathbb{Z},+)$ is cyclic.

 

Possible Generators:

Note $1^n$ is $1+1+\cdots+1$ with $n$ terms when $n \rangle 0$ and $(-1)+(-1)+\cdots+(-1)$ with $n$ terms when $n$ is $\langle0$.

We shall show $\mathbb{Z}=\langle1 \rangle =\langle-1 \rangle$.

Consider that $1^n$ means $1+1+\cdots +1$ with $n$ terms and that $1^{-n}$ means $+(-1)+(-1)+\cdots+(-1)$ with $n$ terms.  

It should be clear that $1^n$ will generate $\mathbb{Z}_+$ and that $1^{-n}$ will generate $\mathbb{Z}_-$.  Note that $1^0$ is interpreted as $0\cdot 1=0$.  

$\langle1 \rangle =\{ \ldots, -3,-2,-1,0,1,2,3,\ldots \}$.

Thus $\langle1 \rangle$ is a generator of $(\mathbb{Z},+)$.

Similarly, we will show that $\langle-1 \rangle$ is a generator of $(\mathbb{Z},+)$.

 Consider that $(-1)^n$ means $+(-1)+(-1)+\cdots+(-1)$ with $n$ terms and that $1^{-n}$ means $1+1+\cdots +1$ with $n$ terms.  

It should be clear that $1^n$ will generate $\mathbb{Z}_-$ and that $1^{-n}$ will generate $\mathbb{Z}_+$.  $\langle-1 \rangle =\{ \ldots, -3,-2,-1,0,1,2,3,\ldots \}$.

Thus the generators of $(\mathbb{Z},+)$ are $\langle1 \rangle$ and $\langle-1 \rangle$.

Properties: 

Theorem $\PageIndex{2}$

Cyclic groups are abelian.

Proof:

Let $(G,\star)$ be a group.

If $G$ is cyclic, then $G$ is abelian.

Assume that $G$ is cyclic.

Then $G=\langle g \rangle$ for some $g \in G$.

Let $a,b \in G$.

We will show $ab=ba$.

Then $a=g^m$ and $b=g^n$, $m,n \in \mathbb{Z}$.

Consider  $$\begin{align*} ab &=g^mg^n\\&=g^{m+n}\\&=g^{n+m}\\&=g^ng^m\\&=ba. \end{align*}$$

Hence, $G$ is abelian.◻

Note

The converse is not true.  Specifically, if a group is abelian, it is not necessarily cyclic.  A counterexample is $(U(15), \bullet)$ since it is abelian but not cyclic.

 

Theorem $\PageIndex{3}$

Every subgroup of a cyclic group will be cyclic.

Let $(G, \star)$ be a cyclic group.  If $H \le G$, then $H$ is a cyclic group.

Proof

Let $G=\langle g \rangle , \; g \in G$.

We will show $H=\langle g^k \rangle$ for some $k \in \mathbb{Z}$.

There are two cases to consider.

Case 1:  $H=\{e\}$

Let $H=\{e\}$, then we are done since $e \star e=e$ thus $|H|=|\langle e \rangle |=1$.

Case 2:  $H \ne \{e\}$ 

Let $H \ne \{e\}$.

Thus $\exists h \in H$ s.t. $h \ne e$.

Since $h \in H$, $h \in G$.

Hence $h=g^m$ for some $m \in \mathbb{Z}$.  

Without loss of generality, we may assume $m \in \mathbb{N}$.

Define $S=\{n\in \mathbb{N}|g^n \in H\} \subseteq \mathbb{N}$.

Since $S(\ne \{\})$ by the well ordering principle $S$ has a smallest element $k$.

We shall show that $H=\langle g^k \rangle$.

Since $g^k \in H$, $\langle g^k \rangle \le H$.

Let $h \in H$.

We shall show that $h \in \langle g^k \rangle$.

Since $h \in H$, $h=g^m, m \in \mathbb{Z}$.

Since $k,m \in \mathbb{Z}$, by the division algorithm, there exists $q,r$ s.t. $m=qk+r, \; 0\le r<k$.

Then $g^m=g^{qk}g^r$ and $g^{m-qk}=g^r$.

Since $g^m, g^{qk} \in H$, then $g^r \in H$.

Since $k$ is the smallest, $r=0$.  (I think this is because $g^0=e$)

Therefore $g^m=(g^k)^q \in \langle g^k \rangle$.

Thus $H \le \langle g^k \rangle$.◻

 

Note

The Converse is not true. Every sub-group of the Klein 4-group is cyclic, but not the group.

Corollary $\PageIndex{4}$

Subgroups of $(\mathbb{Z}, +)$ are of the form $(n\mathbb{Z},+)$, $n\in \mathbb{N}$.

Theorem $\PageIndex{5}$

Let $G$ be a cyclic group s.t. $G=\langle a \rangle$ and $|G|=n$.

Then $a^k=e$ iff $n|k$.

Proof

Let $G=\langle a \rangle$ with $a^n=e$.

$\langle a \rangle =\{e,a,a^2\ldots,a^{n-1}\}$.

Let $a^k=e, \; k \in \mathbb{Z}$.

Since by the division algorithm, unique integers q and r exist such that   $k=nq+r, \; 0\le r< n, \; q,r \in \mathbb{Z}$.

Consider $a^r=a^{k-nq}$ 

        $=a^k(a^n)^{-q}$ Note: $a^k=e$ is our assumption & $n$ is the order of group.

        $=ee^{-q}$

        $=e$.

Hence $r=0$.

Thus $k=nq$.

Therefore $n|k$. 

Conversely, assume that $n|k$.

Then $k=nm, m \in \mathbb{Z}$.

$a^k=a^{nm}$.

     $=(a^n)^m$

     $=e^m$

     $=e$.

Hence the result.◻

Example $\PageIndex{6}$

Consider the group $\mathbb{Z}_{12}$ with addition modulo $12.$ 

1. Is $(\mathbb{Z}_{12} ,+ mod (12) )$ cyclic group?  If so, what are the possible generators? How many distinct generators are there? What can you say about the number of generators (hint: Euler totient number) and the possible generators (Hint: Divisors)?

3. Find all subgroups of $\mathbb{Z}_{12}$ generated by each element. What are the orders of them?  What can you say about these orders?

Answer

1. Consider  $\mathbb{Z}_{12}=\{0, 1, 2, 3, 4, 5, 6, 7,  8, 9, 10, 11\}$ with addition modulo $12.$  Note that $\{0\}$ is the identity and its order is $1.$ 

Element	Order	Calculations
$0$	$|\langle 0 \rangle |=1$
$1$	$|\langle 1 \rangle |=12$	$1^{12}\equiv 0 \pmod{12}$
$2$	$|\langle 2 \rangle |=6$	$2^{1}\equiv 2\pmod{12}$, $2^2 \equiv 4 \pmod{12}$, $2^{3}\equiv 6 \pmod{12}$, $2^{4} \equiv 8 \pmod{12}$, $2^{5}\equiv 10 \pmod{12}$ and $2^{6}\equiv 0 \pmod{12}$.
$3$	$|\langle 3 \rangle |=4$	$3^1\equiv 3 \pmod{12}$, $3^2\equiv 6 \pmod{12}$ , $3^3\equiv 9 \pmod{12}$, and $3^4\equiv 0 \pmod{12}$.
$4$	$|\langle 4 \rangle |=3$	$4^1 \equiv 4 \pmod{12}$, $4^2 \equiv 8 \pmod{12}$,  and $4^3 \equiv 0 \pmod{12}$.
$5$	$|\langle 5 \rangle |=12$	$5^1 \equiv 5 \pmod{12}$,  $5^2 \equiv 10 \pmod{12}$, $5^3 \equiv 3 \pmod{12}$,  $5^4\equiv 8 \pmod{12}$, $5^5 \equiv 1 \pmod{12}$,  $5^6 \equiv 6 \pmod{12}$, $5^7 \equiv 11 \pmod{12}$,  $5^8 \equiv 4 \pmod{12}$,$5^9 \equiv 9 \pmod{12}$,  $5^{10} \equiv 2 \pmod{12}$, $5^{11} \equiv 7 \pmod{12}$, and  $5^{12} \equiv 0 \pmod{12}$.
$6$	$|\langle 6 \rangle |=2$	$6^1 \equiv 6 \pmod{12}$, and $6^2 \equiv 2 \pmod{12}$.
$7$	$|\langle 7 \rangle |=12$	$7^1 \equiv 7 \pmod{12}$, $7^2 \equiv 2 \pmod{12}$, $7^3 \equiv 9 \pmod{12}$, $7^4 \equiv 4 \pmod{12}$, $7^5 \equiv 11 \pmod{12}$, $7^6 \equiv 6 \pmod{12}$, $7^7 \equiv 1 \pmod{12}$, $7^8 \equiv 8 \pmod{12}$, $7^9 \equiv 3 \pmod{12}$, $7^{10} \equiv 10 \pmod{12}$, $7^{11} \equiv 5 \pmod{12}$,  and  $7^{12} \equiv 0 \pmod{12}$.
$8$	$|\langle 8 \rangle |=3$	$8^1 \equiv 8 \pmod{12}$, $8^2 \equiv 4 \pmod{12}$ and $8^3 \equiv 0 \pmod{12}$.
$9$	$|\langle 9 \rangle |=4$	$9^1 \equiv 9 \pmod{12}$, $9^2 \equiv 6  \pmod{12}$, $9^3 \equiv 3 \pmod{12}$ and $9^4 \equiv 0 \pmod{12}$. $9^5 \equiv 5 \pmod{10}$, $9^6 \equiv 4 \pmod{10}$, $9^7 \equiv 3 \pmod{10}$, $9^8 \equiv 2 \pmod{10}$, $9^9 \equiv 1 \pmod{10}$,  and $9^{10} \equiv 0 \pmod{10}$.
$10$	$|\langle 10 \rangle |=6$	$10^1 \equiv 10 \pmod{12}$, $10^2 \equiv 8 \pmod{12}$, $10^3 \equiv 6 \pmod{12}$, $10^4 \equiv 4 \pmod{12}$, $10^5 \equiv 2 \pmod{12}$ and $10^6 \equiv 0 \pmod{12}$.
$11$	$|\langle 11 \rangle |=12$	$11^1 \equiv 11 \pmod{12}$, $11^2 \equiv 10 \pmod{12}$, $11^3 \equiv 9 \pmod{12}$, $11^4 \equiv 8 \pmod{12}$, $11^5 \equiv 7 \pmod{12}$, $11^6 \equiv 6 \pmod{12}$, $11^7 \equiv 5 \pmod{12}$, $11^8 \equiv 4 \pmod{12}$, $11^9 \equiv 3 \pmod{12}$, $11^{10} \equiv 2 \pmod{12}$, $11^{11} \equiv 1 \pmod{12}$,  and  $11^{12} \equiv 0 \pmod{12}$.

 From the table,   $(\mathbb{Z}_{12},+ mod (12) )$ is a cyclic group,   the set of all possible generators are $\{1, 5, 7, 11\}=\{  a \in \mathbb{Z}| gcd(a,12)=1 ,\; 1 \leq a < 12 \}$. Hence, the number of generators is the same as the number of integers relatively prime to $12=2^2\,3$.  That is, the number of generators is the Euler totient number $\phi(12) =(2^2-2)(3^1-1)= 4 \;\; .$

2. From the above table, we see that the orders of the subgroups are  $1, 2, 3, 4, 6$ and 12, which are all divisors of the order of  $\mathbb{Z}_{12}$. Specifically, the order of the subgroup generated by $g \in \mathbb{Z}_{12}$  is $\dfrac{n}{ gcd(g, n)}.$

Note that $12=2^2 \, 3$. Then the cyclic subgroups are $\langle 1 \rangle , \langle 6 \rangle , \langle 4 \rangle , \langle 3 \rangle , \langle 2 \rangle , \langle 0 \rangle$ with orders $12, 2, 3, 4, 6$ and $1.$

 

Theorem $\PageIndex{6}$

$\langle a^k \rangle =\langle a^{\gcd(n,k)} \rangle$

Let $G=\langle a \rangle$ be a cyclic group with $|G|=n$.

Let $b \in G$.

If $b=a^k$ then $|b|=\frac{n}{d}, \; d=\gcd(k,n)$.

 

Answer

Let $G=\langle a \rangle$ with $|G|=n$ and $a \in G$.

Let $a^n=e$.

We will show that $\langle a^k \rangle =\langle a^{\gcd{(n,k)}} \rangle$.

Let $x \in \langle a^k \rangle$.

Since $\gcd(n,k)=d$ for some $d \in \mathbb{Z}_+$, $d|n$ and $d|k$.

Thus, $k=md, m\in \mathbb{Z}$.

Consider an arbitrary power of $a^k$, $(a^k)^j \in \langle a^k \rangle$.

$(a^k)^j = (a^{md})^j=(a^d)^{jm} \in \langle a^d \rangle \in \langle a^{\gcd{(n,k)}} \rangle$.

Let $d=xn+yk, \; n,k \in \mathbb{Z}$.

Using the division algorithm, $(a^{xn+yk})^h= (a^n)^{xh} (a^k)^{yh}, \;n,k,h \in \mathbb{Z}$

    $=(a^k)^{yh} \in \langle a^k \rangle$.

Thus $a^k = a^d$.

Now we want to show $|a^k|=\frac{n}{d}$.

Consider $(a^k)^{\frac{n}{d}}=(a^n)^{\frac{k}{d}}=e^{\frac{k}{d}}=e$.

Thus $|a^k|\le \frac{n}{d}$.

Now consider $(a^d)^{\frac{n}{d}}=(a^n)=e \; \Rightarrow \; |a^d| \le \frac{n}{d}$.

Now consider $0 \le i <\frac{n}{d}$.

Thus $di< n$, where $d$ is positive since it is the greatest common denominator.

Thus $(a^d)^i=a^{di}\ne e$ for $di<n$.

Then we can show $|a^d|=\frac{n}{d}$.

Consider $|a^k|=|\langle a^k \rangle |=|\langle a^d \rangle |=|a^d|= \frac{n}{d}$.

Hence $|a^k|=\frac{n}{d}$.

Theorem $\PageIndex{7}$

Let $G=\langle g \rangle$ be a cyclic group with $|g|=n$. Then  $G=\langle g^k \rangle$ if and only if $gcd(k,n)=1.$

Proof

Let $G=\langle g \rangle$ be a cyclic group with $|g|=n$. Then
$g \in G$  and $g^n=e$.

Assume that  $G = \langle g^k \rangle$. Then $g = (g^k)^ x$ for some $x \in \mathbb{Z}$. 

Thus,
$g^{1 - kx} = e.$
By Theorem 2.4.5,  $n \mid (1 - kx)$. Therefore, 
$1 - kx = ny,$ for some $y \in \mathbb{Z}.$
Which implies,
$1 = kx + ny,$
hence,
$\gcd(k, n) = 1.$

Conversly, we  shall show that if $\gcd(k, n) = 1$, then $G = \langle g^k \rangle$. 
Suppose that  $\gcd(k, n) = 1$. Then 
$kx + ny = 1$, for some $x, y \in \mathbb{Z}.$
By using the properties of powers in a group and $g^n=e$, we get,
$$g^1 = g^{kx + ny}=(g^k)^x  (g^n)^y=(g^k)^x.$$

Hence $g \in \langle g^k \rangle$.

Therefore, we have $G \subseteq \langle g^k \rangle$. Since $\langle g^k \rangle \ \subseteq G$, 
$G = \langle g^k \rangle.$

 

Theorem $\PageIndex{8}$: 

Let $G=\langle a \rangle$ be a cyclic group with $|G|=n$. Prove the following statements:

a) If $H\leq G$ then $H=\langle a^k \rangle$ for some integer $k$ that divides $n$.

b) If $k|n$ then $\langle a^{\frac{n}{k}} \rangle$ is the unique subgroup of $G$ of order $k$.

Proof

a)  Let $G = \langle a \rangle$ with $|G| = n.$ Assume that $H\leq G$. By Theorem 2.4.3, $H$ is cyclic. Hence  $H=\langle a^k \rangle$ for some integer $k \in \textbf{Z}.$  Let $d=gcd(k,n)$.  We shall show that $H=\langle a^d \rangle$. Since $d=gcd(k,n)$, $kx + ny = d$, for some $x, y \in \mathbb{Z}.$   Consider, $$a^d = a^{kx + ny}=(a^k)^x  (a^n)^y=(a^k)^x.$$ Thus $a^d \in H$. Therefore $\langle a^d \rangle \subseteq H.$
Since $d|k, k=md,$ for some $m\in \mathbb{Z}.$ Thus, $a^k=a^{md}=\left(a^d\right)^m.$ Hence $H \subseteq \langle a^d \rangle$. Thus $H =\langle a^d \rangle$ and $d|n.$

b) Let $G = \langle a \rangle$ with $|G| = n.$ Assume that $k|n$. Suppose $K$ be subgroup of $G$ of order $k$. We shall show that  $K=\langle a^{\frac{n}{k}} \rangle$. Since $K$ is a subgroup of $G$, $K=\langle a^m  \rangle$, for some, $m \in \mathbb{Z}.$ By part a, $m|n.$ Then $\left(a^m\right)^{n/m}=e$. We shall show that $\dfrac{n}{m}$ is the smallest positive integer with this property.

 

Now, $|K|= \dfrac{n}{m}=k$. Thus, $m=\dfrac{n}{k}$. Thus $K= \langle a^\frac{n}{k} \rangle$ which is unique.

 

Theorem $\PageIndex{9}$

A group of prime order is cyclic.

Proof

Let $G$ be a group s.t. $|G|=p$, where $p$ is a prime number.
Let $g \in G$ s.t. $H=\langle g \rangle$ is a subgroup of $G$.

Since $p > 1$, $g \ne \{e\}$.

Since $H$ is cyclic,  $\exists \; g^k=e$, for some $k \in \mathbb{Z}$.  

By the division algorithm, $k=nq+r$ where $0 \le r < n$.

Hence, $e=g^k=g^{nq+r}=g^{nq}g^r=eg^r=g^r$.

Since the smallest positive integer $k$ such that $g^k=e$ is $n$, $r=0$.  Thus $n|k$.

Conversely, if $n|k$, then $k=nm$, $m \in \mathbb{Z}$. 

Consequently, $g^k=g^{nm}=(g^n)^m=e^m=e$.

Thus, $|\langle g \rangle |$ divides $|G|$.

Consider that the only two divisors of a prime number are the prime number itself and 1.

Since $p < 1$, $|G|=p$.

Since $|G|=p$, $G$ is cyclic.◻

 

 

Example $\PageIndex{7}$

List all the cyclic subgroups of $U(30)$.

$U(30)=\{1,7,11,13,17,19,23,29\}$ and  $|U(30)|=8$.

$k$	Calculations	$|k|$
7	$7^1 \equiv 7 \pmod{30}$, $7^2 \equiv 19 \pmod{30}$, $7^3 \equiv 13 \pmod{30}$, $7^4 \equiv 1 \pmod{30}$	4
11	$11^1 \equiv 11 \pmod{30}$, $11^2 \equiv 1 \pmod{30}$	2
13	$13^1 \equiv 13 \pmod{30}$, $13^2 \equiv 19 \pmod{30}$, $13^3 \equiv 7 \pmod{30}$, $13^4 \equiv 1 \pmod{30}$	4
17	$17^1 \equiv 17 \pmod{30}$, $17^2 \equiv 19 \pmod{30}$, $17^3 \equiv 23 \pmod{30}$, $17^4 \equiv 1 \pmod{30}$	4
19	$19^1 \equiv 19 \pmod{30}$, $19^2 \equiv 1 \pmod{30}$	2
23	$23^1 \equiv 23 \pmod{30}$, $23^2 \equiv 19 \pmod{30}$, $23^3 \equiv 17 \pmod{30}$,  $23^4 \equiv 1 \pmod{30}$	4
29	$29^1 \equiv 29 \pmod{30}$, $29^2 \equiv 1 \pmod{30}$	2

 

Since $\not \exists a \in U(30)$ s.t. $|\langle a \rangle |=|U(30)|=8$, $U(30)$ is not a cyclic group.

However the following subgroups of $U(30)$ are cyclic: $\{1,7,13,19\}$, $\{1,17,19,23\}$, $\{1,11\}$,  $\{1,19\}$, $\{1,29\}$ and $\{1\}$.

 

Theorem $\PageIndex{10}$: Primitive Root Theorem

Let $n \geq 1.$ Then $U(n)$ is cyclic iff $n=1, 2, 4, p^k$ or $2p^k$ where $p$ is an odd prime and $k \geq 1.$

 

Note

$U(n)$ is not  cyclic if $n$ is divisible by two distinct odd primes or by $4$ and an odd prime.

Example $\PageIndex{8}$

$U(1), U(2), U(3), U(4), U(5), U(6), U(7), U(9), U(10), U(11), U(18), U(27)$ are cyclic.

$U(8), U(16), U(20), U(30)$ are not cyclic.