1.2: Greatest common divisor and least common multiple

Think out loud

We want to tile a \(253\) ft by \(123\) ft (\(a=253\) and \(b=123,\) with \(a, b \in \mathbb{Z} \)) floor with identical square tiles. What is the largest square tile we can use?

Definition: Greatest Common Divisor

Let \(a,b \in \mathbb{Z}\), where  not  both \(a,b\)  is zero.

Then, we say that an integer \(d=\gcd(a,b) \in \mathbb{Z_+}\)., greatest common divisor if it satisfies the following conditions:

1. \(d|a\) and \(d|b\), Note: \(d\) must divide both numbers

2. If \(c \in \mathbb{Z}\), \(c|a\) and \(c|b\) then \(c\le d\). Note: \(d\) is the greatest number divides both.

Thus, the greatest common divisor of two integers \(a\) and \(b\), also known as GCD of \(a\) and \(b\), is the greatest positive integer that divides both the integers \(a\) and \(b\). This class will use the following notation: \(\gcd (a,b)\).

Example \(\PageIndex{1}\):

What is the \(\gcd\) of \(15\) and \(20\)?

A process to find the solution:
List all positive divisors of \(15\) and \(20\).
The positive divisors of \(15\) are \(1, 3, 5,\) and \(15\).
The positive divisors of \(20\) are \(1, 2, 4, 5, 10,\) and \(20\).
The common positive divisors are \(1, 5\).
As you can see from the list the gcd of \(15\) and \(20\) is \(5.\) That is, the \( \gcd(15, 20)=5.\)

Example \(\PageIndex{2}\):

An elementary gym teacher has \( 3\) grade \(4\) gym classes with \(21, 35\) and \(28\) students in them. The teacher wants to order equipment that equal-sized groups can use in each class. What is the largest group size that will work for all \(3\) classes?

Solution:
You will need to find the GCD of all \(3\) classes.
Firstly, you will find the GCD of \(21\) and \(35.\)
The positive divisors of \(21\) are \(1, 3, 7,\) and \(21\).
The positive divisors of \(35\) are \(1, 5, 7,\) and \(35\).
The GCD of \(21\) and \(35\) is \(7.\)

Since \(7 \mid 28\) you will now find the GCD of \(7\) and \(28\), which turns out to be 7.
Therefore the GCD of \( 21, 35 \) and \(28\) is \(7. \)
Thus, the largest number of students in a group for each class will be \(7.\)

Properties:

Let \(a,b,c \in \mathbb{Z}\). 

Then:

1. \(\gcd(a, a)=|a|, a\ne 0.\)
2. \(\gcd(a, b)=\gcd(b, a)\).
3. \(\gcd(a,b,c)=\gcd (\gcd(a, b), c)=\gcd (a, \gcd(b, c))\).
4. \(\gcd(a, 0)=a\).
5. \(\gcd(0, 0)\) is undefined.

Now, let's explore an algorithm for determining the GCD. The Euclidean Algorithm, developed by the renowned Greek mathematician Euclid, is a highly effective method for computing the GCD of two integers.

Definition:   Euclidean Algorithm

If \(a,b \in \mathbb{Z} \setminus \{0\}\), then by using division algorithm iteratively, we obtain

\begin{eqnarray*}a &=bq_0+r_0 \\ b &=r_0 q_1+r_1 \\  r_0 &=r_1q_2+r_2\\ \vdots \\ r_{n-2} &=r_{n-1}q_{n}+r_n \\ r_{n}&=r_nq_{n+1}+0 \\ \end{eqnarray*}

Notice that, the last non-zero remainder is \(r_{n}\), such an \(r_n\) exists, since \(|b|>|r_0|>|r_1| \cdots >|r_n|.\) The \(r_n=\gcd(a,b)\).

 

 

Example \(\PageIndex{3}\)

Find \(\gcd(2420, 230)\).

Note: Work from right to left to follow the steps shown in the image below.

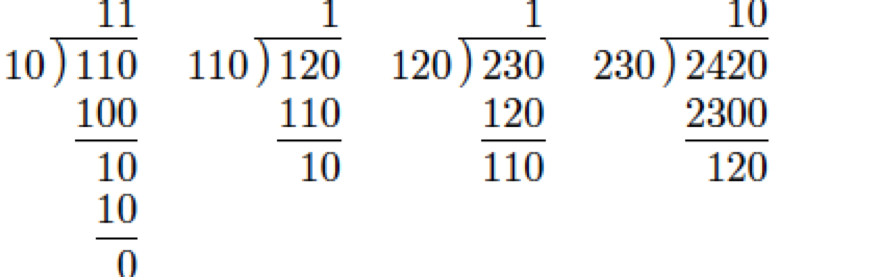
Hence, \(\gcd(2420,230) =10\).

 

BEZOUT'S IDENTITY

For integers a and b, let d be the greatest common divisor, d = GCD (a, b). Then there exists integers x and y such that ax+by=d. Any integer that is of the form ax+by, is a multiple of d.

Note

This condition will be a necessary and sufficient case of \(d=1\). We will prove this result in section 4.4, Relatively Prime numbers.

Example \(\PageIndex{4}\)

Write gcd as a linear combination.  \(\gcd(2071,31)=2071x+31y\), with \(x,y \in \mathbb{Z}\).

Solution

Steps are listed (a,b,c,d) for ease of reference to Bezout’s algorithm

a) \(2071=31(66)+25\)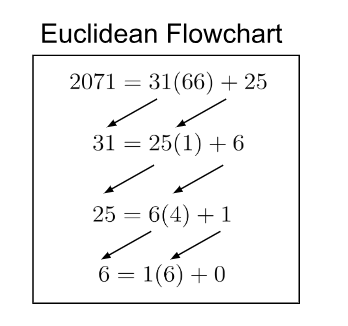

b) \(31=25(1)+6\)

c) \(25=6(4) +1\)

d) \(6=1(6)+0\).  The process stops when the remainder is zero. Thus, \(\gcd =1\).  

 

Bezout’s Algorithm

1. \(25=2071+31(-66)\)  from a) above.

2. \(6=31+25(-1)\) from b) above.

3. \(1=25 +6(-4)\) from c) above.

 

\(1=25+6(-4)\) from 3) above.

   \(=25+(31+25(-1))(-4)=25(5)+31(-4)\)  using 2) above. 

   \(=(2071 +31(-66))(5)+31(-4)\) using 1) above

  

 

Example \(\PageIndex{5}\)

Write gcd as a linear combination.  \(\gcd(3915,825)=3915x+825y\), with \(x,y \in \mathbb{Z}\).

Solution

From the calculation below,  \(\gcd(3915,825)=15.\)

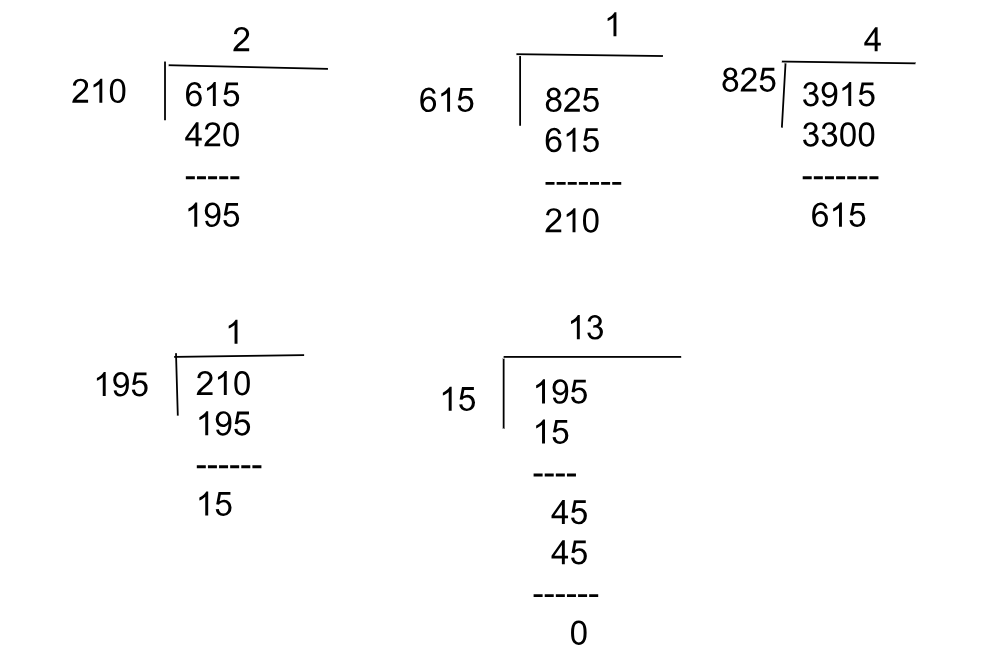
We will use the following tabular method:

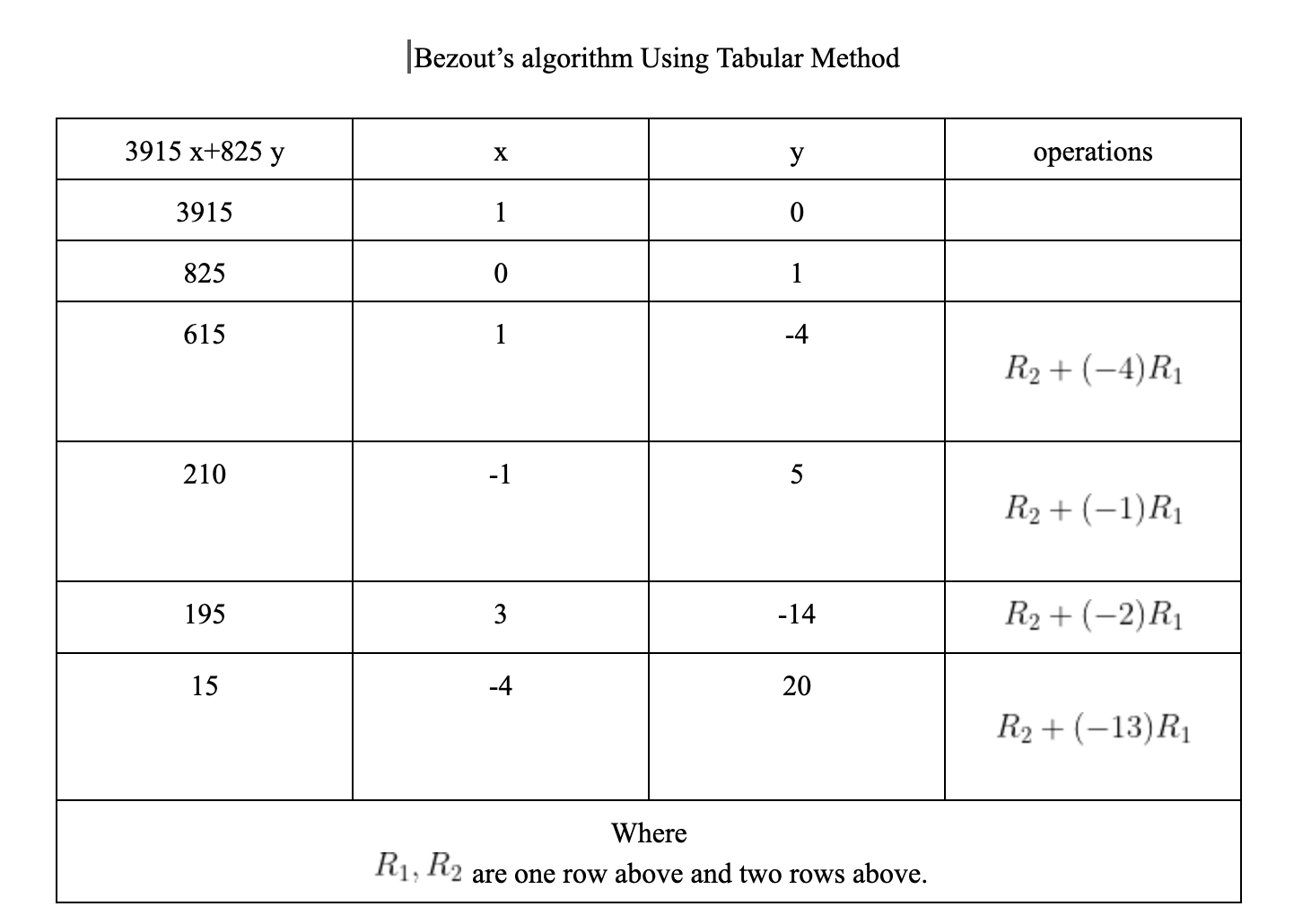
Thus,  \(\gcd(3915,825)=3915(-4)+825(20)\).

Example \(\PageIndex{6}\)

Let \(a,b \in \mathbb{Z}\backslash \{0\}\).  Prove or disprove:  \(d=ax+by\) for some \(x,y \in \mathbb{Z}\) then \(\gcd(a,b)=d\).

 

Counterexample:

Let \(d=6, \ a=2071,\) and \(b=31\).

Consider \(6=2071(-1)+31(67)\).

Further consider that \(1=2017(5)+31(-334)\).

Since \(1<6\) and 1 is the  lowest possible \(\gcd(a,b)\).

Example \(\PageIndex{7}\)

 Prove or disprove:  If \(1=ax+by\) then \(\gcd(a,b)=1\).

Proof:

Let \(a,b \in \mathbb{Z} \backslash \{0\}\) s.t. \(1=ax+by\) with \(x,y \in \mathbb{Z}.\)

Suppose \(d=\gcd(a,b)\).  We will show that \(d=1\).

Since \(d=\gcd(a,b), \;\; d|a\) and \(d|b\).

Since \(d|a, a=md, \; m \in \mathbb{Z}\).

Since \(d|b, b=nd, \; n \in \mathbb{Z}.\)

Now, \(ax+by=(md)x+(nd)y\)

\(=d(mx+ny\).

Since  \(mx, ny \in \mathbb{Z}, mx+ny \in \mathbb{Z}\).

Now \(1=ax+by=d(mx+ny)\).

Therefore \(d|1\).

Thus, \(d= \pm 1\), but since \(d\ge 0, d=1\).

Relatively prime

Definition: Relatively prime

Two integers \(a\) and \(b\) are said to be relatively prime if \(\gcd(a,b)=1\).

 

Example \(\PageIndex{8}\)

Show that \(\gcd(n,n+1)=1, \ \forall n \in \mathbb{Z}\). That is, show that any two consecutive integers are relatively prime.

Since \(n(-1)+(n+1)(1)=1\), \(\gcd(n,n+1)=1\).

 

Example \(\PageIndex{9}\)

 Find two integers \(x\) and \(y\) such that \(\gcd(-4357,3754)= -4357(x)+3754(y)\).

 

First use Euclidean Algorithm

\(-4357=3754(-2)+3151\) Note:  Remainder must be greater than or equal to zero.

\begin{eqnarray*}3754 & =3151(1)+603\\3151&= 603(5)+136\\603 & =136(4)+59\\136 & =59(2)+18\\59 & =18(3)+5\\18 & =5(3)+3\\5 & =3(1)+2\\3 & =2(1)+1\\2& =1(2)+0\\\end{eqnarray*}

Therefore \(\gcd(-4357,3754)=1.\)

 

Then use Bezout’s Algorithm.

 

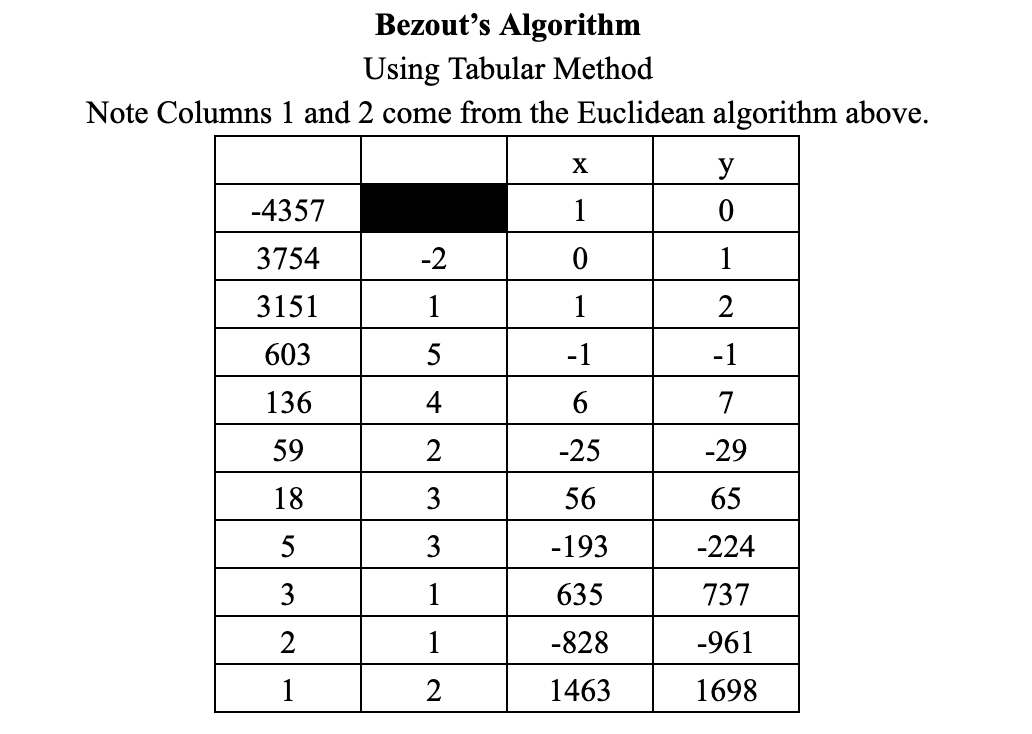
Thus \(\gcd(-4357,3754)=-4357(1463)[phone])=1.\)

Definition:  

For \(n \in \mathbb{N}\), the Euler's totient function \(\phi(n)\) is defined to be the number of positive integers less than \(n\) that are relatively prime to \(n\).

Euler's totient function has numerous applications in number theory, cryptography, and other branches of mathematics. It plays a vital role in RSA encryption, where it is used to compute the encryption and decryption keys.

Example \(\PageIndex{10}\)

Determine the value \(\phi(n)\) for each integer \(n \le  30\).  For \(n \in \mathbb{N}\), \(\phi(n)\) is defined to be the number of positive integers less than \(n\) that are relatively prime to \(n\).

Number of \(n \in \mathbb{N}\), Relatively Prime to \(n\)
\(n\)	\(\phi (n)\)	Set  of \(n \in \mathbb{N}\) that are relatively Prime to \(n\).
1	0	{}
2	1	{1}
3	2	{1,2}
4	2	{1,3}
5	4	{1,2,3,4}
6	2	{1,5}
7	6	{1,2,3,4,5,6}
8	4	{1,3,5,7}
9	6	{1,2,4,5,7,8}
10	4	{1,3,7,9}
11	10	{1,2,3, … ,8,9,10}
12	4	{1,5,7,11}
13	12	{1,2,3, … ,10,11,12}
14	6	{1,3,5,9,11,13}
15	8	{1,2,4,7,8,11,13,14}
16	8	{1,3,5,7,9,11,13,15}
17	16	{1,2,3, … ,14,15,16}
18	6	{1,5,7,11,13,17}
19	18	{1,2,3, … ,16,17,18}
20	8	{1,3,7,9,11,13,17,19}
21	12	{1,2,4,5,8,10,11,13,16,17,19,20}
22	10	{1,3,5,7,9,13,15,17,19,21}
23	22	{1,2,3, … ,20,21,22}
24	8	{1,5,7,11,13,17,19,23}
25	20	{1,2,3,4,6,7,8,9,11,12,13,14,16,17,18,19,21,22,23,24}
26	12	{1,3,5,7,9,11,15,17,19,21,23,25}
27	18	{1,2,4,5,7,8,10,11,13,14,16,17,19,20,22,23,25,26}
28	12	{1,3,5,9,11,13,15,17,19,23,25,27}
29	28	{1,2,3, … ,26,27,28}
30	8	{1,7,11,13,17,19,23,29}

Multiplicative inverse modulo m

Let \(m \in \mathbb{Z}_+.\)  Let \(a \in \mathbb{Z}\) such that \(a\) and \(m\) are relatively prime. Then there exist integers \(x\) and \(y\) such that \(ax+my=1.\) Then  \(ax \equiv 1 ( mod \,m ) \). Note that \(1\) is the multiplicative identity on \(mod \,m \). In this case, \(x (mod \,m) \) is the inverse of \(a (mod \,m)\).

Example \(\PageIndex{11}\)

If possible, find multiplicative inverse of \( 2 (\mod 10).\)

Solution

Since \(\gcd(2,10)=2 \ne 1\), \(2\) has no multiplicative inverse modulo \(10.\)

Example \(\PageIndex{12}\)

If possible, find multiplicative inverse of \( 16 (\mod 35).\)

Solution

By using Euclidean Algorithm, we will find \(gcd(16,35)\).

\begin{eqnarray*}35&=(16)(2)+3\\16&=(3)(5)+1\\3 &=(1)(3)+0\end{eqnarray*}

Thus \(gcd(16,35)=1\). Hence multiplicative inverse of \( 16 (\mod 35)\) exists.

By using Bezout's algorithm,

\begin{eqnarray*}1&=16+(3)(-5)\\&=16+(35+(16)(-2)) (-5)\\&=(35)(-5)+(16)(11)\end{eqnarray*}

Thus \(gcd(16,35)=1=(35)(-5)+(16)(11).\) Hence the multiplicative inverse of \( 16 (\mod 35)\) is \(11\).

 

  Least Common Multiples  

 

Definition: Least Common Multiples

Let \(a\) and \(b\) be integers. Then any integer that is a multiple of both \(a\) and \(b\) is called a common multiple of \(a\) and \(b\). The least common multiple of integers a and b, denoted by \(lcm(a,b)\), is the smallest positive common multiple of \(a\) and \(b\).

Example \(\PageIndex{13}\):

Find

1. \(lcm(5,10)\)

2. \(lcm(-6,18)\)

3. \(lcm(0,5)\)

Solution

1. \(10\), 2. \(18\) 3. undefined.

Finding LCM using GCD

The least common multiple of integers a and b, also known as the LCM, is the smallest number divisible by both integers a and b. You can determine the LCM by dividing the absolute value of the product of a and b by the GCD of \(a\) and \(b\).

That is
\[ lcm(a,b)= \displaystyle \frac{|ab|}{\gcd(a,b)}\]

Example \(\PageIndex{14}\):

What is the LCM of \(24\) and \( 35\)?
Solution:
We must first determine the GCD of \(24\) and \(35\).
Find the divisors of \(24\) and \(35.\)
\(24: 1, 2, 3, 4, 8, 12, 24\)
\(35: 1, 5, 7, 35\)
Therefore the GCD of \(24\) and \(35\) is \(1.\)

Now that we have determined the GCD, we can continue to determine the least common multiple.
\(\frac{(24)(35)}{1}= 840.\)

Hence \(lcm(24,35)=840.\)

Properties:

Let \(a,b,c \in \mathbb{Z}\). 

Then:

1. \(lcm(a, a)=a.\)
2. \(lcm(a, b)=lcm(b, a)\).
3. \(lcm(a,b,c)=lcm (lcm(a, b), c)=lcm(a, lcm(b, c))\).
4. \(lcm(a,0)=\) undefined.