7.5: Fitting Exponential Models to Data

Learning Objectives

• Use a graphing utility to find the exponential model that best fits the data
• Make predictions using an exponential model found with technology
• Determine if a linear or an exponential model fits the data better

in order to apply mathematical modeling to solve real-world applications.

In previous sections of this chapter, we were either given a function explicitly to graph or evaluate, or we were given a set of points that were guaranteed to lie on the curve. Then we used algebra to find the equation that fit the points exactly. In this section, we use a modeling technique called regression analysis to find a curve that models data collected from real-world observations. With regression analysis, we don’t expect all the points to lie perfectly on the curve. The idea is to find a model that best fits the data. Then we use the model to make predictions about future events.

Do not be confused by the word model. In mathematics, we often use the terms function, equation, and model interchangeably, even though they each have their own formal definition. The term model is typically used to indicate that the equation or function approximates a real-world situation.

We will concentrate on three types of regression models in this section: exponential, logarithmic, and logistic. Having already worked with each of these functions gives us an advantage. Knowing their formal definitions, the behavior of their graphs, and some of their real-world applications gives us the opportunity to deepen our understanding. As each regression model is presented, key features and definitions of its associated function are included for review. Take a moment to rethink each of these functions, reflect on the work we’ve done so far, and then explore the ways regression is used to model real-world phenomena.

Building an Exponential Model from Data

As we’ve learned, there are a multitude of situations that can be modeled by exponential functions, such as investment growth, radioactive decay, atmospheric pressure changes, and temperatures of a cooling object. What do these phenomena have in common? For one thing, all the models either increase or decrease as time moves forward. But that’s not the whole story. It’s the way data increase or decrease that helps us determine whether it is best modeled by an exponential equation. Knowing the behavior of exponential functions in general allows us to recognize when to use exponential regression, so let’s review exponential growth and decay.

Recall that exponential functions have the form \(y=ab^x\). When performing regression analysis, we use the form most commonly used on graphing utilities, \(y=ab^x\). Take a moment to reflect on the characteristics we’ve already learned about the exponential function \(y=ab^x\) (assume \(a>0\)):

• \(b\) must be greater than zero and not equal to one.
• The initial value of the model is \(y=a\).
  • If \(b>1\), the function models exponential growth. As \(x\) increases, the outputs of the model increase slowly at first, but then increase more and more rapidly, without bound.
  • If \(0<b<1\), the function models exponential decay. As \(x\) increases, the outputs for the model decrease rapidly at first and then level off to become asymptotic to the x-axis. In other words, the outputs never become equal to or less than zero.

As part of the results, your calculator will display a number known as the correlation coefficient, labeled by the variable \(r\), or \(r^2\). (You may have to change the calculator’s settings for these to be shown.) The values are an indication of the “goodness of fit” of the regression equation to the data. We more commonly use the value of \(r^2\) instead of \(r\), but the closer either value is to \(1\), the better the regression equation approximates the data.

Exponential Regression

Exponential regression is used to model situations in which growth begins slowly and then accelerates rapidly without bound, or where decay begins rapidly and then slows down to get closer and closer to zero. We use the command “ExpReg” on a graphing utility to fit an exponential function to a set of data points. We can also use desmos instead to find an exponential function that fits the data. This returns an equation of the form,

\[y=ab^x\]

Note that:

• \(b\) must be non-negative.
• when \(b>1\), we have an exponential growth model.
• when \(0<b<1\), we have an exponential decay model.

How to: Given a set of data, perform exponential regression using desmos

When using desmos, you will first, create a table and fill in the two columns with the data where the first column is x₁ and the second column is y₁. Then, type "y₁ ~ a b^x₁" and desmos will create the best fit exponential function and also give the values of a and b. Please make sure to check the box called "Log Mode" if you want demos to output the same answers as other graphing utilities.

Example \(\PageIndex{1}\): Using Exponential Regression to Fit a Model to Data

In 2007, a university study was published investigating the crash risk of alcohol impaired driving. Data from \(2,871\) crashes were used to measure the association of a person’s blood alcohol level (BAC) with the risk of being in an accident. Table \(\PageIndex{1}\) shows results from the study. The relative risk is a measure of how many times more likely a person is to crash. So, for example, a person with a BAC of \(0.09\) is \(3.54\) times as likely to crash as a person who has not been drinking alcohol.

Table \(\PageIndex{1}\)

BAC	0	0.01	0.03	0.05	0.07	0.09
Relative Risk of Crashing	1	1.03	1.06	1.38	2.09	3.54
BAC	0.11	0.13	0.15	0.17	0.19	0.21
Relative Risk of Crashing	6.41	12.6	22.1	39.05	65.32	99.78

1. Let \(x\) represent the BAC level, and let \(y\) represent the corresponding relative risk. Use exponential regression to fit a model to these data.
2. After \(6\) drinks, a person weighing \(160\) pounds will have a BAC of about \(0.16\). How many times more likely is a person with this weight to crash if they drive after having a \(6\)-pack of beer? Round to the nearest hundredth.

Solution

1. Using the STAT then EDIT menu on a graphing utility, list the BAC values in L1 and the relative risk values in L2. Then use the STATPLOT feature to verify that the scatterplot follows the exponential pattern shown in Figure \(\PageIndex{1}\):

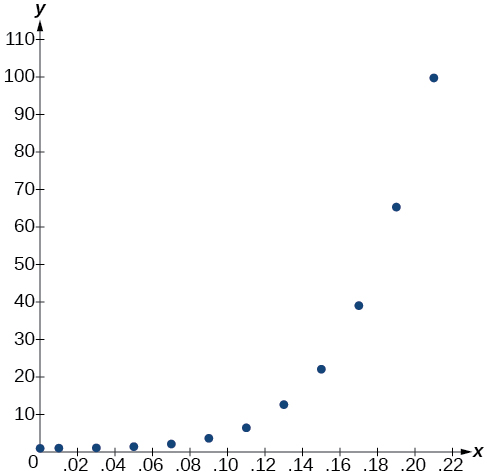
Figure \(\PageIndex{1}\)

Use the “ExpReg” command from the STAT then CALC menu to obtain the exponential model,

\(y=0.58304829{(2.20720213E10)}^x\)

Converting from scientific notation, we have:

\(y=0.58304829{(22072021300)}^x\)

Notice that \(r^2≈0.97\) which indicates the model is a good fit to the data. To see this, graph the model in the same window as the scatterplot to verify it is a good fit as shown in Figure \(\PageIndex{2}\):

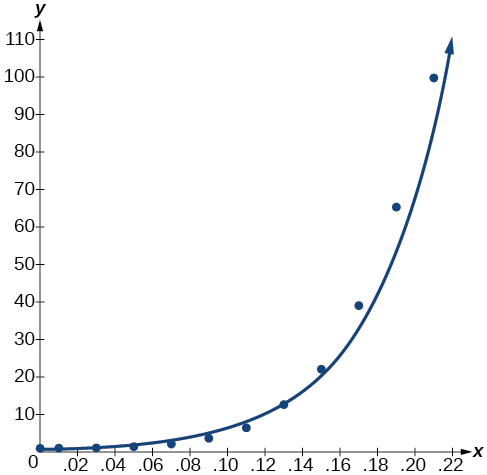
Figure \(\PageIndex{2}\)

2. Use the model to estimate the risk associated with a BAC of \(0.16\). Substitute \(0.16\) for \(x\) in the model and solve for \(y\).

\[\begin{align*} y&= 0.58304829{(22072021300)}^x \qquad \text{Use the regression model found in part } (a)\\ &= 0.58304829{(22072021300)}^{0.16} \qquad \text{Substitute 0.16 for x}\\ &\approx 26.35 \qquad \text{Round to the nearest hundredth} \end{align*}\]

If a \(160\)-pound person drives after having \(6\) drinks, he or she is about \(26.35\) times more likely to crash than if driving while sober.

Here is the same problem done using desmos. If "Log Mode" is not checked, desmos will provide a more accurate model that does not match the results of many other graphing utilities including those used to obtain the results in this example. You can view the problem in desmos by clicking https://www.desmos.com/calculator/ev2papvkzo.

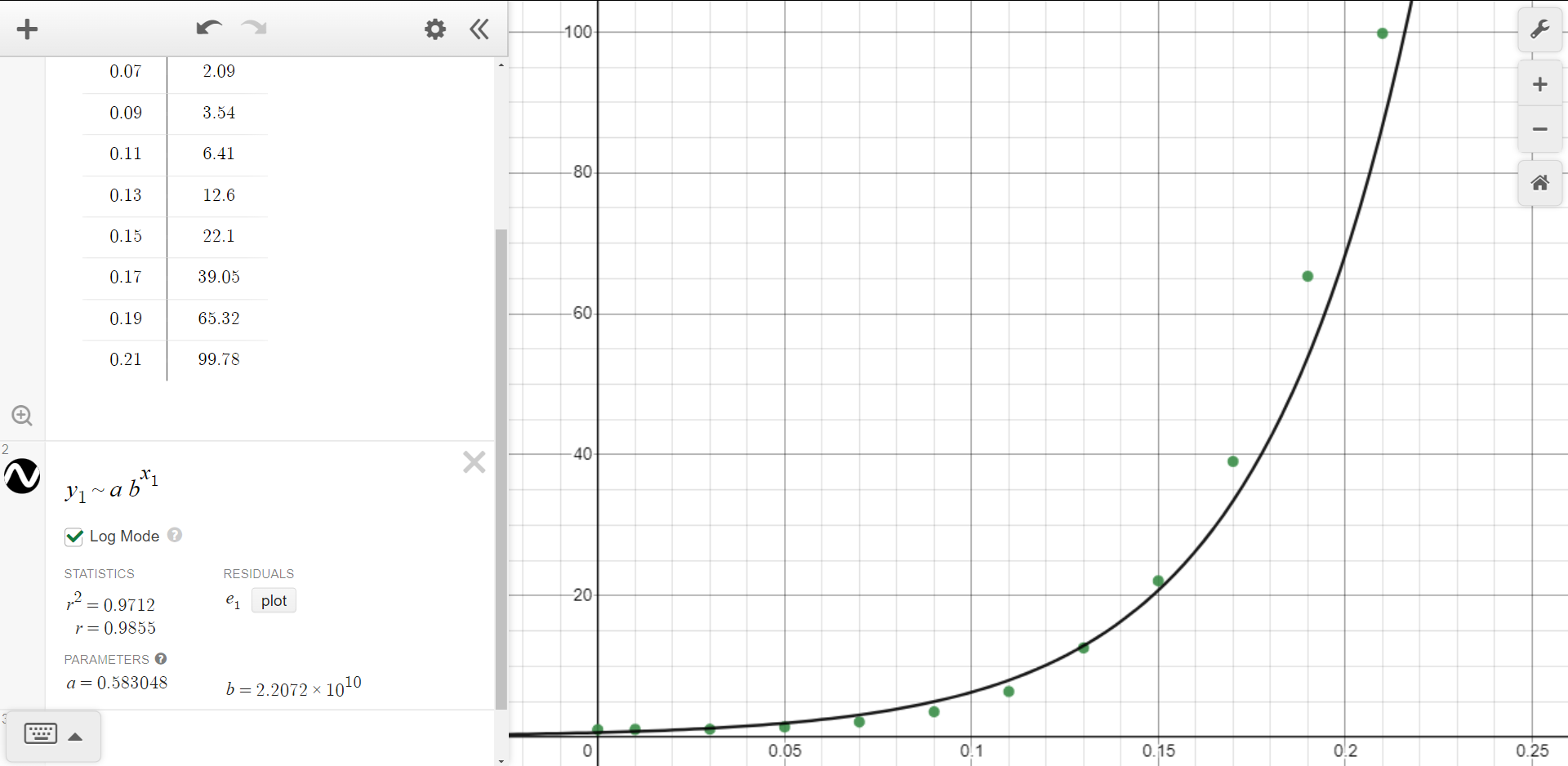
Figure \(\PageIndex{3}\)

Exercise \(\PageIndex{1}\)

Table \(\PageIndex{2}\) shows a recent graduate’s credit card balance each month after graduation.

Table \(\PageIndex{2}\)

Month	1	2	3	4	5	6	7	8
Debt ($)	620.00	761.88	899.80	1039.93	1270.63	1589.04	1851.31	2154.92

1. Use exponential regression to fit a model to these data.
2. If spending continues at this rate, what will the graduate’s credit card debt be one year after graduating?

Answer a

The exponential regression model that fits these data is \(y=522.88585984{(1.19645256)}^x\).

Answer b

If spending continues at this rate, the graduate’s credit card debt will be \($4,499.38\) after one year.

Q&A: Is it reasonable to assume that an exponential regression model will represent a situation indefinitely?

No. Remember that models are formed by real-world data gathered for regression. It is usually reasonable to make estimates within the interval of original observation (interpolation). However, when a model is used to make predictions, it is important to use reasoning skills to determine whether the model makes sense for inputs far beyond the original observation interval (extrapolation).