5.5: Applications of Exponential and Logarithmic Functions

As we mentioned in Section 6.1, exponential and logarithmic functions are used to model a wide variety of behaviors in the real world. In the examples that follow, note that while the applications are drawn from many different disciplines, the mathematics remains essentially the same. Due to the applied nature of the problems we will examine in this section, the calculator is often used to express our answers as decimal approximations.

6.5.1. Applications of Exponential Functions

Perhaps the most well-known application of exponential functions comes from the financial world. Suppose you have \(\$ 100\) to invest at your local bank and they are offering a whopping \(5 \, \%\) annual percentage interest rate. This means that after one year, the bank will pay you \(5 \%\) of that \(\$100\), or \(\$ 100(0.05) =\$ 5\) in interest, so you now have \(\$105\).¹ This is in accordance with the formula for simple interest which you have undoubtedly run across at some point before.

Equation 6.1. Simple Interest

The amount of interest \(I\) accrued at an annual rate \(r\) on an investment^a \(P\) after \(t\) years is \[I = Prt\nonumber\] The amount \(A\) in the account after \(t\) years is given by \[A = P + I = P + Prt = P(1+rt)\nonumber\]

---

^a Called the principal

Suppose, however, that six months into the year, you hear of a better deal at a rival bank.² Naturally, you withdraw your money and try to invest it at the higher rate there. Since six months is one half of a year, that initial \(\$100\) yields \(\$100(0.05)\left(\frac{1}{2}\right) = \$ 2.50\) in interest. You take your \(\$102.50\) off to the competitor and find out that those restrictions which may apply actually apply to you, and you return to your bank which happily accepts your \(\$102.50\) for the remaining six months of the year. To your surprise and delight, at the end of the year your statement reads \(\$105.06\), not \(\$105\) as you had expected.³ Where did those extra six cents come from? For the first six months of the year, interest was earned on the original principal of \(\$100\), but for the second six months, interest was earned on \(\$102.50\), that is, you earned interest on your interest. This is the basic concept behind compound interest. In the previous discussion, we would say that the interest was compounded twice, or semiannually.⁴ If more money can be earned by earning interest on interest already earned, a natural question to ask is what happens if the interest is compounded more often, say \(4\) times a year, which is every three months, or ‘quarterly.’ In this case, the money is in the account for three months, or \(\frac{1}{4}\) of a year, at a time. After the first quarter, we have \(A = P(1+rt) = \$100 \left(1 + 0.05 \cdot \frac{1}{4} \right) = \$101.25\). We now invest the \(\$101.25\) for the next three months and find that at the end of the second quarter, we have \(A = \$101.25 \left(1 + 0.05 \cdot \frac{1}{4} \right)\approx \$102.51\). Continuing in this manner, the balance at the end of the third quarter is \(\$103.79\), and, at last, we obtain \(\$105.08\). The extra two cents hardly seems worth it, but we see that we do in fact get more money the more often we compound. In order to develop a formula for this phenomenon, we need to do some abstract calculations. Suppose we wish to invest our principal \(P\) at an annual rate \(r\) and compound the interest \(n\) times per year. This means the money sits in the account \(\frac{1}{n}^{\mbox{\tiny th}}\) of a year between compoundings. Let \(A_{k}\) denote the amount in the account after the \(k^{\mbox{\tiny th}}\) compounding. Then \(A_{1} = P\left(1 + r\left(\frac{1}{n}\right)\right)\) which simplifies to \(A_{1} = P \left(1 + \frac{r}{n}\right)\). After the second compounding, we use \(A_{1}\) as our new principal and get \(A_{2} = A_{1} \left(1 + \frac{r}{n}\right) = \left[P \left(1 + \frac{r}{n}\right)\right]\left(1 + \frac{r}{n}\right) = P \left(1 + \frac{r}{n}\right)^2\). Continuing in this fashion, we get \(A_{3} =P \left(1 + \frac{r}{n}\right)^3\), \(A_{4} =P \left(1 + \frac{r}{n}\right)^4\), and so on, so that \(A_{k} = P \left(1 + \frac{r}{n}\right)^k\). Since we compound the interest \(n\) times per year, after \(t\) years, we have \(nt\) compoundings. We have just derived the general formula for compound interest below.

Equation 6.2. Compounded Interest

If an initial principal \(P\) is invested at an annual rate \(r\) and the interest is compounded \(n\) times per year, the amount \(A\) in the account after \(t\) years is \[A(t) = P \left(1 + \frac{r}{n}\right)^{nt}\nonumber\]

If we take \(P = 100\), \(r = 0.05\), and \(n = 4\), Equation 6.2 becomes \(A(t) = 100\left(1+ \frac{0.05}{4}\right)^{4t}\) which reduces to \(A(t) = 100(1.0125)^{4t}\). To check this new formula against our previous calculations, we find \(A\left(\frac{1}{4}\right) = 100(1.0125)^{4 \left(\frac{1}{4}\right)} = 101.25\), \(A\left(\frac{1}{2}\right) \approx \$102.51\), \(A\left(\frac{3}{4}\right) \approx \$103.79\), and \(A(1) \approx \$105.08\).

Example 6.5.1

Suppose \(\$2000\) is invested in an account which offers \(7.125 \%\) compounded monthly.

1. Express the amount \(A\) in the account as a function of the term of the investment \(t\) in years.
2. How much is in the account after \(5\) years?
3. How long will it take for the initial investment to double?
4. Find and interpret the average rate of change⁵ of the amount in the account from the end of the fourth year to the end of the fifth year, and from the end of the thirty-fourth year to the end of the thirty-fifth year.

Solution.

1. Substituting \(P = 2000\), \(r = 0.07125\), and \(n = 12\) (since interest is compounded monthly) into Equation 6.2 yields \(A(t) = 2000\left(1 + \frac{0.07125}{12}\right)^{12t}=2000 (1.0059375)^{12t}\).
2. Since \(t\) represents the length of the investment in years, we substitute \(t=5\) into \(A(t)\) to find \(A(5) = 2000 (1.0059375)^{12(5)} \approx 2852.92\). After \(5\) years, we have approximately \(\$2852.92\).
3. Our initial investment is \(\$2000\), so to find the time it takes this to double, we need to find \(t\) when \(A(t) = 4000\). We get \(2000 (1.0059375)^{12t}=4000\), or \((1.0059375)^{12t}=2\). Taking natural logs as in Section 6.3, we get \(t = \frac{\ln(2)}{12 \ln(1.0059375)} \approx 9.75\). Hence, it takes approximately \(9\) years \(9\) months for the investment to double.
4. To find the average rate of change of \(A\) from the end of the fourth year to the end of the fifth year, we compute \(\frac{A(5)-A(4)}{5-4} \approx 195.63\). Similarly, the average rate of change of \(A\) from the end of the thirty-fourth year to the end of the thirty-fifth year is \(\frac{A(35)-A(34)}{35-34} \approx 1648.21\). This means that the value of the investment is increasing at a rate of approximately \(\$195.63\) per year between the end of the fourth and fifth years, while that rate jumps to \(\$1648.21\) per year between the end of the thirty-fourth and thirty-fifth years. So, not only is it true that the longer you wait, the more money you have, but also the longer you wait, the faster the money increases.⁶

We have observed that the more times you compound the interest per year, the more money you will earn in a year. Let’s push this notion to the limit.⁷ Consider an investment of \(\$ 1\) invested at \(100 \%\) interest for \(1\) year compounded \(n\) times a year. Equation 6.2 tells us that the amount of money in the account after \(1\) year is \(A = \left(1+\frac{1}{n}\right)^{n}\). Below is a table of values relating \(n\) and \(A\).

\[\begin{array}{|r||r|} \hline n & A \\ \hline 1 & 2 \\ \hline 2 & 2.25 \\ \hline 4 & \approx 2.4414 \\ \hline 12 & \approx 2.6130 \\ \hline 360 & \approx 2.7145 \\ \hline 1000 & \approx 2.7169 \\ \hline 10000 & \approx 2.7181 \\ \hline 100000 & \approx 2.7182 \\ \hline \end{array}\nonumber\]

As promised, the more compoundings per year, the more money there is in the account, but we also observe that the increase in money is greatly diminishing. We are witnessing a mathematical ‘tug of war’. While we are compounding more times per year, and hence getting interest on our interest more often, the amount of time between compoundings is getting smaller and smaller, so there is less time to build up additional interest. With Calculus, we can show⁸ that as \(n \rightarrow \infty\), \(A = \left(1+\frac{1}{n}\right)^{n} \rightarrow e\), where \(e\) is the natural base first presented in Section 6.1. Taking the number of compoundings per year to infinity results in what is called continuously compounded interest.

Theorem 6.8.

If you invest \(\$1\) at \(100 \%\) interest compounded continuously, then you will have \(\$ e\) at the end of one year.

Using this definition of \(e\) and a little Calculus, we can take Equation 6.2 and produce a formula for continuously compounded interest.

Equation 6.3. Continuously Compounded Interest

If an initial principal \(P\) is invested at an annual rate \(r\) and the interest is compounded continuously, the amount \(A\) in the account after \(t\) years is \[A(t) = P e^{rt}\nonumber\]

If we take the scenario of Example 6.5.1 and compare monthly compounding to continuous compounding over \(35\) years, we find that monthly compounding yields \(A(35) = 2000 (1.0059375)^{12(35)}\) which is about \(\$ 24,\!035.28\), whereas continuously compounding gives \(A(35) = 2000e^{0.07125 (35)}\) which is about \(\$ 24,\!213.18\) - a difference of less than \(1 \%\).

Equations 6.2 and 6.3 both use exponential functions to describe the growth of an investment. Curiously enough, the same principles which govern compound interest are also used to model short term growth of populations. In Biology, The Law of Uninhibited Growth states as its premise that the instantaneous rate at which a population increases at any time is directly proportional to the population at that time.⁹ In other words, the more organisms there are at a given moment, the faster they reproduce. Formulating the law as stated results in a differential equation, which requires Calculus to solve. Its solution is stated below.

Equation 6.4. Uninhibited Growth

If a population increases according to The Law of Uninhibited Growth, the number of organisms \(N\) at time \(t\) is given by the formula \[N(t) = N_0e^{kt},\nonumber\] where \(N(0) = N_0\) (read ‘\(N\) nought’) is the initial number of organisms and \(k>0\) is the constant of proportionality which satisfies the equation

\[\left(\mbox{instantaneous rate of change of $N(t)$ at time $t$}\right) = k \, N(t)\nonumber\]

It is worth taking some time to compare Equations 6.3 and 6.4. In Equation 6.3, we use \(P\) to denote the initial investment; in Equation 6.4, we use \(N_0\) to denote the initial population. In Equation 6.3, \(r\) denotes the annual interest rate, and so it shouldn’t be too surprising that the \(k\) in Equation 6.4 corresponds to a growth rate as well. While Equations 6.3 and 6.4 look entirely different, they both represent the same mathematical concept.

Example 6.5.2

In order to perform arthrosclerosis research, epithelial cells are harvested from discarded umbilical tissue and grown in the laboratory. A technician observes that a culture of twelve thousand cells grows to five million cells in one week. Assuming that the cells follow The Law of Uninhibited Growth, find a formula for the number of cells, \(N\), in thousands, after \(t\) days.

Solution

We begin with \(N(t) = N_0e^{kt}\). Since \(N\) is to give the number of cells in thousands, we have \(N_0 = 12\), so \(N(t) = 12e^{kt}\). In order to complete the formula, we need to determine the growth rate \(k\). We know that after one week, the number of cells has grown to five million. Since \(t\) measures days and the units of \(N\) are in thousands, this translates mathematically to \(N(7) = 5000\). We get the equation \(12e^{7k} = 5000\) which gives \(k = \frac{1}{7} \ln\left(\frac{1250}{3}\right)\). Hence, \(N(t) = 12e^{ \frac{t}{7} \ln\left(\frac{1250}{3}\right)}\). Of course, in practice, we would approximate \(k\) to some desired accuracy, say \(k \approx 0.8618\), which we can interpret as an \(86.18 \%\) daily growth rate for the cells.

Whereas Equations 6.3 and 6.4 model the growth of quantities, we can use equations like them to describe the decline of quantities. One example we’ve seen already is Example 6.1.1 in Section 6.1. There, the value of a car declined from its purchase price of \(\$25,\!000\) to nothing at all. Another real world phenomenon which follows suit is radioactive decay. There are elements which are unstable and emit energy spontaneously. In doing so, the amount of the element itself diminishes. The assumption behind this model is that the rate of decay of an element at a particular time is directly proportional to the amount of the element present at that time. In other words, the more of the element there is, the faster the element decays. This is precisely the same kind of hypothesis which drives The Law of Uninhibited Growth, and as such, the equation governing radioactive decay is hauntingly similar to Equation 6.4 with the exception that the rate constant \(k\) is negative.

Equation 6.5. Radioactive Decay

The amount of a radioactive element \(A\) at time \(t\) is given by the formula \[A(t) = A_0e^{kt},\nonumber\] where \(A(0) = A_0\) is the initial amount of the element and \(k<0\) is the constant of proportionality which satisfies the equation

\[\left(\mbox{instantaneous rate of change of $A(t)$ at time $t$}\right) = k \, A(t)\nonumber\]

Example 6.5.3

Iodine-131 is a commonly used radioactive isotope used to help detect how well the thyroid is functioning. Suppose the decay of Iodine-131 follows the model given in Equation 6.5, and that the half-life¹⁰ of Iodine-131 is approximately \(8\) days. If \(5\) grams of Iodine-131 is present initially, find a function which gives the amount of Iodine-131, \(A\), in grams, \(t\) days later.

Solution

Since we start with \(5\) grams initially, Equation 6.5 gives \(A(t) = 5e^{kt}\). Since the half-life is \(8\) days, it takes \(8\) days for half of the Iodine-131 to decay, leaving half of it behind. Hence, \(A(8) = 2.5\) which means \(5e^{8k} = 2.5\). Solving, we get \(k = \frac{1}{8} \ln\left(\frac{1}{2}\right) = -\frac{\ln(2)}{8} \approx -0.08664\), which we can interpret as a loss of material at a rate of \(8.664 \%\) daily. Hence, \(A(t) = 5 e^{-\frac{t\ln(2)}{8}} \approx 5 e^{-0.08664t}\).

We now turn our attention to some more mathematically sophisticated models. One such model is Newton’s Law of Cooling, which we first encountered in Example 6.1.2 of Section 6.1. In that example we had a cup of coffee cooling from \(160^{\circ}\mbox{F}\) to room temperature \(70^{\circ}\mbox{F}\) according to the formula \(T(t) = 70 + 90 e^{-0.1 t}\), where \(t\) was measured in minutes. In this situation, we know the physical limit of the temperature of the coffee is room temperature,¹¹ and the differential equation which gives rise to our formula for \(T(t)\) takes this into account. Whereas the radioactive decay model had a rate of decay at time \(t\) directly proportional to the amount of the element which remained at time \(t\), Newton’s Law of Cooling states that the rate of cooling of the coffee at a given time \(t\) is directly proportional to how much of a temperature exists between the coffee at time \(t\) and room temperature, not the temperature of the coffee itself. In other words, the coffee cools faster when it is first served, and as its temperature nears room temperature, the coffee cools ever more slowly. Of course, if we take an item from the refrigerator and let it sit out in the kitchen, the object’s temperature will rise to room temperature, and since the physics behind warming and cooling is the same, we combine both cases in the equation below.

Equation 6.6. Newton’s Law of Cooling (Warming)

The temperature \(T\) of an object at time \(t\) is given by the formula \[T(t) = T_{a} + \left(T_0 - T_{a}\right) e^{-kt},\nonumber\] where \(T(0) = T_0\) is the initial temperature of the object, \(T_{a}\) is the ambient temperature^a and \(k>0\) is the constant of proportionality which satisfies the equation

\[\left(\mbox{instantaneous rate of change of $T(t)$ at time $t$}\right) = k \, \left(T(t) - T_{a}\right)\nonumber\]

---

^a That is, the temperature of the surroundings.

If we re-examine the situation in Example 6.1.2 with \(T_0 = 160\), \(T_{a} = 70\), and \(k = 0.1\), we get, according to Equation 6.6, \(T(t) = 70 + (160 - 70)e^{-0.1t}\) which reduces to the original formula given. The rate constant \(k = 0.1\) indicates the coffee is cooling at a rate equal to \(10 \%\) of the difference between the temperature of the coffee and its surroundings. Note in Equation 6.6 that the constant \(k\) is positive for both the cooling and warming scenarios. What determines if the function \(T(t)\) is increasing or decreasing is if \(T_0\) (the initial temperature of the object) is greater than \(T_{a}\) (the ambient temperature) or vice-versa, as we see in our next example.

Example 6.5.4.

A \(40^{\circ}\mbox{F}\) roast is cooked in a \(350^{\circ}\mbox{F}\) oven. After \(2\) hours, the temperature of the roast is \(125^{\circ}\mbox{F}\).

1. Assuming the temperature of the roast follows Newton’s Law of Warming, find a formula for the temperature of the roast \(T\) as a function of its time in the oven, \(t\), in hours.
2. The roast is done when the internal temperature reaches \(165^{\circ}\mbox{F}\). When will the roast be done?

Solution.

1. The initial temperature of the roast is \(40^{\circ}\mbox{F}\), so \(T_0 = 40\). The environment in which we are placing the roast is the \(350^{\circ}\mbox{F}\) oven, so \(T_{a} = 350\). Newton’s Law of Warming tells us \(T(t) = 350 + (40-350)e^{-kt}\), or \(T(t) = 350 - 310e^{-kt}\). To determine \(k\), we use the fact that after \(2\) hours, the roast is \(125^{\circ}\mbox{F}\), which means \(T(2) = 125\). This gives rise to the equation \(350 - 310e^{-2k} = 125\) which yields \(k = -\frac{1}{2} \ln \left( \frac{45}{62} \right) \approx 0.1602\). The temperature function is \[T(t) = 350 - 310 e^{\frac{t}{2} \ln \left( \frac{45}{62} \right)} \approx 350- 310 e^{-0.1602 t}.\nonumber\]
2. To determine when the roast is done, we set \(T(t) = 165\). This gives \(350- 310 e^{-0.1602 t} = 165\) whose solution is \(t = -\frac{1}{0.1602} \ln \left( \frac{37}{62} \right) \approx 3.22\). It takes roughly \(3\) hours and \(15\) minutes to cook the roast completely.

If we had taken the time to graph \(y=T(t)\) in Example 6.5.4, we would have found the horizontal asymptote to be \(y = 350\), which corresponds to the temperature of the oven. We can also arrive at this conclusion by applying a bit of ‘number sense’. As t \(\rightarrow \infty,-0.1602 t \approx \text { very big }(-)\) so that \(e^{-0.1602 t} \approx \text { very small }(+)\). The larger the value of \(t\), the smaller \(e^{-0.1602 t}\) becomes so that \(T(t) \approx 350-\text { very small }(+)\), which indicates the graph of \(y=T(t)\) is approaching its horizontal asymptote \(y=350\) from below. Physically, this means the roast will eventually warm up to \(350^{\circ}\mbox{F}\).¹² The function \(T\) is sometimes called a limited growth model, since the function \(T\) remains bounded as \(t \rightarrow \infty\). If we apply the principles behind Newton’s Law of Cooling to a biological example, it says the growth rate of a population is directly proportional to how much room the population has to grow. In other words, the more room for expansion, the faster the growth rate. The logistic growth model combines The Law of Uninhibited Growth with limited growth and states that the rate of growth of a population varies jointly with the population itself as well as the room the population has to grow.

Equation 6.7. Logistic Growth

If a population behaves according to the assumptions of logistic growth, the number of organisms \(N\) at time \(t\) is given by the equation \[N(t) =\dfrac{L}{1 + Ce^{-kLt}},\nonumber\] where \(N(0) = N_0\) is the initial population, \(L\) is the limiting population,^a \(C\) is a measure of how much room there is to grow given by \[C = \dfrac{L}{N_0} - 1.\nonumber\] and \(k > 0\) is the constant of proportionality which satisfies the equation

\[\left(\mbox{instantaneous rate of change of $N(t)$ at time $t$}\right) = k \, N(t) \left(L - N(t)\right)\nonumber\]

---

^a That is, a \(t \rightarrow \infty, N(t) \rightarrow L\)

The logistic function is used not only to model the growth of organisms, but is also often used to model the spread of disease and rumors.¹³

Example 6.5.5

The number of people \(N\), in hundreds, at a local community college who have heard the rumor ‘Carl is afraid of Virginia Woolf’ can be modeled using the logistic equation

\[N(t) = \dfrac{84}{1+2799e^{-t}},\nonumber\]

where \(t\geq 0\) is the number of days after April 1, 2009.

1. Find and interpret \(N(0)\).
2. Find and interpret the end behavior of \(N(t)\).
3. How long until \(4200\) people have heard the rumor?
4. Check your answers to 2 and 3 using your calculator.

Solution.

1. We find \(N(0) = \frac{84}{1+2799e^{0}} = \frac{84}{2800} = \frac{3}{100}\). Since \(N(t)\) measures the number of people who have heard the rumor in hundreds, \(N(0)\) corresponds to \(3\) people. Since \(t=0\) corresponds to April 1, 2009, we may conclude that on that day, \(3\) people have heard the rumor.¹⁴
2. We could simply note that \(N(t)\) is written in the form of Equation 6.7, and identify \(L = 84\). However, to see why the answer is \(84\), we proceed analytically. Since the domain of \(N\) is restricted to \(t \geq 0\), the only end behavior of significance is \(t \rightarrow \infty\). As we’ve seen before,¹⁵ as \(t \rightarrow \infty\), we have \(1997 e^{-t} \rightarrow 0^{+}\) and so \(N(t) \approx \frac{84}{1+\text { very small }(+)} \approx 84\). Hence, as \(t \rightarrow \infty\), \(N(t) \rightarrow 84\). This means that as time goes by, the number of people who will have heard the rumor approaches \(8400\).
3. To find how long it takes until \(4200\) people have heard the rumor, we set \(N(t) = 42\). Solving \(\frac{84}{1+2799e^{-t}} = 42\) gives \(t = \ln(2799) \approx 7.937\). It takes around \(8\) days until \(4200\) people have heard the rumor.
4. We graph \(y=N(x)\) using the calculator and see that the line \(y=84\) is the horizontal asymptote of the graph, confirming our answer to part 2, and the graph intersects the line \(y=42\) at \(x = \ln(2799) \approx 7.937\), which confirms our answer to part 3.

   

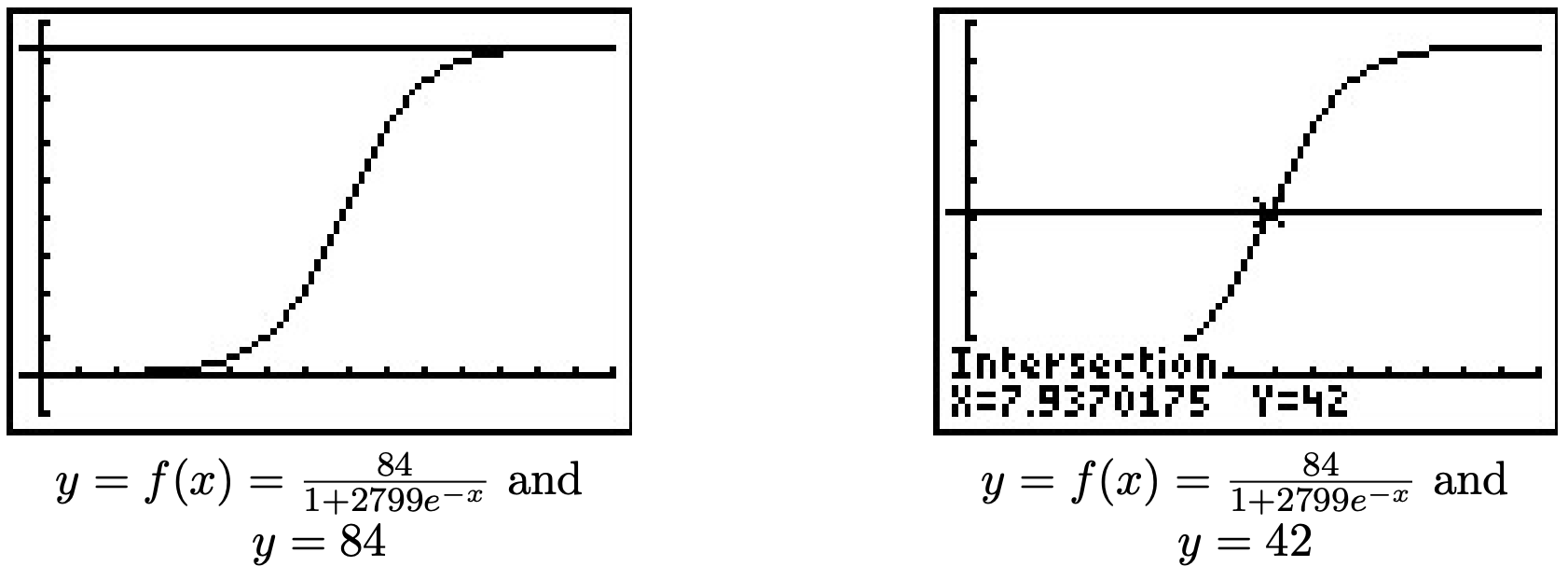
If we take the time to analyze the graph of \(y=N(x)\) above, we can see graphically how logistic growth combines features of uninhibited and limited growth. The curve seems to rise steeply, then at some point, begins to level off. The point at which this happens is called an inflection point or is sometimes called the ‘point of diminishing returns’. At this point, even though the function is still increasing, the rate at which it does so begins to decline. It turns out the point of diminishing returns always occurs at half the limiting population. (In our case, when \(y=42\).) While these concepts are more precisely quantified using Calculus, below are two views of the graph of \(y=N(x)\), one on the interval \([0,8]\), the other on \([8,15]\). The former looks strikingly like uninhibited growth; the latter like limited growth.

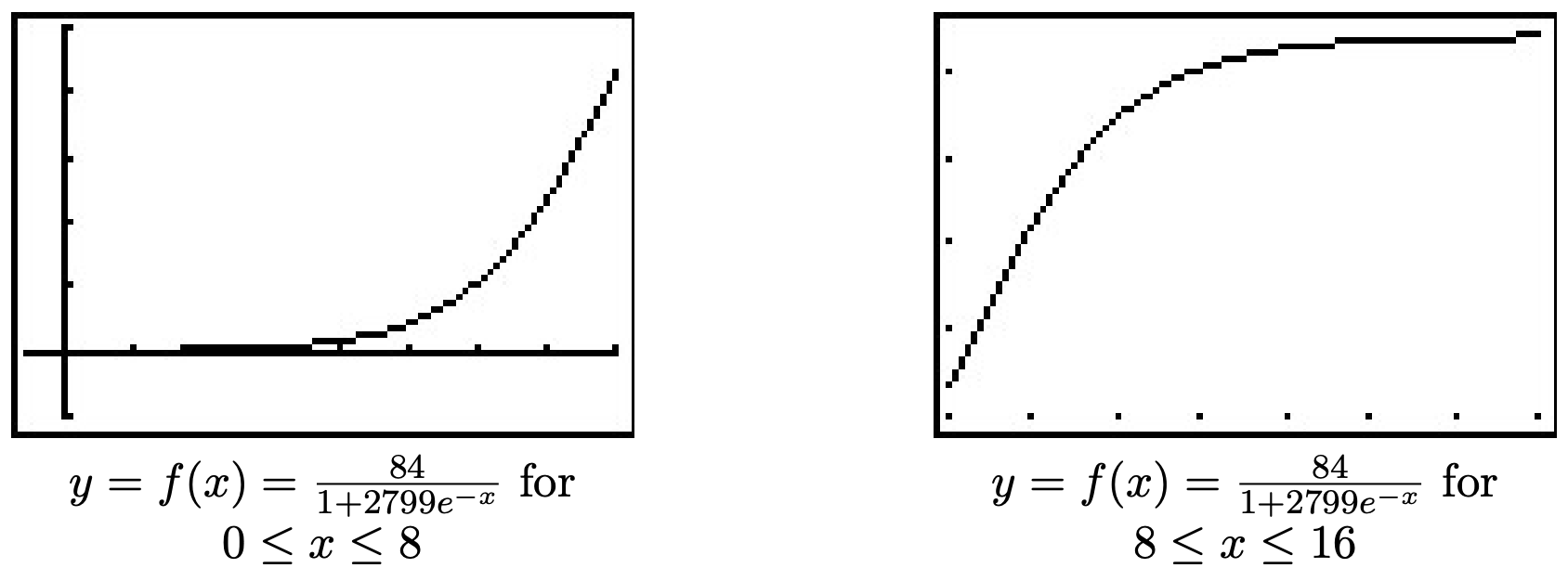
6.5.2 Applications of Logarithms

Just as many physical phenomena can be modeled by exponential functions, the same is true of logarithmic functions. In Exercises 75, 76 and 77 of Section 6.1, we showed that logarithms are useful in measuring the intensities of earthquakes (the Richter scale), sound (decibels) and acids and bases (pH). We now present yet a different use of the a basic logarithm function, password strength.

Example 6.5.6

The information entropy \(H\), in bits, of a randomly generated password consisting of \(L\) characters is given by \(H = L \log_{2}(N)\), where \(N\) is the number of possible symbols for each character in the password. In general, the higher the entropy, the stronger the password.

1. If a \(7\) character case-sensitive¹⁶ password is comprised of letters and numbers only, find the associated information entropy.
2. How many possible symbol options per character is required to produce a \(7\) character password with an information entropy of \(50\) bits?

Solution.

1. There are \(26\) letters in the alphabet, \(52\) if upper and lower case letters are counted as different. There are \(10\) digits (\(0\) through \(9\)) for a total of \(N=62\) symbols. Since the password is to be \(7\) characters long, \(L = 7\). Thus, \(H = 7 \log_{2}(62) = \frac{7 \ln(62)}{\ln(2)} \approx 41.68\).
2. We have \(L = 7\) and \(H=50\) and we need to find \(N\). Solving the equation \(50 = 7 \log_{2}(N)\) gives \(N = 2^{50/7} \approx 141.323\), so we would need \(142\) different symbols to choose from.¹⁷

Chemical systems known as buffer solutions have the ability to adjust to small changes in acidity to maintain a range of pH values. Buffer solutions have a wide variety of applications from maintaining a healthy fish tank to regulating the pH levels in blood. Our next example shows how the pH in a buffer solution is a little more complicated than the pH we first encountered in Exercise 77 in Section 6.1.

Example 6.5.7

Blood is a buffer solution. When carbon dioxide is absorbed into the bloodstream it produces carbonic acid and lowers the pH. The body compensates by producing bicarbonate, a weak base to partially neutralize the acid. The equation¹⁸ which models blood pH in this situation is \(\mbox{pH} = 6.1 + \log\left(\frac{800}{x} \right)\), where \(x\) is the partial pressure of carbon dioxide in arterial blood, measured in torr. Find the partial pressure of carbon dioxide in arterial blood if the pH is \(7.4\).

Solution

We set \(\mbox{pH} = 7.4\) and get \(7.4 = 6.1 + \log\left(\frac{800}{x} \right)\), or \(\log\left(\frac{800}{x} \right) = 1.3\). Solving, we find \(x = \frac{800}{10^{1.3}} \approx 40.09\). Hence, the partial pressure of carbon dioxide in the blood is about \(40\) torr.

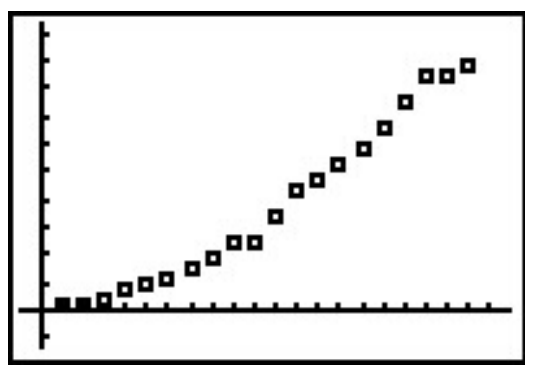
Another place logarithms are used is in data analysis. Suppose, for instance, we wish to model the spread of influenza A (H1N1), the so-called ‘Swine Flu’. Below is data taken from the World Health Organization (WHO) where \(t\) represents the number of days since April 28, 2009, and \(N\) represents the number of confirmed cases of H1N1 virus worldwide.

\[\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline t & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \\ \hline N & 148 & 257 & 367 & 658 & 898 & 1085 & 1490 & 1893 & 2371 & 2500 & 3440 & 4379 & 4694 \\ \hline \end{array}\nonumber\]

\[\begin{array}{|c||c||c|c|c|c|c|c|} \hline t & 14 & 15 & 16 & 17 & 18 & 19& 20 \\ \hline N & 5251 & 5728 & 6497 & 7520 & 8451 & 8480 & 8829 \\ \hline \end{array}\nonumber\]

Making a scatter plot of the data treating \(t\) as the independent variable and \(N\) as the dependent variable gives

Which models are suggested by the shape of the data? Thinking back Section 2.5, we try a Quadratic Regression, with pretty good results.

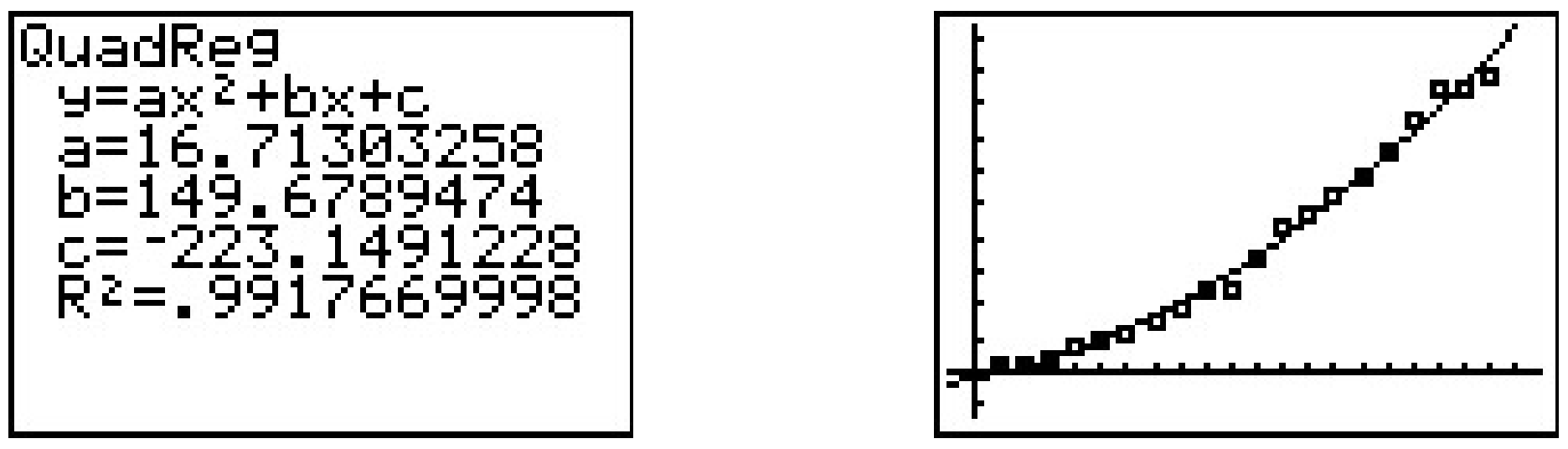
However, is there any scientific reason for the data to be quadratic? Are there other models which fit the data equally well, or better? Scientists often use logarithms in an attempt to ‘linearize’ data sets - in other words, transform the data sets to produce ones which result in straight lines. To see how this could work, suppose we guessed the relationship between \(N\) and \(t\) was some kind of power function, not necessarily quadratic, say \(N = B t^{A}\). To try to determine the \(A\) and \(B\), we can take the natural log of both sides and get \(\ln(N) = \ln\left(B t^{A}\right)\). Using properties of logs to expand the right hand side of this equation, we get \(\ln(N) = A \ln(t) + \ln(B)\). If we set \(X = \ln(t)\) and \(Y = \ln(N)\), this equation becomes \(Y = AX + \ln(B)\). In other words, we have a line with slope \(A\) and \(Y\)-intercept \(\ln(B)\). So, instead of plotting \(N\) versus \(t\), we plot \(\ln(N)\) versus \(\ln(t)\).

\[\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \ln(t) & 0 & 0.693 & 1.099 & 1.386& 1.609 & 1.792 & 1.946 & 2.079 & 2.197 & 2.302 & 2.398 & 2.485 & 2.565 \\ \hline \ln(N) & 4.997 & 5.549 & 5.905 & 6.489 & 6.800 & 6.989 & 7.306 & 7.546 & 7.771 & 7.824 & 8.143 & 8.385 & 8.454 \\ \hline \end{array}\nonumber\]

\[\begin{array}{|c||c||c|c|c|c|c|c|} \hline \ln(t) & 2.639 & 2.708 & 2.773 & 2.833 & 2.890 & 2.944 & 2.996 \\ \hline \ln(N) & 8.566 & 8.653 & 8.779 & 8.925 & 9.042 & 9.045 & 9.086 \\ \hline \end{array}\nonumber\]

Running a linear regression on the data gives

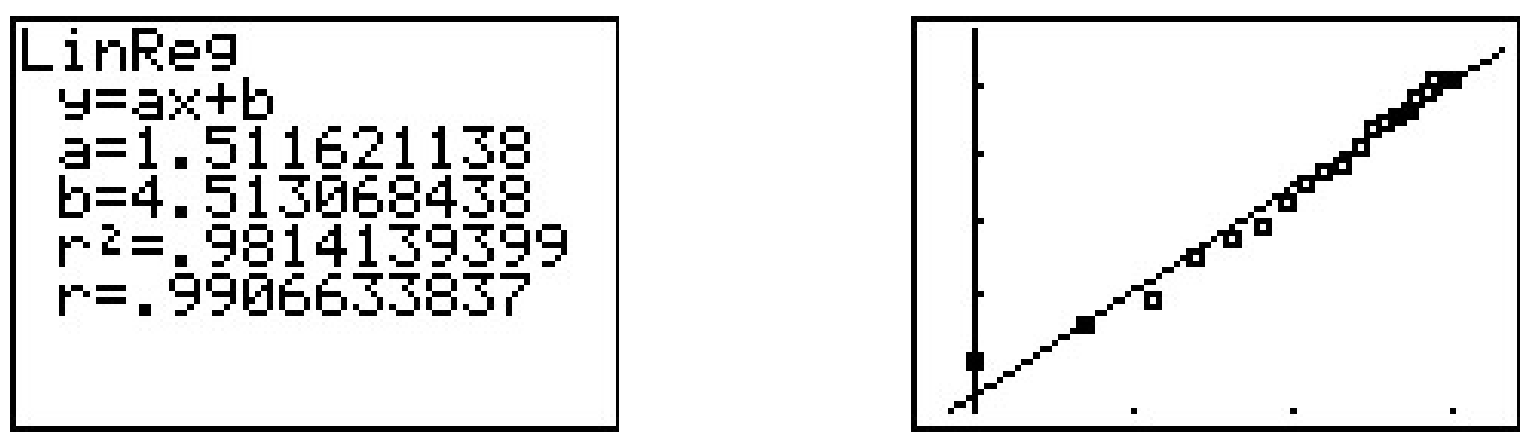
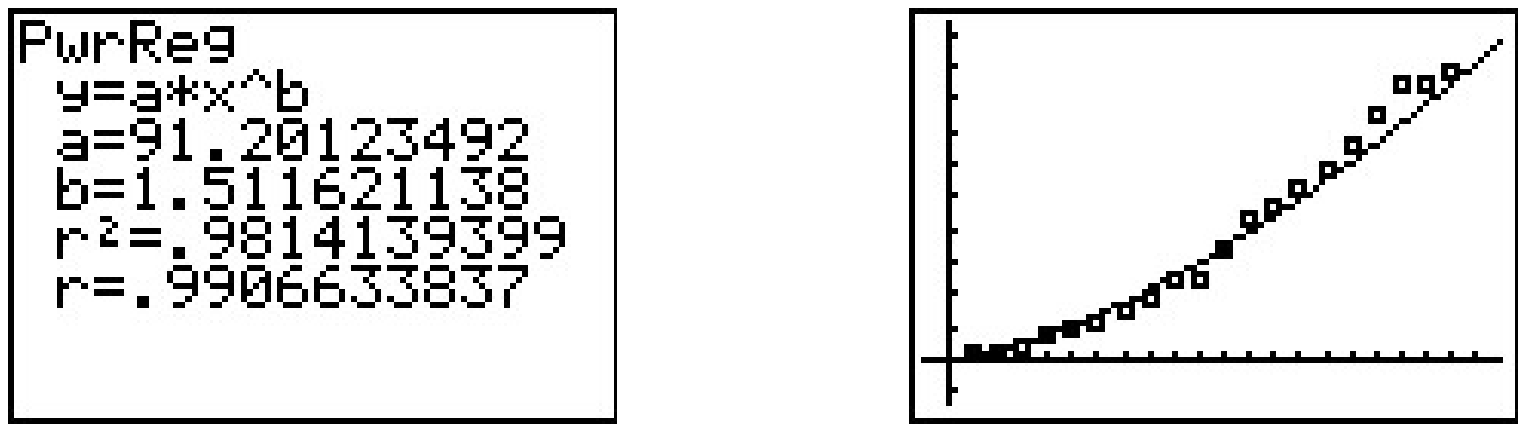
The slope of the regression line is \(a \approx 1.512\) which corresponds to our exponent \(A\). The \(y\)-intercept \(b \approx 4.513\) corresponds to \(\ln(B)\), so that \(B \approx 91.201\). Hence, we get the model \(N = 91.201 t^{1.512}\), something from Section 5.3. Of course, the calculator has a built-in ‘Power Regression’ feature. If we apply this to our original data set, we get the same model we arrived at before.¹⁹

This is all well and good, but the quadratic model appears to fit the data better, and we’ve yet to mention any scientific principle which would lead us to believe the actual spread of the flu follows any kind of power function at all. If we are to attack this data from a scientific perspective, it does seem to make sense that, at least in the early stages of the outbreak, the more people who have the flu, the faster it will spread, which leads us to proposing an uninhibited growth model. If we assume \(N = B e^{At}\) then, taking logs as before, we get \(\ln(N) = At + \ln(B)\). If we set \(X = t\) and \(Y = \ln(N)\), then, once again, we get \(Y = AX + \ln(B)\), a line with slope \(A\) and \(Y\)-intercept \(\ln(B)\). Plotting \(\ln(N)\) versus \(t\) gives the following linear regression.

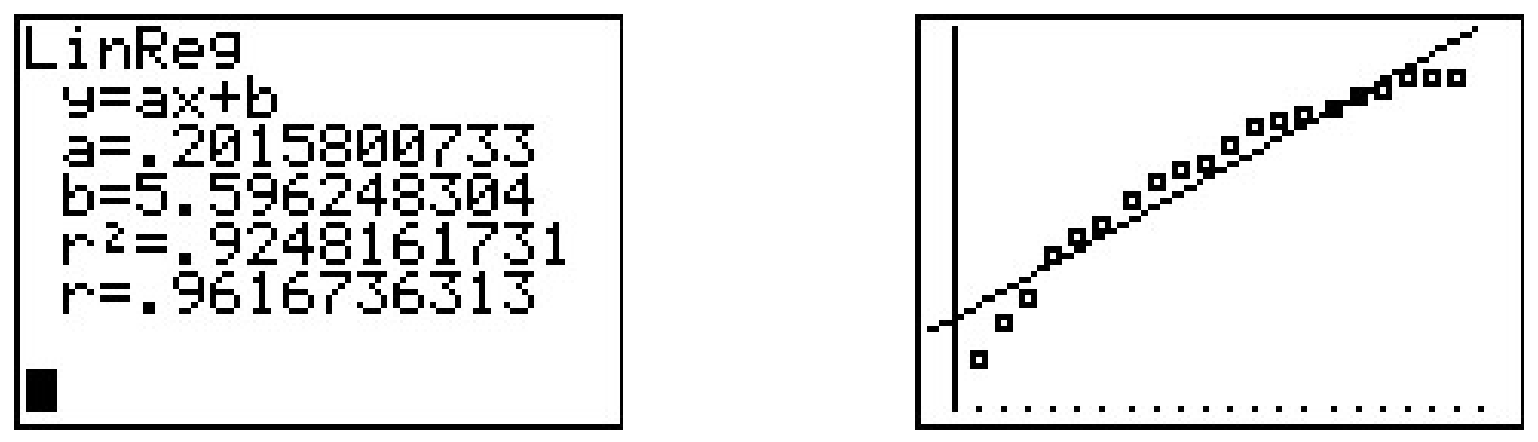
We see the slope is \(a \approx 0.202\) and which corresponds to \(A\) in our model, and the \(y\)-intercept is \(b \approx 5.596\) which corresponds to \(\ln(B)\). We get \(B \approx 269.414\), so that our model is \(N = 269.414e^{0.202t}\). Of course, the calculator has a built-in ‘Exponential Regression’ feature which produces what appears to be a different model \(N = 269.414 (1.22333419)^{t}\). Using properties of exponents, we write \(e^{0.202t} = \left(e^{0.202}\right)^t \approx (1.223848)^{t}\), which, had we carried more decimal places, would have matched the base of the calculator model exactly.

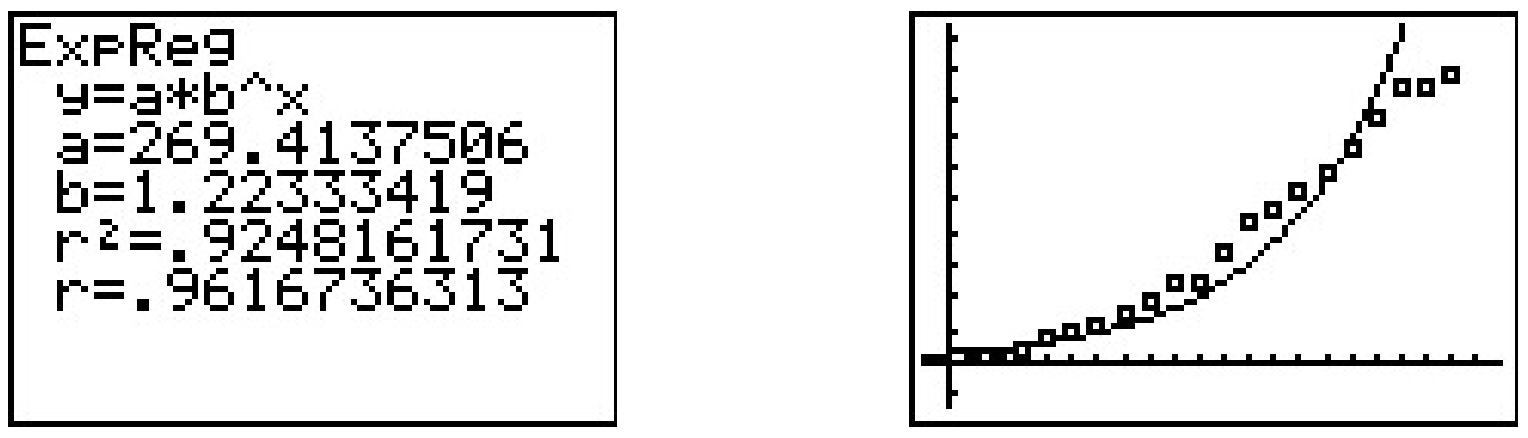
The exponential model didn’t fit the data as well as the quadratic or power function model, but it stands to reason that, perhaps, the spread of the flu is not unlike that of the spread of a rumor and that a logistic model can be used to model the data. The calculator does have a ‘Logistic Regression’ feature, and using it produces the model \(N = \frac{10739.147}{1 + 42.416 e^{0.268 t}}\).

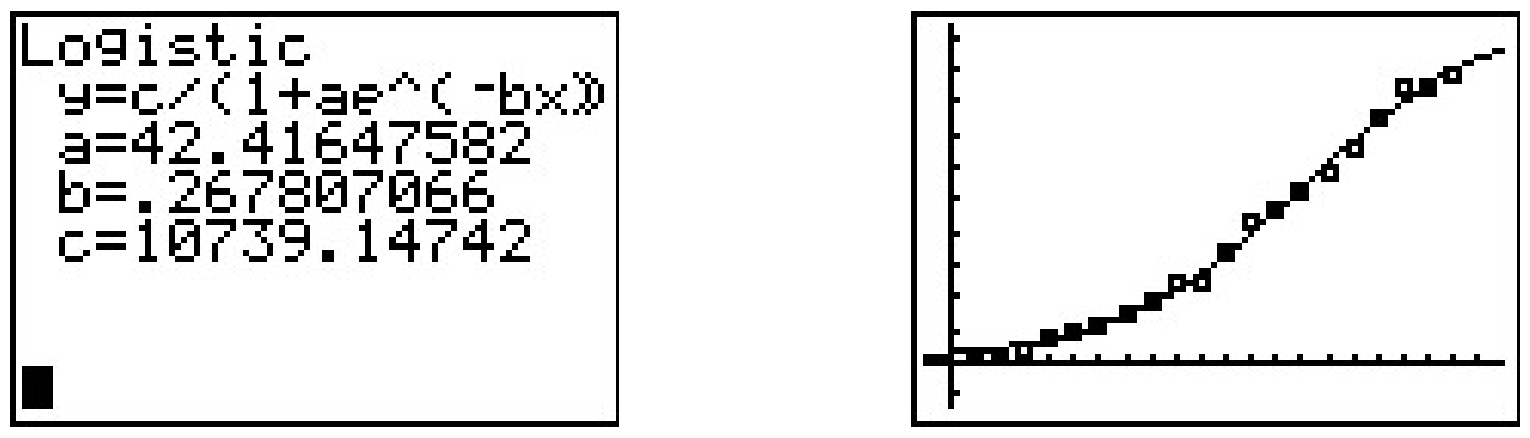
This appears to be an excellent fit, but there is no friendly coefficient of determination, \(R^2\), by which to judge this numerically. There are good reasons for this, but they are far beyond the scope of the text. Which of the models, quadratic, power, exponential, or logistic is the ‘best model’? If by ‘best’ we mean ‘fits closest to the data,’ then the quadratic and logistic models are arguably the winners with the power function model a close second. However, if we think about the science behind the spread of the flu, the logistic model gets an edge. For one thing, it takes into account that only a finite number of people will ever get the flu (according to our model, \(10,\!739\)), whereas the quadratic model predicts no limit to the number of cases. As we have stated several times before in the text, mathematical models, regardless of their sophistication, are just that: models, and they all have their limitations.²⁰

6.5.3. Exercises

For each of the scenarios given in Exercises 1 - 6,

• Find the amount \(A\) in the account as a function of the term of the investment \(t\) in years.
• Determine how much is in the account after \(5\) years, \(10\) years, \(30\) years and \(35\) years. Round your answers to the nearest cent.
• Determine how long will it take for the initial investment to double. Round your answer to the nearest year.
• Find and interpret the average rate of change of the amount in the account from the end of the fourth year to the end of the fifth year, and from the end of the thirty-fourth year to the end of the thirty-fifth year. Round your answer to two decimal places.

1. \(\$500\) is invested in an account which offers \(0.75 \%\), compounded monthly.
2. \(\$500\) is invested in an account which offers \(0.75 \%\), compounded continuously.
3. \(\$1000\) is invested in an account which offers \(1.25 \%\), compounded monthly.
4. \(\$1000\) is invested in an account which offers \(1.25 \%\), compounded continuously.
5. \(\$5000\) is invested in an account which offers \(2.125 \%\), compounded monthly.
6. \(\$5000\) is invested in an account which offers \(2.125 \%\), compounded continuously.
7. Look back at your answers to Exercises 1 - 6. What can be said about the difference between monthly compounding and continuously compounding the interest in those situations? With the help of your classmates, discuss scenarios where the difference between monthly and continuously compounded interest would be more dramatic. Try varying the interest rate, the term of the investment and the principal. Use computations to support your answer.
8. How much money needs to be invested now to obtain \(\$2000\) in 3 years if the interest rate in a savings account is \(0.25 \%\), compounded continuously? Round your answer to the nearest cent.
9. How much money needs to be invested now to obtain \(\$5000\) in 10 years if the interest rate in a CD is \(2.25 \%\), compounded monthly? Round your answer to the nearest cent.
10. On May, 31, 2009, the Annual Percentage Rate listed at Jeff’s bank for regular savings accounts was \(0.25\%\) compounded monthly. Use Equation 6.2 to answer the following.
    1. If \(P = 2000\) what is \(A(8)\)?
    2. Solve the equation \(A(t) = 4000\) for \(t\).
    3. What principal \(P\) should be invested so that the account balance is $2000 is three years?
11. Jeff’s bank also offers a 36-month Certificate of Deposit (CD) with an APR of \(2.25\%\).
    1. If \(P = 2000\) what is \(A(8)\)?
    2. Solve the equation \(A(t) = 4000\) for \(t\).
    3. What principal \(P\) should be invested so that the account balance is $2000 in three years?
    4. The Annual Percentage Yield is the interest rate that returns the same amount of interest after one year as the compound interest does. With the help of your classmates, compute the APY for this investment.
12. A finance company offers a promotion on \(\$5000\) loans. The borrower does not have to make any payments for the first three years, however interest will continue to be charged to the loan at \(29.9 \%\) compounded continuously. What amount will be due at the end of the three year period, assuming no payments are made? If the promotion is extended an additional three years, and no payments are made, what amount would be due?
13. Use Equation 6.2 to show that the time it takes for an investment to double in value does depend on the principal \(P\), but rather, depends only on the APR and the number of compoundings per year. Let \(n = 12\) and with the help of your classmates compute the doubling time for a variety of rates \(r\). Then look up the Rule of 72 and compare your answers to what that rule says. If you’re really interested²¹ in Financial Mathematics, you could also compare and contrast the Rule of 72 with the Rule of 70 and the Rule of 69.

In Exercises 14 - 18, we list some radioactive isotopes and their associated half-lives. Assume that each decays according to the formula \(A(t)=A_{0} e^{k t}\) where \(A_{0}\) is the initial amount of the material and \(k\) is the decay constant. For each isotope:

• Find the decay constant \(k\). Round your answer to four decimal places.
• Find a function which gives the amount of isotope \(A\) which remains after time \(t\). (Keep the units of \(A\) and \(t\) the same as the given data.)
• Determine how long it takes for \(90 \%\) of the material to decay. Round your answer to two decimal places. (HINT: If \(90 \%\) of the material decays, how much is left?)

14. Cobalt 60, used in food irradiation, initial amount 50 grams, half-life of \(5.27\) years.
15. Phosphorus 32, used in agriculture, initial amount 2 milligrams, half-life \(14\) days.
16. Chromium 51, used to track red blood cells, initial amount 75 milligrams, half-life \(27.7\) days.
17. Americium 241, used in smoke detectors, initial amount 0.29 micrograms, half-life \(432.7\) years.
18. Uranium 235, used for nuclear power, initial amount \(1\) kg grams, half-life \(704\) million years.
19. With the help of your classmates, show that the time it takes for \(90 \%\) of each isotope listed in Exercises 14 - 18 to decay does not depend on the initial amount of the substance, but rather, on only the decay constant \(k\). Find a formula, in terms of \(k\) only, to determine how long it takes for \(90 \%\) of a radioactive isotope to decay.
20. In Example 6.1.1 in Section 6.1, the exponential function \(V(x) = 25 \left(\frac{4}{5}\right)^{x}\) was used to model the value of a car over time. Use the properties of logs and/or exponents to rewrite the model in the form \(V(t) = 25e^{kt}\).
21. The Gross Domestic Product (GDP) of the US (in billions of dollars) \(t\) years after the year 2000 can be modeled by: \[G(t) = 9743.77 e^{0.0514t}\nonumber\]
    1. Find and interpret \(G(0)\).
    2. According to the model, what should have been the GDP in 2007? In 2010? (According to the US Department of Commerce, the 2007 GDP was \(\$14,369.1\) billion and the 2010 GDP was \(\$14,657.8\) billion.)
22. The diameter \(D\) of a tumor, in millimeters, \(t\) days after it is detected is given by: \[D(t) = 15e^{0.0277t}\nonumber\]
    1. What was the diameter of the tumor when it was originally detected?
    2. How long until the diameter of the tumor doubles?
23. Under optimal conditions, the growth of a certain strain of E. Coli is modeled by the Law of Uninhibited Growth \(N(t)=N_{0} e^{k t}\) where \(N_{0}\) is the initial number of bacteria and \(t\) is the elapsed time, measured in minutes. From numerous experiments, it has been determined that the doubling time of this organism is 20 minutes. Suppose 1000 bacteria are present initially.
    1. Find the growth constant \(k\). Round your answer to four decimal places.
    2. Find a function which gives the number of bacteria \(N(t)\) after \(t\) minutes.
    3. How long until there are 9000 bacteria? Round your answer to the nearest minute.
24. Yeast is often used in biological experiments. A research technician estimates that a sample of yeast suspension contains 2.5 million organisms per cubic centimeter (cc). Two hours later, she estimates the population density to be 6 million organisms per cc. Let \(t\) be the time elapsed since the first observation, measured in hours. Assume that the yeast growth follows the Law of Uninhibited Growth \(N(t)=N_{0} e^{k t}\).
    1. Find the growth constant \(k\). Round your answer to four decimal places.
    2. Find a function which gives the number of yeast (in millions) per cc \(N(t)\) after \(t\) hours.
    3. What is the doubling time for this strain of yeast?
25. The Law of Uninhibited Growth also applies to situations where an animal is re-introduced into a suitable environment. Such a case is the reintroduction of wolves to Yellowstone National Park. According to the National Park Service, the wolf population in Yellowstone National Park was 52 in 1996 and 118 in 1999. Using these data, find a function of the form \(N(t)=N_{0} e^{k t}\) which models the number of wolves \(t\) years after 1996. (Use \(t = 0\) to represent the year 1996. Also, round your value of \(k\) to four decimal places.) According to the model, how many wolves were in Yellowstone in 2002? (The recorded number is 272.)
26. During the early years of a community, it is not uncommon for the population to grow according to the Law of Uninhibited Growth. According to the Painesville Wikipedia entry, in 1860, the Village of Painesville had a population of 2649. In 1920, the population was 7272. Use these two data points to fit a model of the form \(N(t)=N_{0} e^{k t}\) were \(N(t)\) is the number of Painesville Residents \(t\) years after 1860. (Use \(t = 0\) to represent the year 1860. Also, round the value of \(k\) to four decimal places.) According to this model, what was the population of Painesville in 2010? (The 2010 census gave the population as 19,563) What could be some causes for such a vast discrepancy? For more on this, see Exercise 37.
27. The population of Sasquatch in Bigfoot county is modeled by \[P(t) = \dfrac{120}{1 + 3.167e^{-0.05t}}\nonumber\] where \(P(t)\) is the population of Sasquatch \(t\) years after \(2010\).
    1. Find and interpret \(P(0)\).
    2. Find the population of Sasquatch in Bigfoot county in 2013. Round your answer to the nearest Sasquatch.
    3. When will the population of Sasquatch in Bigfoot county reach 60? Round your answer to the nearest year.
    4. Find and interpret the end behavior of the graph of \(y = P(t)\). Check your answer using a graphing utility.
28. The half-life of the radioactive isotope Carbon-14 is about 5730 years.
    1. Use Equation 6.5 to express the amount of Carbon-14 left from an initial \(N\) milligrams as a function of time \(t\) in years.
    2. What percentage of the original amount of Carbon-14 is left after 20,000 years?
    3. If an old wooden tool is found in a cave and the amount of Carbon-14 present in it is estimated to be only 42% of the original amount, approximately how old is the tool?
    4. Radiocarbon dating is not as easy as these exercises might lead you to believe. With the help of your classmates, research radiocarbon dating and discuss why our model is somewhat over-simplified.
29. Carbon-14 cannot be used to date inorganic material such as rocks, but there are many other methods of radiometric dating which estimate the age of rocks. One of them, Rubidium-Strontium dating, uses Rubidium-87 which decays to Strontium-87 with a half-life of 50 billion years. Use Equation 6.5 to express the amount of Rubidium-87 left from an initial 2.3 micrograms as a function of time \(t\) in billions of years. Research this and other radiometric techniques and discuss the margins of error for various methods with your classmates.
30. Use Equation 6.5 to show that \(k = -\dfrac{\ln(2)}{h}\) where \(h\) is the half-life of the radioactive isotope.
31. A pork roast²² was taken out of a hardwood smoker when its internal temperature had reached \(180^{\circ}\)F and it was allowed to rest in a \(75^{\circ}\)F house for 20 minutes after which its internal temperature had dropped to \(170^{\circ}\)F. Assuming that the temperature of the roast follows Newton’s Law of Cooling (Equation 6.6),
    1. Express the temperature \(T\) (in \(^{\circ}\)F) as a function of time \(t\) (in minutes).
    2. Find the time at which the roast would have dropped to \(140^{\circ}\)F had it not been carved and eaten.
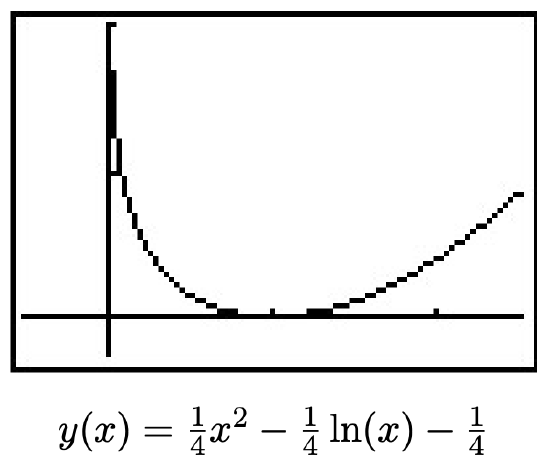
32. In reference to Exercise 44 in Section 5.3, if Fritzy the Fox’s speed is the same as Chewbacca the Bunny’s speed, Fritzy’s pursuit curve is given by

    \[y(x) = \frac{1}{4} x^2-\frac{1}{4} \ln(x)-\frac{1}{4}\nonumber\]

    Use your calculator to graph this path for \(x > 0\). Describe the behavior of \(y\) as \(x \rightarrow 0^{+}\) and interpret this physically.

33. The current \(i\) measured in amps in a certain electronic circuit with a constant impressed voltage of 120 volts is given by \(i(t) = 2 - 2e^{-10t}\) where \(t \geq 0\) is the number of seconds after the circuit is switched on. Determine the value of \(i\) as \(t \rightarrow \infty\). (This is called the steady state current.)
34. If the voltage in the circuit in Exercise 33 above is switched off after 30 seconds, the current is given by the piecewise-defined function

    \[i(t) = \left\{ \begin{array}{rcl} 2 - 2e^{-10t} & \mbox{if} & 0 \leq t < 30 \\ [6pt] \left(2 - 2e^{-300}\right) e^{-10t+300} & \mbox{if} & t \geq 30 \end{array} \right.\nonumber\]

    With the help of your calculator, graph \(y = i(t)\) and discuss with your classmates the physical significance of the two parts of the graph \(0 \leq t < 30\) and \(t \geq 30\).

35. In Exercise 6a in Section 2.5, we stated that the cable of a suspension bridge formed a parabola but that a free hanging cable did not. A free hanging cable forms a and its basic shape is given by \(y = \frac{1}{2}\left(e^{x} + e^{-x}\right)\). Use your calculator to graph this function. What are its domain and range? What is its end behavior? Is it invertible? How do you think it is related to the function given in Exercise 47 in Section 6.3 and the one given in the answer to Exercise 38 in Section 6.4? When flipped upside down, the catenary makes an arch. The Gateway Arch in St. Louis, Missouri has the shape \[y = 757.7 - \frac{127.7}{2}\left(e^{\frac{x}{127.7}} + e^{-\frac{x}{127.7}}\right)\nonumber\] where \(x\) and \(y\) are measured in feet and \(-315 \leq x \leq 315\). Find the highest point on the arch.
36. In Exercise 6a in Section 2.5, we examined the data set given below which showed how two cats and their surviving offspring can produce over 80 million cats in just ten years. It is virtually impossible to see this data plotted on your calculator, so plot \(x\) versus \(\ln(x)\) as was done on page 480. Find a linear model for this new data and comment on its goodness of fit. Find an exponential model for the original data and comment on its goodness of fit.

    \(\begin{array}{|l|r|r|r|r|r|r|r|r|r|r|}
    \hline \text { Year } x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & & 9 \\
    \hline \text { Number of } & & & & & & & & & & \\
    \text { Cats } N(x) & 12 & 66 & 382 & 2201 & 12680 & 73041 & 420715 & 2423316 & 13968290 & 80399780 \\
    \hline
    \end{array}\)

37. This exercise is a follow-up to Exercise 26 which more thoroughly explores the population growth of Painesville, Ohio. According to Wikipedia, the population of Painesville, Ohio is given by \[\begin{aligned}
    &\begin{array}{|l|r|r|r|r|r|r|r|r|r|r|}
    \hline \text { Year } t & 1860 & 1870 & 1880 & 1890 & 1900 & 1910 & 1920 & 1930 & 1940 & 1950 \\
    \hline \text { Population } & 2649 & 3728 & 3841 & 4755 & 5024 & 5501 & 7272 & 10944 & 12235 & 14432 \\
    \hline
    \end{array}\\
    &\begin{array}{|l|r|r|r|r|r|}
    \hline \text { Year } t & 1960 & 1970 & 1980 & 1990 & 2000 \\
    \hline \text { Population } & 16116 & 16536 & 16351 & 15699 & 17503 \\
    \hline
    \end{array}
    \end{aligned}\nonumber\]
    1. Use a graphing utility to perform an exponential regression on the data from 1860 through 1920 only, letting \(t = 0\) represent the year 1860 as before. How does this calculator model compare with the model you found in Exercise 26? Use the calculator’s exponential model to predict the population in 2010. (The 2010 census gave the population as 19,563)
    2. The logistic model fit to all of the given data points for the population of Painesville \(t\) years after 1860 (again, using \(t = 0\) as 1860) is \[P(t) = \dfrac{18691}{1+9.8505e^{-0.03617t}}\nonumber\] According to this model, what should the population of Painesville have been in 2010? (The 2010 census gave the population as 19,563.) What is the population limit of Painesville?
38. According to OhioBiz , the census data for Lake County, Ohio is as follows: \[\begin{aligned}
    &\begin{array}{|l|r|r|r|r|r|r|r|r|r|r|}
    \hline \text { Year } t & 1860 & 1870 & 1880 & 1890 & 1900 & 1910 & 1920 & 1930 & 1940 & 1950 \\
    \hline \text { Population } & 15576 & 15935 & 16326 & 18235 & 21680 & 22927 & 28667 & 41674 & 50020 & 75979 \\
    \hline
    \end{array}\\
    &\begin{array}{|l|r|r|r|r|r|}
    \hline \text { Year } t & 1960 & 1970 & 1980 & 1990 & 2000 \\
    \hline \text { Population } & 148700 & 197200 & 212801 & 215499 & 227511 \\
    \hline
    \end{array}
    \end{aligned}\nonumber\]
    1. Use your calculator to fit a logistic model to these data, using \(x = 0\) to represent the year 1860.
    2. Graph these data and your logistic function on your calculator to judge the reasonableness of the fit.
    3. Use this model to estimate the population of Lake County in 2010. (The 2010 census gave the population to be 230,041.)
    4. According to your model, what is the population limit of Lake County, Ohio?
39. According to facebook , the number of active users of facebook has grown significantly since its initial launch from a Harvard dorm room in February 2004. The chart below has the approximate number \(U(x)\) of active users, in , \(x\) months after February 2004. For example, the first entry \((10, 1)\) means that there were \(1\) million active users in December 2004 and the last entry \((77, 500)\) means that there were \(500\) million active users in July 2010.

    With the help of your classmates, find a model for this data.

40. Each Monday during the registration period before the Fall Semester at LCCC, the Enrollment Planning Council gets a report prepared by the data analysts in Institutional Effectiveness and Planning.²³ While the ongoing enrollment data is analyzed in many different ways, we shall focus only on the overall headcount. Below is a chart of the enrollment data for Fall Semester 2008. It starts 21 weeks before “Opening Day” and ends on “Day 15” of the semester, but we have relabeled the top row to be \(x = 1\) through \(x = 24\) so that the math is easier. (Thus, \(x = 22\) is Opening Day.) \[\begin{aligned}
    &\begin{array}{|l|r|r|r|r|r|r|r|r|}
    \hline \text { Week } x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
    \hline \text { Total } & & & & & & & & \\
    \text { Headcount } & 1194 & 1564 & 2001 & 2475 & 2802 & 3141 & 3527 & 3790 \\
    \hline
    \end{array}\\
    &\begin{array}{|l|r|r|r|r|r|r|r|r|}
    \hline \text { Week } x & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\
    \hline \text { Total } & & & & & & & & \\
    \text { Headcount } & 4065 & 4371 & 4611 & 4945 & 5300 & 5657 & 6056 & 6478 \\
    \hline
    \end{array}
    \end{aligned}\nonumber\] \[\begin{array}{|l|r|r|r|r|r|r|r|r|}
    \hline \text { Week } x & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 \\
    \hline \text { Total } & & & & & & & & \\
    \text { Headcount } & 7161 & 7772 & 8505 & 9256 & 10201 & 10743 & 11102 & 11181 \\
    \hline
    \end{array}\nonumber\]

    With the help of your classmates, find a model for this data. Unlike most of the phenomena we have studied in this section, there is no single differential equation which governs the enrollment growth. Thus there is no scientific reason to rely on a logistic function even though the data plot may lead us to that model. What are some factors which influence enrollment at a community college and how can you take those into account mathematically?

41. When we wrote this exercise, the Enrollment Planning Report for Fall Semester 2009 had only 10 data points for the first 10 weeks of the registration period. Those numbers are given below. \[\begin{array}{|l|r|r|r|r|r|r|r|r|}
    \hline \text { Week } x & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 \\
    \hline \text { Total } & & & & & & & & \\
    \text { Headcount } & 7161 & 7772 & 8505 & 9256 & 10201 & 10743 & 11102 & 11181 \\
    \hline
    \end{array}\nonumber\]

    With the help of your classmates, find a model for this data and make a prediction for the Opening Day enrollment as well as the Day 15 enrollment. (WARNING: The registration period for 2009 was one week shorter than it was in 2008 so Opening Day would be \(x = 21\) and Day 15 is \(x = 23\).)

6.5.4. Answers

1. • \(A(t) = 500\left(1 + \frac{0.0075}{12}\right)^{12t}\)
   • \(A(5) \approx \$ 519.10\), \(A(10) \approx \$ 538.93\), \(A(30) \approx \$ 626.12\), \(A(35) \approx \$ 650.03\)
   • It will take approximately \(92\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(3.88\). This means that the investment is growing at an average rate of \(\$3.88\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(4.85\). This means that the investment is growing at an average rate of \(\$4.85\) per year at this point.
2. • \(A(t) = 500e^{0.0075t}\)
   • \(A(5) \approx \$ 519.11\), \(A(10) \approx \$ 538.94\), \(A(30) \approx \$ 626.16\), \(A(35) \approx \$ 650.09\)
   • It will take approximately \(92\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(3.88\). This means that the investment is growing at an average rate of \(\$3.88\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(4.86\). This means that the investment is growing at an average rate of \(\$4.86\) per year at this point.
3. • \(A(t) = 1000\left(1 + \frac{0.0125}{12}\right)^{12t}\)
   • \(A(5) \approx \$ 1064.46\), \(A(10) \approx \$ 1133.07\), \(A(30) \approx \$ 1454.71\), \(A(35) \approx \$ 1548.48\)
   • It will take approximately \(55\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(13.22\). This means that the investment is growing at an average rate of \(\$13.22\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(19.23\). This means that the investment is growing at an average rate of \(\$19.23\) per year at this point.
4. • \(A(t) = 1000e^{0.0125t}\)
   • \(A(5) \approx \$ 1064.49\), \(A(10) \approx \$ 1133.15\), \(A(30) \approx \$ 1454.99\), \(A(35) \approx \$ 1548.83\)
   • It will take approximately \(55\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(13.22\). This means that the investment is growing at an average rate of \(\$13.22\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(19.24\). This means that the investment is growing at an average rate of \(\$19.24\) per year at this point.
5. • \(A(t) = 5000\left(1 + \frac{0.02125}{12}\right)^{12t}\)
   • \(A(5) \approx \$ 5559.98\), \(A(10) \approx \$ 6182.67\), \(A(30) \approx \$ 9453.40\), \(A(35) \approx \$ 10512.13\)
   • It will take approximately \(33\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(116.80\). This means that the investment is growing at an average rate of \(\$116.80\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(220.83\). This means that the investment is growing at an average rate of \(\$220.83\) per year at this point.
6. • \(A(t) = 5000e^{0.02125t}\)
   • \(A(5) \approx \$ 5560.50\), \(A(10) \approx \$ 6183.83\), \(A(30) \approx \$ 9458.73\), \(A(35) \approx \$ 10519.05\)
   • It will take approximately \(33\) years for the investment to double.
   • The average rate of change from the end of the fourth year to the end of the fifth year is approximately \(116.91\). This means that the investment is growing at an average rate of \(\$116.91\) per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately \(221.17\). This means that the investment is growing at an average rate of \(\$221.17\) per year at this point.

8. \(P = \frac{2000}{e^{0.0025 \cdot 3}} \approx \$ 1985.06\)
9. \(P = \frac{5000}{\left(1 + \frac{0.0225}{12}\right)^{12 \cdot 10}} \approx \$ 3993.42\)
10. 1. \(A(8) = 2000\left(1 + \frac{0.0025}{12}\right)^{12 \cdot 8} \approx \$2040.40\)
    2. \(t = \dfrac{\ln(2)}{12 \ln\left(1 + \frac{0.0025}{12}\right)} \approx 277.29\) years
    3. \(P = \dfrac{2000}{\left(1 + \frac{0.0025}{12}\right)^{36}} \approx \$1985.06\)
11. 1. \(A(8) = 2000\left(1 + \frac{0.0225}{12}\right)^{12 \cdot 8} \approx \$2394.03\)
    2. \(t = \dfrac{\ln(2)}{12 \ln\left(1 + \frac{0.0225}{12}\right)} \approx 30.83\) years
    3. \(P = \dfrac{2000}{\left(1 + \frac{0.0225}{12}\right)^{36}} \approx \$1869.57\)
    4. \(\left(1 + \frac{0.0225}{12}\right)^{12} \approx 1.0227\) so the APY is 2.27%
12. \(A(3) = 5000e^{0.299 \cdot 3} \approx \$12,226.18\), \(A(6) = 5000e^{0.299 \cdot 6} \approx \$30,067.29\)

14. • \(k = \frac{\ln(1/2)}{5.27} \approx -0.1315\)
    • \(A(t) = 50e^{-0.1315t}\)
    • \(t = \frac{\ln(0.1)}{-0.1315} \approx 17.51\) years.
15. • \(k = \frac{\ln(1/2)}{14} \approx -0.0495\)
    • \(A(t) = 2e^{-0.0495t}\)
    • \(t = \frac{\ln(0.1)}{-0.0495} \approx 46.52\) days.
16. • \(k = \frac{\ln(1/2)}{27.7} \approx -0.0250\)
    • \(A(t) = 75e^{-0.0250t}\)
    • \(t = \frac{\ln(0.1)}{-0.025} \approx 92.10\) days.
17. • \(k = \frac{\ln(1/2)}{432.7} \approx -0.0016\)
    • \(A(t) = 0.29e^{-0.0016t}\)
    • \(t = \frac{\ln(0.1)}{-0.0016} \approx 1439.11\) years.
18. • \(k = \frac{\ln(1/2)}{704} \approx -0.0010\)
    • \(A(t) = e^{-0.0010t}\)
    • \(t = \frac{\ln(0.1)}{-0.0010} \approx 2302.58\) million years, or \(2.30\) billion years.
19. \(t = \frac{\ln(0.1)}{k} = -\frac{\ln(10)}{k}\)
20. \(V(t) = 25e^{\ln\left(\frac{4}{5}\right)t} \approx 25e^{-0.22314355t}\)
21. 1. \(G(0) = 9743.77\) This means that the GDP of the US in 2000 was \(\$9743.77\) billion dollars.
    2. \(G(7) = 13963.24\) and \(G(10) = 16291.25\), so the model predicted a GDP of \(\$ 13,963.24\) billion in 2007 and \(\$ 16,291.25\) billion in 2010.
22. 1. \(D(0) = 15\), so the tumor was 15 millimeters in diameter when it was first detected.
    2. \(t = \frac{\ln(2)}{0.0277} \approx 25\) days.
23. 1. \(k = \frac{\ln(2)}{20} \approx 0.0346\)
    2. \(N(t) = 1000e^{0.0346 t}\)
    3. \(t = \frac{\ln(9)}{0.0346} \approx 63\) minutes
24. 1. \(k = \frac{1}{2}\frac{\ln(6)}{2.5} \approx 0.4377\)
    2. \(N(t) = 2.5e^{0.4377 t}\)
    3. \(t = \frac{\ln(2)}{0.4377} \approx 1.58\) hours
25. \(N_{0}=52, k=\frac{1}{3} \ln \left(\frac{118}{52}\right) \approx 0.2731, N(t)=52 e^{0.2731 t} \cdot N(6) \approx 268\).
26. \(N_{0}=2649, k=\frac{1}{60} \ln \left(\frac{7272}{2649}\right) \approx 0.0168, N(t)=2649 e^{0.0168 t} \cdot N(150) \approx 32923\), so the population of Painesville in 2010 based on this model would have been 32,923.
27. 1. \(P(0) = \frac{120}{4.167} \approx 29\). There are 29 Sasquatch in Bigfoot County in 2010.
    2. \(P(3) = \frac{120}{1+3.167e^{-0.05(3)}} \approx 32\) Sasquatch.
    3. \(t = 20 \ln(3.167) \approx 23\) years.
    4. As \(t \rightarrow \infty\), \(P(t) \rightarrow 120\). As time goes by, the Sasquatch Population in Bigfoot County will approach 120. Graphically, \(y = P(x)\) has a horizontal asymptote \(y=120\).
28. 1. \(A(t) = Ne^{-\left(\frac{\ln(2)}{5730}\right)t} \approx Ne^{-0.00012097t}\)
    2. \(A(20000) \approx 0.088978 \cdot N\) so about 8.9% remains
    3. \(t \approx \dfrac{\ln(.42)}{-0.00012097} \approx 7171\) years old
29. \(A(t) = 2.3e^{-0.0138629t}\)

31. 1. \(T(t) = 75 + 105e^{-0.005005t}\)
    2. The roast would have cooled to \(140^{\circ}\)F in about 95 minutes.
32. From the graph, it appears that as \(x \rightarrow 0^{+}\), \(y \rightarrow \infty\). This is due to the presence of the \(\ln(x)\) term in the function. This means that Fritzy will never catch Chewbacca, which makes sense since Chewbacca has a head start and Fritzy only runs as fast as he does.

    

33. The steady state current is 2 amps.

36. The linear regression on the data below is \(y = 1.74899x + 0.70739\) with \(r^{2} \approx 0.999995\). This is an excellent fit. \[\begin{array}{|l|r|r|r|r|r|r|r|r|r|r|}
    \hline x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
    \hline \ln (N(x)) & 2.4849 & 4.1897 & 5.9454 & 7.6967 & 9.4478 & 11.1988 & 12.9497 & 14.7006 & 16.4523 & 18.2025 \\
    \hline
    \end{array}\nonumber\]

    \(N(x) = 2.02869(5.74879)^{x} = 2.02869e^{1.74899x}\) with \(r^{2} \approx 0.999995\). This is also an excellent fit and corresponds to our linearized model because \(\ln(2.02869) \approx 0.70739\).

37. 1. The calculator gives: \(y = 2895.06 (1.0147)^{x}\). Graphing this along with our answer from Exercise 26 over the interval \([0,60]\) shows that they are pretty close. From this model, \(y(150) \approx 25840\) which once again overshoots the actual data value.
    2. \(P(150) \approx 18717\), so this model predicts 17,914 people in Painesville in 2010, a more conservative number than was recorded in the 2010 census. As \(t \rightarrow \infty\), \(P(t) \rightarrow 18691\). So the limiting population of Painesville based on this model is 18,691 people.
38. 1. \(y = \dfrac{242526}{1+874.62e^{-0.07113x}}\), where \(x\) is the number of years since 1860.
    2. The plot of the data and the curve is below.

       

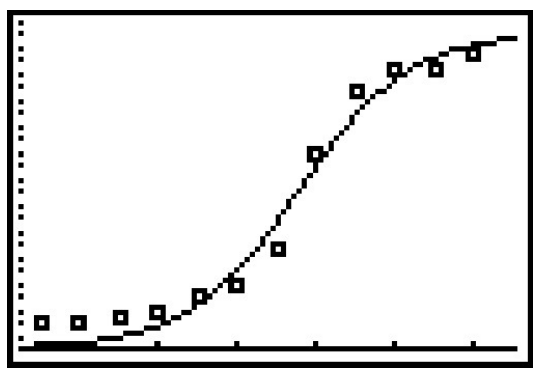
    3. \(y(140) \approx 232889\), so this model predicts 232,889 people in Lake County in 2010.
    4. As \(x \rightarrow \infty\), \(y \rightarrow 242526\), so the limiting population of Lake County based on this model is 242,526 people.

---

Reference

¹ How generous of the

² Some restrictions may apply.

³ Actually, the final balance should be $105.0625.

⁴ Using this convention, simple interest after one year is the same as compounding the interest only once.

⁵ See Definition 2.3 in section 2.1.

⁶ In fact, the rate of increase of the amount in the account is exponential as well. This is the quality that really defines exponential functions and we refer the reader to a course in Calculus.

⁷ Once you’ve had a semester of Calculus, you’ll be able to fully appreciate this very lame pun.

⁸ Or define, depending on your point of view.

⁹ The average rate of change of a function over an interval was first introduced in Section 2.1. Instantaneous rates of change are the business of Calculus, as is mentioned on Page 161.

¹⁰ The time it takes for half of the substance to decay.

¹¹ The Second Law of Thermodynamics states that heat can spontaneously flow from a hotter object to a colder one, but not the other way around. Thus, the coffee could not continue to release heat into the air so as to cool below room temperature.

¹² at which point it would be more toast than roast.

¹³ Which can be just as damaging as diseases.

¹⁴ Or, more likely, three people started the rumor. I’d wager Jeff, Jamie, and Jason started it. So much for telling your best friends something in confidence!

¹⁵ See, for example, Example 6.1.2.

¹⁶ That is, upper and lower case letters are treated as different characters.

¹⁷ Since there are only 94 distinct ASCII keyboard characters, to achieve this strength, the number of characters in the password should be increase.

¹⁸ Derived from the Henderson-Hasselbalch Equation. See Exercise 43 in Section 6.2. Hasselbalch himself was studying carbon dioxide dissolving in blood - a process called metabolic acidosis.

¹⁹ Critics may question why the authors of the book have chosen to even discuss linearization of data when the calculator has a Power Regression built-in and ready to go. Our response: talk to your science faculty

²⁰ Speaking of limitations, as of June 3, 2009, there were 19,273 confirmed cases of influenza A (H1N1). This is well above our prediction of 10,739. Each time a new report is issued, the data set increases and the model must be recalculated. We leave this recalculation to the reader.

²¹ Awesome pun!

²² This roast was enjoyed by Jeff and his family on June 10, 2009. This is real data, folks!

²³ The authors thank Dr. Wendy Marley and her staff for this data and Dr. Marcia Ballinger for the permission to use it in this problem.