1.4: Solving Right Triangles

Last updated
Save as PDF

Page ID: 61221

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Solve right triangles.
Find the area of any triangle using trigonometry.
Solve real-world problems using right triangles.
Find the measure of an angle using inverse trig functions.

Inverse Trigonometric Ratios

In mathematics, the word inverse means “undo.” For example, addition and subtraction are inverses of each other because one undoes the other. When we use the inverse trigonometric ratios, we can find acute angle measures as long as we are given two sides.

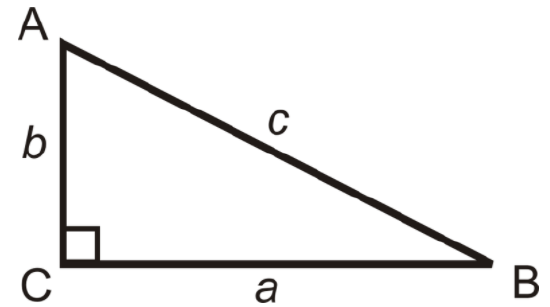
f-d_2a337f0fc303f5ead45b9c00ac0b99fc56d2875b59312a4bb58a17d7+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{1}$

Inverse Tangent: Labeled $\tan ^{-1}$, the “-1” means inverse.

$\tan ^{-1} \left(\dfrac{b}{a}\right)=m\angle B$ and $\tan ^{-1} \left(\dfrac{a}{b}\right)=m\angle A.$

Inverse Sine: Labeled $\sin ^{-1}$.

$\sin ^{-1} \left(\dfrac{b}{c}\right)=m\angle B$ and $\sin ^{-1} \left(\dfrac{a}{c}\right)=m\angle A.$

Inverse Cosine: Labeled $\cos ^{-1}$.

$\cos ^{-1} \left(\dfrac{a}{c}\right)=m\angle B$ and $\cos ^{-1} \left(\dfrac{b}{c}\right)=m\angle A.$

In most problems, to find the measure of the angles you will need to use your calculator. On most scientific and graphing calculators, the buttons look like $[\sin ^{-1}]$, $[\cos ^{-1}]$, and $[\(\tan ^{-1}]$. You might also have to hit a shift or 2nd button to access these functions.

Now that you know both the trig ratios and the inverse trig ratios you can solve a right triangle. To solve a right triangle, you need to find all sides and angles in it. You will usually use sine, cosine, or tangent; inverse sine, inverse cosine, or inverse tangent; or the Pythagorean Theorem.

What if you were told the tangent of $\angle Z$ is 0.6494? How could you find the measure of $\angle Z$?

Example $\PageIndex{1}$

Solve the right triangle.

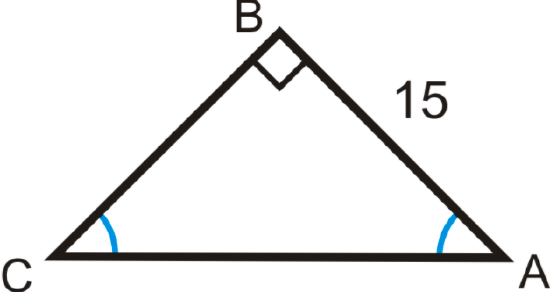$Screen Shot 2021-04-16 at 13.28.47.png$ Figure $\PageIndex{2}$

Solution

The two acute angles are congruent, making them both $45^{\circ}$. This is a 45-45-90 triangle. You can use the trigonometric ratios or the special right triangle ratios.

Trigonometric Ratios

$\begin{array}{rlrl}
\tan 45^{\circ} & =\dfrac{15}{B C} & \sin 45^{\circ} & =\dfrac{15}{A C} \\
B C & =\dfrac{15}{\tan 45^{\circ}}=15 & A C & =\dfrac{15}{\sin 45^{\circ}} \approx 21.21
\end{array}$

45-45-90 Triangle Ratios

$BC=AB=15 \text{, } AC=15\sqrt{2} \approx 21.21$

Example $\PageIndex{2}$

Use the sides of the triangle and your calculator to find the value of $\angle A$. Round your answer to the nearest tenth of a degree.

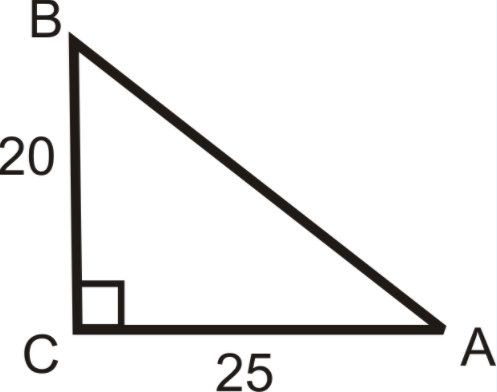$Screen Shot 2021-04-16 at 15.09.57.png$ Figure $\PageIndex{3}$

Solution

In reference to $\angle A$, we are given the opposite leg and the adjacent leg. This means we should use the tangent ratio.

$\tan A=\dfrac{20}{25}=\dfrac{4}{5}$. So, $\tan ^{-1} \dfrac{4}{5}=m\angle A$. Now, use your calculator.

If you are using a TI-83 or 84, the keystrokes would be: [2nd][TAN]($\dfrac{4}{5}$) [ENTER] and the screen looks like:

$Screen Shot 2021-04-16 at 15.10.24.png$
Figure $\PageIndex{4}$

$m\angle A \approx 38.7^{\circ}$

Example $\PageIndex{3}$

\angle A is an acute angle in a right triangle. Find $m\angle A$ to the nearest tenth of a degree for $\sin A=0.68$, $\cos A=0.85$, and $\tan A=0.34$.

Solution

$\begin{aligned} m\angle A&=\sin ^{-1} 0.68\approx 42.8^{\circ} \\ m\angle A&=\cos ^{-1} 0.85\approx 31.8^{\circ} \\ m\angle A&=\tan ^{-1} 0.34\approx 18.8^{\circ} \end{aligned}$

Example $\PageIndex{4}$

Solve the right triangle.

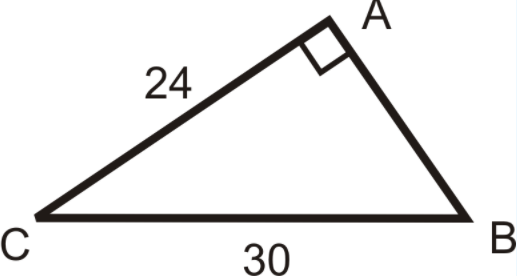
$Screen Shot 2021-04-16 at 15.10.50.png$

Figure $\PageIndex{5}$

Solution

To solve this right triangle, we need to find $AB$, $m\angle C$ and $m\angle B$. Use only the values you are given.

\(\underline{AB}: \text{ Use the Pythagorean Theorem.}

$\begin{aligned} 24^2+AB^2&=30^2 \\ 576+AB^2&=900 \\ AB^2&=324 \\ AB&=\sqrt{324}=18 \end{aligned}$

$\underline{m\angle B} : \text{ Use the inverse sine ratio.}$

$\begin{aligned} \sin B &=\dfrac{24}{30}=\dfrac{4}{5} \\ \sin ^{-1} (45) &\approx 53.1^{\circ} =m\angle B\end{aligned}$

$\underline{m\angle C} : \text{ Use the inverse cosine ratio.}$

$\cos C=\dfrac{24}{30}=\dfrac{4}{5} \rightarrow \cos ^{-1} (\dfrac{4}{5})\approx 36.9^{\circ} =m\angle C$

Example $\PageIndex{5}$

When would you use sin and when would you use $\sin ^{-1}$ ?

Solution

You would use sin when you are given an angle and you are solving for a missing side. You would use $\sin ^{-1} $when you are given sides and you are solving for a missing angle.

Review

Solving the following right triangles. Find all missing sides and angles. Round any decimal answers to the nearest tenth.

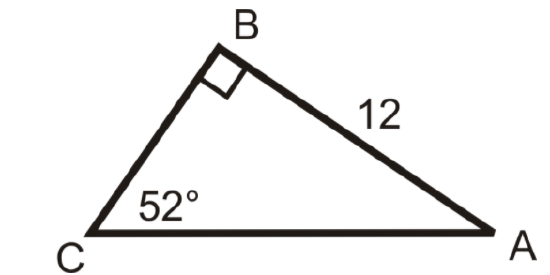
Screen Shot 2021-04-16 at 15.16.26.png — Figure $\PageIndex{6}$

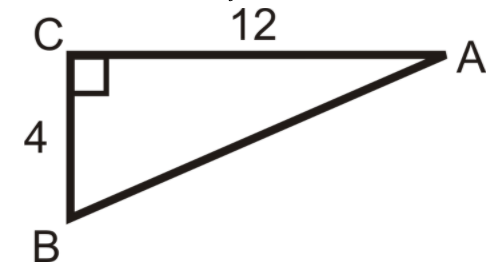
Screen Shot 2021-04-16 at 15.16.49.png — Figure $\PageIndex{7}$

Additional Resources

Interactive Element

Video: Introduction to Inverse Trigonometric Functions

Activities: Inverse Trigonometric Ratios Discussion Questions

Study Aids: Trigonometric Ratios Study Guide

Practice: Solve Right Triangles

Angles of Elevation and Depression

You can use right triangles to find distances, if you know an angle of elevation or an angle of depression.

The figure below shows each of these kinds of angles.

The angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object. For example, if you are standing on the ground looking up at the top of a mountain, you could measure the angle of elevation. The angle of depression is the angle between the horizontal line of sight and the line of sight down to an object. For example, if you were standing on top of a hill or a building, looking down at an object, you could measure the angle of depression. You can measure these angles using a clinometer or a theodolite. People tend to use clinometers or theodolites to measure the height of trees and other tall objects. Here we will solve several problems involving these angles and distances.

Finding the angle of elevation

You are standing 20 feet away from a tree, and you measure the angle of elevation to be $38^{\circ}$. How tall is the tree?

The solution depends on your height, as you measure the angle of elevation from your line of sight. Assume that you are 5 feet tall.

The figure shows us that once we find the value of $T$, we have to add 5 feet to this value to find the total height of the triangle. To find $T$, we should use the tangent value:

$\begin{aligned} tan38^{\circ}&=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{T}{20} \\ tan38^{\circ}&=\dfrac{T}{20}\\ T&=20tan38^{\circ}\approx 15.63\\ \text{Height of tree}&\approx 20.63 \text{ ft}\end{aligned}$

You are standing on top of a building, looking at a park in the distance. The angle of depression is 53^{\circ} . If the building you are standing on is 100 feet tall, how far away is the park? Does your height matter?

Finding the angle of depression

If we ignore the height of the person, we solve the following triangle:

Given the angle of depression is $53^{\circ}$, $\angle A$ in the figure above is $37^{\circ}$. We can use the tangent function to find the distance from the building to the park:

$\begin{aligned} tan 37^{\circ}=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{d}{100}\\ tan37^{\circ} &=\dfrac{d}{100}\\d&=100 tan37^{\circ} \approx 75.36\text{ ft} \end{aligned}$

If we take into account the height if the person, this will change the value of the adjacent side. For example, if the person is 5 feet tall, we have a different triangle:

$\begin{aligned} tan37^{\circ}=&\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{d}{105} \\ tan37^{\circ} &=\dfrac{d}{105} \\ d&=105 tan37^{\circ} \approx 79.12\text{ ft}\end{aligned}$

If you are only looking to estimate a distance, then you can ignore the height of the person taking the measurements. However, the height of the person will matter more in situations where the distances or lengths involved are smaller. For example, the height of the person will influence the result more in the tree height problem than in the building problem, as the tree is closer in height to the person than the building is.

Real-World Application: The Horizon

You are on a long trip through the desert. In the distance you can see mountains, and a quick measurement tells you that the angle between the mountaintop and the ground is $13.4^{\circ}$. From your studies, you know that one way to define a mountain is as a pile of land having a height of at least 2,500 meters. If you assume the mountain is the minimum possible height, how far are you away from the center of the mountain?

$\begin{aligned} tan 13.4^{\circ}&=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{2500}{d}\\ tan 13.4^{\circ} &=\dfrac{2500}{d} \\ d&=\dfrac{2500}{tan13.4^{\circ}} \approx 10,494 meters \end{aligned}$

Example $\PageIndex{6}$

You are six feet tall and measure the angle between the horizontal and a bird in the sky to be 40^{\circ} . You can see that the shadow of the bird is directly beneath the bird, and 200 feet away from you on the ground. How high is the bird in the sky?

Solution

We can use the tangent function to find out how high the bird is in the sky:

$\begin{aligned} tan40^{\circ} =\dfrac{height}{200} \\ height&=200 tan40^{\circ} \\ height&=(200)(.839) \\height&=167.8\end{aligned}$

We then need to add your height to the solution for the triangle. Since you are six feet tall, the total height of the bird in the sky is 173.8 feet.

Example $\PageIndex{7}$

While out swimming one day you spot a coin at the bottom of the pool. The pool is ten feet deep, and the angle between the top of the water and the coin is $15^{\circ}$. How far away is the coin from you along the bottom of the pool?

Solution

Since the distance along the bottom of the pool to the coin is the same as the distance along the top of the pool to the coin, we can use the tangent function to solve for the distance to the coin:

$\begin{aligned} tan15^{\circ}&=\dfrac{\text{opposite}}{\text{adjacent}} \\ tan 15^{\circ} =\dfrac{10}{x} \\ x&=\dfrac{10}{tan15^{\circ}} \\ x&\approx 37.32^{\circ}\end{aligned}$

Example $\PageIndex{8}$

You are hiking and come to a cliff at the edge of a ravine. In the distance you can see your campsite at the base of the cliff, on the other side of the ravine. You know that the distance across the ravine is 500 meters, and the angle between your horizontal line of sight and your campsite is $25^{\circ}$. How high is the cliff? (Assume you are five feet tall.)

Solution

Using the information given, we can construct a solution:

$\begin{aligned} tan 25^{\circ} =\dfrac{\text{opposite}}{\text{adjacent}}\\ tan25^{\circ}&=\dfrac{height}{500} \\ height&=\dfrac{500}{tan25^{\circ}}\\ height&=(500)(.466) \\ height&=233\text{ meters}\end{aligned}$

This is the total height from the bottom of the ravine to your horizontal line of sight. Therefore, to get the height of the ravine, you should take away five feet for your height, which gives an answer of 228 meters.

Review

A 70 foot building casts an 50 foot shadow. What is the angle that the sun hits the building?
You are standing 10 feet away from a tree, and you measure the angle of elevation to be $65^{\circ}$. How tall is the tree? Assume you are 5 feet tall up to your eyes.
Kaitlyn is swimming in the ocean and notices a coral reef below her. The angle of depression is $35^{\circ}$ and the depth of the ocean, at that point is 350 feet. How far away is she from the reef?
The angle of depression from the top of a building to the base of a car is $60^{\circ}$. If the building is 78 ft tall, how far away is the car?

Vocabulary

Term	Definition
Angle of Depression	The angle of depression is the angle formed by a horizontal line and the line of sight down to an object when the image of an object is located beneath the horizontal line.
Angle of Elevation	The angle of elevation is the angle formed by a horizontal line and the line of sight up to an object when the image of an object is located above the horizontal line.

Additional Resources

Interactive Element

Video: Example: Determine What Trig Function Relates Specific Sides of a Right Triangle

Practice: Angles of Elevation and Depression