1.5: Measuring Rotation

Last updated
Save as PDF

Page ID: 61223

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Identify and draw angles of rotation.
Identify quadrantal angles.
Identify co-terminal angles.

Introduction to Angles of Rotation, Coterminal Angles, and Reference Angles

Angles of Rotation

Angles of rotation are formed in the coordinate plane between the positive $x$-axis (initial side) and a ray (terminal side). Positive angle measures represent a counterclockwise rotation while negative angles indicate a clockwise rotation.

$Screen Shot 2021-04-16 at 18.39.15.png$ Figure $\PageIndex{1}$

Since the $x$ and $y$ axes are perpendicular, each axis then represents an increment of ninety degrees of rotation. The diagrams below show a variety of angles formed by rotating a ray through the quadrants of the coordinate plane.

$Screen Shot 2021-04-16 at 18.39.37.png$ Figure $\PageIndex{2}$

An angle of rotation can be described infinitely many ways. It can be described by a positive or negative angle of rotation or by making multiple full circle rotations through $360^{\circ}$. The example below illustrates this concept.

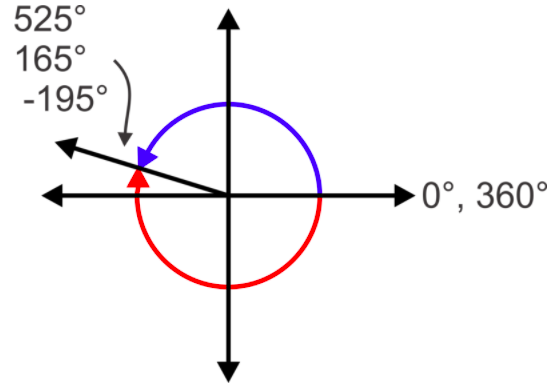$Screen Shot 2021-04-16 at 18.27.46.png$ Figure $\PageIndex{3}$

For the angle $525^{\circ}$, an entire $360^{\circ}$ rotation is made and then we keep going another $165^{\circ}$ to $525^{\circ}$. Therefore, the resulting angle is equivalent to $525^{\circ}−360^{\circ}$, or $165^{\circ}$. In other words, the terminal side is in the same location as the terminal side for a $165^{\circ}$ angle. If we subtract $360^{\circ}$ again, we get a negative angle, $−195^{\circ}$. Since they all share the same terminal side, they are called coterminal angles.

Let's determine two coterminal angles to $837^{\circ}$, one positive and one negative.

To find coterminal angles we simply add or subtract $360^{\circ}$ multiple times to get the angles we desire. $837^{\circ}−360^{\circ}=477^{\circ}$, so we have a positive coterminal angle. Now we can subtract $360^{\circ}$ again to get $477^{\circ}−360^{\circ}=117^{\circ}$.

Reference Angle

A reference angle is the acute angle between the terminal side of an angle and the $x $– axis. The diagram below shows the reference angles for terminal sides of angles in each of the four quadrants.

Note: A reference angle is never determined by the angle between the terminal side and the $y$ – axis. This is a common error for students, especially when the terminal side appears to be closer to the $y$ – axis than the $x$ – axis.

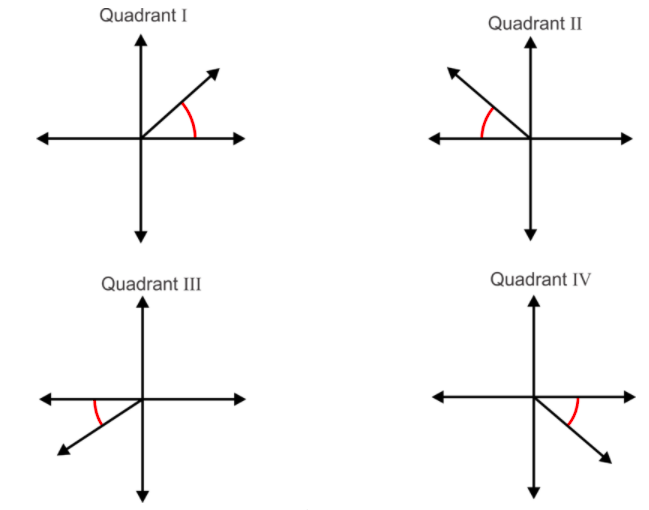$Screen Shot 2021-04-16 at 18.28.07.png$ Figure $\PageIndex{4}$

Now, let's determine the quadrant in which $−745^{\circ}$ lies and hence determine the reference angle.

Since our angle is more than one rotation, we need to add $360^{\circ}$ until we get an angle whose absolute value is less than \)$360^{\circ}$: $−745^{\circ}+360^{\circ}=−385^{\circ}$, again $−385^{\circ}+360^{\circ}=−25^{\circ}$.

Now we can plot the angle and determine the reference angle:

Note that the reference angle is positive $25^{\circ}$. All reference angles will be positive as they are acute angles (between $0^{\circ}$ and$90^{\circ}$).

$Screen Shot 2021-04-16 at 18.28.19.png$ Figure $\PageIndex{5}$

Finally, let's give two coterminal angles to \(595^{\circ}, one positive and one negative, and find the reference angle.

To find the coterminal angles we can add/subtract $360^{\circ}$. In this case, our angle is greater than $360^{\circ}$ so it makes sense to subtract $360^{\circ}$ to get a positive coterminal angle: $595^{\circ}−360^{\circ}=235^{\circ}$. Now subtract again to get a negative angle: $235^{\circ}−360^{\circ}=−125^{\circ}$.

By plotting any of these angles we can see that the terminal side lies in the third quadrant as shown.

Since the terminal side lies in the third quadrant, we need to find the angle between $180^{\circ}$ and $235^{\circ}$, so $235^{\circ}−180^{\circ}=55^{\circ}$.

$Screen Shot 2021-04-16 at 18.28.30.png$ Figure $\PageIndex{6}$

Example $\PageIndex{1}$

Earlier, you were asked to find the reference angle of $−500^{\circ}$ and find the quadrant in which the terminal side lies.

Solution

Since our angle is more than one rotation, we need to add $360^{\circ}$ until we get an angle whose absolute value is less than $360^{\circ}$: $−500^{\circ}+360^{\circ}=−200^{\circ}$.

If we plot this angle we see that it is $−200^{\circ}$ clockwise from the origin or $160^{\circ}$ counterclockwise. $160^{\circ}$ lies in the second quadrant.

Now determine the reference angle: $180^{\circ}−160^{\circ}=20^{\circ}$.

Example $\PageIndex{2}$

Find two coterminal angles to $138^{\circ}$, one positive and one negative.

Solution

$138^{\circ}+360^{\circ}=498^{\circ}$ and $138^{\circ}−360^{\circ}=−222^{\circ}$

Example $\PageIndex{3}$

Find the reference angle for $895^{\circ}$.

Solution

$895^{\circ}−360^{\circ}=535^{\circ}$, $535^{\circ}−360^{\circ}=175^{\circ}$. The terminal side lies in the second quadrant, so we need to determine the angle between $175^{\circ}$ and $180^{\circ}$, which is $5^{\circ}$.

Example $\PageIndex{4}$

Find the reference angle for $343^{\circ}$.

Solution

$343^{\circ}$ is in the fourth quadrant so we need to find the angle between $343^{\circ}$ and $360^{\circ}$ which is $17^{\circ}$.

Review

Find two coterminal angles to each angle measure, one positive and one negative.

$−1022^{\circ}$
$354^{\circ}$
$−7^{\circ}$

Determine the quadrant in which the terminal side lies and find the reference angle for each of the following angles.

4. $251^{\circ}$

5. $−348^{\circ}$

Additional Resources

Interactive Element