22.10: Dividir polinomios
- Page ID
- 127771
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dividiendo Un Polinomio Por Un Monomio
Los siguientes ejemplos ilustran cómo dividir un polinomio por un monomio. El proceso de división es bastante sencillo y se basa en la adición de expresiones racionales.
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\)
Dando la vuelta a esta ecuación obtenemos
\(\dfrac{a+b}{c} = \dfrac{a}{c} + \dfrac{b}{c}\)
Ahora simplemente\(c\) dividimos en\(a\), y\(c\) en\(b\). Esto debería sugerir una regla.
Para dividir un polinomio por un monomio, dividir cada término del polinomio por el monomio.
Conjunto de Muestras A
\(\dfrac{3x^2 + x - 11}{x}\). Dividir cada término de\(3x^2 + x - 11\) por\(x\).
\(\dfrac{3x^2}{x} + \dfrac{x}{x} - \dfrac{11}{x} = 3x + 1 - \dfrac{11}{x}\)
\(\dfrac{8x^3 + 4a^2 - 16a + 9}{2a^2}. Divide every term of \(8a^3 + 4a^2 - 16a + 9\)por\(2a^2\).
\(\dfrac{4b^6 - 9b^4 - 2b + 5}{-4b^2}\). Dividir cada término de\(4b^6 - 9b^4 - 2b + 5\) por\(-4b^2\).
\(\dfrac{4b^6}{-4b^2} - \dfrac{9b^4}{-4b^2} - \dfrac{2b}{-4b^2} + \dfrac{5}{-4b^2} = -b^4 + \dfrac{9}{4}b^2 + \dfrac{1}{2b} - \dfrac{5}{4b^2}\)
Conjunto de práctica A
Realizar las siguientes divisiones.
\(\dfrac{2x^2 + x - 1}{x}\)
- Contestar
-
\(2x + 1 - \dfrac{1}{x}\)
\(\dfrac{3x^3 + 4x^2 + 10x - 4}{x^2}\)
- Contestar
-
\(3x + 4 + \dfrac{10}{x} - \dfrac{4}{x^2}\)
\(\dfrac{a^2b + 3ab^2 + 2b}{ab}\)
- Contestar
-
\(a + 3b + \dfrac{2}{a}\)
\(\dfrac{14x^2y^2 - 7xy}{7xy}\)
- Contestar
-
\(2xy−1\)
\(\dfrac{10m^3n^2 + 15m^2n^3 - 20mn}{-5m}\)
- Contestar
-
\(-2m^2n^2 - 3mn^3 + 4n\)
El Proceso De División
En la Sección 8.3 se estudió el método de reducción de expresiones racionales. Por ejemplo, observamos cómo reducir una expresión como
\(\dfrac{x^2 - 2x - 8}{x^2 - 3x - 4}\)
Nuestro método fue factorizar tanto el numerador como el denominador, luego dividir los factores comunes.
\(\dfrac{(x-4)(x+2)}{(x-4)(x+1)}\)
\(\dfrac{\cancel{(x-4)}(x+2)}{\cancel{(x-4)}(x+1)}\)
\(\dfrac{x+2}{x+1}\)
Cuando el numerador y el denominador no tienen factores en común, la división aún puede ocurrir, pero el proceso está un poco más involucrado que simplemente factorizar. El método de dividir un polinomio por otro es muy similar al de dividir un número por otro. Primero, revisaremos los pasos para dividir números.
\(\dfrac{35}{8}\). Estamos para dividir 35 por 8.
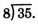Intentamos 4, ya que 32 dividido por 8 es 4.
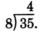Multiplicar 4 y 8
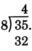Restar 32 de 35
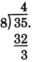Dado que el resto 3 es menor que el divisor 8, terminamos con la división 32.
\(4\dfrac{3}{8}\). El cociente se expresa como un número mixto.
El proceso consistió en dividir, multiplicar y restar.
Revisión De Resta De Polinomios
Un paso muy importante en el proceso de dividir un polinomio por otro es la resta de polinomios. Revisemos el proceso de resta observando algunos ejemplos.
1. Restar\(x -2\) de\(x-5\); es decir, encontrar\((x-5) - (x-2)\).
Ya que\(x-2\) va precedido de un signo menos, elimine los paréntesis, cambie el signo de cada término, luego agregue.
\ (\ begin {array} {ruedado}
x-5 && x-5\\
- (x-2) && -x+2\\
\ text {_______} & = &\ text {_______}\\
&&-3
\ end {array}\\)
El resultado es\(-3\)
2. Restar\(x^3 + 3x^2\) de\(x^3 + 4x^2 + x - 1\).
Ya que\(x^3 + 3x^2\) va precedido de un signo menos, elimine los paréntesis, cambie el signo de cada término, luego agregue.
\ (\ begin {array} {ras a la izquierda}
x^3 + 4x^2 + x - 1 && x^3 + 4x^2 + x - 1\\
- (x^3 + 3x^2) && -x^3 - 3x^2\
\ text {_______________} & = &\ text {_______________}\\
&&x^2 + x - 1
\ end {array}\)
El resultado es\(x^2 + x - 1\)
3. Restar\(x^2 + 3x\) de\(x^2 + 1\)
Podemos escribir\(x^2 + 1\) como\(x^2 + 0x + 1\).
\ (\ begin {array} {ras a la izquierda}
x^2 + 1 && x^2 + 0x + 1 && x^2 + 0x + 1\\
- (x^2 + 3x) && - (x^2 + 3x) && -x^2 - 3x\
\\ text {____________} & = &\ text {____________} & = &\ texto {____________}\
&&&& -3x + 1
\ end {array}\)
Dividiendo Un Polinomio Por Un Polinomio
Ahora vamos a observar algunos ejemplos de dividir un polinomio por otro. El proceso es el mismo que el proceso utilizado con números enteros: dividir, multiplicar, restar, dividir, multiplicar, restar,...
La división, multiplicación y resta tienen lugar un término a la vez. El proceso se concluye cuando el resto polinómico es de menor grado que el divisor polinómico.
Conjunto de Muestras B
Realizar la división.
\(\dfrac{x-5}{x-2}\). Tenemos que dividirnos\(x-5\) por\(x-2\).
\(1 - \dfrac{3}{x-2}\)
Por lo tanto,
\(\dfrac{x-5}{x-2} = 1 - \dfrac{3}{x-2}\)
\(\dfrac{x^3 + 4x^2 + x - 1}{x + 3}\). Tenemos que dividirnos\(x^3 + 4x^2 + x - 1\) por\(x + 3\).
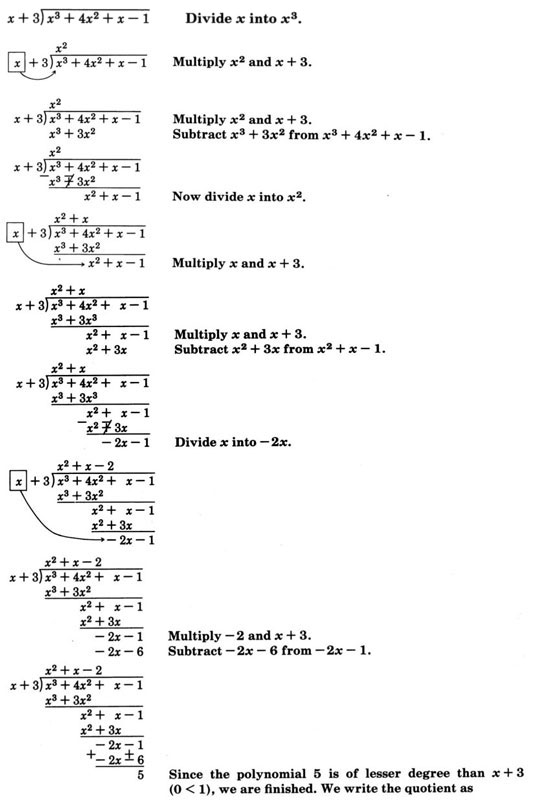
\(x^2 + x - 2 + \dfrac{5}{x+3}\)
Por lo tanto,
\(\dfrac{x^3 + 4x^2 + x - 1}{x + 3} = x^2 + x - 2 + \dfrac{5}{x+3}\)
Set de práctica B
Realizar las siguientes divisiones.
\(\dfrac{x+6}{x-1}\)
- Contestar
-
\(1 + \dfrac{7}{x-1}\)
\(\dfrac{x^2 + 2x + 5}{x + 3}\)
- Contestar
-
\(x - 1 + \dfrac{8}{x+3}\)
\(\dfrac{x^3 + x^2 - x - 2}{x + 8}\)
- Contestar
-
\(x^2 - 7x + 55 - \dfrac{442}{x+8}\)
\(\dfrac{x^3 + x^2 - 3x + 1}{x^2 + 4x - 5}\)
- Contestar
-
\(x - 3 + \dfrac{14x - 14}{x^2 + 4x - 5} = x - 3 + \dfrac{14}{x+5}\)
Conjunto de Muestras C
Dividir\(2x^3 - 4x + 1\) por\(x + 6\)
\(\dfrac{2x^3 - 4x + 1}{x + 6}\)Observe que falta el\(x^2\) término en el numerador. Podemos evitar cualquier confusión escribiendo
\(\dfrac{2x^3 + 0x^2 - 4x + 1}{x+6}\)Dividir, multiplicar y restar.
\(\dfrac{2x^3 - 4x + 1}{x + 6} = 2x^3 - 12x + 68 - \dfrac{407}{x + 6}\)
Set de práctica C
Realizar las siguientes divisiones.
\(\dfrac{x^2 - 3}{x+2}\)
- Contestar
-
\(x - 2 + \dfrac{1}{x+2}\)
\(\dfrac{4x^2 - 1}{x-3}\)
- Contestar
-
\(4x + 12 + \dfrac{35}{x-3}\)
\(\dfrac{x^3 + 2x + 2}{x-2}\)
- Contestar
-
\(x^2 + 2x + 6 + \dfrac{14}{x-2}\)
\(\dfrac{6x^3 + 5x^2 - 1}{2x + 3}\)
- Contestar
-
\(3x^2 - 2x + 3 - \dfrac{10}{2x + 3}\)
Ejercicios
Para los siguientes problemas, realizar las divisiones.
\(\dfrac{6a + 12}{2}\)
- Contestar
-
\(3a+6\)
\(\dfrac{12b - 6}{3}\)
\(\dfrac{8y - 4}{-4}\)
- Contestar
-
\(−2y+1\)
\(\dfrac{21a - 9}{-3}\)
\(\dfrac{3x^2 - 6x}{-3}\)
- Contestar
-
\(−x(x−2)\)
\(\dfrac{4y^2 - 2y}{2y}\)
\(\dfrac{9a^2 + 3a}{2a}\)
- Contestar
-
\(3a+1\)
\(\dfrac{20x^2 + 10x}{5x}\)
\(\dfrac{6x^3 + 2x^2 + 8x}{2x}\)
- Contestar
-
\(3x^2 + x + 4\)
\(\dfrac{26y^3 + 13y^2 + 39y}{13y}\)
\(\dfrac{a^2b^2 + 4a^2b + 6ab^2 - 10ab}{ab}\)
- Contestar
-
\(ab+4a+6b−10\)
\(\dfrac{7x^3y + 8x^2y^3 + 3xy^4 - 4xy}{xy}\)
\(\dfrac{5x^3y^3 - 15x^2y^2 + 20xy}{-5xy}\)
- Contestar
-
\(-x^2y^2 + 3xy - 4\)
\(\dfrac{4a^2b^3 - 8ab^4 + 12ab^2}{-2ab^2}\)
\(\dfrac{6a^2y^2 + 12a^2y + 18a^2}{24a^2}\)
- Contestar
-
\(\dfrac{1}{4}y^2 + \dfrac{1}{2}y + \dfrac{3}{4}\)
\(\dfrac{3c^3y^3 + 99c^3y^4 - 12c^3y^5}{3x^3y^3}\)
\(\dfrac{16ax^2 - 20ax^3 + 24ax^4}{6a^4}\)
- Contestar
-
\(\dfrac{8x^2 - 10x^3 + 12x^4}{3a^3}\)o\(\dfrac{12x^4 - 10x^3 + 8x^2}{3a^2}\)
\(\dfrac{21ay^3 - 18ay^2 - 15ay}{6ay^2}\)
\(\dfrac{-14b^2c^2 + 21b^3 - 28c^3}{-7a^2c^3}\)
- Contestar
-
\(\dfrac{2b^2 - 3b^3c + 4c}{a^2c}\)
\(\dfrac{-30a^2b^4 - 35a^2b^3 - 25a^2}{-5b^3}\)
\(\dfrac{x+6}{x-2}\)
- Contestar
-
\(1 + \dfrac{8}{x-2}\)
\(\dfrac{y + 7}{y + 1}\)
\(\dfrac{x^2 - x + 4}{x + 2}\)
- Contestar
-
\(x - 3 + \dfrac{10}{x+2}\)
\(\dfrac{x^2 + 2x - 1}{x + 1}\)
\(\dfrac{x^2 - x + 3}{x + 1}\)
- Contestar
-
\(x - 2 + \dfrac{5}{x + 1}\)
\(\dfrac{x^2 + 5x + 5}{x + 5}\)
\(\dfrac{x^2 - 2}{x + 1}\)
- Contestar
-
\(x - 1 - \dfrac{1}{x+1}\)
\(\dfrac{a^2 - 6}{a + 2}\)
\(\dfrac{y^2 + 4}{y + 2}\)
- Contestar
-
\(y - 2 + \dfrac{8}{y + 2}\)
\(\dfrac{x^2 + 36}{x + 6}\)
\(\dfrac{x^3 - 1}{x + 1}\)
- Contestar
-
\(x^2 - x + 1 - \dfrac{2}{x + 1}\)
\(\dfrac{a^3 - 8}{a + 2}\)
\(\dfrac{x^3 + 3x^2 + x - 2}{x-2}\)
- Contestar
-
\(x^2 + 5x + 11 + \dfrac{20}{x-2}\)
\(\dfrac{a^3 + 2a^2 - a + 1}{a - 3}\)
\(\dfrac{x^3 + 2x + 1}{x - 3}\)
\(\dfrac{y^3 + 2y^2 + 4}{y + 2}\)
- Contestar
-
\(y^2 + y - 2 + \dfrac{8}{y + 2}\)
\(\dfrac{y^3 + 5y^2 - 3}{y - 1}\)
\(\dfrac{x^3 + 3x^2}{x + 3}\)
- Contestar
-
\(x^2\)
\(\dfrac{a^2 + 2a}{a + 2}\)
\(\dfrac{x^2 - x - 6}{x^2 - 2x - 3}\)
- Contestar
-
\(1 + \dfrac{1}{x + 1}\)
\(\dfrac{a^2 + 5a + 4}{a^2 - a - 2}\)
\(\dfrac{2y^2 + 5y + 3}{y^2 - 3y - 4}\)
- Contestar
-
\(2 + \dfrac{11}{y-4}\)
\(\dfrac{3a^2 + 4a + 2}{3a + 4}\)
\(\dfrac{6x^2 + 8x - 1}{3x + 4}\)
- Contestar
-
\(2x - \dfrac{1}{3x + 4}\)
\(\dfrac{20y^2 + 15y - 4}{4y + 3}\)
\(\dfrac{4x^3 + 4x^2 - 3x - 2}{2x - 1}\)
- Contestar
-
\(2x^2 + 3x - \dfrac{2}{2x - 1}\)
\(\dfrac{9a^3 - 18a^2 8a - 1}{3a - 2}\)
\(\dfrac{4x^4 - 4x^3 + 2x^2 - 2x - 1}{x-1}\)
- Contestar
-
\(4x^3 + 2x - \dfrac{1}{x-1}\)
\(\dfrac{3y^4 + 9y^3 - 2y^2 - 6y + 4}{y + 3}\)
\(\dfrac{3y^2 + 3y + 5}{y^2 + y + 1}\)
- Contestar
-
\(3 + \dfrac{2}{y^2 + y + 1}\)
\(\dfrac{2a^2 + 4a + 1}{a^2 + 2a + 3}\)
\(\dfrac{8z^6 - 4z^5 - 8z^4 + 8z^3 + 3z^2 - 14z}{2z - 3}\)
- Contestar
-
\(4z^5 + 4z^4 + 2z^3 + 7z^2 + 12z + 11 + \dfrac{33}{2z - 3}\)
\(\dfrac{9 a^{7}+15 a^{6}+4 a^{5}-3 a^{4}-a^{3}+12 a^{2}+a-5}{3 a+1}\)
\((2x^5 + 5x^4 -1) \div (2x + 5)\)
- Contestar
-
\(x^4 - \dfrac{1}{2x + 5}\)
\((6a^4 - 2a^3 - 3a^2 + a + 4) \div (3a - 1)\)
Ejercicios para revisión
Encuentra el producto. \(\dfrac{x^2 + 2x - 8}{x^2 - 9} \cdot \dfrac{2x + 6}{4x - 8}\)
- Contestar
-
\(\dfrac{x + 4}{2(x-3)}\)
Encuentra la suma. \(\dfrac{x-7}{x + 5} + \dfrac{x + 4}{x - 2}\)
Resolver la ecuación\(\dfrac{1}{x + 3} + \dfrac{1}{x - 3} = \dfrac{1}{x^2 - 9}\)
- Contestar
-
\(x = \dfrac{1}{2}\)
Cuando se resta el mismo número tanto del numerador como del denominador de\(dfrac{3}{10}\), el resultado es\(\dfrac{1}{8}\). ¿Cuál es el número que se resta?
Simplificar\(\dfrac{\frac{1}{x+5}}{\frac{4}{x^{2}-25}}\)
- Contestar
-
\(\dfrac{x-5}{4}\)