24.7: Aplicaciones
- Page ID
- 127793
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El método de cinco pasos
Ahora estamos en condiciones de estudiar algunas aplicaciones de las ecuaciones cuadráticas. Las ecuaciones cuadráticas pueden surgir de una variedad de problemas físicos (aplicados) y matemáticos (lógicos).
Volveremos a aplicar el método de cinco pasos para resolver problemas verbales.
- Paso 1: Que\(x\) (o alguna otra letra) represente la cantidad desconocida.
- Paso 2: Traducir la expresión verbal a símbolos matemáticos y formar una ecuación.
- Paso 3: Resuelve esta ecuación.
- Paso 4: Verifique la solución sustituyendo el resultado en la ecuación que se encuentra en el paso 2.
- Paso 5: Escribe una conclusión.
Recuerda, el paso 1 es muy importante.
Comience siempre introduciendo una variable
Una vez desarrollada la ecuación cuadrática (paso 2), intenta resolverla factorizando. Si la factorización no funciona, usa la fórmula cuadrática. Una calculadora puede ayudar a que algunos de los cálculos sean un poco menos tediosos.
Conjunto de Muestras A
Un productor de cubiertas de ratón de computadora personal determina que el número\(N\) de cubiertas vendidas está relacionado con el precio\(x\) de una cubierta por\(N = 35x - x^2\). ¿A qué precio debería el productor poner un precio a un ratón para poder vender\(216\) de ellos?
\ (\ begin {array} {vaciado a la izquierda}
\ text {Paso 1:} &\ text {Dejar} x=\ texto {el precio de una cubierta de ratón.} \\
\ text {Paso 2:} &\ text {Desde} N\ text {va a ser} 216\ text {, la ecuación es}\\
& 216 = 35x - x^2
\ end {array}\)
\ (\ begin {array} {flushleft}
\ text {Paso 3:} & 216 &= 35x - x^2 &\ text {Reescribir en forma estándar}\\
& x^2 - 35x + 216 &= 0 &\ text {Intenta factorizar.}\\
& (x-8) (x-27) &= 0\\
& x-8 = 0 &\ text {o} x-27=0\\
& x = 8 &\ text {o} x=27
\ end {array}\)
Compruebe estos potenciales soluciones.
\ (\ begin {array} {lavadoizquierdo}
\ text {Paso 4:} &\ text {Si} x=8, & & &\ text {Si} x = 27\\
& 35\ cdot 8 &= 216 &\ text {¿Es esto correcto? } & 35\ cdot 27 - 27^2 &= 216 &\ text {¿Es correcto? }\\
& 280 - 64 &= 216 &\ text {¿Es esto correcto? } & 945 - 729 &= 216 &\ text {¿Es correcto? }\\
& 216 &= 216 &\ text {Sí, esto es correcto.} & 216 &= 216 &\ text {Sí, esto es correcto.}\\
\ end {array}\)
Estas soluciones verifican.
Paso 5: Las cubiertas del mouse de computadora pueden tener un precio de $8 o $27 para poder vender 216 de ellas.
Conjunto de práctica A
Un fabricante de fundas antipolvo de tela para computadora personal advierte que el número\(N\) de cubiertas vendidas está relacionado con el precio de las cubiertas por\(N = 30x - x^2\). ¿A qué precio debe el fabricante poner el precio de las cubiertas para poder\(216\) venderlas?
Paso 1:
Paso 2:
Paso 3:
Paso 4:
Paso 5: Para vender 216 cubiertas, el fabricante debe ponerles un precio a cualquiera o.
- Responder
-
12 o 18
Se estima que dentro de\(t\) años la población de una ciudad en particular será
\(P = t^2 - 24t + 96000\)
¿Cuántos años a partir de ahora la población será de 95,856?
Paso 1:
Paso 2:
Paso 3:
Paso 4:
Paso 5:
- Responder
-
En 9 y 15 años, la población de la ciudad será de 95 mil 865.
Conjunto de Muestras B
La longitud de un rectángulo es de 4 pulgadas más del doble de su ancho. El área es de 30 pulgadas cuadradas. Encuentra las dimensiones (largo y ancho).
Paso 1: Deja que\(x=\) el ancho. Entonces,\(2x + 4 = \) la longitud.
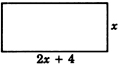
Paso 2: El área de a se define como la longitud del rectángulo multiplicada por el ancho del rectángulo. Por lo tanto,
\(x(2x + 4) = 30\)
\ (\ begin {array} {lavado a la izquierda}
\ texto {Paso 3:} & x (2x + 4) &= 30\\
& 2x^2 + 4x &= 30\\
& 2x^2 + 4x - 30 &= 0 &\ text {Divide cada lado por} 2\\
& x^2 + 2x - 15 &= 0 &\ text {Factor.}\\
& (x+5) (x-3) &= 0
& x &= -5, 3\\
& x & -5 &\ text {no tiene significado físico así que lo ignoramos. Comprobar} x=3\\
& x &= 3
\ end {array}\)
\(2x + 4 = 2 \cdot 3 + 4 = 10\)
\ (\ begin {array} {vaciado a la izquierda}
\ text {Paso 4:} & x (2x + 4) &= 30 &\ text {¿Es esto correcto?} \\
& 3 (2\ cdot 3 + 4) &= 30 &\ text {¿Es esto correcto?} \\
& 3 (6 + 4) &= 30 &\ text {¿Es esto correcto?} \\
& 3 (10) &= 30 &\ text {¿Es esto correcto?} \\
& 30 &= 30 &\ text {Sí, esto es correcto}
\ end {array}\)
Paso 5: Ancho\(= 3\) pulgadas y Largo\(= 10\) Pulgadas.
Set de práctica B
La longitud de un rectángulo es de 3 pies más del doble de su ancho. El área es de 14 pies cuadrados. Encuentra las dimensiones.
- Responder
-
ancho = 2 pies, largo = 7 pies
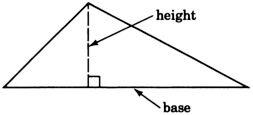
El área de un triángulo es de 24 metros cuadrados. La base es 2 metros más larga que la altura. Encuentra la base y la altura. La fórmula para el área de un triángulo es\(A = \dfrac{1}{2} b \cdot h\).
- Responder
-
altura = 6 metros, base = 8 metros
Conjunto de Muestras C
El producto de dos enteros consecutivos es 156. Encuéntralos
\ (\ begin {array} {vaciado a la izquierda}
\ text {Paso 1:} &\ text {Let} x &=\ text {el entero más pequeño.} \\
& x + 1 &=\ texto {el siguiente entero}\\
\ texto {Paso 2:} x (x + 1) &= 156\\
\ texto {Paso 3:} x (x + 1) &= 156\\
& x^2 + x &= 156\\
& x^2 + x - 156 &= 0\\
& (x-12) (x - 13) &= 0\\
& x &= 12, -13
\ end {array}\)
Esta factorización puede ser difícil de adivinar. También podríamos haber utilizado la fórmula cuadrática.
\ (\ begin {array} {lavadoizquierdo}
\ text {Paso 4:} &\ text {Si} x=12: & 12 (2 + 1) &= 156 &\ text {¿Es esto correcto?} \\
& & 12 (13) &= 156 &\ text {¿Es esto correcto?} \\
& & 156 &= 156 &\ text {Sí, esto es correcto}\\
&\ text {Si} x=-13 & -13 (-13 + 1) &= 156 &\ text {¿Es esto correcto?} \\
& & -13 (-12) &= 156 &\ text {¿Es esto correcto?} \\
& & 156 &= 156 &\ text {Sí, esto es correcto.}
\ end {array}\)
Paso 5: Hay dos soluciones:\(12, 13\), y\(-13, -12\)
Set de práctica C
El producto de dos enteros consecutivos es 210. Encuéntralos.
- Responder
-
14 y 15, y —14 y —15
Cuatro se agrega a un entero y esa suma se triplica. Cuando este resultado se multiplica por el entero original, el producto es −12. Encuentra el entero.
- Contestar
-
—2
Conjunto de Muestras D
Una caja sin tapa y base cuadrada se va a hacer cortando cuadrados de 2 pulgadas de cada esquina y plegando los lados de un trozo de cartón cuadrado. El volumen de la caja debe ser de 8 pulgadas cúbicas. ¿De qué tamaño debe ser el trozo de cartón?
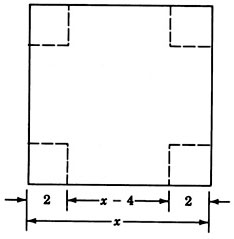
Paso 1: Dejar que\(x=\) el largo (y ancho) de la pieza de cartón.
Paso 2: El volumen de una caja rectangular es
\(V = \text{(length) (width) (height)}\)
\(8 = (x-4)(x-4)2\)
\ (\ begin {array} {arrojado a la izquierda}
\ texto {Paso 3:} & 8 =( x-4) (x-4) 2\\
& 8 =( x^2 - 8x + 16) 2\\
& 8=2x^2 - 16x + 32\\
& 2x^2 - 16x + 24 = 0 &\ text {Divide cada lado por} 2\\
& x^2 - 8x + 12 = 0 &\ text {Factor.} \\
& (x-6) (x-2) = 0
& x = 6, 2
\ end {array}\)
\(x\)no puede igualar\(2\) (el corte pasaría por el trozo de cartón). Cheque\(x = 6\).
\ (\ begin {array} {surcos a la izquierda}
\ text {Paso 4:} & (6 - 4) (6 - 4) 2 &= 8 &\ text {¿Es esto correcto?} \\
& (2) (2) 2 &= 8 &\ text {¿Es esto correcto?} \\
& 8&=8 &\ text {Sí, esto es correcto.}
\ end {array}\)
Paso 5: El trozo de cartón debe ser de 6 pulgadas por 6 pulgadas.
Set de Práctica D
Una caja sin tapa y base cuadrada se va a hacer cortando cuadrados de 3 pulgadas de cada esquina y plegando los lados de un trozo de cartón. El volumen de la caja debe ser de 48 pulgadas cúbicas. ¿De qué tamaño debe ser el trozo de cartón?
- Contestar
-
10 pulg. por 10 pulg.; 2 por 2 no es físicamente posible.
Juego de Muestras E
Un estudio de la calidad del aire en una ciudad en particular realizado por un grupo ambiental sugiere que dentro de\(t\) años el nivel de monóxido de carbono, en partes por millón, en el aire será
\(A = 0.3t^2 + 0.1t + 4.2\)
a) ¿Cuál es el nivel, en partes por millón, de monóxido de carbono en el aire ahora?
Ya que la ecuación\(A = 0.3t^2 + 0.1t + 4.2\) especifica el nivel\(t\) años a partir de ahora, tenemos\(t = 0\).
\ (A = 0.3t^2 + 0.1t + 4.2\\
A = 4.2\)
b) ¿Cuántos años a partir de ahora estará el nivel de monóxido de carbono en 8 partes por millón?
\ (\ begin {array} {ras a la izquierda}
\ text {Paso 1:} & t &=\ text {el número de yeras cuando el nivel es} 8\\
\ text {Paso 2:} & 8 &= 0.3t^2 + 0.1t + 4.2\\
\ text {Paso 3:} & 8 &= 0.3t^2 + 0.1t + 4.2\\ & 0 &= 0.3t^2 + 0.1t + 4.2\\
& 0 &= 0.3t^^2 + 0.1t - 3.8 & \ text {Esto no factoriza fácilmente, así que usaremos la fórmula cuadrática.}\\
& a &= 0.3, b = 0.1, c = -3.8\\
& t &=\ dfrac {-0.1\ pm\ sqrt {(0.1) ^2 = 4 (0.3) (-3.8)}} {2 (0.3)}\\
& &=\ dfrac {-0.1\ pm\ sqrt {0.01 + 4.56}} {0.6} =\ dfrac {-0.1\ pm\ sqrt {4. 57}} {0.6}\\
& &=\ dfrac {-0.1\ pm 2.14} {0.6}\\
& t &= 3.4\ text {and} -3.73
\ end {array}\) no
\(t = -3.73\) tiene ningún significado físico. Comprobar\(t = 3.4\)
Paso 4: Este valor de\(t\) ha sido redondeado a la décima más cercana. Si comprueba (bastante de cerca).
Paso 5: Dentro de unos 3.4 años el nivel de monóxido de carbono será\(8\).
Set de práctica E
Un estudio de la calidad del aire en una ciudad en particular por parte de un grupo ambiental sugiere que dentro de t años el nivel de monóxido de carbono, en partes por millón, en el aire será
\(A = 0.2t^2 + 0.1t + 5.1\)
a) ¿Cuál es el nivel, en partes por millón, ahora?
b) ¿Cuántos años a partir de ahora estará el nivel de monóxido de carbono en 8 partes por millón? Redondear a la décima más cercana.
- Contestar
-
a). 5.1 partes por millón
b). 3.6 años
Conjunto de Muestras F
Un contratista debe verter una pasarela de concreto alrededor de una piscina de 20 pies de ancho y 40 pies de largo. El área de la pasarela es de 544 pies cuadrados. Si la pasarela va a ser de ancho uniforme, ¿qué tan ancho debe hacerla el contratista?
Paso 1: Deja que\(x=\) el ancho de la pasarela.
Paso 2: Un diagrama nos ayudará a obtener la ecuación
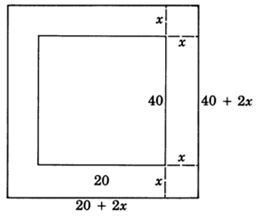
(Área de alberca y pasarela) - (Área de alberca) = (área de pasarela)
\((20 + 2x)(40 + 2x) - 20 \cdot 40 = 544\)
\ (\ begin {array} {arrojado a la izquierda}
\ texto {Paso 3:} & (20 + 2x) (40 + 2x) - 20\ cdot 40 &= 544\\
& 800 + 120x + 4x^2 - 800 &= 544\\
& 120x + 4x^23 &= 544\\
& 4x^2 + 120x - 544 &= 0 &\ text {Divide cada término por} 4\\
& x^2 + 30x - 136 &= 0 &\ text {Resolver factorizando. (o fórmula cuadrática)}\\
& (x-4) (x + 34) &= 0
\ end {array}\)
\ (\ begin {array} {lavado a la izquierda}
x - 4 &= 0 &\ text {o} & x + 34 &= 0\\
x &=4 &\ text {o} & x &= -34\ text {no tiene significado físico}
\ end {array}\)
Verifique un ancho de 4 pies como solución.
\ (\ begin {array} {flushleft}
\ text {Paso 4:} &\ text {Área de alberca y pasarela} &= (20 + 2\ cdot 4) (40 + 2\ cdot 4)\\
& &= (28) (48)\\
& &= 1344
\ end {array}\)
Área de alberca\(=(20)(40) = 800\)
Zona de pasarela\(=1344 - 800 = 544\). Sí, esto es correcto.
Esta solución comprueba.
Paso 5: El contratista debe hacer la pasarela de 4 pies de ancho.
Set de práctica F
Un contratista debe verter una pasarela de concreto alrededor de una piscina de 15 pies de ancho y 25 pies de largo. El área de la pasarela será de 276 pies cuadrados. Si la pasarela va a ser de ancho uniforme, ¿qué tan ancho debe hacerla el contratista?
- Contestar
-
3 pies de ancho
Ejercicios
Algunos de los siguientes problemas tienen aplicaciones reales y algunos están pensados solo como desarrolladores de lógica. Una calculadora puede ser útil. Los problemas aparecen en grupos y corresponden al problema señalado del Conjunto de Muestras.
Problemas de tipo A con el conjunto de muestras
El fabricante de inyectores electrónicos de combustible determina que el número\(N\) de inyectores vendidos está relacionado con el precio\(x\) por inyector por\(N = 22x - x^2\). ¿A qué precio debe el fabricante fijar el precio de los inyectores para que se vendan 112 de ellos?
- Contestar
-
$8 o $14
El dueño de una vitral determina que el número\(N\) de piezas de un determinado tipo de vidrio que se venden en un mes está relacionado con el precio\(x\) por pieza por\(N = 21x - x^2\). ¿A qué precio debe el comprador de la tienda poner el precio al vidrio para que 162 venda?
Se estima que\(t\) dentro de años la población de una determinada ciudad será
\(P = t^2 - 15t + 12036\)
a) ¿Cuál es la población ahora?
b) ¿Cuántos años a partir de ahora será la población de 12 mil?
- Contestar
-
a) 12.036
b) Dentro de 3 y 12 años
Se estima que\(t\) dentro de años la población de una determinada ciudad será
\(P = t^2 - 16t + 24060\)
a) ¿Cuál es la población ahora?
b) ¿Cuántos años a partir de ahora será la población de 24 mil?
Si un objeto es arrojado verticalmente hacia arriba, su altura\(h\), por encima del suelo, en pies, después de\(t\) segundos viene dada por\(h = h_0 + v_0t - 16t^2\), donde\(h_0\) está la altura inicial desde la que se lanza el objeto y\(v_0\) es la velocidad inicial del objeto. Usando esta fórmula y un enfoque como el del Conjunto de Muestras A, resuelve este problema.
Una pelota lanzada verticalmente al aire tiene la ecuación de movimiento\(h = 48 + 32t - 16t^2\).
a) ¿A qué altura está la pelota\(t = 0\) (la altura inicial de la pelota)?
b) ¿A qué altura está la pelota\(t = 1\) (después de 1 segundo en el aire)?
c) ¿Cuándo choca la pelota contra el suelo? (Hind: Determinar el valor apropiado para\(h\) luego resolver para\(t\)).
- Contestar
-
(a) 48 pies
b) 64 pies
c)\(t = 3\)
Las gafas de una mujer se caen accidentalmente de la cara mientras mira por una ventana en un edificio alto. La ecuación que relaciona\(h\), la altura sobre el suelo en pies, y\(t\), el tiempo en segundos que sus gafas han estado cayendo, es\(h = 64 - 16t^2\).
a) ¿Qué tan alto estaba el rostro de la mujer cuando se le cayeron las gafas?
b) ¿Cuántos segundos después de que cayeron las gafas chocaron contra el suelo?
Problemas de tipo B del conjunto de muestras
La longitud de un rectángulo es de 6 pies más del doble de su ancho. El área es de 8 pies cuadrados. Encuentra las dimensiones.
- Contestar
-
longitud=8; ancho=1
La longitud de un rectángulo es de 18 pulgadas más de tres veces su ancho. El área es de 81 pulgadas cuadradas. Encuentra las dimensiones.
La longitud de un rectángulo es de dos tercios de su ancho. El área es de 14 metros cuadrados. Encuentra las dimensiones.
- Contestar
-
ancho =\(\sqrt{21}\); largo =\(\dfrac{2}{3} \sqrt{21}\)
La longitud de un rectángulo es de cuatro novenos su ancho. El área es de 144 pies cuadrados. Encuentra las dimensiones.
El área de un triángulo es de 14 pulgadas cuadradas. La base es 3 pulgadas más larga que la altura. Encuentra tanto la longitud de la base como la altura.
- Contestar
-
\(b=7; h=4\)
El área de un triángulo es de 34 centímetros cuadrados. La base mide 1 cm más larga que el doble de la altura. Encuentra tanto la longitud de la base como la altura
Problemas de tipo C de conjuntos de muestras
El producto de dos enteros consecutivos es 72. Encuéntralos.
- Contestar
-
−9, −8 o 8,9
El producto de dos enteros negativos consecutivos es 42. Encuéntralos.
El producto de dos enteros impares consecutivos es 143. Encuéntralos. (Pista: La ecuación cuadrática es factorizable, pero la fórmula cuadrática puede ser más rápida.)
- Contestar
-
−13, −11 o 11,13
El producto de dos enteros pares consecutivos es 168. Encuéntralos.
Tres se agrega a un entero y esa suma se duplica. Cuando este resultado se multiplica por el entero original el producto es 20. Encuentra el entero.
- Contestar
-
\(n=2,−5\)
Cuatro se agrega a tres veces un número entero. Cuando se multiplican esta suma y el número entero original, el producto es −1. Encuentra el entero.
Problemas del tipo D del conjunto de muestras
Una caja sin tapa y base cuadrada se va a hacer cortando cuadrados de 2 pulgadas de cada esquina y plegando los lados de un trozo de cartón. El volumen de la caja debe ser de 25 pulgadas cúbicas. ¿De qué tamaño debe ser el trozo de cartón?
- Contestar
-
\(4 + \sqrt{12.5}\)pulgadas
Una caja sin tapa y base cuadrada se realiza recortando cuadrados de 8 pulgadas de cada esquina y plegando los lados de un trozo de cartón. El volumen de la caja debe ser de 124 pulgadas cúbicas. ¿De qué tamaño debe ser el trozo de cartón?
Problemas del tipo E del conjunto de muestras
Un estudio de la calidad del aire en una ciudad en particular por parte de un grupo ambiental sugiere que dentro de\(t\) años el nivel de monóxido de carbono, en partes por millón, será\(A = 0.1t^2 + 0.1t + 2.2\).
a) ¿Cuál es el nivel, en partes por millón, de monóxido de carbono en el aire ahora?
b) ¿Cuántos años a partir de ahora estará el nivel de monóxido de carbono en 3 partes por millón?
- Contestar
-
a) Monóxido de carbono actualmente 2.2 partes por millón
b) 2.37 años
Un estudio similar al del problema 21 sugiere\(A = 0.3t^2 + 0.25t + 3.0\)
a) ¿Cuál es el nivel, en partes por millón, de monóxido de carbono en el aire ahora?
b) ¿Cuántos años a partir de ahora estará el nivel de monóxido de carbono en 3 partes por millón?
Problemas del tipo F del conjunto de muestras
Un contratista debe verter una pasarela de concreto alrededor de una piscina para niños que es de 4 pies de ancho y 8 pies de largo. El área de la pasarela y la alberca es para ser de 96 pies cuadrados. Si la pasarela va a ser de ancho uniforme, ¿qué tan amplia debe ser?
- Contestar
-
\(x=2\)
Problema astrofísico
Una aplicación muy interesante de las ecuaciones cuadráticas es determinar la longitud de un eclipse solar (la luna que pasa entre la tierra y el sol). La longitud de un eclipse solar se encuentra resolviendo la ecuación cuadrática
\((a + bt)^2 + (c + dt)^2 = (e + ft)^2\)
para\(t\). Las letras\(a, b, c, d, e\), y\(f\) son constantes que pertenecen a un eclipse particular. La ecuación es una ecuación cuadrática en\(t\) y se puede resolver por la fórmula cuadrática (y definitivamente una calculadora). Resultarán dos valores de\(t\) voluntad. La longitud del eclipse es solo la diferencia\(t\) de estos valores.
Las siguientes constantes son de un eclipse solar ocurrido el 3 de agosto del 431 a.C.
\ (\ begin {array} {ruedado}
a &= -619 & b &= 1438\\
c &= 912 & d &= -833\\
e &= 1890.5 & f&=-2
\ end {array}\)
Determinar la duración de este eclipse solar en particular.
Ejercicios para revisión
Encuentra la suma:\(\dfrac{2x + 10}{x^2 + x - 2} + \dfrac{x + 3}{x^2 - 3x + 2}\)
- Contestar
-
\(\dfrac{3x + 14}{(x+2)(x-2)}\)
Resolver la ecuación fraccionaria\(\dfrac{4}{x+12} + \dfrac{3}{x + 3} = \dfrac{4}{x^2 + 5x + 6}\)
(Pista: Compruebe si hay soluciones extrañas)
Una tubería puede llenar un tanque en 120 segundos y otra tubería puede llenar el mismo tanque en 90 segundos. ¿Cuánto tiempo tardarán ambas tuberías trabajando juntas para llenar el tanque?
- Contestar
-
\(51 \dfrac{3}{7}\)
Usa la fórmula cuadrática para resolver\(10x^2 - 3x - 1 = 0\)
Usa la fórmula cuadrática para resolver\(4x^2 - 3x = 0\)
- Contestar
-
\(x = 0, \dfrac{3}{4}\)


