24.11: Examen de Aptitud

Last updated
Save as PDF

Page ID: 127797

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$\newcommand{\longvect}{\overrightarrow}$

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\ket}[1]{\left| #1 \right>}$
$\newcommand{\bra}[1]{\left< #1 \right|}$
$\newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>}$
$\newcommand{\braopket}[3]{\left< #1 \vphantom{#2}\vphantom{#3} \right| #2 \vphantom{#1}\vphantom{#3} \left| #3 \vphantom{#1}\vphantom{#2} \right>}$
$\newcommand{\qmvec}[1]{\mathbf{\vec{#1}}}$
$\newcommand{\op}[1]{\hat{\mathbf{#1}}}$
$\newcommand{\expect}[1]{\langle #1 \rangle}$
$\newcommand{\dfn}[1]{\emph{\textbf{#1}}}$

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Examen de competencia

Para las ecuaciones cuadráticas en los siguientes problemas, especifique los valores de$a, b$, y$c$.

Ejercicio$\PageIndex{1}$

$2y^2 - 3y + 10 = 0$

Contestar: $a=2,b=−3,c=10$

Ejercicio$\PageIndex{2}$

$10b^2 = 3b$

Contestar: $a=10,b=−3,c=0$

Para los siguientes problemas, utilice la propiedad de factor cero para resolver cada ecuación cuadrática.

Ejercicio$\PageIndex{3}$

$(3x+5)(x−1)=0$

Contestar: $x = -\dfrac{5}{3}, 1$

Ejercicio$\PageIndex{4}$

$3b(2b−1)=0$

Contestar: $b = 0, \dfrac{1}{2}$

Ejercicio$\PageIndex{5}$

$(a - 8)^2 = 0$

Contestar: $a=8$

Para los siguientes problemas, resolver cada ecuación cuadrática por factorización.

Ejercicio$\PageIndex{6}$

$4x^2 - 16 = 0$

Contestar: $x=−2,2$

Ejercicio$\PageIndex{7}$

$y^2 - 12y + 32 = 0$

Contestar: $y=4,8$

Ejercicio$\PageIndex{8}$

$a^2 - 5a = 14$

Contestar: $−2,7$

Ejercicio$\PageIndex{9}$

$6a^2 = 10 - 11a$

Contestar: $a = -\dfrac{5}{2}, \dfrac{2}{3}$

Ejercicio$\PageIndex{10}$

$2x^2 = -2 - 5x$

Contestar: $x = -2, -\dfrac{1}{2}$

Ejercicio$\PageIndex{11}$

$x^3 - 25x = 0$

Contestar: $x=0,−5,5$

Para los siguientes problemas, resolver cada ecuación cuadrática mediante extracción de raíces.

Ejercicio$\PageIndex{12}$

$c^2 = 81$

Contestar: $c=−9,9$

Ejercicio$\PageIndex{13}$

$x^2 = 15$

Contestar: $x = -\sqrt{15}, \sqrt{15}$

Ejercicio$\PageIndex{14}$

$3a^2 - 18 = 0$

Contestar: $a = -\sqrt{6}, \sqrt{6}$

Ejercicio$\PageIndex{15}$

$(x - 5)^2 = 1$

Contestar: $x=4,6$

Ejercicio$\PageIndex{16}$

$(y + 11)^2 - 9 = 0$

Contestar: $y=−8,−14$

Ejercicio$\PageIndex{17}$

$y^2 - 25z^2 = 0$para$y$.

Contestar: $y=−5z,5z$

Ejercicio$\PageIndex{18}$

$6a^2 - 18b^2c^2$para$a$

Contestar: $a = \pm bc\sqrt{3}$

Para los siguientes problemas, resuelve cada ecuación cuadrática usando la fórmula cuadrática.

Ejercicio$\PageIndex{19}$

$x^2 - 6x - 16 = 0$

Contestar: $x=−2,8$

Ejercicio$\PageIndex{20}$

$y^2 - 2y - 7 = 0$

Contestar: $y = 1 + 2\sqrt{2}$

Ejercicio$\PageIndex{21}$

$(m + 2)^2 - 5 = 0$

Contestar: $m = -2 \pm \sqrt{5}$

Ejercicio$\PageIndex{22}$

$(x + b)^2 = c^2$

Contestar: $x = -b \pm c$

Ejercicio$\PageIndex{23}$

$(x+1)(x+4)=6$

Contestar: $x = \dfrac{-5 \pm \sqrt{33}}{2}$

Ejercicio$\PageIndex{24}$

$5z^2 - 5z - 5 = 2z^2 - z$

Contestar: $z = \dfrac{2 \pm \sqrt{19}}{3}$

Ejercicio$\PageIndex{25}$

$2m^2 = 5m$

Contestar: $m = 0, \dfrac{5}{2}$

Para los siguientes problemas, resuelve cada ecuación cuadrática completando el cuadrado.

Ejercicio$\PageIndex{26}$

$x^2 + 6x - 8 = 0$

Contestar: $x = -3 \pm \sqrt{17}$

Ejercicio$\PageIndex{27}$

$2x^2 + 7x - 12 = 0$

Contestar: $x = \dfrac{-7 \pm \sqrt{145}}{4}$

Ejercicio$\PageIndex{28}$

El producto de dos enteros impares consecutivos es 143. ¿Qué son?

Contestar: 11 y 13 o −11 y −13

Ejercicio$\PageIndex{29}$

Un estudio de la calidad del aire realizado por un grupo ambiental sugiere que dentro de t años el nivel de monóxido de carbono en el aire, en partes por millón, estará dado por la ecuación cuadrática

$A = 0.4t^2 + 0.1t + 3.1$

donde$A$ representa la cantidad de monóxido de carbono en el aire.

a) ¿Cuál es el nivel, en partes por millón, de monóxido de carbono en el aire ahora?

b) ¿Cuántos años a partir de ahora estará el nivel de monóxido de carbono en 18.1 partes por millón?

Contestar

a) 3.1

b) dentro de 6 años

Ejercicio$\PageIndex{30}$

El largo de un rectángulo es 6 pulgadas más largo que el ancho del rectángulo. Encuentra las dimensiones del rectángulo si el área es de 112 pies cuadrados.

Contestar

ancho:$\dfrac{-1 + \sqrt{1793}}{4}$

longitud:$\dfrac{1 + \sqrt{1793}}{4}$

Para los siguientes problemas, construya las gráficas de las siguientes ecuaciones.

Ejercicio$\PageIndex{31}$

$y = x^2 - 3$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

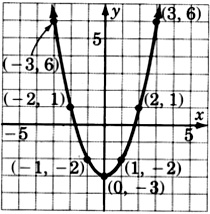
Contestar: $Gráfico de una parábola que pasa por siete puntos con coordenadas negativas tres, seis; negativas dos, uno; negativo uno, negativo dos; cero, negativo tres; uno, negativo dos; dos, uno; y tres, seis.$

Ejercicio$\PageIndex{32}$

$y = (x + 1)^2$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

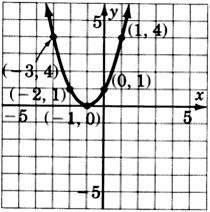
Contestar: $Gráfica de una parábola que pasa por cinco puntos con coordenadas negativas tres, cuatro; negativo dos, uno; negativo uno, cero; cero, uno; y uno, cuatro.$

Ejercicio$\PageIndex{33}$

$y = (x-2)^2 + 3$

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de una unidad en ambos ejes.$

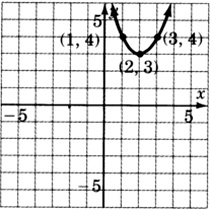
Contestar: $Gráfica de una parábola que pasa por tres puntos con las coordenadas uno, cuatro; dos, tres; y tres, cuatro.$

Para los siguientes problemas, escriba la ecuación que corresponda a cada gráfica.

Ejercicio$\PageIndex{34}$

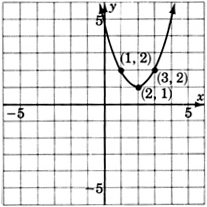
$Gráfica de una ecuación cuadrática que pasa por tres puntos con las coordenadas uno, dos; dos, uno; y tres, dos.$

Contestar: $y = (x-2)^2 + 1$o$y = x^2 - 4x + 5$

Ejercicio$\PageIndex{35}$

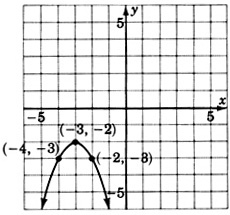
$Gráfica de una ecuación cuadrática que pasa por tres puntos con coordenadas negativas cuatro, negativas tres; negativas tres, negativas dos; y negativas dos, negativas tres.$

Contestar: $y = -(x + 3)^2 - 2$o$y = -x^2 - 6x - 11$

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Ejercicio\(\PageIndex{21}\)

Ejercicio\(\PageIndex{22}\)

Ejercicio\(\PageIndex{23}\)

Ejercicio\(\PageIndex{24}\)

Ejercicio\(\PageIndex{25}\)

Ejercicio\(\PageIndex{26}\)

Ejercicio\(\PageIndex{27}\)

Ejercicio\(\PageIndex{28}\)

Ejercicio\(\PageIndex{29}\)

Ejercicio\(\PageIndex{30}\)

Ejercicio\(\PageIndex{31}\)

Ejercicio\(\PageIndex{32}\)

Ejercicio\(\PageIndex{33}\)

Ejercicio\(\PageIndex{34}\)

Ejercicio\(\PageIndex{35}\)